ec6b0f6f00ca83528460492f03e60ab9.ppt
- Количество слайдов: 32
 ELEMENTARY DATA STRUCTURES Stacks, Queues, and Linked Lists
ELEMENTARY DATA STRUCTURES Stacks, Queues, and Linked Lists
 Elementary Data Structures z. Used as programming tools (stacks & queues) - software (i. e. compilers) - used in the operations of a certain task z. Implemented in CPU instructions - hardware
Elementary Data Structures z. Used as programming tools (stacks & queues) - software (i. e. compilers) - used in the operations of a certain task z. Implemented in CPU instructions - hardware
 Stacks z. Definition Õcontainer of objects Õuses LIFO principle for object operations Õoperations are push and pop z. Sample uses : ÕInternet browsers ÕUndo / Redo feature
Stacks z. Definition Õcontainer of objects Õuses LIFO principle for object operations Õoperations are push and pop z. Sample uses : ÕInternet browsers ÕUndo / Redo feature
 Other Applications z. Parsing - check for matching parenthesis or brackets - aid for algorithms applied to complex data structures (traverse nodes of a tree and searching vertices of a graph)
Other Applications z. Parsing - check for matching parenthesis or brackets - aid for algorithms applied to complex data structures (traverse nodes of a tree and searching vertices of a graph)
 Basic Stack Operations z push(o) z pop() z Inserts object o onto top of stack Input: object Output: none z Removes the top object of stack and returns it to calling method Input: none Output: object
Basic Stack Operations z push(o) z pop() z Inserts object o onto top of stack Input: object Output: none z Removes the top object of stack and returns it to calling method Input: none Output: object
 Related Stack Operations z is. Empty() z is. Full() z Returns a boolean indicating if stack is empty. Input: none Output: boolean z Returns a boolean indicating if stack is full Input: none Output: boolean
Related Stack Operations z is. Empty() z is. Full() z Returns a boolean indicating if stack is empty. Input: none Output: boolean z Returns a boolean indicating if stack is full Input: none Output: boolean
 Other Stack Operations z size() : z top() z Returns the number of objects in stack. Input: none Output: integer z Returns the top object of the stack. Input: none Output: object
Other Stack Operations z size() : z top() z Returns the number of objects in stack. Input: none Output: integer z Returns the top object of the stack. Input: none Output: object
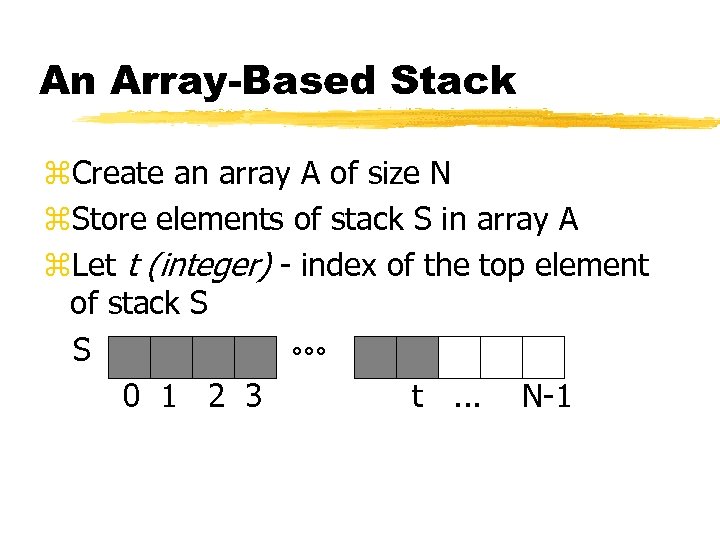 An Array-Based Stack z. Create an array A of size N z. Store elements of stack S in array A z. Let t (integer) - index of the top element of stack S S 0 1 2 3 t. . . N-1
An Array-Based Stack z. Create an array A of size N z. Store elements of stack S in array A z. Let t (integer) - index of the top element of stack S S 0 1 2 3 t. . . N-1
 Array Implementation z Algorithm size() return t + 1 z Algorithm isempty() return (t<0) z Algorithm push(o) if size()=N then throw a STACKEMPTYEXCEPTION t=t+1 S[t]=o
Array Implementation z Algorithm size() return t + 1 z Algorithm isempty() return (t<0) z Algorithm push(o) if size()=N then throw a STACKEMPTYEXCEPTION t=t+1 S[t]=o
![Array Implementation z Algorithm pop() if isempty() then throw a STACKEMPTYEXCEPTION e=S[t]=null t=t-1 return Array Implementation z Algorithm pop() if isempty() then throw a STACKEMPTYEXCEPTION e=S[t]=null t=t-1 return](https://present5.com/presentation/ec6b0f6f00ca83528460492f03e60ab9/image-10.jpg) Array Implementation z Algorithm pop() if isempty() then throw a STACKEMPTYEXCEPTION e=S[t]=null t=t-1 return e z Algorithm top() if isempty() then throw a STACKEMPTYEXCEPTION return S[t]
Array Implementation z Algorithm pop() if isempty() then throw a STACKEMPTYEXCEPTION e=S[t]=null t=t-1 return e z Algorithm top() if isempty() then throw a STACKEMPTYEXCEPTION return S[t]
 Class Problem z. Using the stack functions, make an algorithm that will determine that given a string x : a) has matching operands (i. e. (), {}, []) b) report an error if an operand is missing z. Example : x = “(12 xxs 3 e)”, correct x = “(sdfsdfs}”, error
Class Problem z. Using the stack functions, make an algorithm that will determine that given a string x : a) has matching operands (i. e. (), {}, []) b) report an error if an operand is missing z. Example : x = “(12 xxs 3 e)”, correct x = “(sdfsdfs}”, error
 Class Problem - Summary 1. 2. 3. 4. Make an empty stack Read characters until end of file If the character is an open anything, push it in the stack If it’s a close anything, then if stack is empty, report an error, otherwise, pop the stack 5. If popped symbol is not the corresponding opening symbol, then report an error 6. At end of file, if stack is not empty report an error
Class Problem - Summary 1. 2. 3. 4. Make an empty stack Read characters until end of file If the character is an open anything, push it in the stack If it’s a close anything, then if stack is empty, report an error, otherwise, pop the stack 5. If popped symbol is not the corresponding opening symbol, then report an error 6. At end of file, if stack is not empty report an error
 Stacks- other applications z. Recursion - i. e. computing for N factorial z. Operand parsing - evaluating an expression - i. e. ((4*5)+(6+2)/5)) - postfix notation A*B+C = AB*C+ zfunction calls - variables and routine position are saved
Stacks- other applications z. Recursion - i. e. computing for N factorial z. Operand parsing - evaluating an expression - i. e. ((4*5)+(6+2)/5)) - postfix notation A*B+C = AB*C+ zfunction calls - variables and routine position are saved
 Stacks - Query z. How can the undo/redo function be implemented using stacks ?
Stacks - Query z. How can the undo/redo function be implemented using stacks ?
 QUEUES z A queue is a container of objects that are inserted and removed according to the FIFO principle. z Operations: Enqueue - insert an item at the rear of queue z Dequeue - remove an item from the front of the queue z Sample uses : movie line printing queue
QUEUES z A queue is a container of objects that are inserted and removed according to the FIFO principle. z Operations: Enqueue - insert an item at the rear of queue z Dequeue - remove an item from the front of the queue z Sample uses : movie line printing queue
 The Queue Abstract Data Type z enqueue(o) z dequeue() z Insert object o at the rear of the queue Input: object Output: none z Remove the object from the front of the queue and return it. Input: none Output: object
The Queue Abstract Data Type z enqueue(o) z dequeue() z Insert object o at the rear of the queue Input: object Output: none z Remove the object from the front of the queue and return it. Input: none Output: object
 The Queue Abstract Data Type zsize() : Returns the number of objects in the queue. Input: none Output: object zis. Empty(): Return a boolean indicating if the queue is empty. Input: none Output: boolean zfront(): Return the front object of the queue.
The Queue Abstract Data Type zsize() : Returns the number of objects in the queue. Input: none Output: object zis. Empty(): Return a boolean indicating if the queue is empty. Input: none Output: boolean zfront(): Return the front object of the queue.
 Array Implementation z. Create a queue using an array in a circular fashion z. Queue consists of an N-element array Q and two integer variables: f : index of the front element r: index of the element after the rear one z. Configurations : “normal” “wrapped around”
Array Implementation z. Create a queue using an array in a circular fashion z. Queue consists of an N-element array Q and two integer variables: f : index of the front element r: index of the element after the rear one z. Configurations : “normal” “wrapped around”
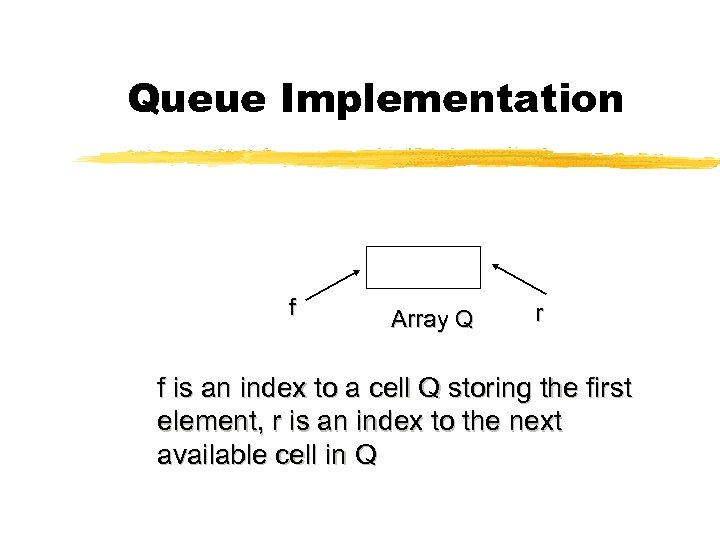 Queue Implementation f Array Q r f is an index to a cell Q storing the first element, r is an index to the next available cell in Q
Queue Implementation f Array Q r f is an index to a cell Q storing the first element, r is an index to the next available cell in Q
 Queues- Example z. Print Jobs - All requests from workstations are enqueued to the print queue on a first come first served basis - The current (first) printjob is dequeued and sent to the printer for processing
Queues- Example z. Print Jobs - All requests from workstations are enqueued to the print queue on a first come first served basis - The current (first) printjob is dequeued and sent to the printer for processing
 Queue - Applications z. I/O Request Handling File server - Workstation (print, data access, etc. ) z. Telephone Call Handling z. History functions in applications
Queue - Applications z. I/O Request Handling File server - Workstation (print, data access, etc. ) z. Telephone Call Handling z. History functions in applications
 Limitations - Using Arrays z. Maximum size needs to be predetermined z. Potential wastage of allocated memory z. Need to handle overflow
Limitations - Using Arrays z. Maximum size needs to be predetermined z. Potential wastage of allocated memory z. Need to handle overflow
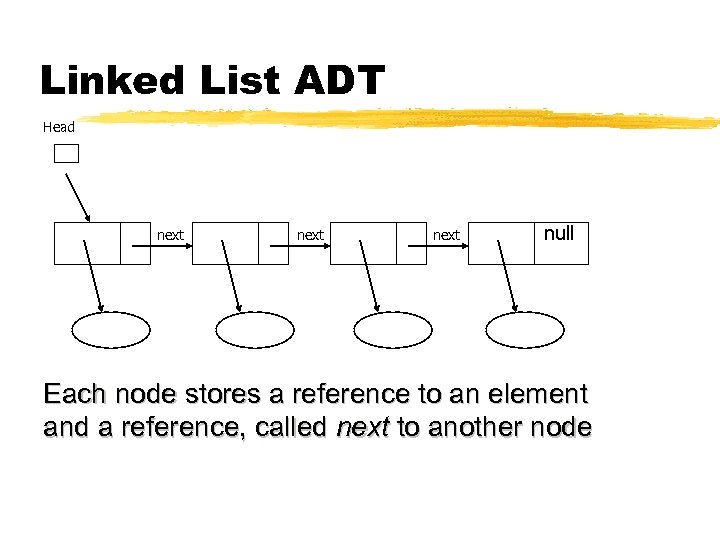 Linked List ADT Head next null Each node stores a reference to an element and a reference, called next to another node
Linked List ADT Head next null Each node stores a reference to an element and a reference, called next to another node
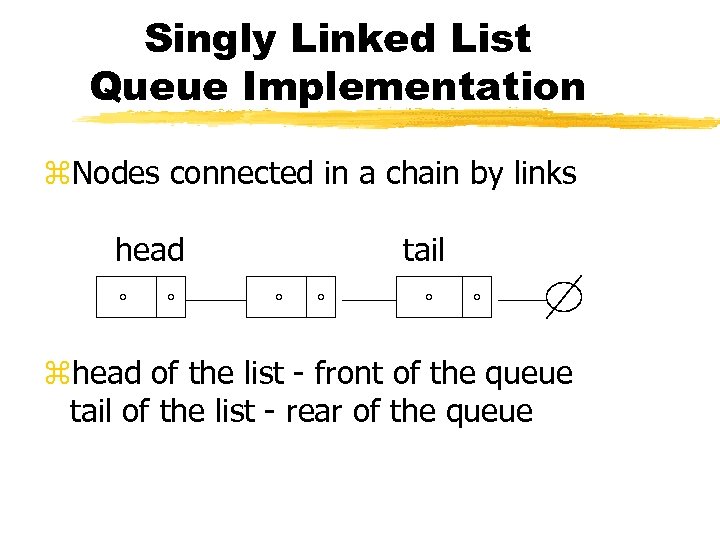 Singly Linked List Queue Implementation z. Nodes connected in a chain by links head tail zhead of the list - front of the queue tail of the list - rear of the queue
Singly Linked List Queue Implementation z. Nodes connected in a chain by links head tail zhead of the list - front of the queue tail of the list - rear of the queue
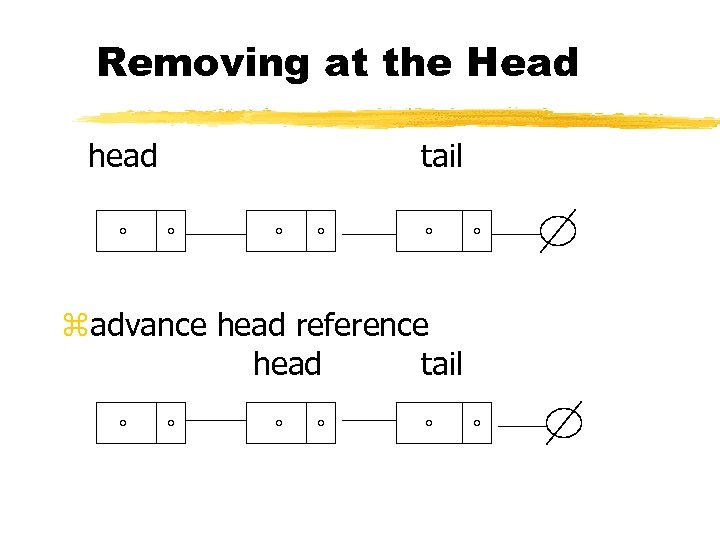 Removing at the Head head tail zadvance head reference head tail
Removing at the Head head tail zadvance head reference head tail
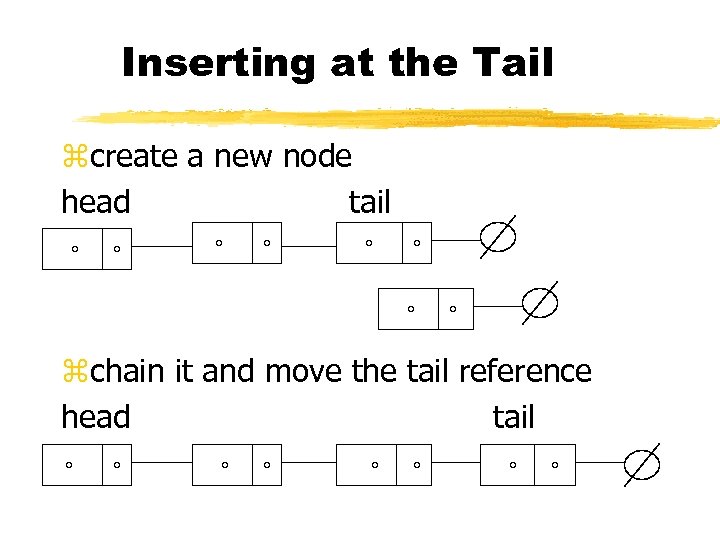 Inserting at the Tail zcreate a new node head tail zchain it and move the tail reference head tail
Inserting at the Tail zcreate a new node head tail zchain it and move the tail reference head tail
 Other Advantages z. Insertions and deletions are easier compared to an array implementation when dealing with “lists”
Other Advantages z. Insertions and deletions are easier compared to an array implementation when dealing with “lists”
 Linked Lists - Query z. If a stack will be implemented using a linked list, is it better to assign the head or the tail as the top of the stack ? Why ?
Linked Lists - Query z. If a stack will be implemented using a linked list, is it better to assign the head or the tail as the top of the stack ? Why ?
 Double-Ended Queues z. Data structure that allows insertion and deletion at the front and the rear end of the queue (pronounced as “deck”)
Double-Ended Queues z. Data structure that allows insertion and deletion at the front and the rear end of the queue (pronounced as “deck”)
 Doubly linked lists z. A node in a doubly linked list is like a node in a singly linked list except that, in addition to the next link, it also has a prev link to the previous node in the list. z. Advantage over singly linked lists : deletions at the tail of the list can be done in constant time
Doubly linked lists z. A node in a doubly linked list is like a node in a singly linked list except that, in addition to the next link, it also has a prev link to the previous node in the list. z. Advantage over singly linked lists : deletions at the tail of the list can be done in constant time
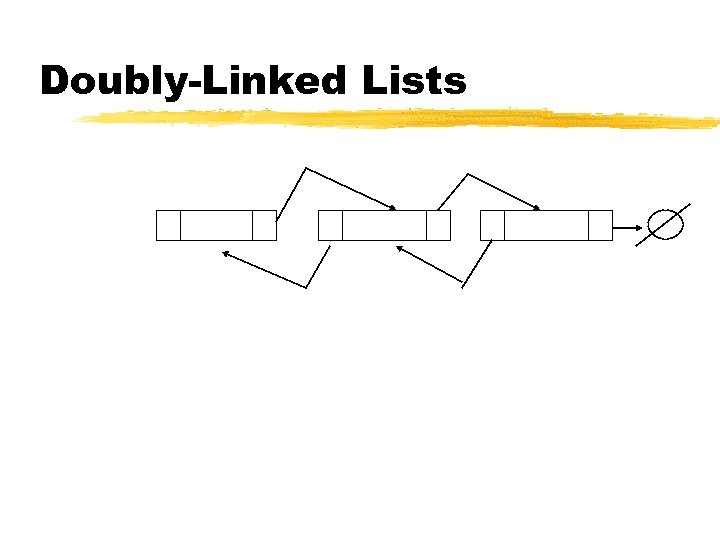 Doubly-Linked Lists
Doubly-Linked Lists
 Linked Lists - Query z. What is the running time to search for an entry in a linked list ? Deleting from the tail ? Inserting from the head ?
Linked Lists - Query z. What is the running time to search for an entry in a linked list ? Deleting from the tail ? Inserting from the head ?


