ЕЛЕКТРОТЕХНІКА Лекція 4 Не розгалуджені кола змінного струму

ЕЛЕКТРОТЕХНІКА Лекція 4. Не розгалуджені кола змінного струму

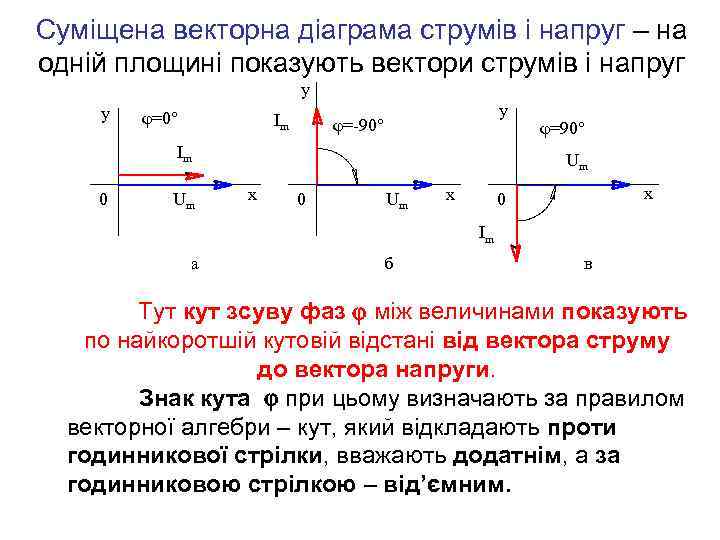Суміщена векторна діаграма струмів і напруг – на одній площині показують вектори струмів і напруг y y φ=0° Im y φ=-90° Im 0 Um φ=90° Um x 0 Um x x 0 Im a б в Тут кут зсуву фаз між величинами показують по найкоротшій кутовій відстані від вектора струму до вектора напруги. Знак кута при цьому визначають за правилом векторної алгебри – кут, який відкладають проти годинникової стрілки, вважають додатнім, а за годинниковою стрілкою – від’ємним.

Діюче значення синусоїдного струму Широке впровадження синусоїдного струму обумовило необхідність пошуку простого та зручного способу визначення енергії, що віддає струм до зовнішнього кола. Згідно закону Джоуля-Ленца при проходженні постійного струму І по провіднику з опором R, за час t виділяється кількість теплоти: або За період T (t =Т), с, : При цьому електрична потужність, як робота струму в одиницю часу, або інтенсивність нагрівання: Кількість теплоти, яка виділиться при проходженні змінного струму –

Отже, змінним струмом за той же час Т в тому ж опорі R буде виділено теплоти: Оскільки то:

Отже, під діючим значенням змінного струму розуміють таке значення еквівалентного йому постійного струму, який проходячи в тому ж, що і змінний струм провіднику, за однаковий час виділяє у цьому провіднику таку ж кількість теплоти. Іншими словами можна сказати, що це є такий змінний струм, який за своєю роботою (дією) є адекватний роботі постійного струму. Використавши, що ; і що Відношення амплітудного значення змінної електричної величини до її діючого значення називають коефіцієнтом амплітуди: kа = Im / I = 1, 41

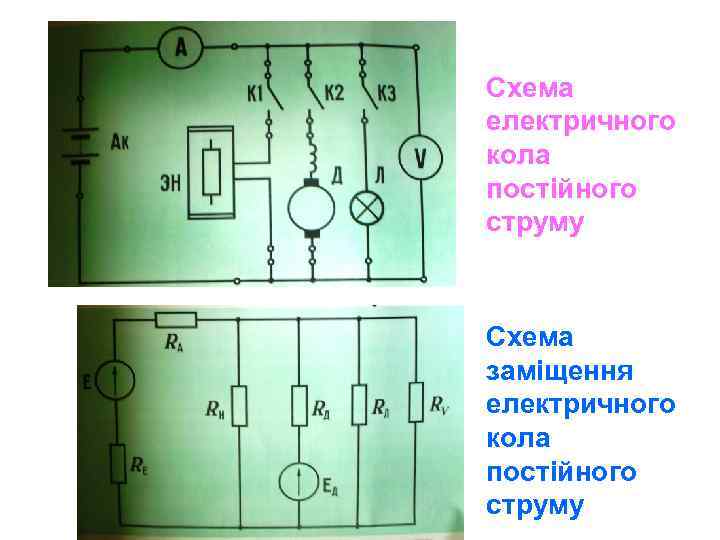Схема електричного кола постійного струму Схема заміщення електричного кола постійного струму

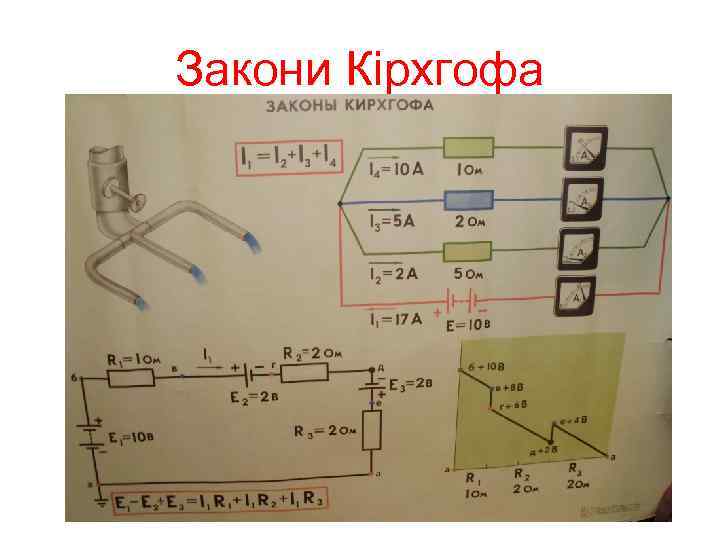Закони Кірхгофа

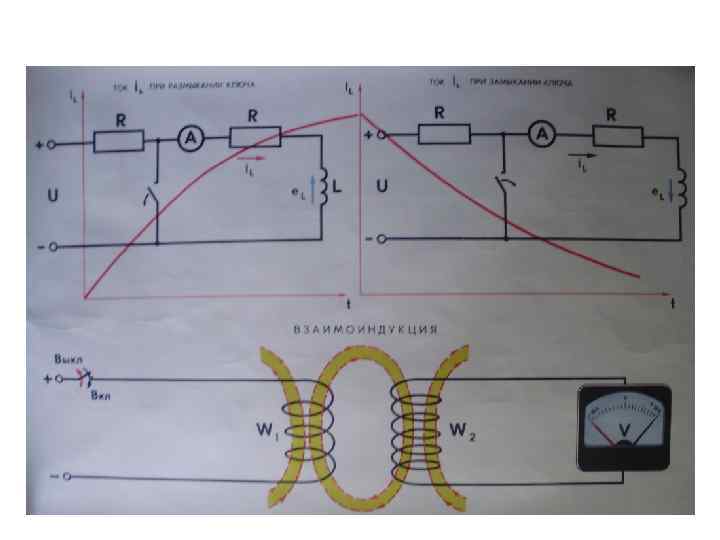
Нерозгалужені електричні кола змінного струму Коло синусоїдного струму з резистором. Електричні кола, до складу яких входять лампи розжарювання, нагрівальні прилади, реостати, а також з’єднувальні провідники, за властивостями наближаються до таких, що мають тільки активний опір. При виконанні інженерних розрахунків електричних кіл реактивними опорами вказаних споживачів здебільшого нехтують. Стосовно джерела змінного струму ці пристрої називають активним або резистивним навантаженням. Вид кола з резистором, до якого підведена напруга Оскільки внутрішній опор провідників дуже малий, то i згідно з другим законом Кірхгофа спад напруги ua на u ua r резисторі буде дорівнювати прикладеній напрузі:

При r = const максимальному миттєвому значенню напруги відповідає максимальне значення струму Iam = Uam/r, рівняння розрахунку струму кола згідно закону Ома: або – Поділивши обидві частини рівняння Im = Um/r на Висновки: 1. Струм кола, яке містить тільки активний опір, змінюється за тим же законом (у даному випадку синусоїдним) і з тією ж частотою, що і прикладена до кола напруга. 2. Оскільки в рівняннях, що описують синусоїди струму і напруги кола (ділянки кола) з резистором, фазові кути дорівнюють один одному ( t + i = t + u), то ці синусоїди співпадають між собою за фазою, отже, кут зсуву фаз між ними дорівнює нулю ( φ = u i = 0 ).

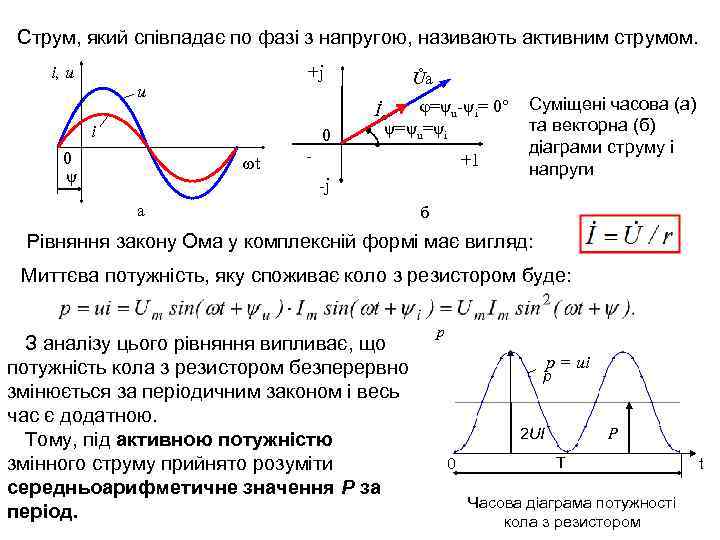Струм, який співпадає по фазі з напругою, називають активним струмом. i, u +j u i 0 0 ψ t Ůa φ=ψu-ψi= 0° İа ψ=ψu=ψi - +1 -j а Суміщені часова (а) та векторна (б) діаграми струму і напруги б Рівняння закону Ома у комплексній формі має вигляд: Миттєва потужність, яку споживає коло з резистором буде: З аналізу цього рівняння випливає, що потужність кола з резистором безперервно змінюється за періодичним законом і весь час є додатною. Тому, під активною потужністю змінного струму прийнято розуміти середньоарифметичне значення P за період. р p = ui p 2 UI 0 P T Часова діаграма потужності кола з резистором t

Тобто, для визначення активної потужності споживача достатньо енергію W, що витрачається струмом протягом періоду, поділити на тривалість періоду – Додатній знак у функції p від t означає, що при проходженні змінного струму активний елемент завжди споживає електричну енергію джерела. При цьому електрична енергія незворотно перетворюється у теплову – активний опір нагрівається. Потужність, яку у колах змінного струму споживає резистор, називають активною і вимірюють у ватах (1 Вт=1 Дж/1 с). Активна потужність джерела:

Коло синусоїдного струму з ємністю Коло, яке стосовно джерела синусоїдної напруги u = UСmsin( t u) має i виключно ємнісний характер навантаження u C u. C можна надати у вигляді конденсатора ємністю С, що підключений до джерела дуже короткими провідниками, опором яких можна знехтувати: Струм у такому колі являє собою рух зарядів q до обкладинок конденсатора і може бути описаний диференційним рівнянням – де u. С – спад напруги на конденсатор Враховуючі, що внутрішній опір з’єднувальних проводів дуже малий і, отже, згідно з другим законом Кірхгофа –

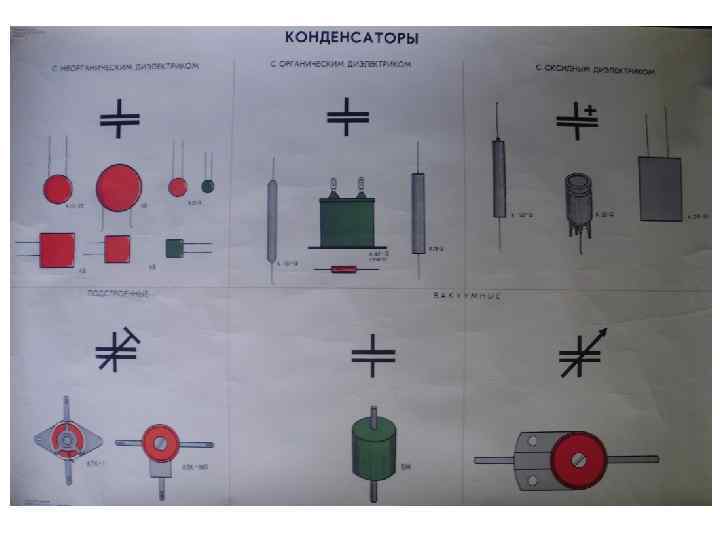
рішення диференційного рівняння буде мати вигляд: Розділивши обидві частини виразу значення струму ємності (Im = CUm) на одержимо рівняння розрахунку діючого струму кола – закон Ома для кола (ділянки) з ємністю: амплітудного де x. C = 1/( C) = 1/(2 f. C) – реактивний опір ємності, або ємнісний опір, який відображає вплив ємності на величину діючого струму. Для кола (ділянки кола) з ємністю закон Ома у комплексній формі:

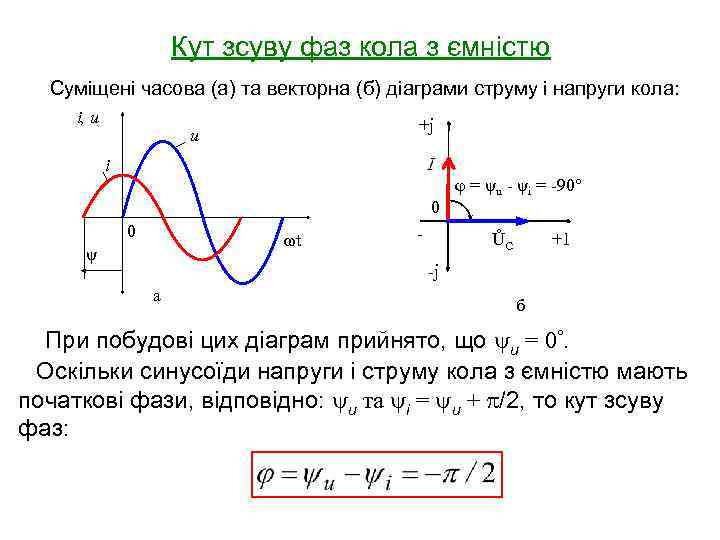Кут зсуву фаз кола з ємністю Суміщені часова (а) та векторна (б) діаграми струму і напруги кола: i, u +j u i 0 0 ωt ψ - φ = ψu - ψi = -90° +1 ŮC -j а б При побудові цих діаграм прийнято, що u = 0. Оскільки синусоїди напруги і струму кола з ємністю мають початкові фази, відповідно: u та i = u + /2, то кут зсуву фаз:

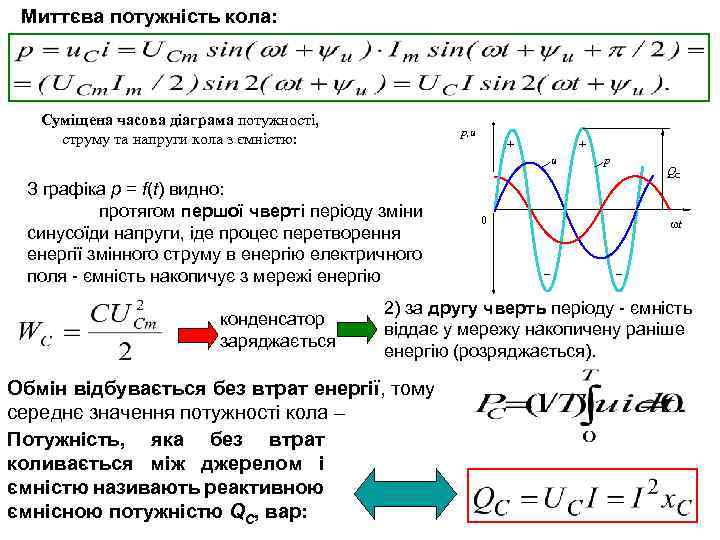Миттєва потужність кола: Суміщена часова діаграма потужності, струму та напруги кола з ємністю: p, u + + u З графіка p = f(t) видно: протягом першої чверті періоду зміни синусоїди напруги, іде процес перетворення енергії змінного струму в енергію електричного поля - ємність накопичує з мережі енергію конденсатор заряджається p QC 0 t – – 2) за другу чверть періоду - ємність віддає у мережу накопичену раніше енергію (розряджається). Обмін відбувається без втрат енергії, тому середнє значення потужності кола – Потужність, яка без втрат коливається між джерелом і ємністю називають реактивною ємнісною потужністю QC, вар:

Коло синусоїдного струму з індуктивністю u Розглянемо електричне коло, в якому індуктивність L підключена до джерела синусоїдного струму: Коло, яке по відношенню до джерела змінного струму i має практично індуктивний характер навантаження можна надати у вигляді котушки, що виконана з мідного проводу великого перерізу. Активний опір витків проводу u L у такої котушки буде дуже малий і на практиці його величиною можна знехтувати. Котушку, активний опір витків якої нескінченно малий називають індуктивністю або ідеальною котушкою. При проходженні синусоїдного струму в витках котушки генерується ЕРС самоіндукції – яка за величиною дорівнює напрузі u. L, але має протилежний напрямок, тобто u. L = e L

Коло з індуктивністю. Закон Ома Підставимо значення i у вираз ЕРС і, після диференціювання, одержимо рівняння розрахунку спаду напруги на індуктивності: де ULm = LIm розділивши UL = LI Після перетворень - одержимо закон Ома у діючих значеннях: де x. L = 2 f. L – реактивний опір індуктивності (індуктивний опір), який враховує реакцію кола на зміну магнітного потоку в індуктивності. Закон Ома у комплексній формі

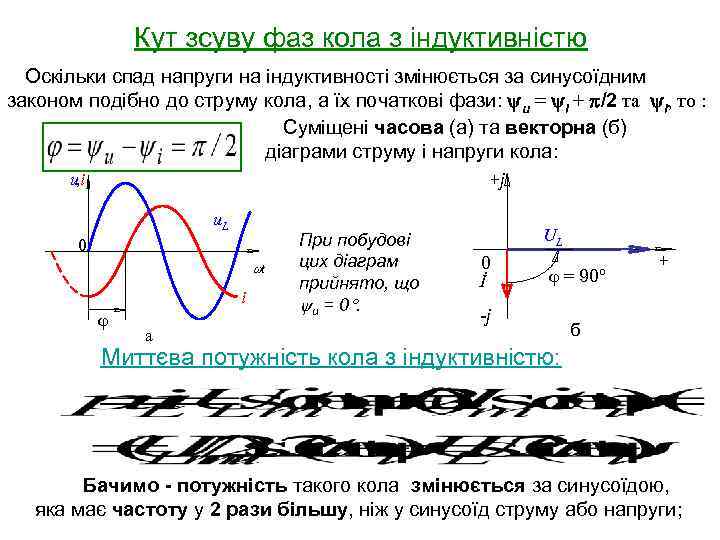Кут зсуву фаз кола з індуктивністю Оскільки спад напруги на індуктивності змінюється за синусоїдним законом подібно до струму кола, а їх початкові фази: u = i + /2 та i, то : Суміщені часова (а) та векторна (б) діаграми струму і напруги кола: +j u, i u. L 0 wt i j а При побудові цих діаграм прийнято, що u = 0 . UL 0 İ j = 90º -j + б Миттєва потужність кола з індуктивністю: Бачимо - потужність такого кола змінюється за синусоїдою, яка має частоту у 2 рази більшу, ніж у синусоїд струму або напруги;

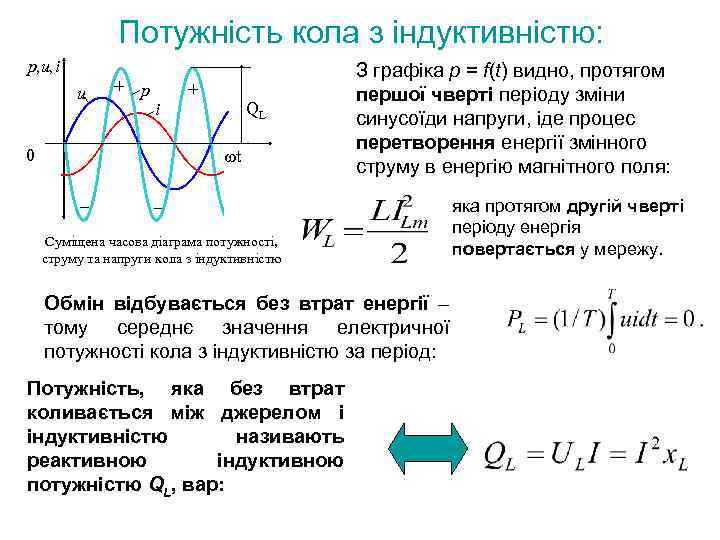Потужність кола з індуктивністю: p, u, i u + p + QL i t 0 – З графіка p = f(t) видно, протягом першої чверті періоду зміни синусоїди напруги, іде процес перетворення енергії змінного струму в енергію магнітного поля: – Суміщена часова діаграма потужності, струму та напруги кола з індуктивністю Обмін відбувається без втрат енергії – тому середнє значення електричної потужності кола з індуктивністю за період: Потужність, яка без втрат коливається між джерелом і індуктивністю називають реактивною індуктивною потужністю QL, вар: яка протягом другій чверті періоду енергія повертається у мережу.

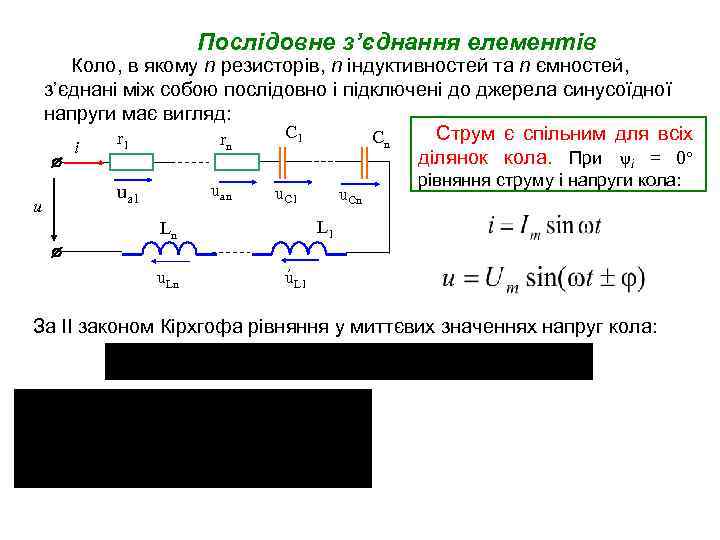Послідовне з’єднання елементів Коло, в якому n резисторів, n індуктивностей та n ємностей, з’єднані між собою послідовно і підключені до джерела синусоїдної напруги має вигляд: C 1 Струм є спільним для всіх Cn r 1 rn i ділянок кола. При i = 0 u uan ua 1 u. C 1 рівняння струму і напруги кола: L 1 Ln u. Cn , u. L 1 За ІІ законом Кірхгофа рівняння у миттєвих значеннях напруг кола:

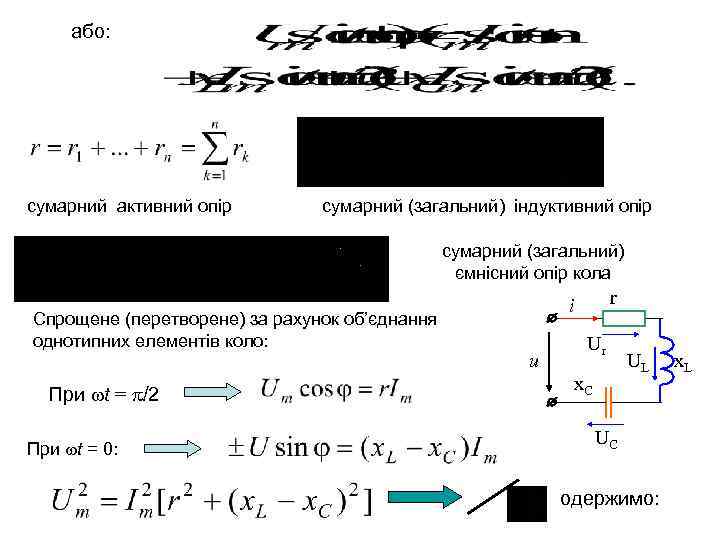або: сумарний активний опір сумарний (загальний) індуктивний опір сумарний (загальний) ємнісний опір кола Спрощене (перетворене) за рахунок об’єднання однотипних елементів коло: При t = /2 При t = 0: r i u Ur х. C UL UC одержимо: х. L

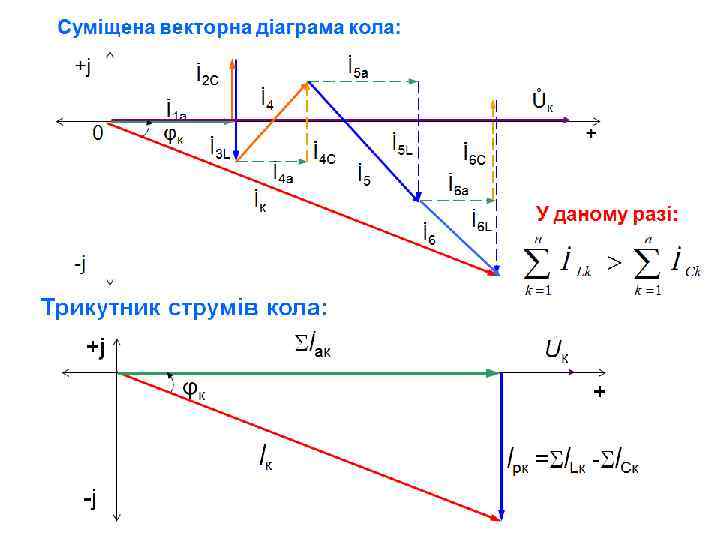
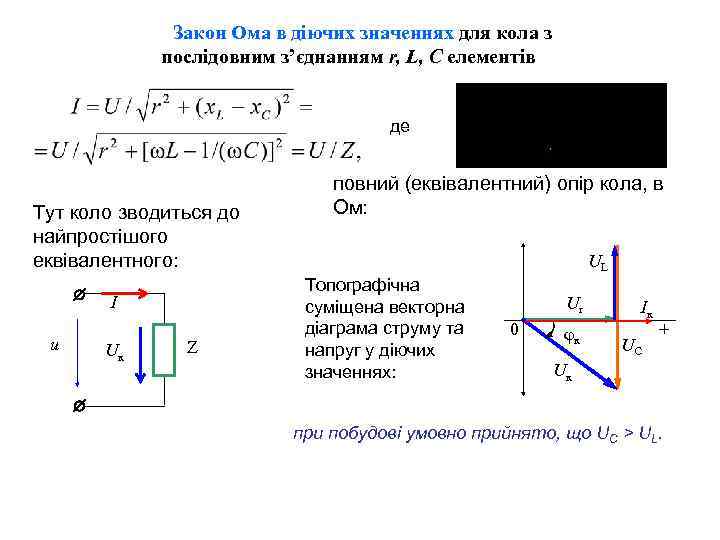Закон Ома в діючих значеннях для кола з послідовним з’єднанням r, L, C елементів де Тут коло зводиться до найпростішого еквівалентного: І u Uк Z повний (еквівалентний) опір кола, в Ом: UL Топографічна суміщена векторна діаграма струму та напруг у діючих значеннях: Ur 0 φк Ік UC + Uк при побудові умовно прийнято, що UC > UL.

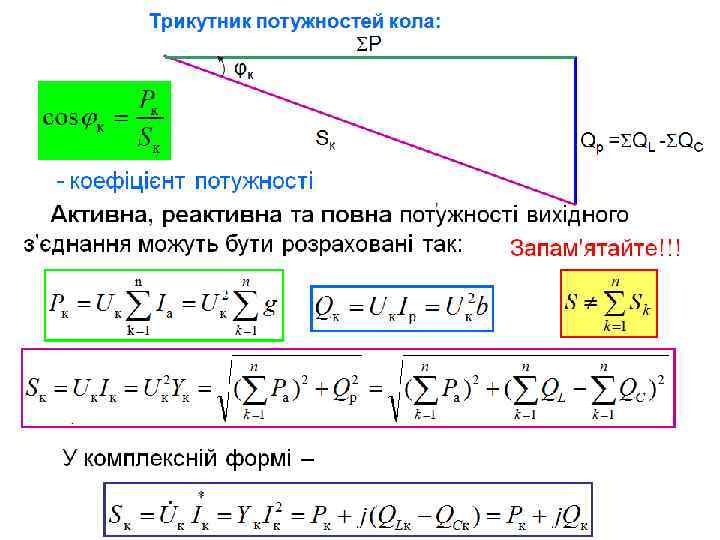
Закон Ома та потужність кола В результаті ділення кожної із сторін трикутника напруг на струм кола отримуємо трикутник опорів В результаті множення кожної зі сторін трикутника напруг на струм кола отримуємо трикутник потужностей P r φк Zк φк jx = j(x. L-x. C) Sк j. Q = j(QL-QC)

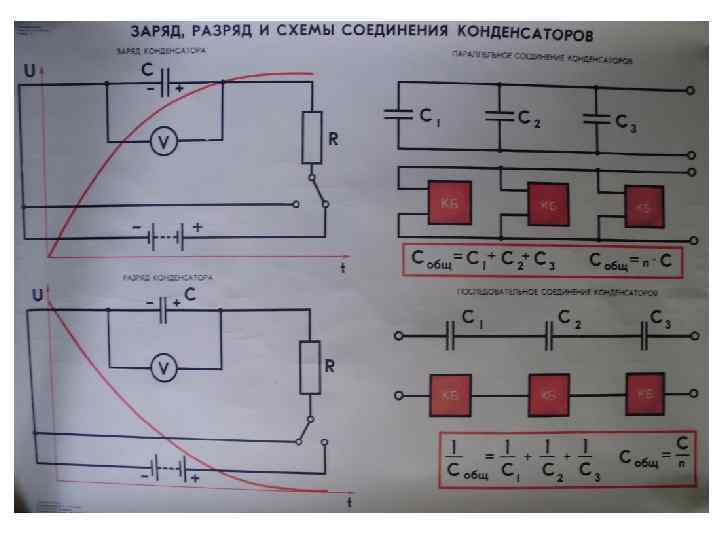
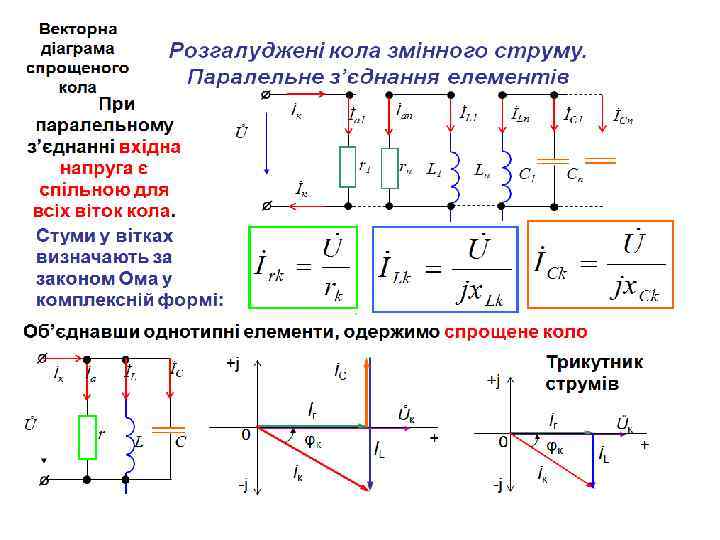
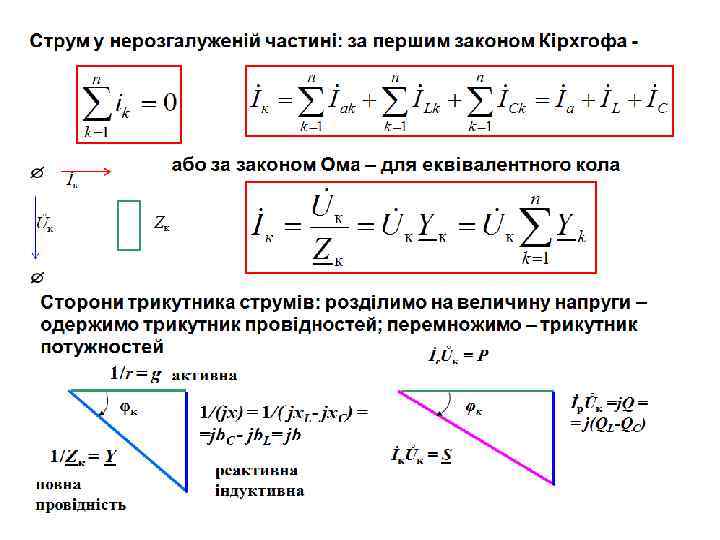
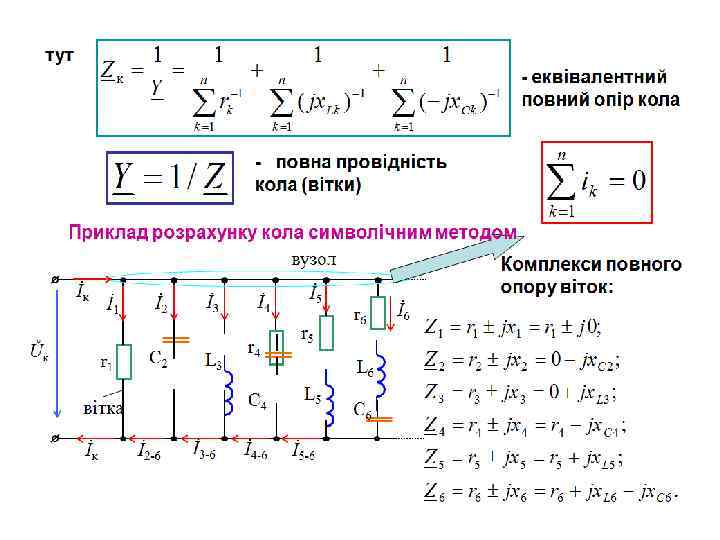
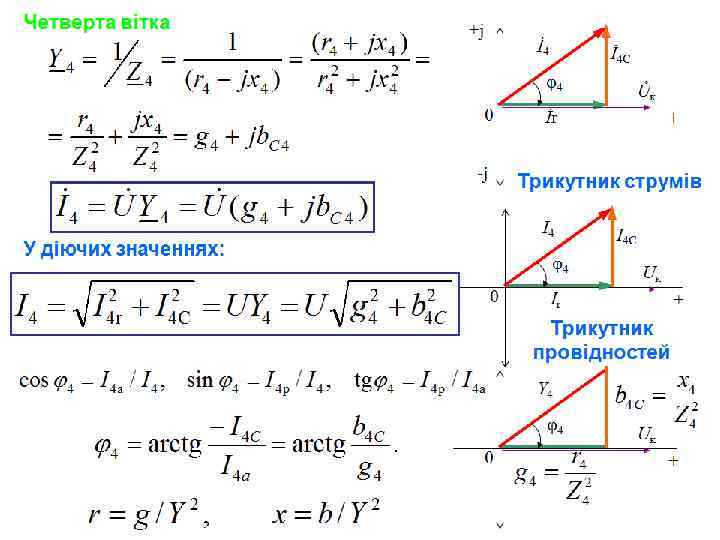
П'ята вітка +j İ 5 a 0 φ5 Ůк + İ 5 L İ 5 -j Трикутник струмів I 5 r У діючих значеннях: 0 φ5 Uк I 5 L İ 5 φ5 Y 5 Трикутник провідностей +

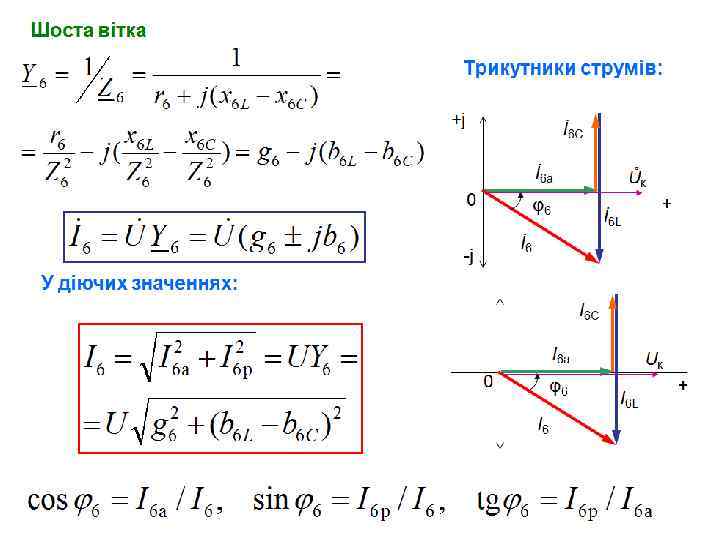
Трикутник провідностей Як бачимо, на відміну від кіл постійного струму, де є тільки один вид провідності, у колах змінного струму мають місце повна Y, активна g і реактивна b = b. C b. L, (індуктивна – b. L або ємнісна – b. С) провідності. Їх, як і провідність у колах постійного струму, вимірюють у сименсах, 1 См = 1 Ом 1. 0 φ6 Y 6 +