Электростатическое поле — вызвано присутствием неподвижных зарядов

Электростатическое поле -- вызвано присутствием неподвижных зарядов

1. Электростатическое поле в вакууме 1. 1 Электрический заряд и его свойства Существуют заряды двух типов – положительные и отрицательные. Свойства зарядов: 1) Электрический заряд любого типа состоит из целого числа элементарных зарядов Под элементарным отрицательным зарядом понимают заряд электрона, под элементарным положительным зарядом – заряд протона. 2) Закон сохранения заряда. В электрически изолированной системе, независимо от природы происходящих в ней процессов, алгебраическая сумма зарядов есть величина постоянная. 3) Величина заряда не зависит от того, покоится заряженное тело или движется, она имеет одно и то же значение в различных инерциальных системах отсчета.

4) Заряженные тела взаимодействуют между собой Закон взаимодействия точечных зарядов (Закон Кулона ) формулируется следующим образом: Между двумя неподвижными точечными зарядами, находящимися в вакууме, существует сила взаимодействия , пропорциональная произведению этих зарядов и обратно пропорциональная квадрату расстояния между ними. Векторная форма закона Кулона имеет вид: где – сила, действующая на данный заряд со стороны другого, – вектор, проведенный к рассматриваемому заряду от другого заряда (рис. 1. 1). Скалярная форма закона Кулона в СИ имеет вид Рис. 1. 1

. Введем новые понятия. Точечный заряд – заряженное тело, формой и размерами которого можно пренебречь. Пробный заряд – положительный заряд, достаточно малый по величине, чтобы при внесении его во внешнее поле не изменять это поле. ( «пробный» заряд – фактически это «прибор» , которым мы «пробуем» , есть электрическое поле или нет). 1. 2 Напряженность электрического поля. Электрическое поле – область пространства, в каждой точке которого существует сила, действующая на электрический заряд, помещенный в эту точку. Поле, действие которого на помещенные в него заряды со временем не меняется, называется статическим. При помещении точечного пробного заряда в электрическое поле на него со стороны этого поля действует сила. Причем оказывается, что отношение этой силы от свойств пробного заряда к величине пробного заряда совершенно не зависит, а определяется только свойствами поля в данной точке. Поэтому этим отношением описывают силовую характеристику электрического поля и называют ее напряженностью. (1. 1)

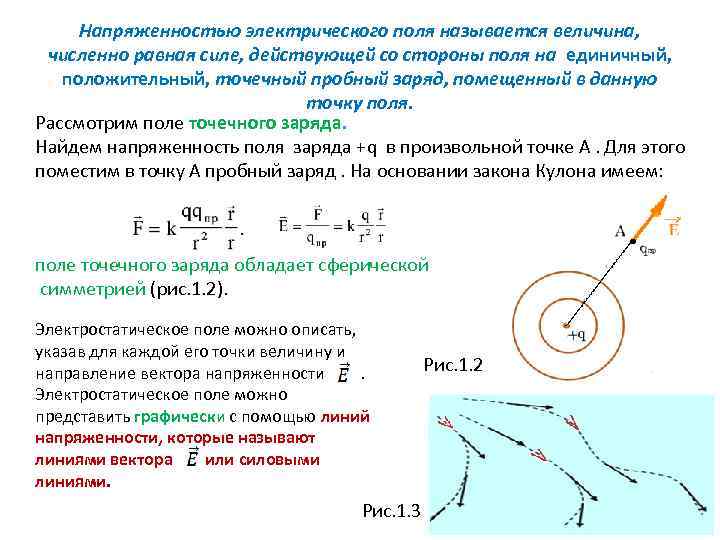Напряженностью электрического поля называется величина, численно равная силе, действующей со стороны поля на единичный, положительный, точечный пробный заряд, помещенный в данную точку поля. Рассмотрим поле точечного заряда. Найдем напряженность поля заряда +q в произвольной точке А. Для этого поместим в точку А пробный заряд. На основании закона Кулона имеем: поле точечного заряда обладает сферической симметрией (рис. 1. 2). Электростатическое поле можно описать, указав для каждой его точки величину и направление вектора напряженности. Электростатическое поле можно представить графически с помощью линий напряженности, которые называют линиями вектора или силовыми линиями. Рис. 1. 3 Рис. 1. 2

Линией напряженности называется такая линия, касательная в каждой точке которой совпадает по направлению с вектором напряженности в данной точке. Свойства линий напряженности: – начинаются у (+) q и оканчиваются у (-) q, или уходят на бесконечность; -- в каждой точке поля вектор имеет только одно направление, поэтому силовые линии нигде не пересекаются. – принято, чтобы количество линий напряженности, пересекающих единичную площадку, расположенную перпендикулярно линиям в окрестности данной точки, было пропорционально (или равно) в данной точке (см. рис. 1. 4). Рис. 1. 4 В последнем выражении коэффициент пропорциональности равен единице, так как речь идет о числовом равенстве, знак равенства заключен в скобки.

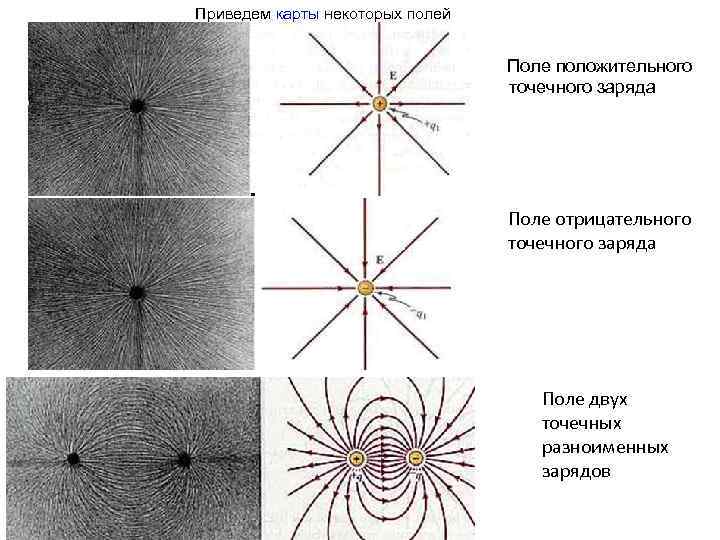Приведем карты некоторых полей Поле положительного точечного заряда Поле отрицательного точечного заряда Поле двух точечных разноименных зарядов

Важнейшие конфигурации полей – Центрально-симметричное поле – силовые линии направлены по радиальным линиям к центру или от центра. Это поле точечного заряда. –Однородное поле – вектор напряженности одинаков во всех точках поля по величине и направлению (рис. 1. 5 ). Такое поле изображается семейством параллельных прямых одинаковой густоты. 1. 3 Принцип суперпозиции электрических полей Рис. 1. 5 Он следует из принципа суперпозиции кулоновских сил. Опыт показывает: взаимодействие двух зарядов не зависит от присутствия третьего:

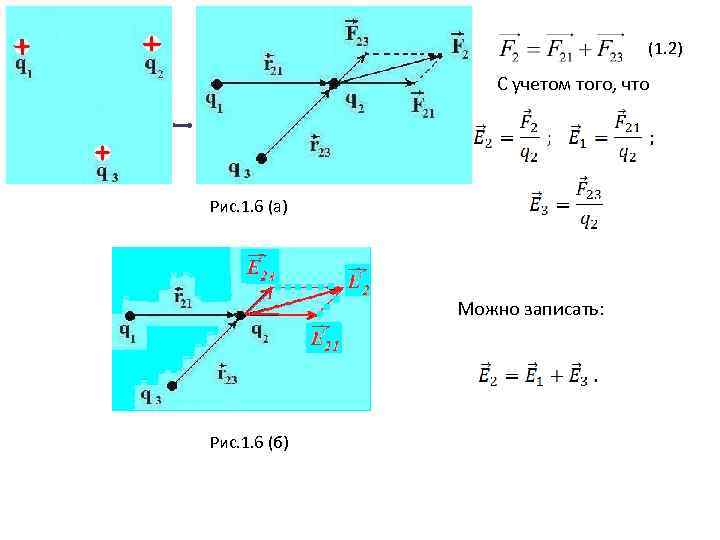(1. 2) С учетом того, что Рис. 1. 6 (а) Можно записать: Рис. 1. 6 (б)

В общем случае, если в пространстве расположена система зарядов то напряженность поля системы в произвольной точке: (1. 3) – математическое выражение принципа суперпозиции. Формулировка принципа суперпозиции: «Напряженность электростатического поля , создаваемого системой точечных зарядов в произвольной его точке равна векторной сумме напряженностей полей, создаваемых в этой точке каждым зарядом в отдельности» .

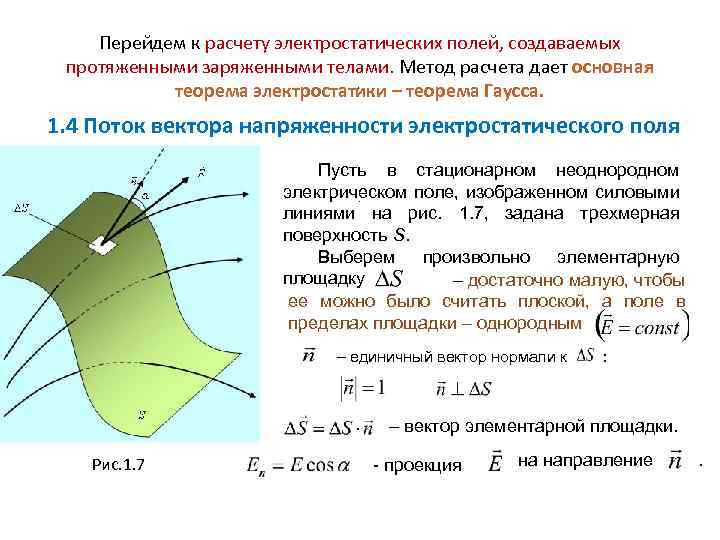Перейдем к расчету электростатических полей, создаваемых протяженными заряженными телами. Метод расчета дает основная , теорема электростатики – теорема Гаусса. 1. 4 Поток вектора напряженности электростатического поля Пусть в стационарном неоднородном электрическом поле, изображенном силовыми. линиями на рис. 1. 7, задана трехмерная поверхность S. Выберем произвольно элементарную площадку – достаточно малую, чтобы ее можно было считать плоской, а поле в пределах площадки – однородным – единичный вектор нормали к : – вектор элементарной площадки. Рис. 1. 7 - проекция на направление .

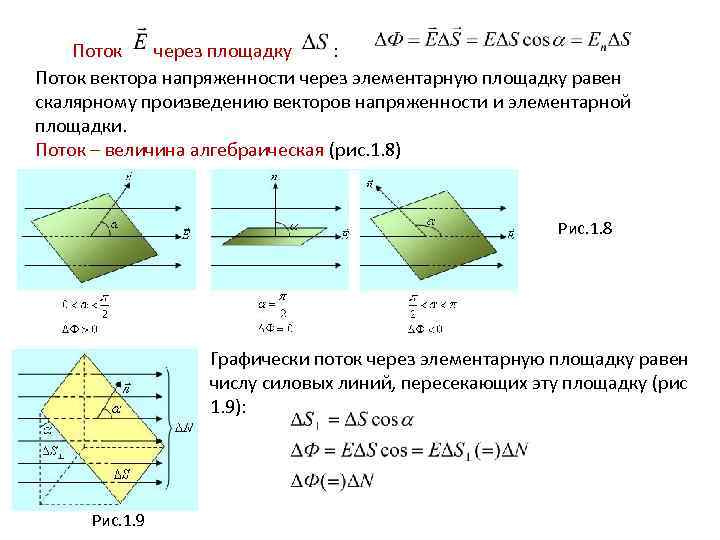Поток через площадку : Поток вектора напряженности через элементарную площадку равен скалярному произведению векторов напряженности и элементарной площадки. Поток – величина алгебраическая (рис. 1. 8) Рис. 1. 8 Графически поток через элементарную площадку равен числу силовых линий, пересекающих эту площадку (рис 1. 9): Рис. 1. 9

Условились: Все нормали к элементарным площадкам направлены по одну сторону от поверхности S. Нормали к замкнутой поверхности всегда направлены наружу. Полный поток Ф вектора через поверхность S (1. 4) Поток вектора напряженности поля через поверхность равен интегралу по этой поверхности от нормальной составляющей вектора к этой поверхности. Графически поток вектора через поверхность равен алгебраическому числу силовых линий, пересекающих поверхность. Вклад линий в поток положителен N+, если они направлены в ту же сторону от поверхности, что и нормаль, в противном случае их вклад в поток отрицателен N-. В случае замкнутой поверхности S число линий N+ вытекает, а N- втекает в нее (рис 1. 10) Пример: рис 1. 10

1. 5 Теорема Гаусса для вектора напряженности электростатического поля в вакууме Это основная теорема электростатики, позволяющая рассчитать созданных любыми протяженными заряженными телами. Формулировка интегральной формы теоремы: поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на электрическую постоянную . полей, (1. 5) Рассмотрим несколько соображений. 1. Проверим справедливость теоремы в поле точечного заряда (рис 1. 11). В силу симметрии поля на поверхности сферы S – совпадает с точечного заряда, , полученной из закона Кулона. Число силовых линий поля рис 1. 11

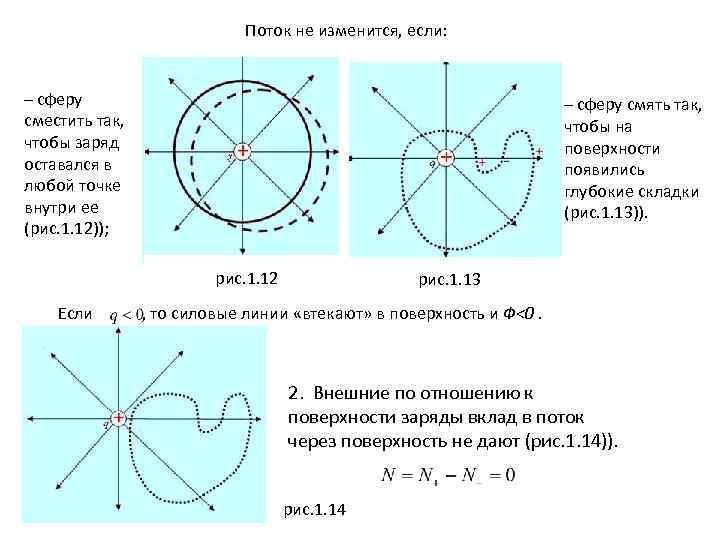Поток не изменится, если: – сферу сместить так, чтобы заряд оставался в любой точке внутри ее (рис. 1. 12)); – сферу смять так, чтобы на поверхности появились глубокие складки (рис. 1. 13)). рис. 1. 12 Если рис. 1. 13 , то силовые линии «втекают» в поверхность и Ф<0. 2. Внешние по отношению к поверхности заряды вклад в поток через поверхность не дают (рис. 1. 14)). рис. 1. 14

3. Если внутри поверхности находятся несколько зарядов Физический смысл теоремы Гаусса: Электростатическое поле имеет источники – (рис 1. 10) , где начинаются силовые линии, и стоки – (-)q, где силовые линии заканчиваются. Поток вектора через поверхность S характеризует мощность источников и стоков поля , находящихся внутри этой поверхности. Теорема Гаусса является обобщением опытного закона Кулона и принципа суперпозиции напряженностей полей. Она позволяет рассчитать поля , созданного протяженными заряженными телами. 1. 6 Применение теоремы Гаусса к расчету полей высокой симметрии. Порядок применения теоремы: 0. Установить геометрию поля. 1. Через точку наблюдения провести замкнутую поверхность S так, чтобы по возможности была перпендикулярна или параллельна S. 2. Рассчитать поток вектора через поверхность и заряд q внутри поверхности. 3. Полученные выражения подставить в теорему Гаусса и вывести формулу для в точке наблюдения.

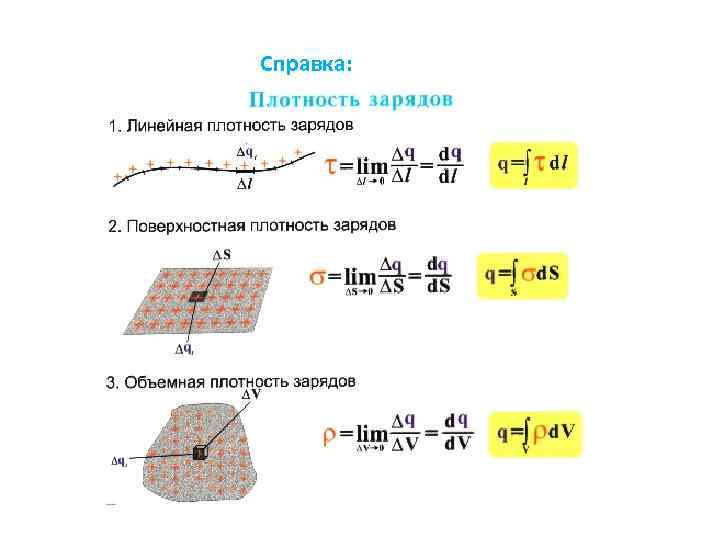Справка:

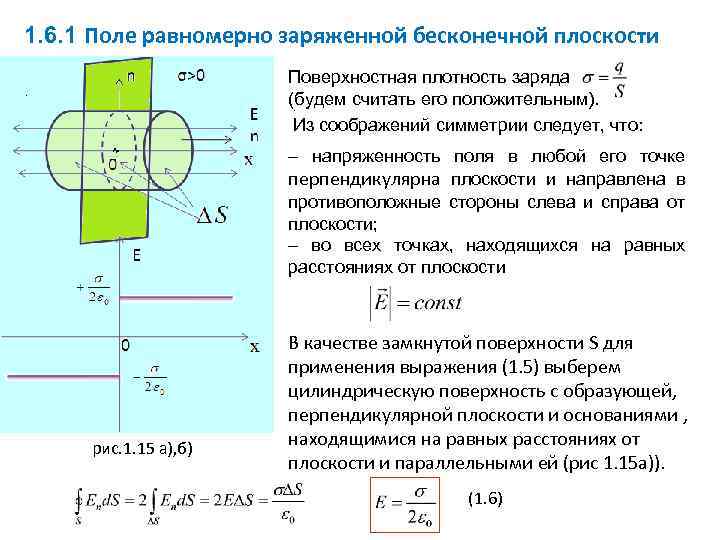1. 6. 1 Поле равномерно заряженной бесконечной плоскости Поверхностная плотность заряда (будем считать его положительным). . Из соображений симметрии следует, что: . – напряженность поля в любой его точке перпендикулярна плоскости и направлена в противоположные стороны слева и справа от плоскости; – во всех точках, находящихся на равных расстояниях от плоскости рис. 1. 15 а), б) В качестве замкнутой поверхности S для применения выражения (1. 5) выберем цилиндрическую поверхность с образующей, перпендикулярной плоскости и основаниями , находящимися на равных расстояниях от плоскости и параллельными ей (рис 1. 15 а)). (1. 6)

В проекции на ось OX напряженность поля можно записать так: Поле бесконечной равномерно заряженной плоскости однородно, но его напряженность при переходе через эту плоскость терпит разрыв (рис 1. 15 б)). 1. 6. 2 Поле двух бесконечных параллельных равномерно заряженных плоскостей Поле между плоскостями однородно, а слева и справа от плоскостей отсутствует (рис 1. 16 а), б)) (1. 7) рис 1. 16

1. 6. 3 Поле равномерно заряженной по поверхности сферы : ; Пусть сфера радиуса R равномерно заряжена с поверхностной плотностью : , где q – заряд на поверхности сферы. ; Из-за сферической симметрии распределения заряда напряженность поля в любой точке может иметь только радиальное направление. Поэтому в качестве замкнутой поверхности в выражении (1. 5) выбирается сфера, концентрическая данной. (1. 8) рис 1. 17 Напряженность поля внутри сферы равна нулю, скачком меняется на ее поверхности; вне сферы ее полностью совпадает с полем точечного заряда, если его расположить в центре сферы, а сферу убрать, при условии (рис 1. 17 б)).

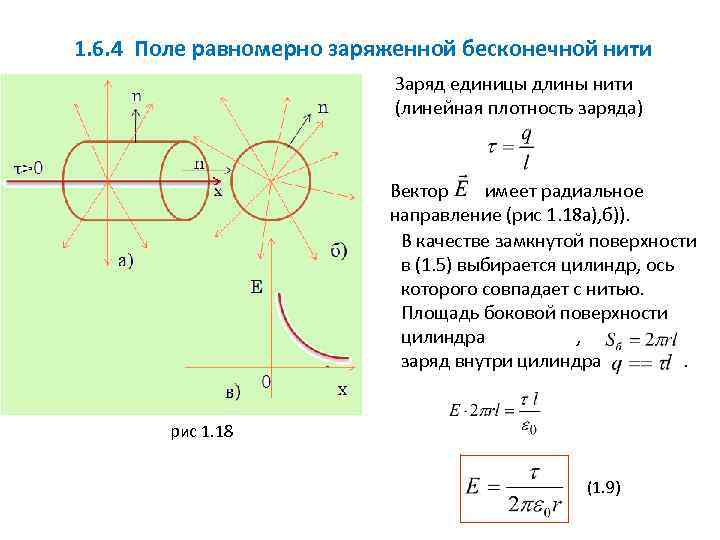1. 6. 4 Поле равномерно заряженной бесконечной нити Заряд единицы длины нити (линейная плотность заряда) Вектор имеет радиальное направление (рис 1. 18 а), б)). В качестве замкнутой поверхности в (1. 5) выбирается цилиндр, ось которого совпадает с нитью. Площадь боковой поверхности цилиндра , заряд внутри цилиндра. рис 1. 18 (1. 9)

1. 7 Дифференциальная форма теоремы Гаусса. Интегральной формой записи теоремы Гаусса (1. 5) удобно пользоваться для расчета полей высокой симметрии. В случае произвольного электростатического поля, не обладающего симметрией, используют дифференциальную форму теоремы Гаусса. Пусть заряд распределен в пространстве непрерывно и объемная плотность заряда является функцией координат: . Выберем достаточно малый объем , в пределах которого. Заряд, заключенный внутри этого объема Поток вектора через замкнутую поверхность S, охватывающую : Поделим обе части этого выражения на к нулю: и устремим .

(1. 10) Формула (1. 10) представляет собой дифференциальную форму записи теоремы Гаусса для напряженности электростатического поля. Выражение имеет смысл «удельной мощности» источников поля в в окрестности точки наблюдения. Т. о. из (1. 10) следует, что «удельная мощность» источников пропорциональна объемной плотности зарядов в окрестности данной точки поля. Можно сказать иначе: Число силовых линий, которые обрываются в некотором малом объеме в окрестности данной точки, пропорционально объемной плотности зарядов в этом объеме.