Электронный учебно-методический комплекс Твердотельная электроника МОСКВА

Электронный учебно-методический комплекс Твердотельная электроника МОСКВА 201 6 НИУ «МЭИ» Презентации к лекционному курсу Уравнение Шрёдингера, волновая функция Электронный учебно-методический комплекс

В 1924 г. французский физик Луи де Бройль предположил, что любая частица, в том числе и электрон, обладает волновыми свойствами с длиной волны ph где h =6, 62· 10 -34 Дж·с=4, 5· 10 -15 э. В·с – постоянная Планка; p – импульс электрона Луи Виктор Пьер Раймон, 7 -й герцог Брольи , более известный как Луи де Бройль ( фр. Louis-Victor-Pierre-Raymond, 7ème duc de Broglie, Louis de Broglie ; 15 08 1892 — 19 03 1987 ) — французский физик — теоретик , лауреат Нобелевской премии по физике за

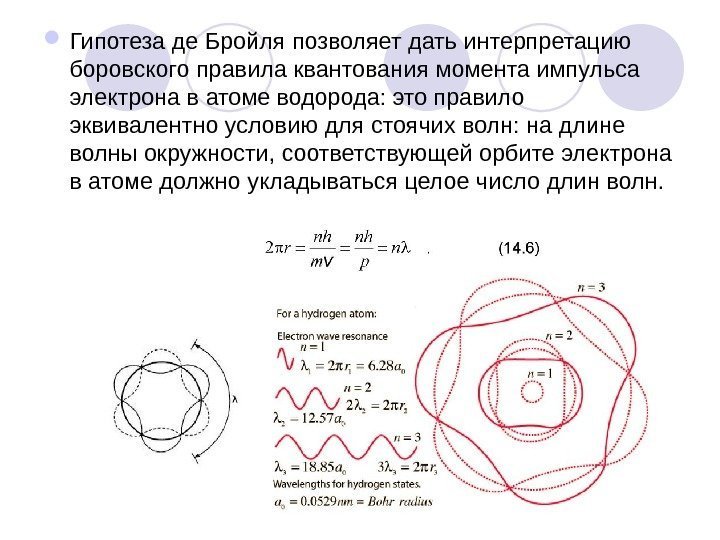
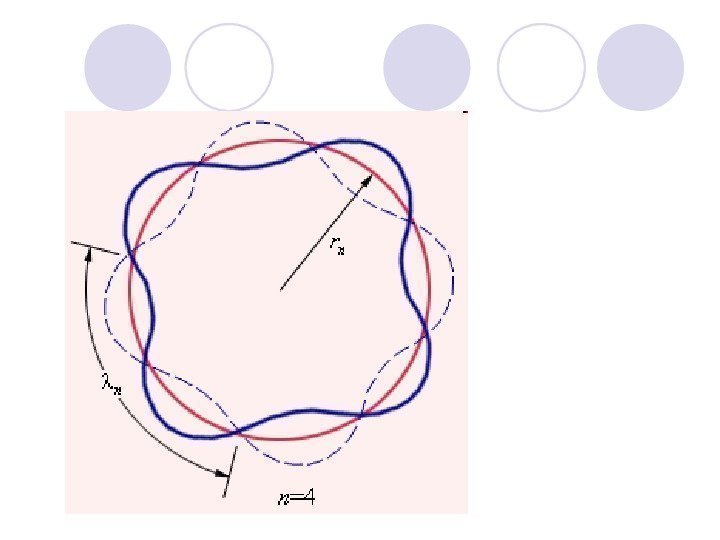
Гипотеза де Бройля позволяет дать интерпретацию боровского правила квантования момента импульса электрона в атоме водорода: это правило эквивалентно условию для стоячих волн: на длине волны окружности, соответствующей орбите электрона в атоме должно укладываться целое число длин волн.

pk 2 2 h. Можно ввести понятие волнового числа , то есть числа волн, укладывающихся на 2 см = 1, 054· 10 -34 Дж с – приведенная постоянная Планка или постоянная Дирака kp Тогда можно связать импульс с волновым вектором: p. В этом случае называют квазиимпульсом электрона

Кинетическая энергия свободного электрона 0 22 0 22 2 mkmpcp ck chc hcm. E 0 m =9, 1 10 -31 кг – масса свободного электрона

В 1926 г. австрийский физик Эрвин Шрёдингер вывел уравнение для волн де Бройля. Волна, связанная с отдельной частицей описывается волновой функцией, зависящей от координат и времени ), (tr ), (H , tr t tr i (2) В левой части – скорость изменения волновой функции, умноженная на мнимую единицу ( ) и приведенную постоянную Планка. В правой – оператор Гамильтона Ĥ , действующий на волновую функцию 12 i

Уравнение Шрерингера рвин Р дольф Й зеф ЭЭу. Э о. Э Алекс ндр Шрёдингер а. Э ( нем. Erwin Rudolf Josef Alexander Schrödinger 12 08 1887 — 4 01 1961 ) — австрийский физик-теоретик, Лауреат Нобелевской премии по физик е ( 1933 )

Квантовые операторы − символические изображения математических операций преобразования величин в квантовой теории. В квантовой механике постулируется, что каждой физической величине, описываемой в классической механике функцией F ( x, y, z, px, py, pz ) координат и импульсов, ставится в соответствие линейный оператор действующий на волновую функцию . Под оператором понимается правило, по которому одной функции переменных сопоставляется другая функция тех же переменных ), , , ( ˆ ), , , (tzyx. Ftzyx zyx. Fˆ, ˆ, ˆˆ ), , , (tzyx Fˆ ), , , (tzyx, , , ), , , (tzyx

Например: оператор может означать дифференцирование по какой-либо переменной x tzyx. Ftzyx ), , , (ˆ), , , ( x F ˆ

Примеры некоторых операторов Оператор координаты равен самой координате x , т. е. сводится к умножению на эту переменную: Оператор полной энергии (гамильтониан) Ĥ получается из выражения где E – собственная энергия частицы (системы частиц). xˆ xxˆ ), (ˆtr. EH ), ( , tr. E t tr i

Энергия частицы массой имеет две составляющие – кинетическую и потенциальную: В этом случае , где − оператор кинетической энергии, − оператор потенциальной энергии. 0 m пk UEE UEHˆˆˆE ˆ U ˆ 0 222 00 2 2 1 ˆˆˆ 2 1 2 ˆ ˆ m ppp mm p Ezyx

Свободная частица массы m 0 : 2 0 2 2 ˆ m H 2 2 2 2 iiizyx — оператор Лапласа Примеры некоторых гамильтонианов

Примеры некоторых гамильтонианов Частица в одномерной потенциальной яме U(x), 0 < x < w : x. U dx d m H 2 2 0 2 2 ˆ

Кинетическая энергия Если заменить в правой части уравнения величину импульса на так называемый оператор импульса , – оператор Гамильтона или набла 0 2 2 mp. Ek i i pˆ k z j y i xiii

операторы проекций импульсов x ip x ˆ y ip y ˆ z ip z ˆ

уравнения для собственных функций и собственных значений операторов проекций импульсов zzz yyy xxx pzpp pypp pxpp p z i zi p y i yi p x i xi ˆ )3(ˆ ˆ

Решением первого уравнения системы является волновая функция xip p x x ezy, 0 где zy, 0 — произвольная функция ( y, z ) ), ( 22 2 0 2 tr. E r tr m — уравнение Шредингера для свободной частицы

Уравнение Шредингера для свободной частицы Решения уравнения Шрёдингера существуют только для волновых функций, характеризуемых набором целых чисел (которые называют квантовыми): n, l, m и соответствующих им дискретных значений энергий ), ( 2 2 2 0 2 tr. E r tr m

Уравнение Шредингера для свободной частицы В стационарном случае Шредингер заметил, что при определенных условиях решение его волнового уравнения представляют собой стоячие волны , и связал эти решения со стационарными состояниями атомов. 0), ( 2 , 2 0 2 tr. Etr mt tr i

Учитывая потенциальную энергию электрона Это уравнение в частных производных имеет множество решений. В каждой конкретной задаче из этого множества следует выбрать одно решение, отвечающее условиям задачи ), ()(), ( 2 2 0 2 tr. Etrr. Utr m

В любой момент времени t , состояние квантовой частицы задается двумя величинами: координатами (радиусом-вектором) и импульсом: t. Erpi trtr exp), (0 h. E – энергия свободного электрона, T 2 2 – циклическая частота, T – период. (4)

Волновая функция t. Erp i trtr exp), (0 )]sin()[cos(), ( )](exp[), ( 0 0 trkitrktr trkitrtr Это – комплексная синусоида.

Решения в виде стоячей волны зависят от времени благодаря множителю , причем возможные значения частоты образуют дискретный ряд , . . . , и, таким образом, энергия п -го стационарного состояния равна]exp[ti 12 nn.

Волновая функция)5)]((exp[), (0 trkitrtr Если нам известна волновая функция (5), то из нее можно получить энергию, продифференцировав ее по времени один раз и квадрат импульса продифференцировав ее по координате дважды: ), ( 2 2 tr. E i t tr tr p r tr

Волновая функция 2 22 2), (r tr tr p t tr tri E ), ( 1), ( 2), ( 1 ), ( 2), ( 1 ), ( 2 2 0 2 tr r tr mt tr tri r tr mtr tritr. E 0 2 2 m p

Как определить саму волновую функцию? в соответствии с соотношением неопределенностей немецкого физика Вернера Гейзенберга, выведенного им в 1927 г. , координату и импульс любой микрочастицы нельзя измерить точно одновременно: (для одномерного движения, чем точнее значение координаты, тем менее точно можно измерить значение импульса) hpx

В рнер Карл Г йзенберге. Э ( нем. Werner Karl Heisenberg ; 5 12 1901 — 1 02 1976 ) — немецкий физик — теоретик , лауреат Нобелевской премии по физике ( 1932 )

Максимум, что можно сделать – это определить три координаты или три компоненты импульса, а затем из уравнения Шрёдингера вычислить волновую функцию в какой угодно последующий момент времени. При решении конкретных задач уравнение Шредингера должно быть дополнено заданием начальных условий: для момента времени t =0, т. е. нужно задать функцию)0, (), (0 rtr

Так что такое волновая функция? В 1926 г. немецкий физик Макс Борн предложил, что волновая функция физического смысла не имеет, но определяет вероятность пребывания электрона в заданной точке. В тех областях, где амплитуда волны больше, обнаружение электрона более вероятно.

Макс Борн ( нем. Max Born ; 11 12 1882 — 5 01 1970 ) — немецкий и британский физик -теоретик и математик , Лауреат Нобелевской премии п о физике ( 1954 )

Волновая функция Шредингеровская волновая функция (амплитуда волны де Бройля) определяет вероятность нахождения частицы в данной точке пространства и времени. Если мы пытаемся установить положение частицы в данный момент времени t , то вероятность обнаружить частицу в малом объеме пропорциональна rdd. V 3 rtr. Vtr 3 22 d), (

Вероятность обнаружить данную частицу в объеме d. V здесь – комплексно-сопряженная с функцией . Согласно Постулата № 1 квантовой механики Состояние частицы (или системы частиц) задано, если известна волновая функция *), (), ( 2 trtrtrw *), (tr )](exp[)*, (0 trkitr

Для свободной частицы =0 r. U kxti. Bkxti. Axexpexp)( Emрk 022 E Таким образом, для свободной частицы общее решение представляется в виде двух монохроматических волн, распространяющихся вдоль оси Х в противоположных направлениях с амплитудами А и В соответственно

Если взять волну де Бройля, идущую в сторону положительных значений оси Х, то и значит, плотность вероятности нахождения частицы не зависит от координаты. 2 )*, (), (Аtrtr

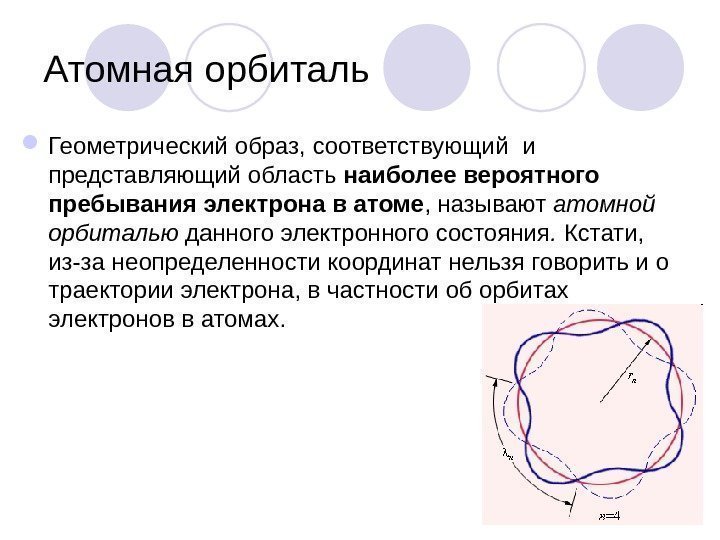
Атомная орбиталь Геометрический образ, соответствующий и представляющий область наиболее вероятного пребывания электрона в атоме , называют атомной орбиталью данного электронного состояния. Кстати, из-за неопределенности координат нельзя говорить и о траектории электрона, в частности об орбитах электронов в атомах.

При условии стационарности поля внешних сил ( ) волновую функцию можно представить в следующем виде: , что дает возможность после разделения переменных получить два уравнения для временной и координатной частей функции соответственно. Так для одномерного случая уравнение можно записать в виде: constt. Е ), (tr trtr)(), ( t tx itxx. Е x tx m , ), (

После разделения переменных можно получить два уравнения для временной и координатной частей функции соответственно: t t it. Е )( )()( 2 2 2 0 2 xx. UEx dx d m 0)()( 2 2 2 0 2 xx. UEx dx d m 0)( 2 0 2 2 xx. UE m dx xd

Решение уравнения с точностью до множителя С будет иметь во всех случаях один и тот же вид: Для нахождения вида функции в уравнение необходимо подставлять зависимость в каждом конкретном случае. Однако точное решение уравнения можно получить только для некоторых причем, обычно это удается сделать лишь при определенных (собственных) значениях энергии Е. t E i. Сt exp )(x x. U

Решение уравнение Шредингера частицы, находящейся в потенциальной яме ax ax x x. U , 0, 0), ( 2)( 2 0 2 2 tx. E m dx xd ax 0 0)0(0)(а

Решение уравнение Шредингера частицы, находящейся в потенциальной яме Вводя обозначение В =0 E m k 2 02 0)( )(2 2 2 xk dx xd аxkx. Bkx. Aх0, cossin)(2 00 sin)(Aa 0 sinkа. Ankа 0)0( аnk

Решение уравнение Шредингера частицы, находящейся в потенциальной яме Заметим, что условие соответствует образованию в области стоячей волны , когда в пределах этой области укладывается полуволн аnk ax 0 k 2 2 a n

Решение уравнение Шредингера частицы, находящейся в потенциальной яме где n =1, 2, 3… 2 2 22 *2 n аm E n

Решение уравнение Шредингера частицы, находящейся в потенциальной яме Случай п= 0 следует отбросить, так как при этом волновая функция всюду равна пулю, что лишено физического смысла, так как это означает, что частица в яме отсутствует. Состояние частицы, в которой она обладает наименьшей энергией ( п= 1), называется основным состоянием. Все остальные состояния являются возбужденными.

Решение уравнение Шредингера частицы, находящейся в потенциальной яме 2 22 1 2 аm E n 12 *2 *21 *2 222 2 222 1 n аmnnn аm. EEE nn nnnnn

Решение уравнение Шредингера частицы, находящейся в потенциальной яме Как энергия состояния, так и разность энергий соседних состояний ( – расстояние между уровнями энергии) увеличивается с ростом уровня п и зависит от массы частицы и ширины потенциальной ямы: с увеличением массы (переход к макрообъектам) и ширины области, в которой заключена частица (переход к свободным частицам), расстояние между уровнями энергии уменьшается и в пределе становится равным нулю, другими словами, значения энергий для свободных микрочастиц и макрообъектов не квантуются. n.

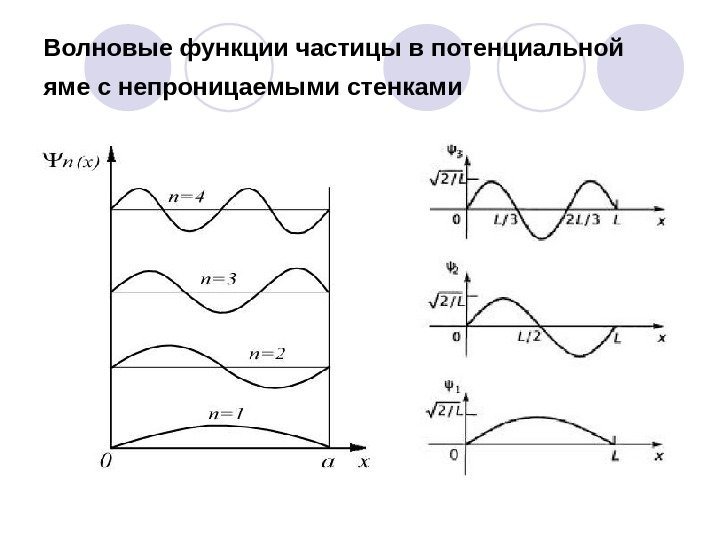
Решение уравнение Шредингера частицы, находящейся в потенциальной яме Каждому значению соответствует собственная волновая функция a nx Ax sin)( 1 2 sin, 2 0 222 a Аn a x Аtx а п а. А 2 n a xп sin

Волновые функции частицы в потенциальной яме с непроницаемыми стенками

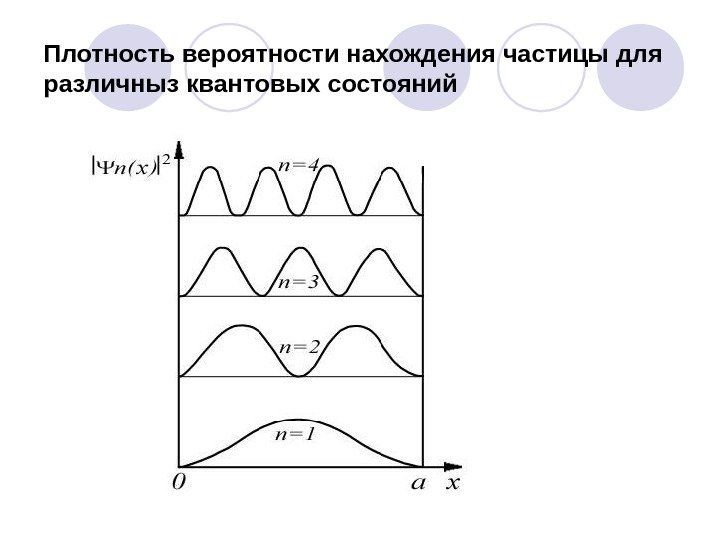
Плотность вероятности нахождения частицы для различныз квантовых состояний

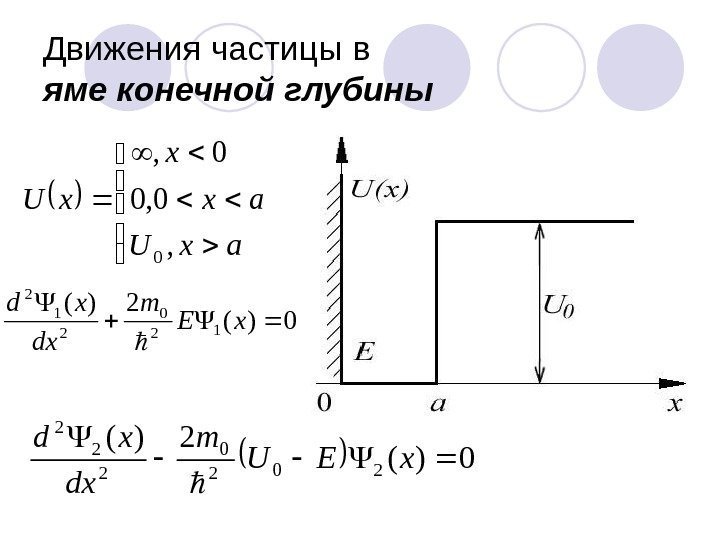
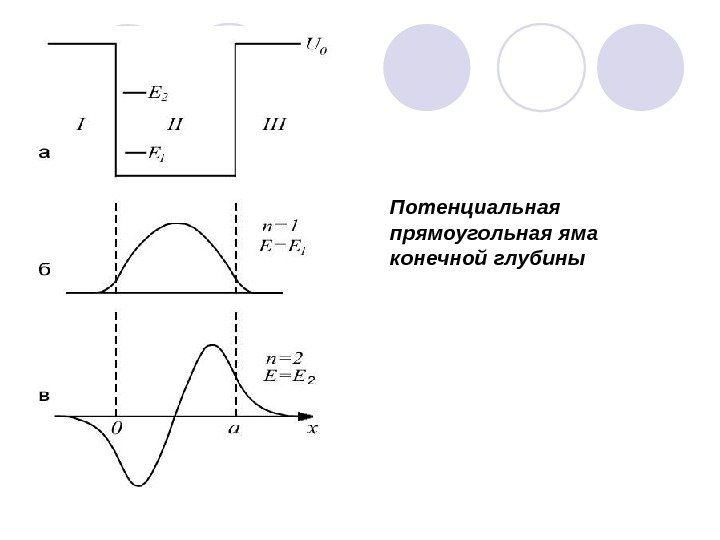
Движения частицы в яме конечной глубины ax. U ax x x. U , 0, 0 0)( 2)( 12 0 2 1 2 x. Е m dx xd 0)( 202 0 2 2 2 x. ЕU m dx xd

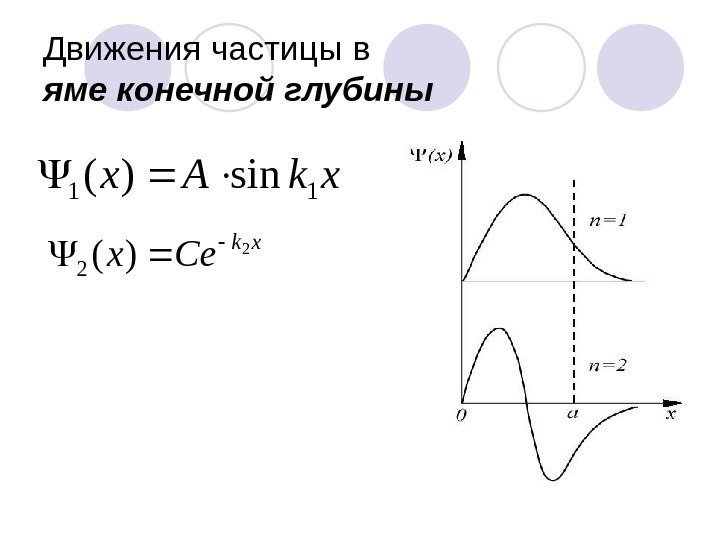
Движения частицы в яме конечной глубиныхk Сех 2 )(2 xk. Ax 11 sin)(

Потенциальная прямоугольная яма конечной глубины ax. U ax x. U , 0, 0 0 0)( 2)( 3, 102 0 2 3, 1 2 x. ЕU m dx xd EU m k 02 0 1 2 0)()( 3, 12 1 2 3, 12 xk dx xd 0)( 22 0 2 2 2 x. Е m dx xd . , exp)( ; 0, sin)( ; 0, exp)( 133 22 111 аxxk. Bх axxk. Сx xxk. Ax

Потенциальная прямоугольная яма конечной глубины

Туннельный эффект Как было показано, решение уравнения Шредингера для свободной частицы ( U =0) дает одинаковую плотность вероятности обнаружения частицы в любой точке пространства. Каково поведение частицы, встречающей на своем пути потенциальный барьер?

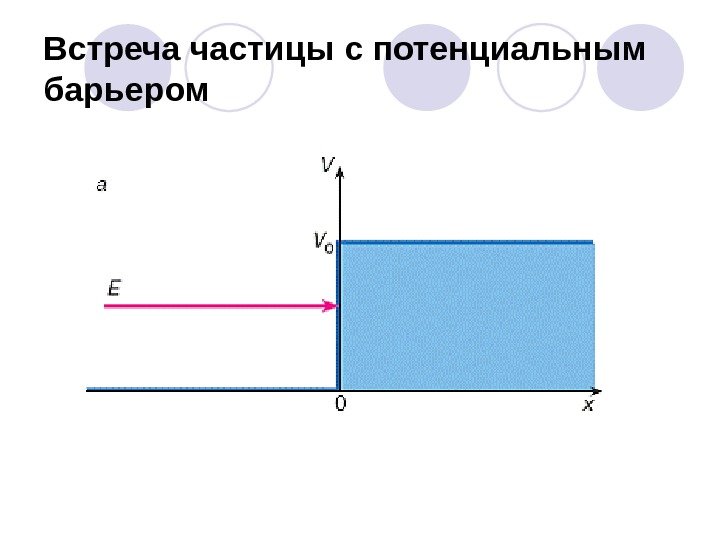
Встреча частицы с потенциальным барьером

Встреча частицы с потенциальным барьером В рамках классической механики априорно ясно, что тело имеющее полную энергию Е не может преодолеть потенциал V 0 , при условии V 0>Е. При падении тела на такой барьер оно может лишь полностью отразиться от него независимо от его формы и ширины. Это согласуется с законом сохранения энергии. Если энергия частицы больше высоты потенциального барьера, то частица обязательно проходит над ним.

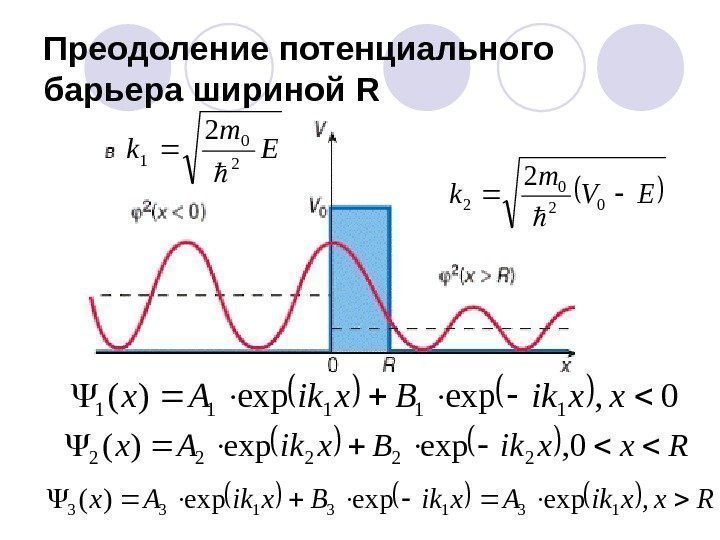
Встреча частицы с потенциальным барьером Туннельный эффект является принципиально квантово-механическим эффектом, не имеющим аналогов в классической физике. Рассмотрим случай одномерного прямоугольного барьера шириной R

Преодоление потенциального барьера шириной R 0, expexp)(11111 xxik. Bxik. Ax Rxxik. Axik. Bxik. Ax, expexpexp)(1313133 Rxxik. Bxik. Ax 0, expexp)(22222 Е m k 2 0 1 2 EV m k

Преодоление потенциального барьера шириной R Отношение квадратов модулей амплитуд отраженной и падающей волн определяет коэффициент отражения частицы от потенциального барьера: 2 21 21 2 1 пад от I I kk kk AB r

Коэффициент прохождения D (коэффициент прозрачности), определяющий часть потока частиц, прошедшего сквозь барьер, связан с коэффициентом отражения: r.

Встреча частицы с потенциальным барьером Рассмотрение случая высокого потенциального барьера ( ) проводится аналогично, но теперь является мнимой величиной: 0 VE 2 k ik. VE m k

Полагая В 2 =0 (отражением от второй границы барьера можно пренебречь при условии достаточно высокого и широкого потенциального барьера), получаем выражения для пси-функции и коэффициента прозрачности: kx. Axexp)(

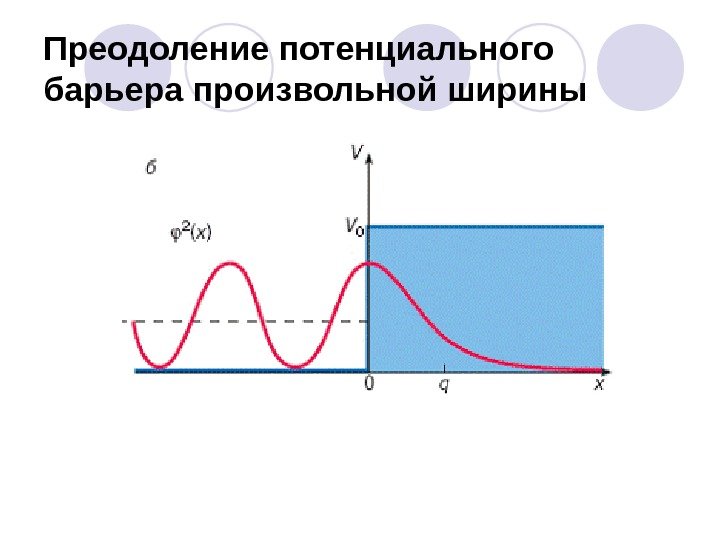
Преодоление потенциального барьера произвольной ширины

Можно показать, что для высокого потенциального барьера любой формы коэффициент прозрачности , то есть имеется вероятность проникновения частицы сквозь такой барьер. Частица как бы просачивается ( «туннелирует» ) через область потенциального барьера, не изменяя при этом свою энергию. Это явление называется туннельным эффектом.

Вероятность туннелирования уменьшается с ростом ширины барьера, его высоты (точнее, разности ) и с увеличением массы частицы. Например, если электрон ( m 0 =9, 1∙ 10 -31 кг) с энергией Е =1 э. В может преодолеть прямоугольный потенциальный барьер высотой =2 э. В и шириной R =10 -8 см (размер атома) и при этом коэффициент прозрачности барьера 0, 78, то уже для протона ( m п=1, 67∙ 10 -27 кг) при тех же условиях коэффициент прозрачности барьера 3, 6∙ 10 -19. EV

Основы теории туннельных переходов заложены работами советских ученых Л. И. Мандельштама и М. А. Леонтовича в 1928 г.

Квантовый осциллятор Известно, что гармонический осциллятор, то есть система, совершающая гармонические колебания с круговой частотой , вызываемые квазиупругой силой имеет потенциальную энергию где k – коэффициент пропорциональности (в случае упругих сил – коэффициент упругости), m – масса этой системы. , mk kx. F 22 222 xmkx U

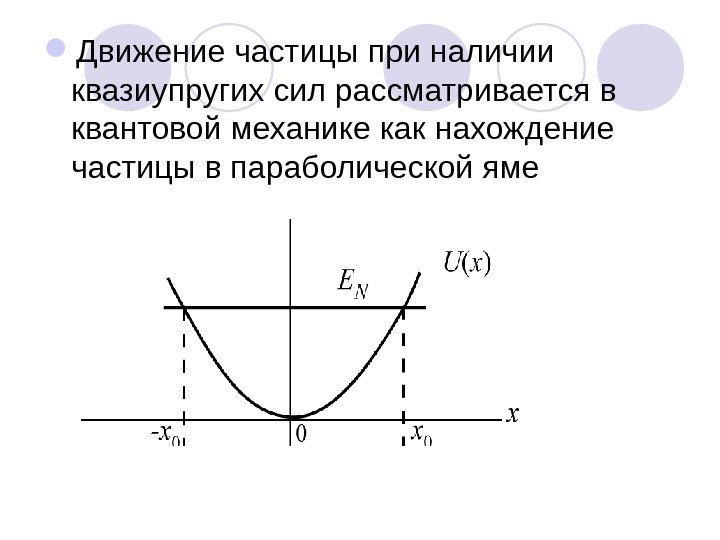
Движение частицы при наличии квазиупругих сил рассматривается в квантовой механике как нахождение частицы в параболической яме

Гамильтониан для потенциальной энергии примет вид: 2 22 xm U 22 ˆ 22 2 22 xm dx d m H 0)( 2 2)( 22 22 2 x xm Е m dx xd

Вводя величины где n =0, 1, 2, 3… 02 Е 00 0 m х 0 х x 0)( )(2 2 2 x d xd 12 n

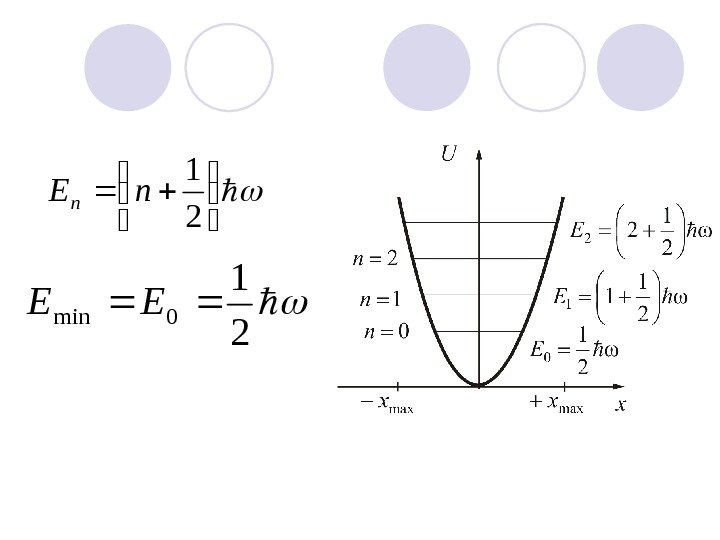
2 1 n. En 2 1 0 min.

Отметим, что уровни гармонического квантового осциллятора, в отличие от случая прямоугольной потенциальной ямы, расположены на равных расстояниях друг от друга, причем, на основании подсчета вероятности разных переходов оказывается, что возможны переходы системы только в соседние энергетические состояния (выполняется правило отбора: ) с испусканием или поглощением кванта энергии 1 n

Приведем вид волновых функций для первых трех энергетических уровней гармонического осциллятора: 2 02 00 2 exp 1 )( хх хx 2 00 1 2 exp 2 2 1 )( х х х x 2 0 2 0 2 2 exp 2 4 8 1 )( х х х x n =0, , n = 1 , n = 2 ,

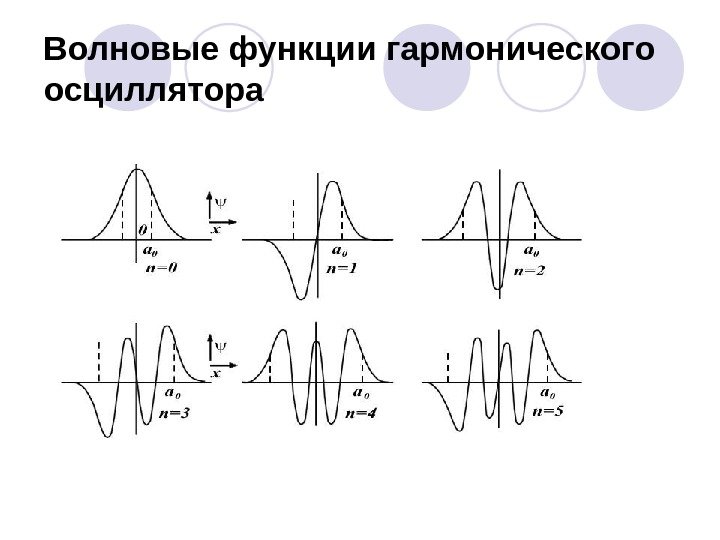
Волновые функции гармонического осциллятора

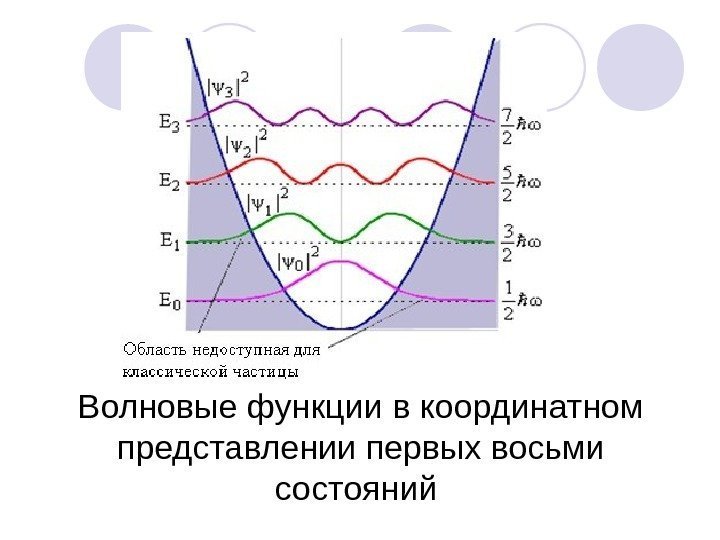
Отметим, что вне классической области волновые функции отличны от нуля, что свидетельствует о том, что квантовый гармонический осциллятор с определенной вероятностью может находиться вне пределов параболической потенциальной ямы. 00, аа

Волновые функции в координатном представлении первых восьми состояний

Сколько электронов может находиться на одной орбите? Вольфганг Паули в 1925 г. сформулировал принцип запрета : на любой атомной орбите может находиться не более двух электронов. Если бы этого не наблюдалось, все электроны в сложных атомах перешли бы на самый нижний энергетический уровень. Вольфганг Паули

В 1940 г. тот же Паули выдвинул теорему, согласно которой для частиц с полуцелым спином ( фермионов ) выполняется принцип запрета (на одной орбитали находится не более 2 s +1 частиц). У фотона, глюона (осуществляет обмен между кварками) s =1 – целое число, в одном состоянии может находиться любое число частиц.

Свое название – фермионы , частицы с полуцелым спином (электроны, дырки) получили по имени итальянского физика Энрико Ферми. Энр ко Ф рмии. Э е. Э ( итал. Enrico Fermi ; 29. 09. 1901 , Рим , Италия — 28. 11. 1954 , Чикаго , США) — итальянский физик. Лауреат Нобелевской премии по физике 1938 года

Частицы с целым спином (включая нуль) – бозоны , по имени индийского ученого Шатьендраната Бозе. Сатьендра Нат Б зео. Э (англ. Satyendra Nath Bose ) или Шотендронат Б шу о. Э (бенг. সসসসস সসস , o en rona ʃ t tː dt t tʰ bo u) ( ʃ 0 1. 01. 1894, Калькутта — 0 4. 02 1974) — индийский физик