Электронный Парамагнитный Резонанс Электронный

Электронный Парамагнитный Резонанс

Электронный парамагнитный резонанс В основе метода лежит резонансное поглощение электромагнитного излучения неспаренными электронами, помещенными в магнитное поле. Ps Атом водорода ms P l ml Электрон в атоме участвует в двух видах движения: 1. Орбитальном (l) - вокруг ядра атома. 2. Спиновом (s) - вокруг собственной оси. Каждый вид движения можно охарактеризовать двумя моментами: 1. Магнитным (m), отражающим движение заряженной частицы. 2. Механическим (P), отражающим движение материальной частицы.

Взаимосвязь механического и магнитного моментов Из классической механики известно, что момент количества движения электрона Ps на круговой орбите радиуса R ms P=mv. R, где m - масса электрона, а v - его скорость. P l ml Движение заряженной частицы по такому же контуру, создает магнитный момент, подобный тому, что возникает при движении тока m=IS, где I - сила тока в контуре (I=ve/2 p. R), а S - площадь контура (S=p. R 2) или m=ve. R/2 или, учитывая (P=mv. R) m=-e. P/2 m (или m/P=-e/2 m) Из квантовой механики известно, что P=nh/2 p, где n - главное квантовое число. Тогда при n=1 получим m=-eh/4 pm=b (магнетон Бора)

Суммарный магнитный момент Таким образом, для орбитального движения ml/Pl=-e/2 m Для спинового движения ms/Ps=-e/m Суммарный магнитный момент равен: mj=ml+ms, А суммарный механический равен: Pj=Pl+Ps Однако mj/Pj ml/Pl ms/Ps поэтому вводят коэффициент пропорциональности (g) mj/Pj=-g*e/2 m, где g это g-фактор, т. е. коэффициент, показывающий вклад орбитального и спинового момента в суммарный момент. В конечном итоге, поскольку ml ms, то mj ms и mj -g*e/2 m*h/2 p*S =-gb. S

Энергия электрона в магнитном поле равна E=m*H*cos(m, H), где m - суммарный магнитный момент электрона, H - напряженность магнитного поля, cos(m, H) - угол между векторами m и H (обычно = 1 или -1), тогда подставив значение m получим E=-gb. SH, Где S - спиновое квантовое число = +1/2 или -1/2. В итоге E=± 1/2 gb. H

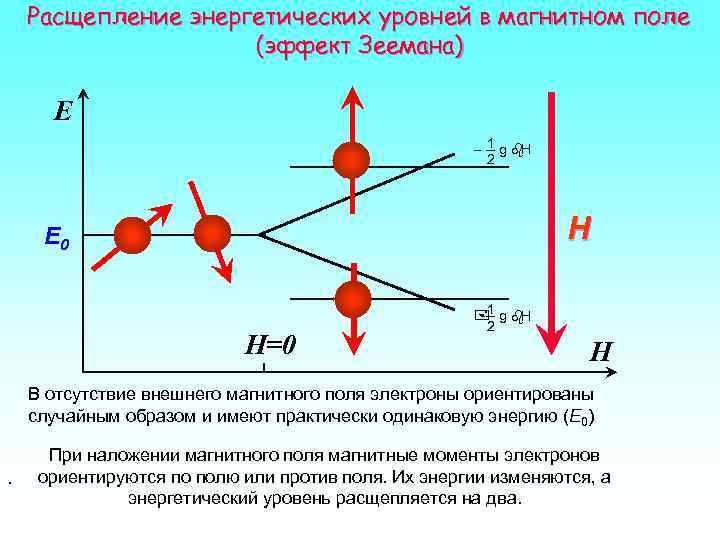
Расщепление энергетических уровней в магнитном поле (эффект Зеемана) E - 1 g H 2 E 0 H 1 g H 2 H=0 H В отсутствие внешнего магнитного поля электроны ориентированы случайным образом и имеют практически одинаковую энергию (E 0) При наложении магнитного поля магнитные моменты электронов. ориентируются по полю или против поля. Их энергии изменяются, а энергетический уровень расщепляется на два.

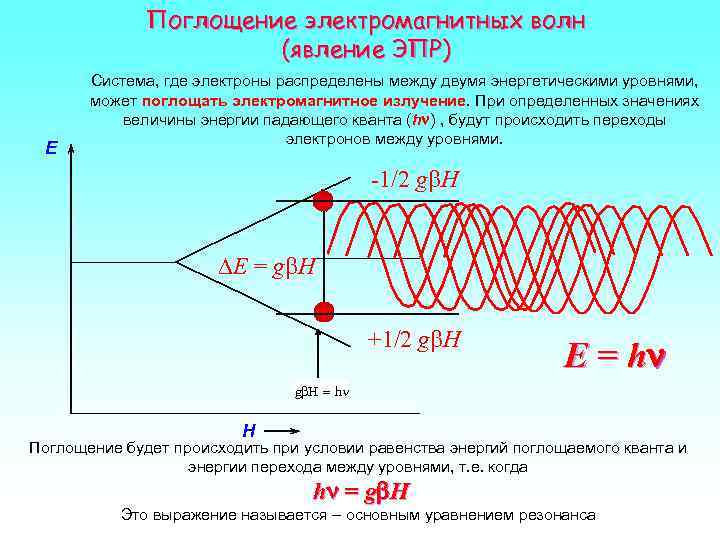
Поглощение электромагнитных волн (явление ЭПР) Система, где электроны распределены между двумя энергетическими уровнями, может поглощать электромагнитное излучение. При определенных значениях величины энергии падающего кванта (hn) , будут происходить переходы электронов между уровнями. E -1/2 gb. H DE = gb. H +1/2 gb. H E = hn gb. H = hn H Поглощение будет происходить при условии равенства энергий поглощаемого кванта и энергии перехода между уровнями, т. е. когда hn = gb. H Это выражение называется – основным уравнением резонанса

Разность между числом электронов (заселенностью) на двух разных энергетических уровнях в парамагнетиках определяется уравнением Больцмана:

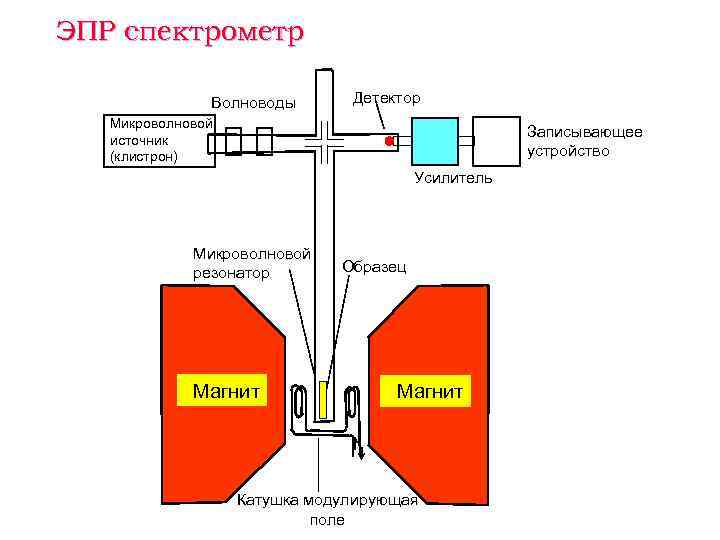
ЭПР спектрометр Волноводы Детектор Микроволновой источник Записывающее (клистрон) устройство Усилитель Микроволновой резонатор Образец Магнит Катушка модулирующая поле

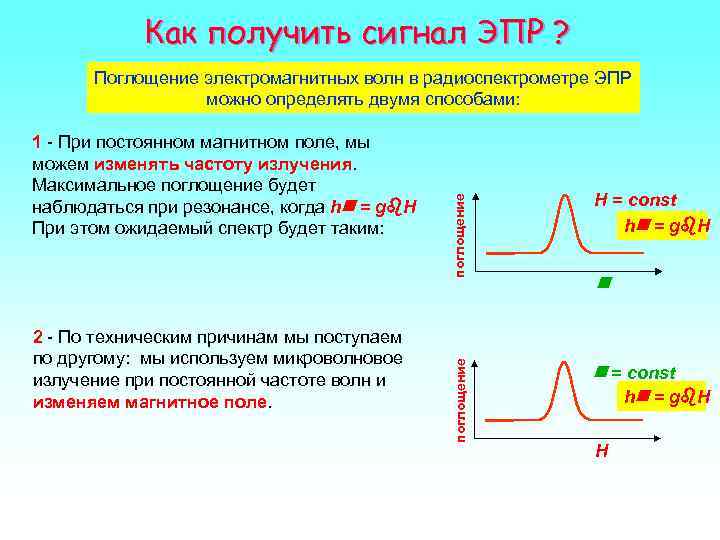
Как получить сигнал ЭПР ? Поглощение электромагнитных волн в радиоспектрометре ЭПР можно определять двумя способами: 1 - При постоянном магнитном поле, мы можем изменять частоту излучения. Максимальное поглощение будет H = const поглощение наблюдаться при резонансе, когда h = g H При этом ожидаемый спектр будет таким: h = g H 2 - По техническим причинам мы поступаем по другому: мы используем микроволновое поглощение излучение при постоянной частоте волн и = const изменяем магнитное поле. h = g H H

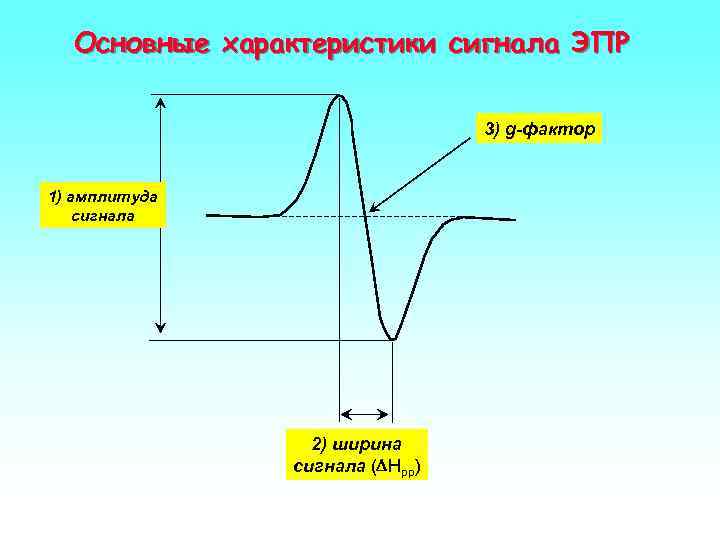
Основные характеристики сигнала ЭПР 3) g-фактор 1) амплитуда сигнала 2) ширина сигнала (DHpp)

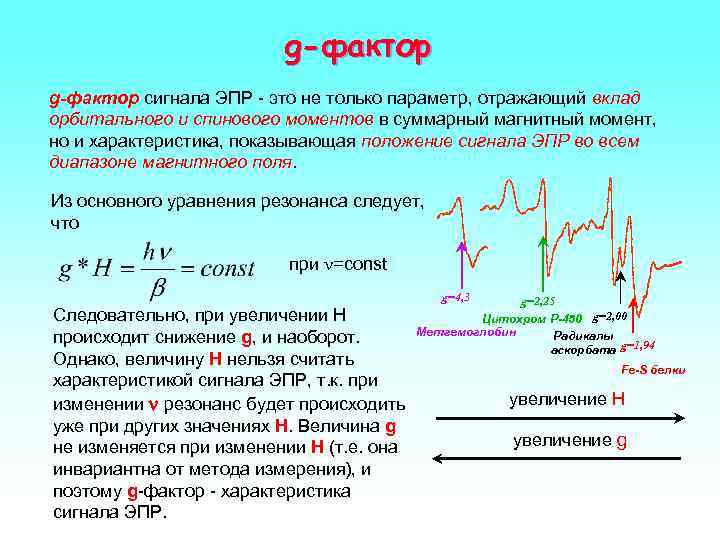
g-фактор сигнала ЭПР - это не только параметр, отражающий вклад орбитального и спинового моментов в суммарный магнитный момент, но и характеристика, показывающая положение сигнала ЭПР во всем диапазоне магнитного поля. Из основного уравнения резонанса следует, что при n=const g=4, 3 g=2, 25 Следовательно, при увеличении H Цитохром P-450 g=2, 00 Метгемоглобин происходит снижение g, и наоборот. Радикалы аскорбата g=1, 94 Однако, величину Н нельзя считать Fe-S белки характеристикой сигнала ЭПР, т. к. при изменении n резонанс будет происходить увеличение H уже при других значениях Н. Величина g не изменяется при изменении Н (т. е. она увеличение g инвариантна от метода измерения), и поэтому g-фактор - характеристика сигнала ЭПР.

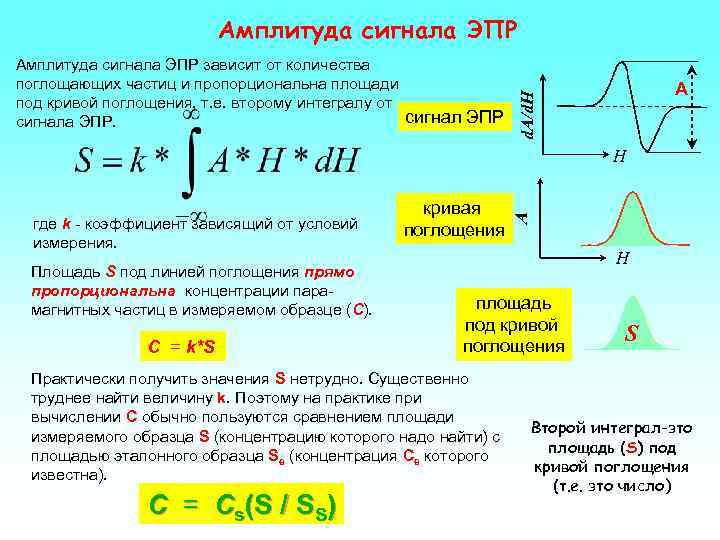
Амплитуда сигнала ЭПР зависит от количества поглощающих частиц и пропорциональна площади А d. A/d. H под кривой поглощения, т. е. второму интегралу от сигнала ЭПР. сигнал ЭПР H кривая A где k - коэффициент зависящий от условий поглощения измерения. H Площадь S под линией поглощения прямо пропорциональна концентрации пара- магнитных частиц в измеряемом образце (C). площадь под кривой поглощения S C = k*S Практически получить значения S нетрудно. Существенно труднее найти величину k. Поэтому на практике при вычислении С обычно пользуются сравнением площади Второй интеграл-это измеряемого образца S (концентрацию которого надо найти) с площадь (S) под площадью эталонного образца Se (концентрация Ce которого кривой поглощения известна). (т. е. это число) C = Cs(S / SS)

Ширина сигнала ЭПР определяется взаимодействием магнитных моментов электрона с окружением. d. A/d. H Теоретически минимальная ширина линии следует из соотношения неопределенностей Гейзенберга: DH где D t - время измерения и DE - неопределенность энергии системы. Рассматриваемый процесс - это поглощение электромагнитного кванта, такое, что D t может быть интерпретировано как время нахождения электрона на верхнем энергетическом уровне (время релаксации T ), а D E как энергия системы нашем случае = gb. H, отсюда h 1 DH ³ * 2 pgb T g

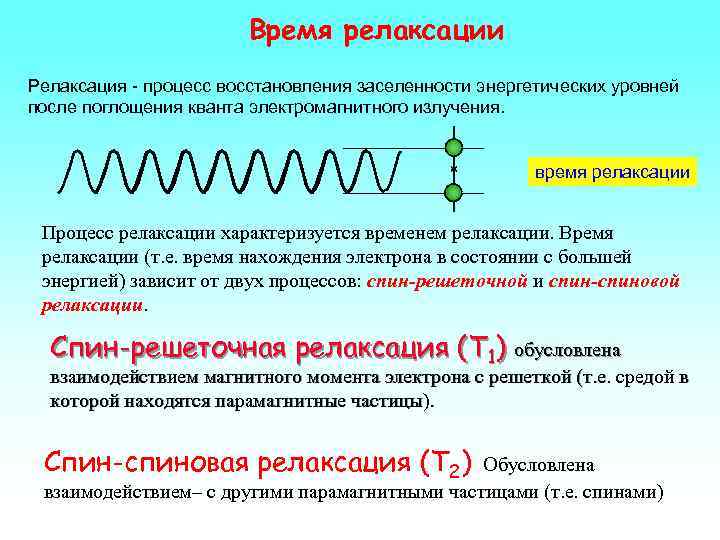
Время релаксации Релаксация - процесс восстановления заселенности энергетических уровней после поглощения кванта электромагнитного излучения. время релаксации Процесс релаксации характеризуется временем релаксации. Время релаксации (т. е. время нахождения электрона в состоянии с большей энергией) зависит от двух процессов: спин-решеточной и спин-спиновой релаксации. Спин-решеточная релаксация (T 1) обусловлена взаимодействием магнитного момента электрона с решеткой (т. е. средой в которой находятся парамагнитные частицы). Спин-спиновая релаксация (Т 2) Обусловлена взаимодействием– с другими парамагнитными частицами (т. е. спинами)

h 1 DH³ * 2 pgb T Большое T Малое T Малое DH Большое DH Зависимость суммарного времени релаксации (Т) от Т 1 и Т 2 выражается формулой: Тогда выражение для ширины сигнала ЭПР будет выглядеть так: