Электронное строение твердых тел Многие физические и химические

Электронное строение твердых тел Многие физические и химические свойства твердых тел можно понять только после изучения электронного строения и природы сил связи.

• Одна из главных задач любой теории твердого тела состоит в том, чтобы объяснить почему твердые тела могут принадлежать к столь различным по свойствам классам как проводники (металлы), полупроводники и диэлектрики, которые по электропроводимости могут отличаться в 1030 раз!

• Различие в электропроводимости между металлами, полупроводниками и диэлектриками : металлы обладают высокой электропроводностью ( = 104 – 106 (Ом см)-1), диэлектрики низкой проводимостью или почти полным ее отсутствием ( 10 -15 (Ом см)-1), полупроводники занимают промежуточное положение ( =10 -5 – 103 (Ом см)-1)

• Кроме различия в величинах электропроводимости принципиальное существует отличие в механизме электропроводности металлов, диэлектриков и полупроводников Так, и проводимость диэлектриков резко возрастает с ростом температуры, тогда как у металлов она слабо, но постоянно уменьшается.

• Электропроводность связана с концентрацией n, зарядом е и подвижностью носителей заряда: • = ne • Поэтому температурная зависимость будет определяться зависимостями n, e, и . температурными

• Для всех электронных проводников заряд е постоянен и не зависит от температуры. В большинстве материалов подвижность слабо уменьшается с ростом температуры из-за рассеяния кристаллической электронов решетки. электропроводности на Поэтому металлов и колебаниях различие в диэлектриков и полупроводников связано с различной концентрацией носителей заряда и ее температурной зависимостью

• В металлах концентрация носителей заряда п велика и неизменна при изменении температуры. • В полупроводниках и диэлектриках n экспоненциально растет с температурой и быстро растет с увеличением температуры. • В диэлектриках величина п очень мала. При высоких температурах проводимость диэлектриков может достигать проводимости полупроводников из-за роста п. • При низких температурах полупроводники могут стать диэлектриками

• Полупроводниковые материалы можно разделить на две группы. • I. Элементарные полупроводники, такие как кремний, германий, которые находятся в IV группе периодической системы. С ростом атомного номера элемента происходит переход от изолятора – алмаз к полупроводникам Si, Ge, Sn (серое) и далее к металлам – белое олово, свинец.

• За исключением двух последних все эти вещества имеют структуру алмаза, в которой каждый атом находится в тетраэдрическом окружении других атомов. Тетраэдры сочленяются друг с другом своими вершинами и образуют жесткий трехмерный каркас кубической симметрии. Видимо такая структура выгодна для проявления полупроводниковых свойств.

• II. Полупроводниковые соединения к ним относятся многие некоторые неорганические и соединения, например соединения типа AIIIBV , в состав которых входят элементы III и V групп периодической соотношении 1: 1. системы мольном

Квантовомеханическое описание твердого тела • Образование связи в молекулах • Согласно принципам квантовой теори, электрон в атоме обладает рядом дискретных энергетических уровней.

• Решениями уравнения Шредингера являются волновые функции, которые тесно связаны с вероятностью электронной нахождения плотностью) электрона в (или данной точке пространства. Этим функциям, или электронным орбиталям, дискретные соответствуют значения определенные доступных энергий, зависящие от величины квантовых чисел

• Все остальные значения энергии запрещены. • Согласно принципу Паули, два электрона одновременно не могут находится в одном и том же квантовом состоянии. Каждое состояние, описываемое первыми тремя квантовыми числами, может быть занято не более чем двумя электронами с антипараллельными спинами.

• Принцип Паули лежит в основе многих теорий и имеет большое значение для объяснения фундаментальных свойств твердого тела. • На рис. 11 показано строение электронного облака (или распределение электронной плотности) для трех низших азимутальных состояний s, p и d, каждому из которых соответствуют два дозволеных спиновых состояния.

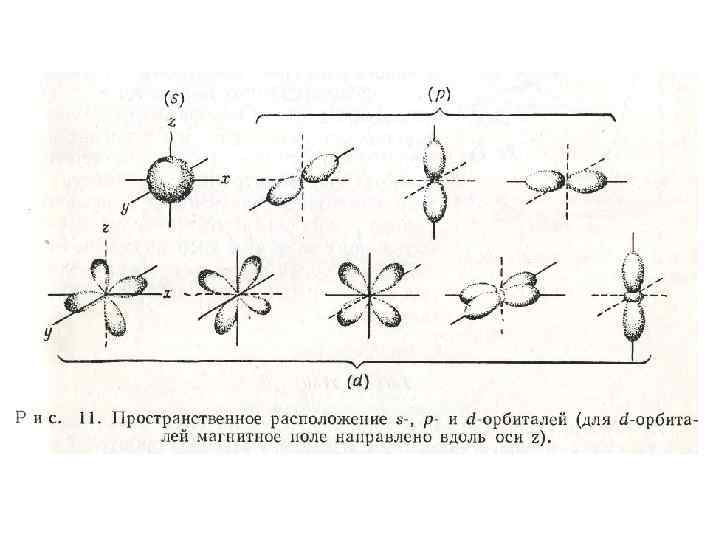
• В s-состоянии электронное облако обладает сферической симметрией, а в p-состоянии оно имеет осевую симметрию относительно одной из трех главных осей в соответствии с тремя возможными значениями магнитного квантового числа. Электронное облако в d-состоянии может иметь пять различных конфигураций.

• Это соответствует пяти возможным значениям магнитного квантового числа, т. е. пяти возможным квантовым состояниям. В трех из них ветви, расположенные в плоскости xy, xz или yz, направлены под углом 450 к главным осям. В одном состоянии четыре ветви расположены вдоль осей x и y и еще в одном состоянии две ветви вытянуты вдоль оси z.

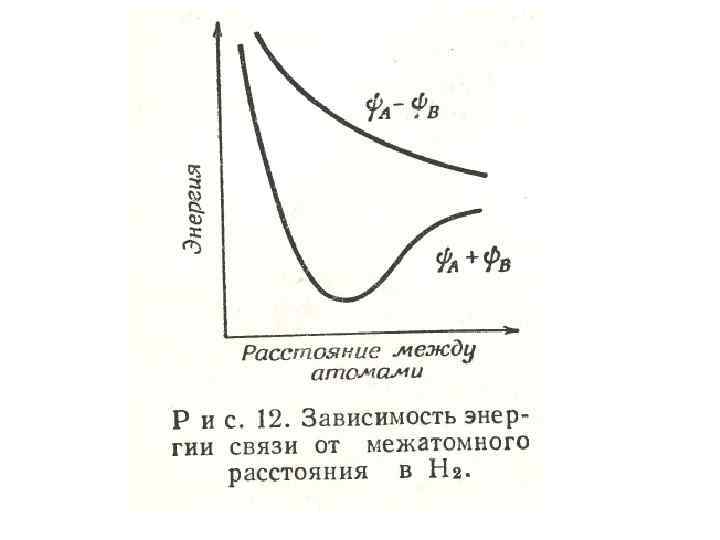
• Электронные волновые функции (орбитали) молекулы образуются из волновых функций отдельных атомов. Если сблизить атомы водорода HА HВ так чтобы волновые функции их 1 s-электронов перекрывались, то волновые функции молекулы водорода можно выразить как А + В или А - В.

• Первая из этих молекулярных орбиталей соответствует системе с меньшей энергией, электроны часть времени находятся между атомами, в поле притяжения обоих атомов, что обуславливает энергии связи. положительное значение

• Волновой функции А - В соответствует минимальная электронная плотность между атомами, обращаясь в нуль посредине линии связи, что приводит значению энергии связи. к отрицательному

Твердое тело • Рассмотрим изменение атомных орбиталей при взаимодействии шести атомов водорода, расположенных линейно. С уменьшением расстояния между атомами водорода, атомные уровни (рис. 13) начинают расщепляться на зоны, дозволенные для 1 s-, 2 s- и т. д. уровней.

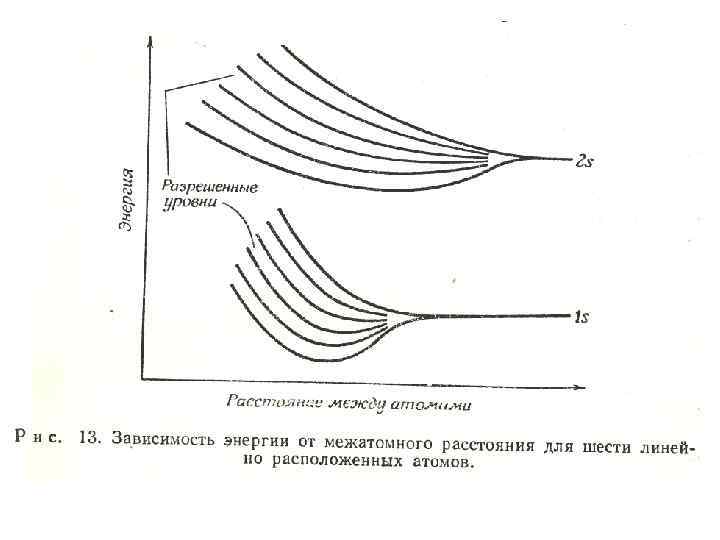
• Каждая зона содержит шесть уровней для каждого из трех первых квантовых чисел (а с учетом спина - 12), поскольку все шесть атомов водорода расположены линейно. Ширина зоны зависит от степени взаимодействия. С увеличение числа взаимодействующих атомов увеличивается число уровней в зоне.

• Ширина же зоны остается неизменной при заданном межатомном расстоянии. Поэтому уровни в зоне сближаются, хотя они всегда остаются дискретными. В соответствии с принципом Паули число электронов, которые могут разместиться в каждой зоне, равно удвоенному числу уровней.

• В реальных твердых телах, где плотность атомов составляет 1023 см-3, число уровней в зоне имеет такой же порядок, а расстояние межу уровнями очень мало, но сохраняется некоторое расстояние между разными зонами.

• Таким образом, при переходе от атомов и молекул к твердому телу дискретные энергетические уровни заменяются зонами, состоящими из большого числа дискретных уровней, но расстояние между зонами может оставаться значительным.

• Приведенное качественное описание электронных энергетических состояний в твердом теле основано на предположении об образовании более или менее прочной связи. Это предположение лежит в основе метода, называемого “приближением сильной связи”. Это представление более справедливо для электронов внутренних оболочек.

Приближение, основанное на модели свободных электронов • Согласно этому приближению валентные электроны свободно двигаются по всему объему металла и ионы металла погружены в этот электронный применимо объясняет газ. к Это приближение одновалентным такие их хорошо металлам свойства электропроводность и поглощение света. и как

• Но оно не объясняло изменения теплоемкости, магнитной восприимчивости и факта существования диэлектриков. • Одним из важнейших выводов метода, основанного на модели свободных электронов, является определение электропроводности: • = Nq 2 /m (2. 1)

• N – концентрация электронов проводимости, q и m – заряд и масса электрона, - время релаксации, которое связано со средним временем между двумя последовательными столкновениями, т. е. свободного пробега. со средней длиной

• Величина перенесенного заряда должна быть пропорциональна: а) плотности носителей тока Nq, б) времени релаксации, т. к. оно характеризует время, в течение которого поле воздействует на электрон, до следующего столкновения с решеткой, в) величине q/m, поскольку ускорение электрона в поле прямо пропорционально заряду и пропорционально массе электрона. обратно

• Теория свободного электрона не объясняет высоких значений длины свободного пробега электрона, которая в металлах при комнатной температуре равна 100 А, что соответствует 10 -14 с. • Величина q/m в уравнении (2. 1) оппределяется как подвижность , т. е. средняя скорость движения электрона в поле единичной напряженности

• Если в уравнении 2. 1 провести соответствующую замену, то • = q. N , • т. е. электропроводность равна произведению концентрации носителей на величину заряда и подвижность носителей в электрическом поле. • Другие параметры, например теплопроводность за счет электронов проводимости, можно также рассчитать в приближении свободных электронов, но только с использованием законов классической механики.

• Согласно этой теории можно ожидать, что электроны проводимости теплоемкость валентных дадут равный 3 RZ/2 электронов в (Z атоме. вклад – в число Однако экспериментально найденные значения вклада электронов проводимости в величину удельной теплоемкости металлов оказались много меньше рассчитанных.

• Аналогичное различие между рассчитанными и экспериментально найденными значениями обнаружено и для магнитной восприимчивости. • Для устранения указанных недостатков Зоммерфельд модифицировал модель свободных электронов на основе представлений квантовой механики

• Решением свободного уравнения электрона Шредингера является для волновая функция вида • = eikr • k – произвольный вектор. Волновое число k связано с длиной волны электрона соотношением k = 2 /

• Налагая условие периодичности решетки, например для куба со стороной L: • (x + L, y, z) = (x, y, z) • И соответствующие уравнения для y и z. Решение, удовлетворяющее этому уравнению • ≈ exp[i 2 /L(nxx + nyy + nzz)] • ni – положительное или отрицательное целое число

• Это решение удовлетворяет периодичности, так как e 2 i≡ 1. условию Следовательно вектор k может принимать значения, определяемые выражением • k=n

• n 2 = nx 2 + ny 2 + nz 2 Энергия свободного электрона определяется как E = p 2/2 m, p – импульс электрона. По соотношению де-Бройля P = bk, так что (2. 7),

• В модифицированной модели свободного электрона энергия электрона дается уравнением (2. 7), но дозволенные значения k определяются уравнением (2. 6). Каждому допустимому значению k соответствуют два электронных состояния с антипараллельными спинами. Суммированием по всем возможным значениям n можно определить число дозволенных состояний как функцию энергии.

• Заполнение состояний электронами показано на рис. 14 (заштрихованный участок). Каждому значению k, согласно принципу Паули, соответствуют два электрона (со спинами ± 1/2). Заполнение электронов начинается с самых низших разрешенных уровней и продолжается до тех пор, пока не будут использованы все валентные электроны.

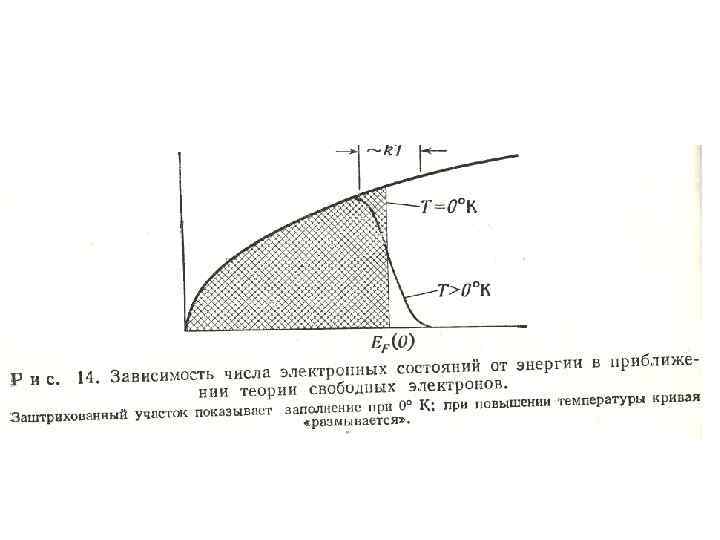
• Для одновалентных металлов число таких электронов равно одному на каждый атом. Заполнение состояний характеризуется значениями электронами энергии, называемым уровнем Ферми. При абсолютном нуле все состояния, расположенные ниже уровня Ферми, заполнены, состояния свободны. а все вышележащие

• С повышением температуры вследствие теплового возбуждения часть электронов переходит из состояний, лежащих ниже уровня Ферми, в состояния с энергией, превышающей уровень Ферми (показано тонкой кривой рис. 14), что приводит к размыванию первоначальной функции распределения состояний и как результат – к небольшому сдвигу уровня Ферми при увеличении температуры.

• Изложенная свободных квантовомеханическая электронов экспериментальным дает более значения теория близкие величины к вклада электронов проводимости в теплоемкость металлов. Причину этого нетрудно понять с помощью рис. 14. Изменение внутренней энергии при нагревании твердого тела определяется разностью полной энергии для распределения при двух температурах.

• Эта разность электронами, обусловлена энергия лишь которых теми близка к значению ЕF. Так, нагревание металла от 00 К до Т 0 К приводит лишь к увеличению внутренней энергии электронов за счет перехода сравнительно малого числа электронов из состояния с энергией ниже ЕF в состояние с энергией выше ЕF

• Аналогичный подход используется при рассмотрении данных по магнитной восприимчивости металлов. Изменить спин в приложенном магнитном поле могут лишь некоторые из электроны с энергией, близкой к ЕF, так как почти все состояния с Е < ЕF заняты и в каждом из них, по принципу Паули, находятся по два электрона с антипараллельными спинами.

• Поэтому следует ожидать, что только очень небольшая доля электронов будет вносить вклад в магнитную восприимчивость. Этот вывод подтверждается экспериментальными данными.

Зонная теория • Мы рассмотрели электронное строение твердого тела для двух простейших случаев: в приближении свободного приближении сильной электрона связи при и в малом перекрывании волновых функций. Каждое из приближений имеет свои достоинства и свои области применимости.

• Современная теория электронного строения твердого тела основана на более строгом решении уравнения Шредингера с учетом периодического потенциала, обусловленного атомами решетки. Такое решение, найденное Блохом, имеет вид: • k = eikxuk(x) • k - волновое число (2. 8)

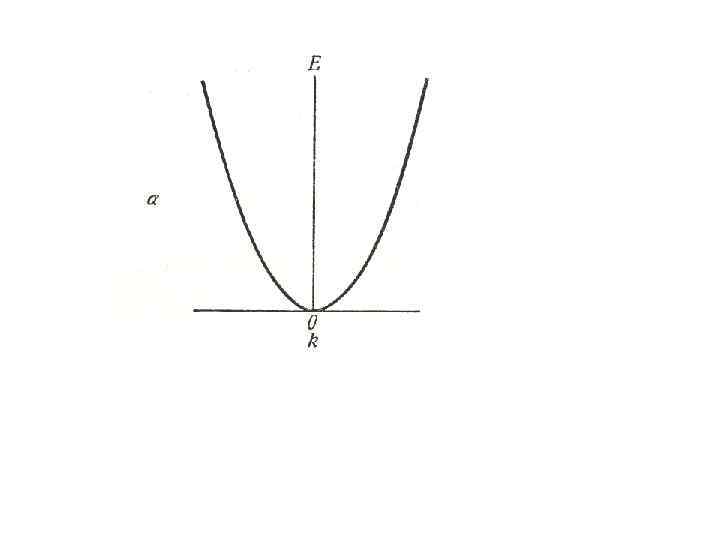
• u(x) – периодическая функция с периодом, равным постоянной решетки а, в общем виде функция uk(x) зависит от k. • Квадратичная зависимость энергии волнового числа, полученная в приближении свободного электрона, представлена на рис. 15 а.

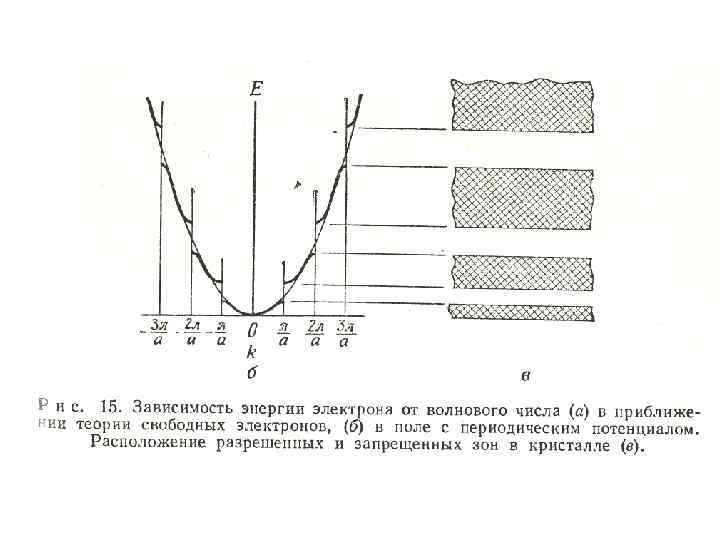
• На рис. 15 б представлена та же зависимость для периодического потенциального поля. При k, равном /a, 2 /a, 3 /a и т. д. , энергия претерпевает разрыв, т. е. имеются разрешенные и запрещенные уровни энергии, что соответствует рассмотренной ранее картине взаимодействующих атомов.

• Разрывы энергии можно понять так. Решением волнового уравнения в приближении свободного электрона является уравнение плоской волны, имеющей в одномерном пространстве вид eikx. В периодическом поле с периодом, равным постоянной решетки а, решение не может быть представлено в столь простом виде.

• Для большинства значений волнового числа k электроны рассматриваются как свободные и хорошо описываются уравнением плоской волны. При значениях k = ± /a, 2 /a и т. д. электроны находятся в условиях Брэгговского отражения, поскольку выражение k = n /a эквивалентно уравнению Брэгга 2 аsin = n , так как k = 2 / , а sin = 1.

• Поэтому k ≈ n/a соответствует увеличенным значениям компоненты отраженной волны в решении волнового уравнения. • При значениях k, заметно отличающихся от ± /a, 2 /a и т. д. , энергия электрона хорошо описывается квадратичной от k для свободного электрона, в которой используется истинная масса электрона.

• При значениях k близких к n/a для описания энергии электрона эта зависимость не может быть использована вследствие обмена импульсами между электронами и решеткой. Но если заменить истинную массу электрона на так называемую эффективную массу, то квадратичная зависимость энергии от волнового числа может иметь место

• С учетом эффективной массы (m*) • Ek = (h 2/2 m*)k 2 • где m* изменяется в зависимости от k. Это уравнение хорошо описывает зависимость ускорения электронов с различным значением k от напряженности электрического поля.

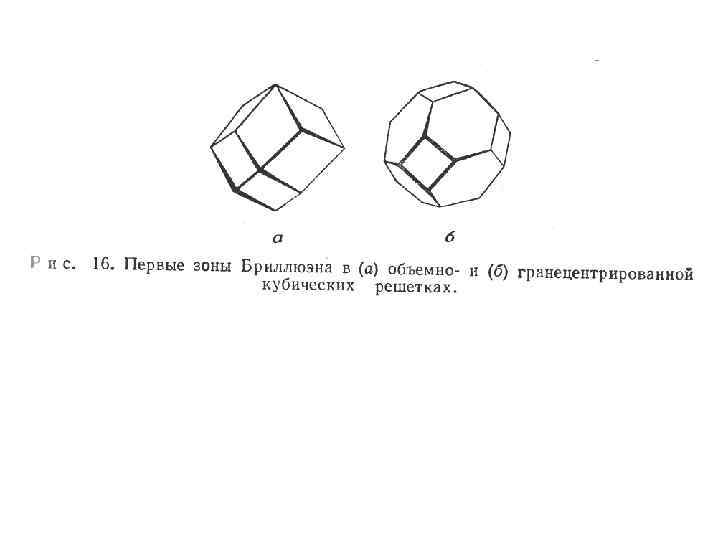
• Области, ограниченные целочисленными значениями /a, называются зонами Бриллюэна. На границах зон наблюдаются разрывы значений энергии. Первая зона включает отрезок - /a < k < + /a, вторая зона включает два отрезка - 2 /a < k < - /a и /a < k < 2 /a и т. д. Аналогично рассматривается реальный трехмерный кристалл. (рис. 16)

• Обычно разрешенные и запрещенные уровни изображают, располагая их в виде полос на вертикальной шкале, а горизонтальная ось показывает расстояние внутри кристалла.

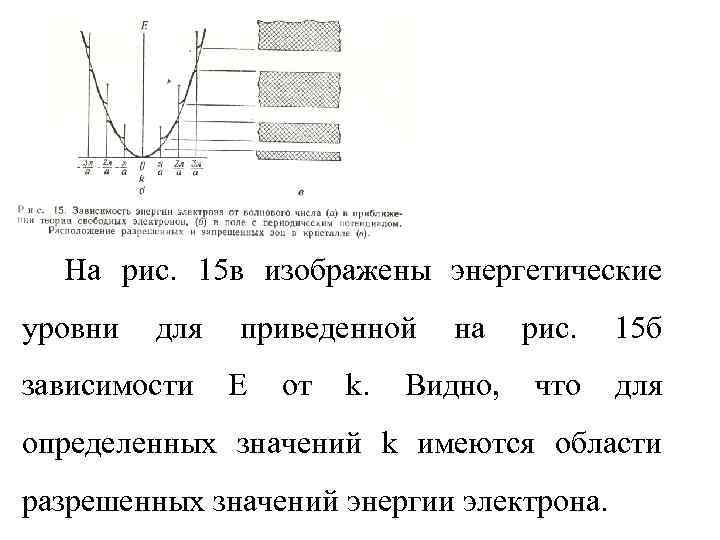На рис. 15 в изображены энергетические уровни для зависимости приведенной E от k. на Видно, рис. 15 б что для определенных значений k имеются области разрешенных значений энергии электрона.

• Электроны последовательно заполняют все разрешенные уровни, начиная с наинизшего. Самая верхняя зона может быть полностью или частично заполнена валентными электронами в зависимости от природы атомов в твердом теле. • На рис. 17 представлены эквиэнергетические поверхности для двумерной кубической решетки в К-пространстве.

• Внутренние поверхности имеют вид почти правильных окружностей, а верхние поверхности искажаются вблизи края зоны. На рис. 17 показаны два низших уровня следующей зоны, они не являются вследствие поверхности непрерывности продолжением нарушения энергии, запрещенной зоны. соответствующей

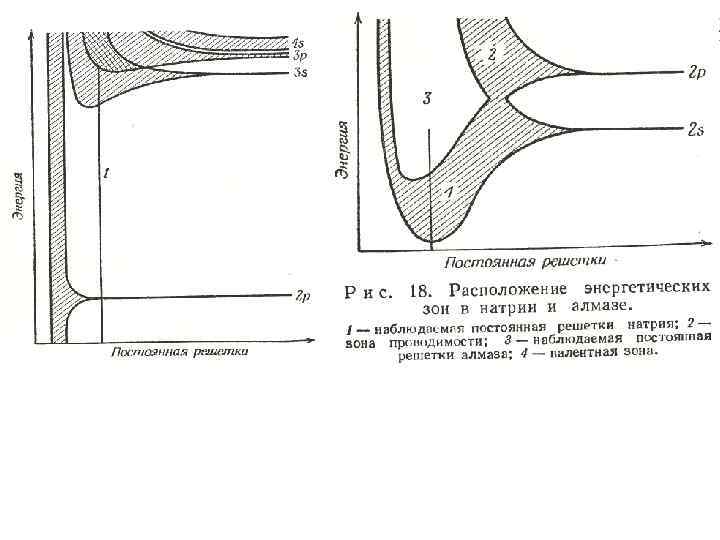
• На рис. 18 показано расположение энергетических зон в натрии и алмазе. При равновесном межатомном расстоянии зоны с низшей энергией узкие и отделены друг от друга. Зоны высокой энергии шире и здесь уже происходит перекрывание. Нижние зоны можно приписать той или иной атомной орбитали, для внешних уровней это сделать нельзя. Смешение атомных орбиталей равносильно гибридизации в молекулярных системах.

Закон распределения электронов по энергетическим состояниям • Согласно закону Паули, в данном состоянии (с учетом спина) может находится лишь один электрон. Рассмотрим заполнение электронами разрешенных состояний. При 00 К заняты лишь низшие уровни, но с повышением температуры распределение сглаживается (рис. 14).

• Количественно распределение электронов описывается статистикой Ферми-Дирака. Статистика Ферми-Дирака применяется к электронам как к системе неразличимых частиц, каждая из которых может находится лишь в одном состоянии.

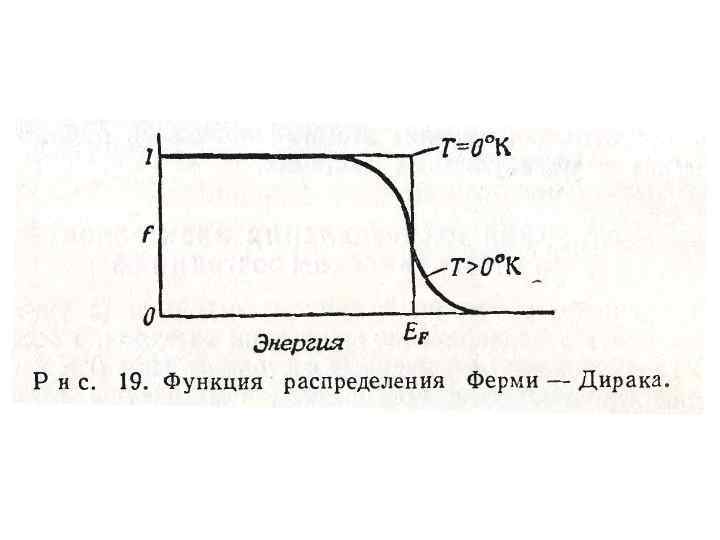
• Функция определяющая распределения вероятность Ферми-Дирака, того, что данное состояние занято, имеет вид: E – энергия данного состояния, EF - уровень Ферми. При Т = 00 К, f = 1 для всех значений E « EF и f = 0 при E » EF. Если T>00 K, f≈1 для всех значений E

• На рис. 19 показаны зависимость f от Е при Т = 00 К и Т > 00 К. Видно, что значения функции, соответствующие занятым состояниям (заштрихованная область) получены простым умножением плотности состояний на функцию распределения температуры. Ферми-Дирака для данной

• При (E – EF) » k. T, т. е. в хвостовой части распределения электронов по энергии, функция распределения приближенно приобретает следующий вид что соответствует классической распределения Больцмана функции

Уровень потенциал Ферми – это электронов, химический или их парциальная мольная свободная энергия

Диэлектрики, полупроводники, металлы • Электронную структуру металлов, полупроводников и многих других твердых тел можно описать в рамках зонной теории.

• Если все энергетические зоны твердого тела, в которых имеются электроны, полностью заполнены, то такое твердое тело называют диэлектриком. • Если же верхняя зона заполнена примерно наполовину, вещество относится к классу металлов

• В промежуточном слое, когда верхняя зона, содержащая электроны, концентрацию состояний, пустых вещество имеет или относят малую заполненных к классу полупроводников. На рис. 20 схематически представлены все три случая

• Электрическое поле не может ускорить электроны полностью заполненной зоны и, следовательно, вследствие изменить принципа их Паули. k-векторы, И большого расстояния между разрешенными зонами

• При частичном заполнении зоны принцип Паули уже не препятствует приобрести дополнительную энергию и электрическое поле способно увеличить компоненту волнового вектора k, направленную вдоль поля (рис. 21)

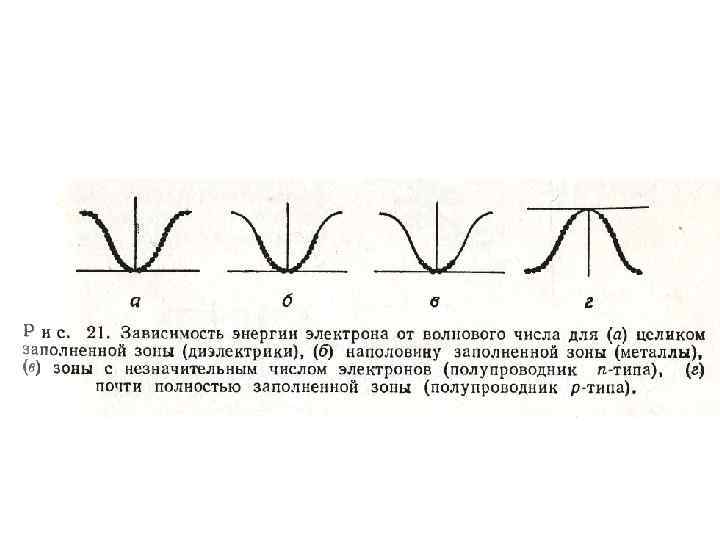
• В металлах число таких электронов, способных проводить ток примерно равно числу атомов твердого тела. • В полупроводниках электроны также могут двигаться, но число этих электронов (или число незанятых состояний в почти заполненной зоне) меньше на несколько порядков числа атомов.

• Такое передвижение электронов можно уподобить движению машин в гараже. На этаже, полностью заполненном машинами, они двигаться не могут. В наполовину способных заполненном двигаться в этаже, заданном число машин, направлении, максимально. Наличие одной или двух машин на этаже, или наоборот, наличие лишь нескольких свободных мест не может привести к значительному потоку машин в заданном направлении.

• Полупроводники электронов в с зоне небольшим относят к числом n-типу, а полупроводники с небольшим числом вакансий в зоне (дырок) различие – в к р-типу. Незначительное электронной структуре полупроводников и диэлектриков приводит к значительному различию в их электрических свойствах.

Запрещенные зоны • В диэлектриках ширина запрещенной зоны достигает нескольких электрон-вольт. Если ширина запрещенной зоны мала, тепловой энергии достаточно, чтобы перенести некоторое число электронов из валентной зоны в низшую незаполненную зону (зону проводимости) и вещество станет полупроводником.

• Ширина запрещенной зоны зависит от электроотрицательности составляющих вещество атомов. На рис. 22 экспериментально найденная представлены для ряда элементов и соединений зависимость ширины запрещенной зоны электроотрицательности. от величины

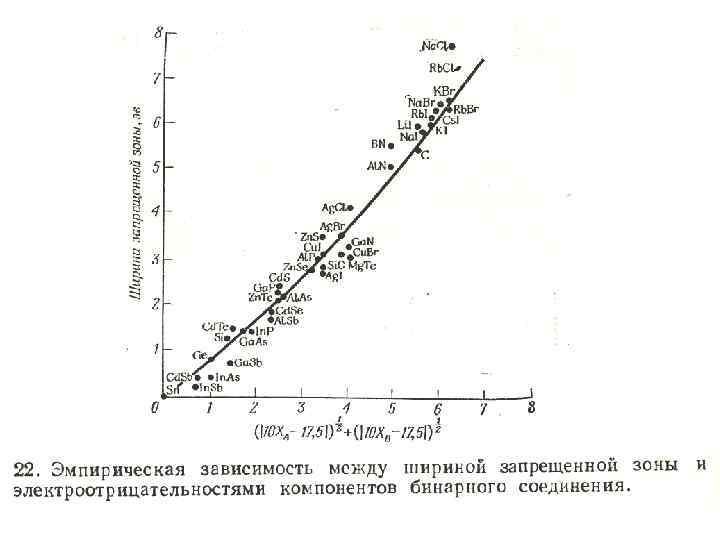
• На рис. 22 приведена экспериментально найденная зависимость ширины запрещенной зоны от величины электроотрицательности для ряда элементов и соединений.

Энергетические зоны • Различие в свойствах металлов разных групп периодической таблицы можно описать с помощью зонной теории. Щелочные металлы имеют единственный валентный s-электрон на атом; в совокупности электроны заполняют лишь половину состояний в полосе вследствие двух возможных ориентаций спина электрона.

• Это хорошо соответствует приближению свободных электронов со сферически симметричной поверхностью Ферми. • Двухвалентные щелочноземельные металлы обладают двумя валентными электронами на атом, которые заполняют внешнюю s-зону; так что щелочноземельные металлы были бы диэлектриками, если бы не перекрывание s-зоны с лежащими выше незаполненными p- и d-зонами.

• Cu, Ag, Au одновалентны, но отличаются от щелочных металлов тем, что имеют заполненную d-зону, перекрывающуюся с sзоной. Поэтому d-электрон также может принимать участие в образовании химической связи.

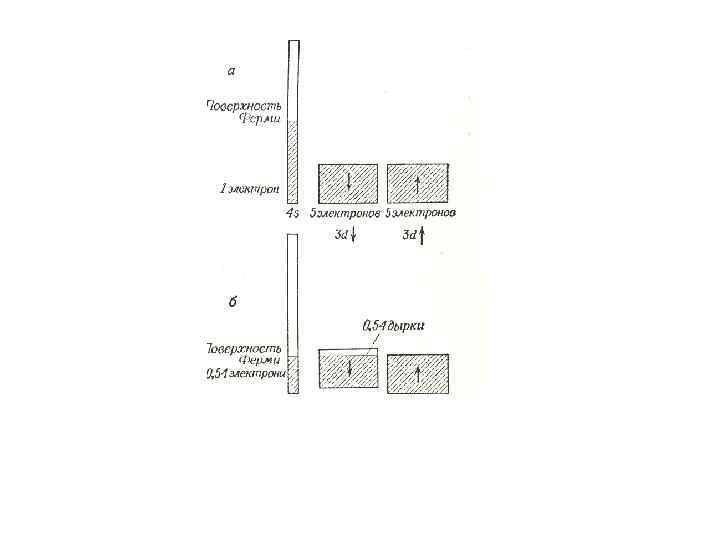
• В переходных металлах d-зона лишь частично заполнена и перекрывается с лежащей выше соседней s-зоной, которая без перекрывания была бы не заполнена. Магнитные свойства таких металлов определяются их зонной структурой. Например медь имеет целиком заполненную содержит 10 электронов 3 d-зону, которая

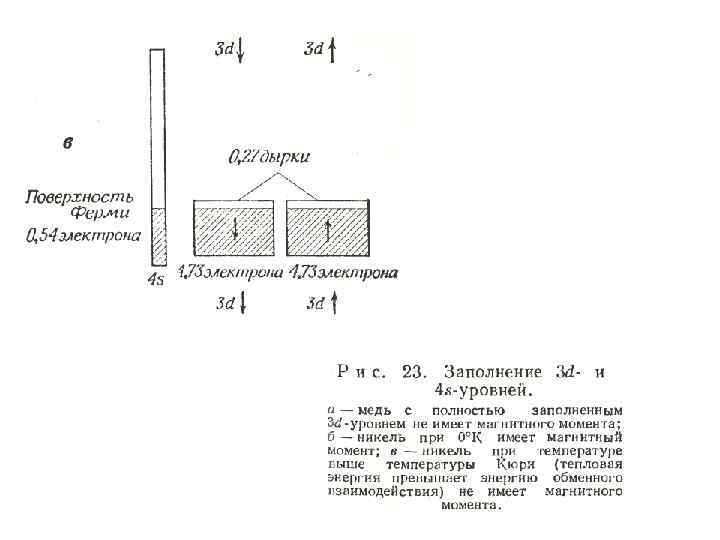
Половина этих электронов имеет спины, направленные вверх, а вторая половина – вниз. Кроме того, в этой зоне есть один 4 s-электрон. У атома никеля на один электрон меньше, и вследствие перекрывания 4 s- и 3 d-зон и перехода части 3 d-электронов в 4 s-зону у каждого атома в 3 d-зоне не достает примерно 0, 54 электрона

• В результате так называемого обменного взаимодействия в 3 d-зоне имеется избыток электронов с одним направлением спина (расщепление 3 d-зоны), что приводит к определенной появлению ферромагнетизма. температуры (температура Выше Кюри) тепловая энергия электронов нарушает слабое обменное взаимодействие. В результате чего все электроны спарены, т. е. распределяются поровну между двумя возможными спиновыми состояниями.

• Сжимаемость Cu, Ag, Au и переходных металлов много меньше, чем у щелочных, поскольку полностью или частично заполненные d-оболочки перекрываются или касаются друга, что препятствует проникновению орбиталей. взаимному

Бинарные сплавы • Зонная теория твердого тела объясняет также эмпирическое правило Юм-Розери, касающееся свойств бинарных сплавов, которые образуют твердые растворы путем беспорядочного распределения атомов двух видов. Согласно этим правилам растворы замещения образуются только при выполнении некоторых условий.

• К этим условиям относятся соответствие атомных размеров, кристаллических структур, электроотрицательности, валентности и др. . • Если сплав образует несколько модификаций, имеющих различные кристаллические структуры (например сплав меди и цинка), то переходы между фазами соответствуют определенному постоянному соотношению числа валентных составляющих сплав атомов. электронов и

• Согласно зонной теории, это можно объяснить тем, что в точках определенного состава поверхность Ферми касается границы зоны Бриддюэна, поскольку введение дополнительных электронов за пределы зоны требует сравнительно большой затраты энергии. Процесс повторяется при других составах, соответствующих следующему фазовому переходу.

Теория поля лигандов • Некоторые свойства ионных кристаллов – соединений металлов с частично заполненными 3 d-оболочками, хорошо объясняются в рамках теории поля лигандов. Согласно этой теории, химическая связь в кристаллах соединений металлов является чисто ионной

• Ионы заряды, рассматриваются а их как точечные поле симметрией!) несферической электрическое (с вызывает расщепление 3 d-уровня иона металла. Теорию поля лигандов объяснения можно строения использовать как для комплексных соединений, так и различных твердых веществ.

• Для учета точечного отклонения заряда вводится от простого параметры, включающие степень ковалентности связи, поляризационное искажение за счет соседних зарядов, величину отклонения от сферической симметриеи ионов с частично заполненными dорбиталями.

• С помощью теории групп модно объяснить и предсказать расщепление атомных уровней, соответствующее тому или иному типу симметрии внутреннего электронного поля в кристалле. • Так, ион Ti+3 c единственным d-электроном находится в октаэдрическом окружении восьми анионов, расположенных по осям x, y и z.

• Пять d-орбиталей, вырожденных в отсутствие окружающих групп, расщепляются в кристаллическом поле вследствие того, что электрон на d-орбиталях, вытянутых вдоль осей ( ) испытывает отталкивание близлежащих к нему электронов, что повышает электронную энергию этих орбиталей по сравнению со свободным ионом.

• Энергия трех остальные d-орбиталей, не лежащих вдоль увеличивается осе в (dxy, меньшей dyz и dxz) степени, что приводит к расщеплению d-уровней. Величина этого расщепления обозначается как 10 Dq и находится поглощения. и з оптических спектров

• Теория поля лигандов имеет большое значение для понимания сложных оптических спектров соединений металлов с частично заполненной d-оболочкой. Как правило эти соединения окрашены. Окраска вещества обусловлена электронными переходами между нижним и верхним d-уровнями, так как величина 10 Dq соответствует длине волны электромагнитного спектра. видимой части

• Теория объясняет магнитные свойства этих соединений. Например Co 3 O 4. В зависимости от расположения в кристаллической решетке ионы кобальта двух- или трехвалентны и формула соединения Co 2 IIICo. IIO 4.

• Если бы d-уровни были полностью вырожденными, как в свободном ионе, на одну молекулу соединения приходилось бы 11 неспаренных электронов, так как согласно принципу Гунда, конфигурация d 6 и в Co+3, в Co+2, электронная конфигурация d 7, расположение спинов имеет соответственно такой вид: и

• При ситуация сильном расщеплении меняется. Окружение d-уровня иона Co+3 расщепляет d-уровень на три нижних и два верхних уровня. Четыре из семи d-электронов заполняют попарно оставшиеся три два нижних электрона уровня, заполняют три верхних уровня (по одному на каждом уровне), так что их спины параллельны.

• Таким образом, благодаря наличию трех неспаренных электронов показывает Co 3 O 4, эксперимент, как проявляет результирующую намагниченность. • Теория поля лигандов объясняет химические особенности указанных веществ.

• Например, нарушение непрерывности размера ионного радиуса катионов в ряду металлов с недостроенной 3 d-оболочкой в точках, где электроны имеют орбитали, направленные в сторону лигандов, можно объяснить избыточным отталкиванием, размера катиона. приводящим к увеличению

• Поле лигандов влияет также на энергию решетки кристалла. Различная стабильность кристаллических катионами с решеток, частично построенных заполненными d- оболочками, объясняется разным соотношением между типом симметрии, расщеплением d-уровня и степенью его заполнения

• Например, известно, что в шпинели Fe 3 O 4 октаэдрические положения заняты Fe+2, в то время как в Mn 3 O 4 они заняты трехвалентными ионами. Согласно теории поля лигандов это объясняется тем, что октаэдрическое кристаллическое поле (анионов) стабилизирует Fe+2 и Mn+3 и не стабилизирует Fe+3 и Mn+2