Электронное строение кристаллов Лекция 3 Классификация по

Электронное строение кристаллов Лекция 3

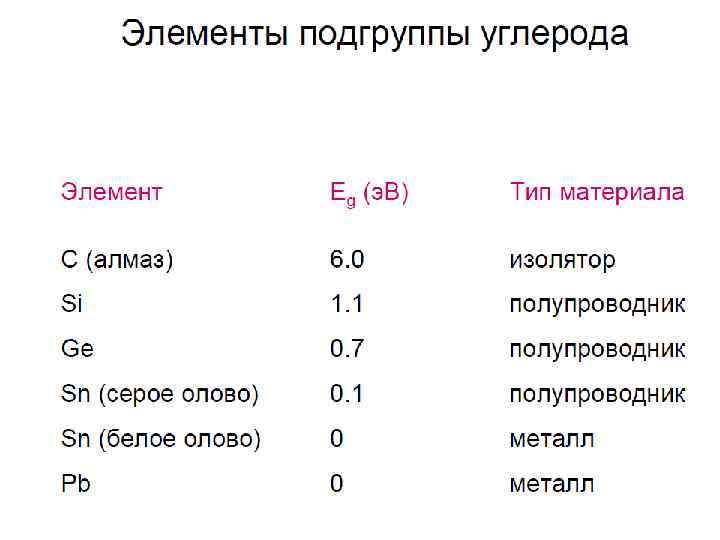
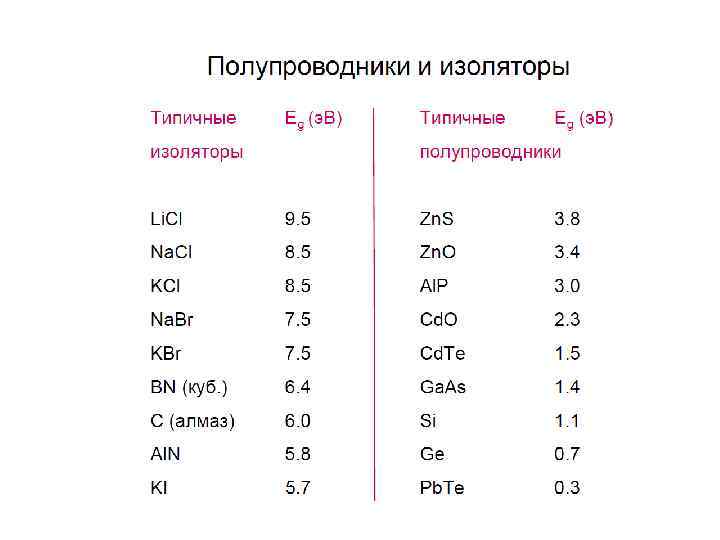
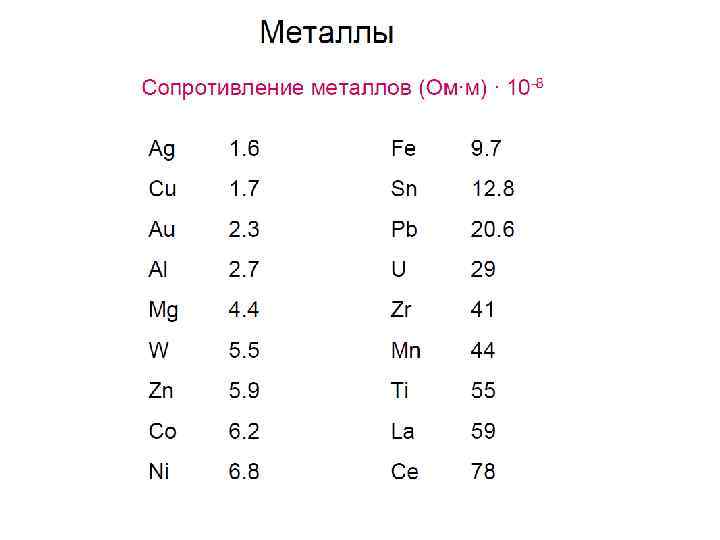
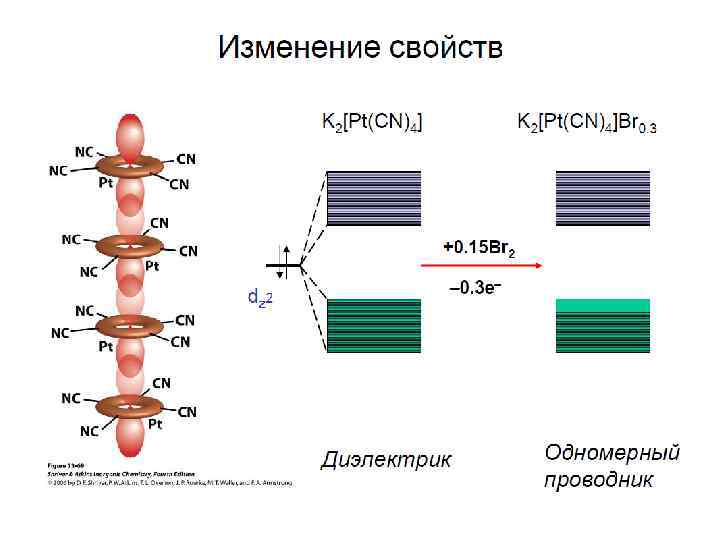
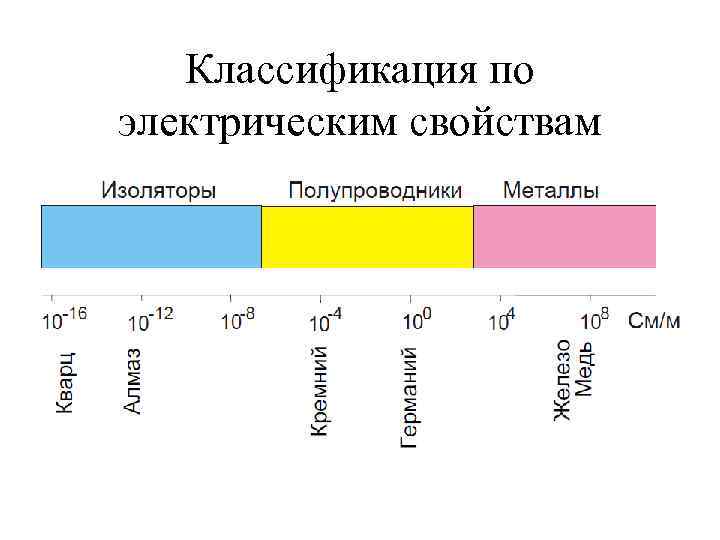Классификация по электрическим свойствам

Обратная решетка T = ua + vb + wc прямая решетка Направляющие вектора обратной решетки: k – волновой вектор в пространстве обратной решетки (фазовое пространство) Формула де Бройля для электрона =h/p=h/(m v) Импульс электрона в вакууме: p=ħ k Энергия свободного электрона: E= ħ 2 k 2/(2 m)

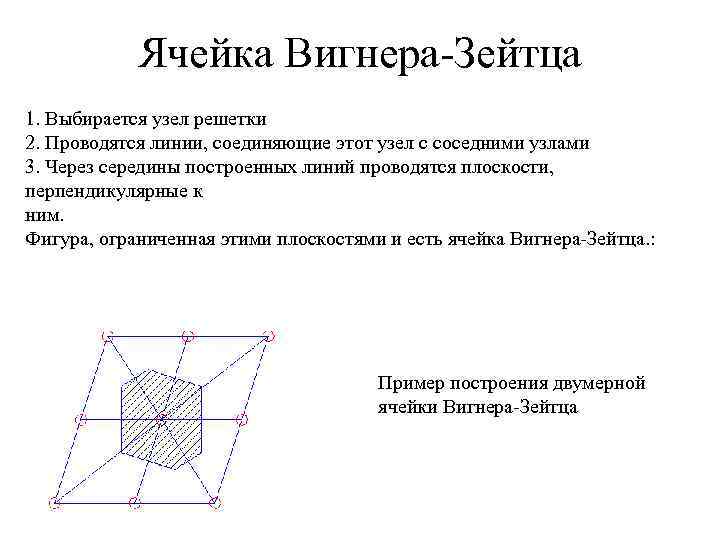Ячейка Вигнера-Зейтца 1. Выбирается узел решетки 2. Проводятся линии, соединяющие этот узел с соседними узлами 3. Через середины построенных линий проводятся плоскости, перпендикулярные к ним. Фигура, ограниченная этими плоскостями и есть ячейка Вигнера-Зейтца. : Пример построения двумерной ячейки Вигнера-Зейтца

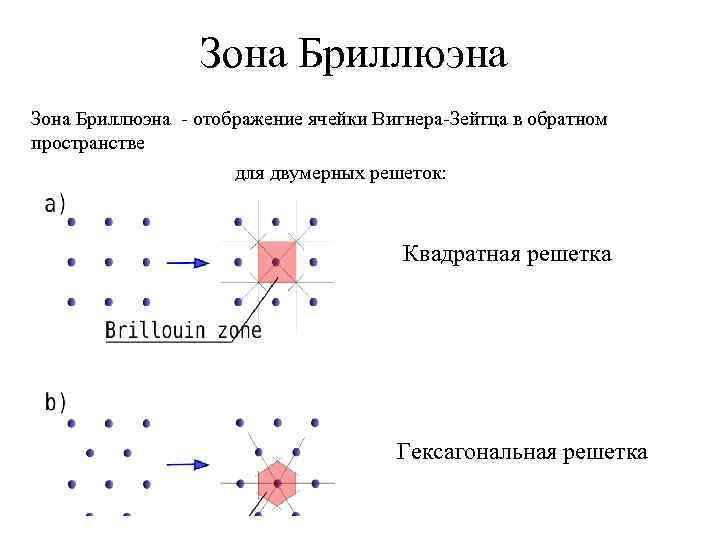Зона Бриллюэна - отображение ячейки Вигнера-Зейтца в обратном пространстве для двумерных решеток: Квадратная решетка Гексагональная решетка

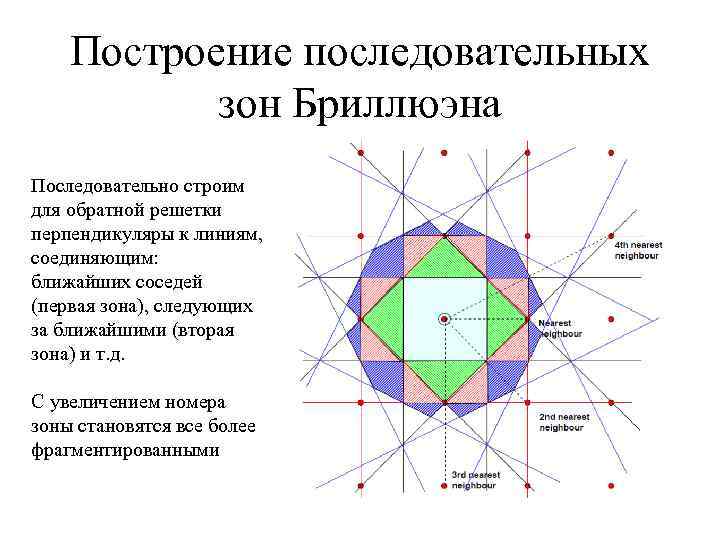Построение последовательных зон Бриллюэна Последовательно строим для обратной решетки перпендикуляры к линиям, соединяющим: ближайших соседей (первая зона), следующих за ближайшими (вторая зона) и т. д. С увеличением номера зоны становятся все более фрагментированными

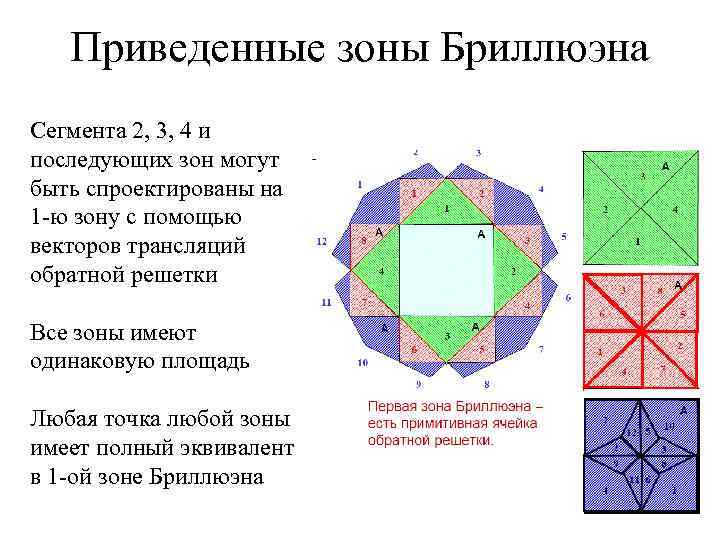Приведенные зоны Бриллюэна Сегмента 2, 3, 4 и последующих зон могут быть спроектированы на 1 -ю зону с помощью векторов трансляций обратной решетки Все зоны имеют одинаковую площадь Любая точка любой зоны имеет полный эквивалент в 1 -ой зоне Бриллюэна

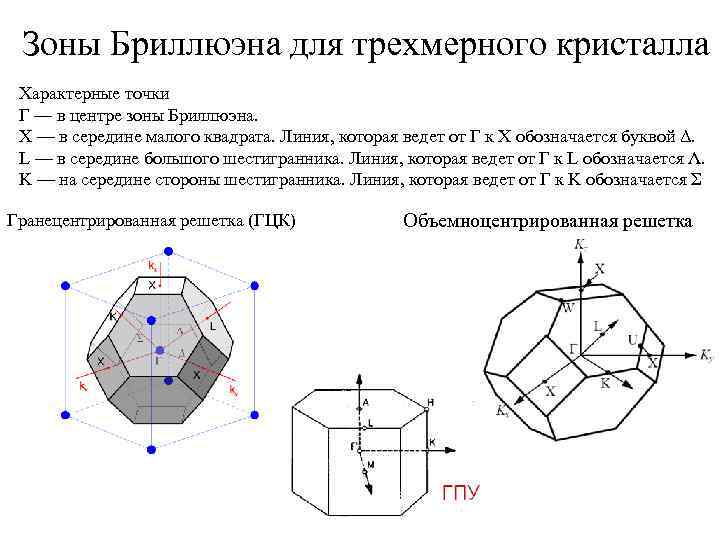Зоны Бриллюэна для трехмерного кристалла Характерные точки Γ — в центре зоны Бриллюэна. X — в середине малого квадрата. Линия, которая ведет от Γ к X обозначается буквой Δ. L — в середине большого шестигранника. Линия, которая ведет от Γ к L обозначается Λ. K — на середине стороны шестигранника. Линия, которая ведет от Γ к K обозначается Σ Гранецентрированная решетка (ГЦК) Объемноцентрированная решетка

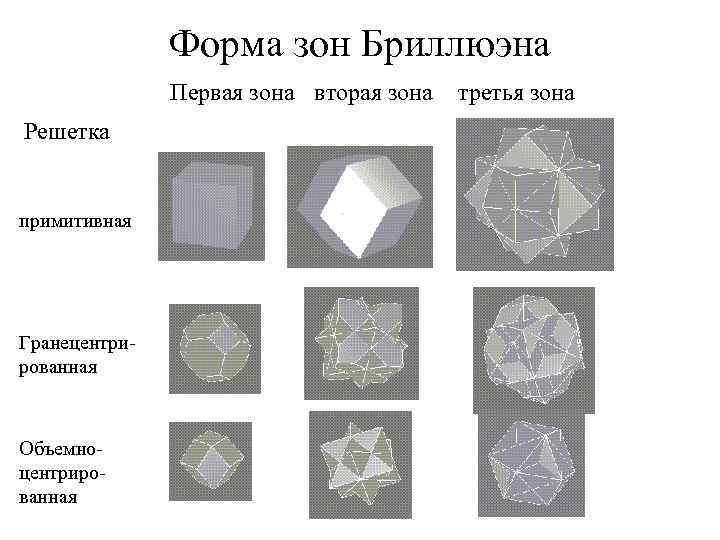Форма зон Бриллюэна Первая зона вторая зона Решетка примитивная Гранецентрированная Объемноцентрированная третья зона

Практическое использование концепции зон Броиллюэна 1) В дифракции излучения: на кристаллической решётке дифрагируют только те лучи, волновой вектор которых оканчивается на границе зоны Бриллюэна. 2) При описании электронной структуры кристалла: вследствие существования периодичности кристаллической решётки и конкретно зоны Бриллюэна в кристалле возникают запрещённые и разрешённые энергетические состояния. Возникновение запрещённых зон связано с тем, что для электронных волн определённых длин на границе зоны Бриллюэна возникает условие брэгговского отражения, и электронная волна отражается от границы зоны.

Общее уравнение Шредингера Плотность вероятности нахождения частицы в точке r в момент времени t:

Стационарное уравнение Шредингера Разделение переменных Стационарное уравнение Шредингера – собственные числа : дискретные уровни энергии – собственные функции n – квантовое число Условие нормировки: Условие ортогональности:

Уравнение Шредингера для водородоподобного атома присоединенный полином Лагерра присоединенный полином Лежандра дискретные уровни энергии

Теорема Блоха Потенциальная энергия электрона в кристалле: U(x)=U(x+a) Псевдомпульс электрона в кристалле: P=ħ k Энергия электрона: E= ħ 2 k 2/(2 m*) m* - эффективная масса электрона, m*=f( k ) n – номер зоны

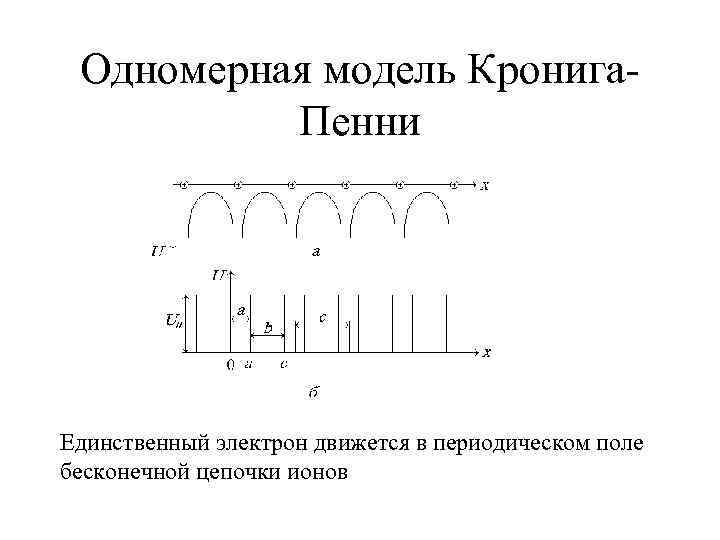Одномерная модель Кронига. Пенни Единственный электрон движется в периодическом поле бесконечной цепочки ионов

Стационарное уравнение Шредингера для модели Кронига-Пенни (1) Начало системы координат (точку х = 0) выберем так, чтобы она совпадала с левым краем потенциальной ямы, Tогда потенциальная функция (2) В соответствии с теоремой Блоха волновая функция электрона y(x) может быть представлена в виде (3) Индексы n и k опущены для простоты записи. Функция u(x) (блоховский множитель) имеет период c Подставляя (3) в уравнение (1), получим дифференциальное уравнение для блоховского множителя (4 а) для электронов, находящихся внутри потенциальных ям, и (4 б) для электронов, находящихся вне потенциальных ям.

Решение уравнения Шредингера для модели Кронига-Пенни Общее решение уравнения (2. 10 а) для электронов внутри потенциальных ям может быть записано в виде , (5 а) a - параметр, который может быть найден подстановкой решения в исходное уравнение (2. 10 а). В области вне потенциальных ям при условии, что высота потенциального барьера U 0 выше полной энергии электрона Е, решение уравнения (2. 10 б) имеет вид , (5 б) Постоянные A, B, C и D в формулах (5 а) и (5 б) находятся как обычно из граничных условий. Граничные условия требуют, чтобы функция u(x) и ее первая производная в местах скачков потенциала, т. е. на стенках потенциальных ям, были непрерывны. Эти требования приводят к следующей системе уравнений: (6)

Решение уравнения Шредингера для модели Кронига-Пенни Определитель системы (6) будет равен нулю (только при этом условии система линейных однородных уравнений имеет отличные от нуля решения), если выполняется следующее равенство: (7) Выражение (7) можно значительно упростить, если допустить, что ширина барьера стремится к нулю b 0 , а его высота - к бесконечности (U 0 ), но таким образом, чтобы произведение оставалось постоянным (U 0 b=const). При этих условиях выражение (7) преобразуется к виду: (8) 1. Слабая связь P 0 (U 0 0) – энергия электрона: - свободный электрон 2. Сильная связь P (U 0 ): => n=1, 2, … - набор дискретных уровней (атом)

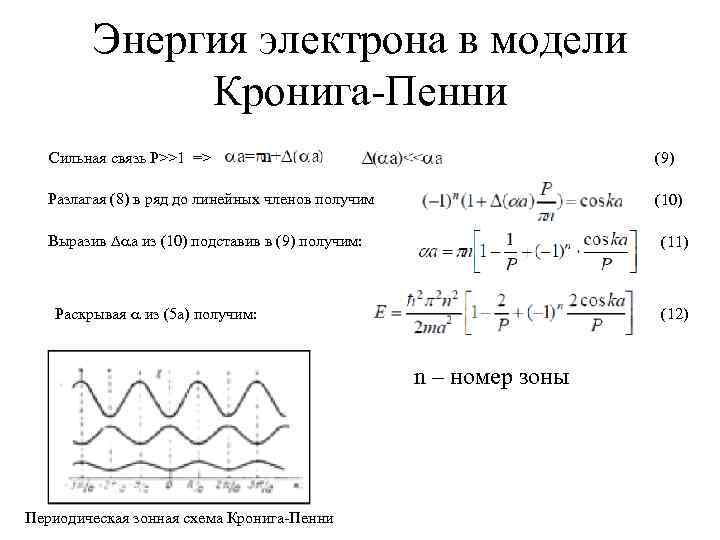Энергия электрона в модели Кронига-Пенни Сильная связь P>>1 => (9) Разлагая (8) в ряд до линейных членов получим (10) Выразив a из (10) подставив в (9) получим: (11) Раскрывая из (5 а) получим: (12) n – номер зоны Периодическая зонная схема Кронига-Пенни

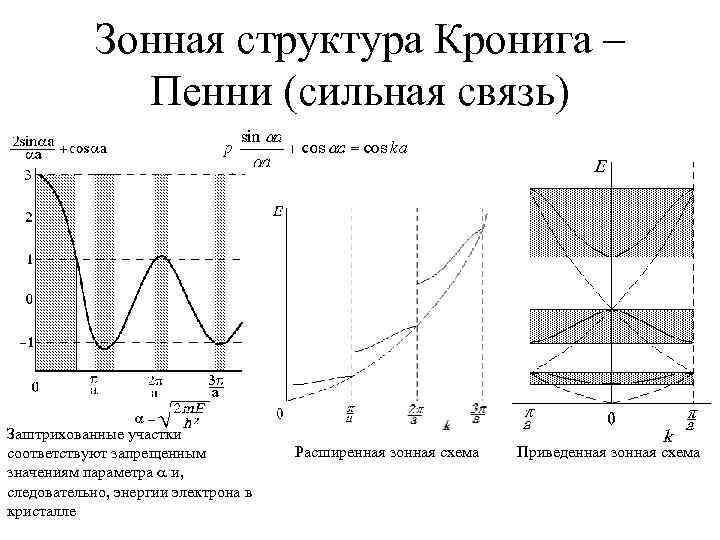Зонная структура Кронига – Пенни (сильная связь) Заштрихованные участки соответствуют запрещенным значениям параметра и, следовательно, энергии электрона в кристалле Расширенная зонная схема Приведенная зонная схема

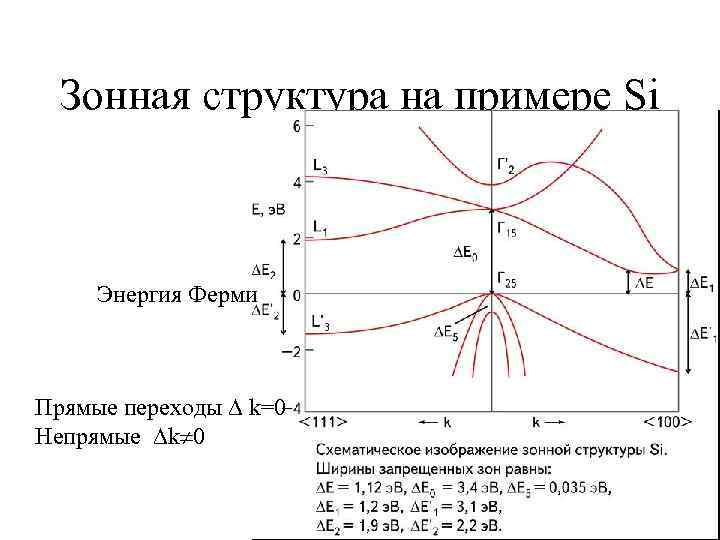Зонная структура на примере Si Энергия Ферми Прямые переходы k=0 Непрямые k 0

Ширина запрещенной зоны щелочно-галоидных кристаллов Кристаллы Фториды Li. F Na. F KF Rb. F Cs. F Бромиды Li. Br Eg, э. В Na. Br 6. 4 – 7. 7 Na. I 5. 8 – 5. 9 KBr 6. 0 – 8. 0 KI 5. 5 – 6. 3 Rb. Br 5. 9 – 7. 3 Rb. I 5. 6 – 6. 4 10. 9 – 14. 5 11. 4 – 12. 7 10. 3 – 11. 1 8. 5 – 10. 3 5. 8 – 10. 0 7. 5 – 8. 4 Кристаллы Eg, э. В Хлориды Li. Cl 7. 7 – 9. 9 Na. Cl 7. 4 – 10. 4 KCl 6. 3 – 9. 6 Rb. Cl 6. 1 – 8. 3 Cs. Cl - Иодиды Li. I 5. 9 – 6. 4

Влияние ограниченного размера кристалла Граничные условия Борна-Кармана: Lx = Nxa , Ly = Nya, Lz = Nza, Ψ(x, y, z) =Ψ(x + Lx, y + Ly , z + Lz ) Разрешенные значения компонентов волнового вектора: Всего в зоне Бриллюэна N разрешенных состояний – квазидискретные состояния:

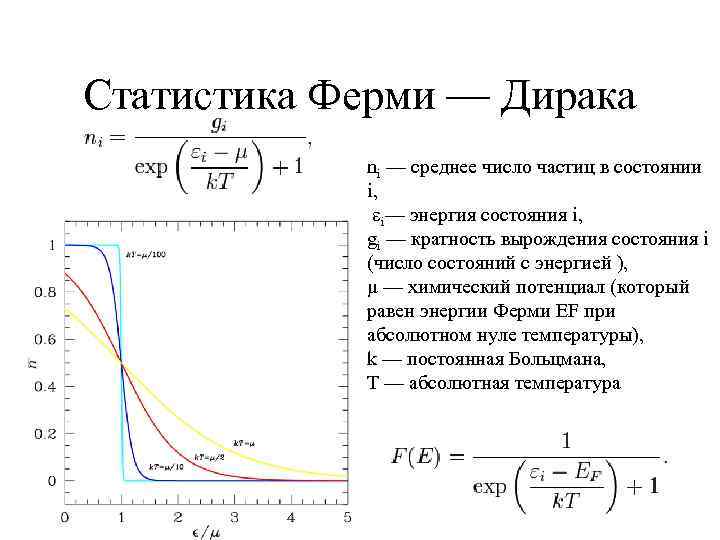Статистика Ферми — Дирака ni — среднее число частиц в состоянии i, i— энергия состояния i, gi — кратность вырождения состояния i (число состояний с энергией ), μ — химический потенциал (который равен энергии Ферми EF при абсолютном нуле температуры), k — постоянная Больцмана, T — абсолютная температура

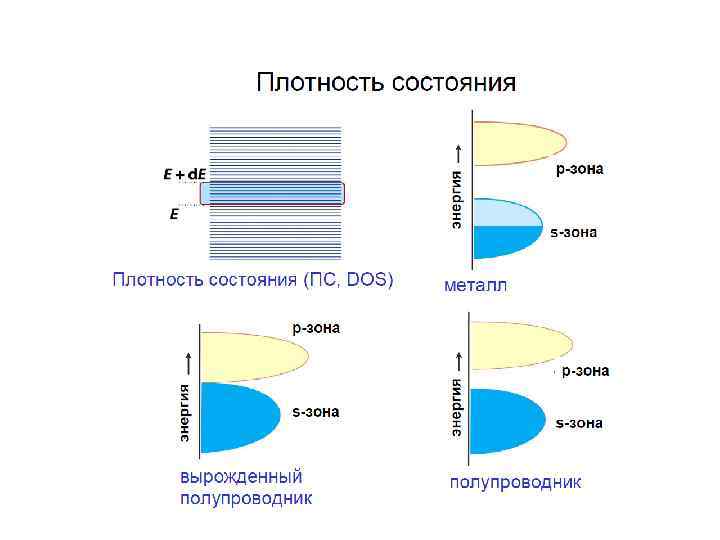
Плотность состояний Фазовое пространство частицы (в т. ч. электрона): координаты x, y, z + импульс px, py, pz Состояние частицы определяется точкой в фазовом пространстве Ячейка фазового пространства Ф= x y z px py pz Принцип неопределенности Гейзенберга: Для одномерного движения x p ħ => p h/ x Для трехмерного пространства p= px py pz=h 3/V 0 Элементарная ячейка пространства импульсов V 0 = x y z - только одно состояние микрочастицы (с учетом спина – 2 состояния электрона) Импульс p=h k => ограниченное число состояний в зоне Брюллиэна => для каждого значения энергии ограничено число частиц =>Плотность состояний Зависит от формы зоны Бриллюэна! g(E)=d. N/d. E Для свободного электрона:

Эффективная масса электрона в кристалле Свободный электрон в однородном электрическом поле E Сила: F=-e E Ускорение: a=F/m=-e E/m Электроны в кристалле движутся как волновой пакет. Групповая скорость =E/h Средняя скорость U=d /dk => зависит от дисперсионного закона E=f(k) Ускорение: Изменение энергии с учетом дает подставляя в выражение для ускорения получим Аналогия с законом Ньютона =>

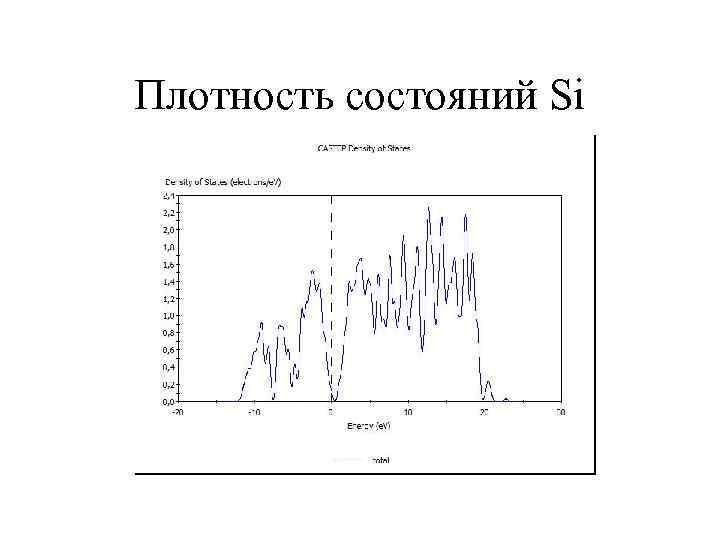Плотность состояний Si