Скачать презентацию ЭЛЕКТРОННАЯ ЦИФРОВАЯ ПОДПИСЬ ЭЦП Модель системы взаимно не
Презентация ЭЛЕКТРОННАЯ ЦИФРОВАЯ ПОДПИСЬ.ppt
- Количество слайдов: 81
ЭЛЕКТРОННАЯ ЦИФРОВАЯ ПОДПИСЬ (ЭЦП) Модель системы взаимно не доверяющими другу стороны
ЭЦП Требования к защищенному документообороту 1. Авторизованные документы должны храниться в открытом виде 2. Получатель должен иметь возможность убедиться, что именно указанный автор действительно является автором документа и иметь возможность это третьей стороне. 3. Невозможность (в том числе и получателю) выдать себя за автора документа
ЭЦП Требования к защищенному документообороту 4. Невозможность отказаться от авторства 5. Авторизация автоматически не может быть перенесена на другой документ 6. Позволять обнаружить факт внесения изменений в авторизованный документ
ЭЦП Традиционное решение (для бумажного документооборота) графическая подпись уникальная биометрическая характеристика субъекта, неразрывно связанная с документом посредством материального носителя <тексте документа><графическая подпись> ← материальный носитель(бумага) →
ЭЦП Требования: - текст документа зафиксирован в непреобразованном виде - подпись аутентична –ею можно убедить получателя или третью сторону, что именно указанный автор подписал документ, невозможно отказаться от авторства - подпись нельзя подделать, существует судебная графологическая экспертиза - подпись нельзя отделить от подписанного документа и перенести на другой документ - на материальном носителе остаются следы исправлений (неоговоренных)
ЭЦП Электронный документооборот функциональный аналог графической подписи – электронная цифровая подпись (ЭЦП) Определение (№ 63 -ФЗ "Об электронной подписи" 2011 г. ) Электронная подпись - информация в электронной форме, которая присоединена к другой информации в электронной форме (подписываемой информации) или иным образом связана с такой информацией и которая используется для определения лица, подписывающего информацию
ЭЦП Виды электронных подписей (№ 63 -ФЗ "Об электронной подписи" 2011 г. ) 1. Простая электронная подпись 2. Усиленная неквалифицированной электронная подпись) 3. Усиленная квалифицированная электронная подпись Простая электронная подпись, которая посредством использования кодов, паролей или иных средств подтверждает факт формирования электронной подписи определенным лицом
ЭЦП Простая электронная подпись, которая посредством использования кодов, паролей или иных средств подтверждает факт формирования электронной подписи определенным лицом
ЭЦП Усиленная (Неквалифицированной или Квалифицированная) электронная подпись, которая • 1) получена в результате криптографического преобразования информации с использованием ключа электронной подписи; • 2) позволяет определить лицо, подписавшее электронный документ; • 3) позволяет обнаружить факт внесения изменений в электронный документ после момента его подписания; • 4) создается с использованием средств электронной подписи.
ЭЦП Квалифицированная электронная подпись соответствует всем признакам неквалифицированной электронной подписи и следующим дополнительным признакам 1) ключ проверки электронной подписи указан в квалифицированном сертификате; 2) для создания и проверки электронной подписи используются средства электронной подписи, получившие подтверждение соответствия требованиям, установленным в соответствии с Федеральным законом.
ЭЦП Электронная подпись реквизит электронного документа, позволяющий установить отсутствие искажения информации в электронном документе с момента формирования ЭП и проверить принадлежность подписи владельцу (сертификата) ключа ЭП
ЭЦП Усиленная электронная подпись <тексте документа><усиленная ЭП> ← криптографическое преобразование →
ЭЦП Модель ЭЦП 1. Генерация ключевой пары (ключа подписи KR и ключа проверки подписи KU ) (субъект А) Ключ электронной подписи (закрытый личный) KRа– уникальный и предназначен для создания электронной подписи Ключ проверки электронной подписи (открытый) KUа - уникальный, однозначно связан с ключом электронной подписи и предназначенная для проверки подлинности электронной подписи
ЭЦП 2. Формирование подписи (субъект А) Для заданного электронного документа M с помощью своего закрытого ключа электронной подписи KRА субъект А вычисляет значение электронной подписи sign. A(M) Документ М, подписанный субъектом А Id A
ЭЦП 3. Проверка подписи (субъект В) Подписанный документ Id A
ЭЦП Требования к алгоритмам схемы ЭЦП Реализуемость 1. Вычислительно легко провести генерацию ключевой пары (Ключ электронной подписи KR, Ключ проверки электронной подписи KU) 2. Зная свой личный закрытый ключ подписи KRА, субъект А может вычислительно легко сформировать значение электронной подписи sign. A(M) 3. Любой субъект, зная открытый ключ проверки подписи KUА субъекта А и подписанный им документ
ЭЦП Криптостойкость 4. Вычислительно сложно (невозможно), зная открытый ключ проверки подписи субъекта А KUА и подписанный документ
ЭЦП • Возможность реализации ЭЦП с использованием однонаправленных функций с лазейкой • Fk(M) - однонаправленная функция с лазейкой (параметрическая функция)
ЭЦП • 1. Генерация ключевой пары • Ключ подписи (закрытый) KRА - параметр k • Ключ проверки подписи (открытый) KUА– функция Fk(M) • 2. Формирование подписи абонента A • Зная свой личный (закрытый) ключ подписи KRА = k, вычислительно легко получить • sign. A(M) = Fk-1(M) • 3. Проверка подписи • Зная открытый ключ проверки подписи KUА = Fk(M) вычислительно легко проверить действительность(подлинность) подписи субъекта А под документом М: • если Fk (sign. A(M)) = М, то подпись подлинная, в противном случае – ложная
ЭЦП Отличия ЭЦП от графической подписи 1. Не является биометрической характеристикой субъекта (факсимиле) 2. Значение ЭЦП одного субъекта под разными документами разное
ЭЦП Схема RSA 1. Генерация пары ключей (KU, KR) 1. 1 Выбрать простые р и q Вычислить n = p · q Вычислить Ф(n) = (p -1) * (q -1) 1. 2 Выбрать е, 1<е<Ф(n) и НОД (е, Ф(n)) =1 1. 3 Вычислить d из условия d = e-1 mod Φ(n) 1. 4 KU = {e, n} KR = {d}
ЭЦП Схема RSA 2. Формирование подписи (Id A) Открытый текст: М < n. A Вычисление подписи SA(M) = М d. A (mod n. A) Подписанный документ
ЭЦП Схема RSA 3. Проверка подписи Принятый документ
ЭЦП Схема RSA • Док-во: • Se (mod n) = (М d)e (mod n) = (М еd ) (mod n) = М (k Φ(n) +1) (mod n) = = ( М· (mod n) (М k Φ(n) ) (mod n)) (mod n = = (М· (М Φ(n) ) (mod n)) k(mod n)) = М Теорема Эйлера а Ф(n)Ξ 1 mod n НОД (а, n) =1
ЭЦП Схема RSA Пример 1. Генерация ключей 1. 1 Выбрать два простых числа: р = 7, q = 17. Вычислить n = p · q = 7 · 17 = 119. Вычислить Φ(n) = (p - 1) · (q - 1) = 96
ЭЦП Схема RSA 1. 2 Выбрать е е < 96 НОД (е, 96) =1 е = 5. 1. 3 Вычислить d из условия (d · e) = 1 mod 96 и d < 96 d = 77, так как 77 · 5 = 385 = 4 · 96 + 1 = 1 mod 96 1. 3 Закрытый ключ подписи KR = 77 Открытый ключ проверки подписи KU = {5, 119}
ЭЦП Схема RSA 2. Формирование подписи Сообщение М = 66 SA(M) = М d. A (mod n. A) = 6677 (mod 119) = 19 Подписанный документ
ЭЦП Схема RSA 3. Проверка подписи Принятый документ
ЭЦП Схема RSA Характеристики ЭП RSA 1. Схема с восстановлением 2. Детерминированная 3. Криптостойкость ≤ сложность задачи факторизации = субэкспоненциальная сложность 4. Длина ЭП = размер модуля ЭП 5. Сложность реализации = f(размер модуля ЭП)
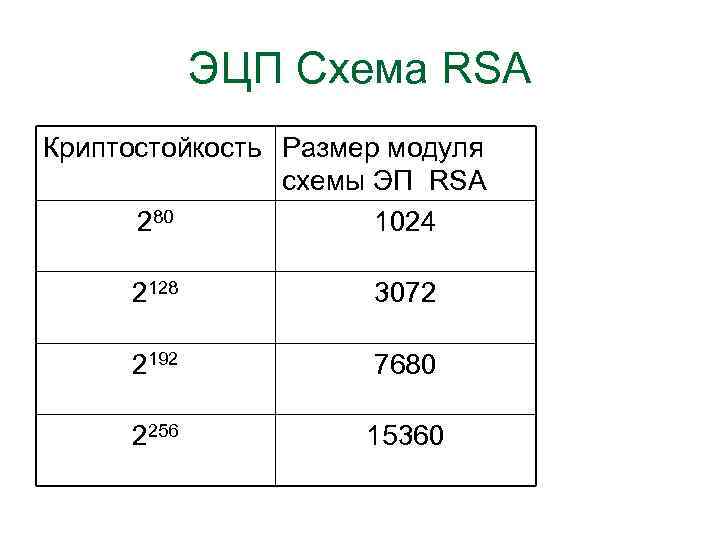ЭЦП Схема RSA Криптостойкость Размер модуля схемы ЭП RSA 280 1024 2128 3072 2192 7680 2256 15360
ЭЦП Функция хэширования в протоколе ЭП 1. Увеличение скорости 2. Повышение безопасности SA(M 1) = М 1 d. A (mod n. A) SA(M 2) = М 2 d. A (mod n. A) SA(M 1) * SA(M 2) =(М 1*М 2) d. A (mod n. A) = = SA(M 1*М 2) (mod n. A)
ЭЦП Криптостойкость протокола ЭП = = min {криптостойкость схемы ЭП, криптостойкость функции хэширования}
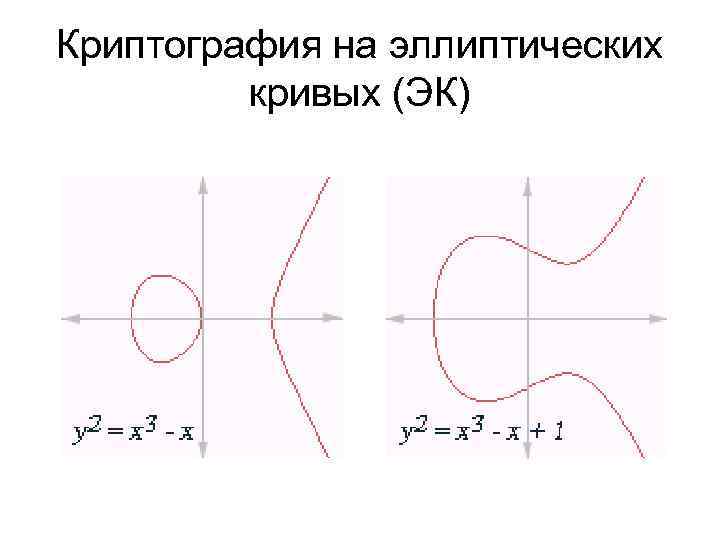
Криптография на эллиптических кривых (ЭК) Эллиптическая кривая E над полем действительных чисел R ( в форме Вейерштрасса) E: y 2 = x 3 + ax + b, a, b € R ЭК не имеет особых точек, если ∆ = -16(4 а 3+27 b 2) ≠ 0
Криптография на эллиптических кривых (ЭК)
Криптография на эллиптических кривых (ЭК) • Свойства ЭК: - симметрична относительно оси y - (-R) € E - (- R) – отрицание точки R - R =(x, y) -R = (x, -y) - является гладкой, то есть в каждой точке можно провести касательную - график имеет две части, если ∆>0 , и одну — если ∆<0 - прямая, проходящая через две различные точки P, Q € E, имеет только одну дополнительную точка пересечения
Криптография на эллиптических кривых (ЭК) Сложение точек ЭК (групповая операция) P + Q + (-R) = 0 R = P + Q Несобственная точка 0 - единичный элемент группы точек ЭК Р + (-Р) = 0 Р + 0 = Р Удвоение точки Р + Р = 2*Р =R
Криптография на эллиптических кривых (ЭК) Геометрическая интерпретация
Криптография на эллиптических кривых (ЭК)
Криптография на эллиптических кривых (ЭК)
Криптография на эллиптических кривых (ЭК)
Криптография на эллиптических кривых (ЭК)
Криптография на эллиптических кривых (ЭК) Алгебраическая интерпретация
Криптография на эллиптических кривых (ЭК) P = {Xp, Yp} Q = {Xq, Yq} R = P + Q = {Xr, Yr} 1) Xp ≠ Xq S = (Yp − Yq)/(Xp − Xq) Xr = S 2 - Xp − Xq Yr = − Yp + S * (Xp − Xr) S - угловой коэффициент секущей, проведенной через точки P и Q.
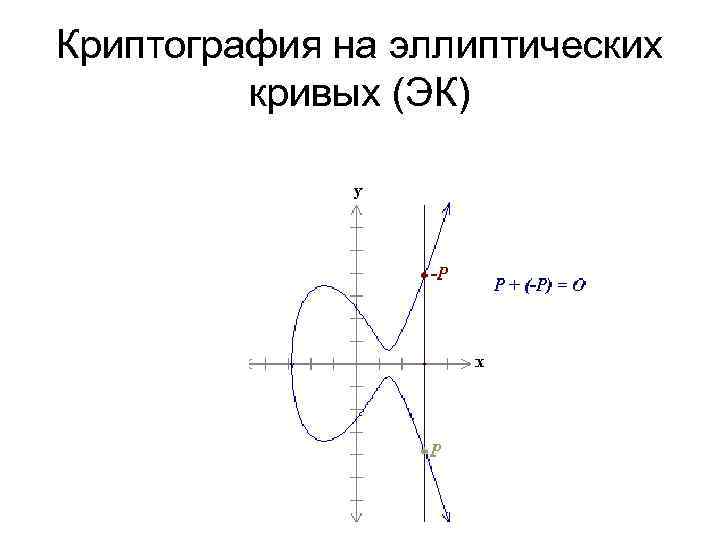
Криптография на эллиптических кривых (ЭК) 2) Xp = Xq S = (3*Xp 2 + a) / (2*Yp) Xr = S 2 – 2*Xp Yr = S * (Xp − Xr) − Yp
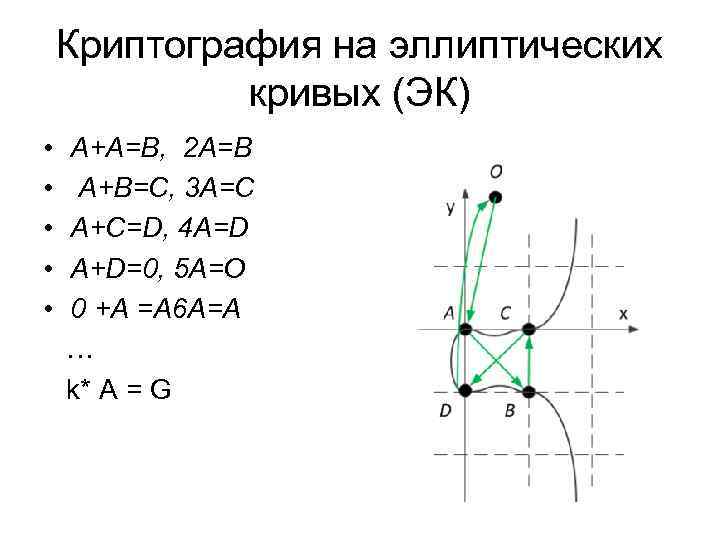Криптография на эллиптических кривых (ЭК) • A+A=B, 2 A=B • A+B=C, 3 A=C • A+C=D, 4 A=D • A+D=0, 5 A=O • 0 +A =A 6 A=A … k* A = G
Криптография на эллиптических кривых (ЭК) Эллиптическая кривая E над конечным полем Fp Ep: y 2 = x 3 + ax + b, a, b € Fp р – простое число ЭК не имеет особых точек, если ∆ = -16(4 а 3+27 b 2) ≠ 0 mod p
Эллиптическая кривая Ep над конечным полем • Пример • Построить • Ер: y 2 =х3+х над F 23 1. х=1 2. z= х3+х mod 23 = (1+1) mod 23 = 2 3. Если z = 0, то существует только одна точка (х, 0) с заданной х-координатой
Эллиптическая кривая Ep над конечным полем • Так как z ≠ 0, проверяем существование такого y, чтобы z = y 2 mod p • Критерий Эйлера (z – квадратичный вычет) Z (p-1)/2 =1 modp 2 (23 -1)/2 mod 23 = 211 mod 23 = = 2048 mod 23 = (89*23+1) mod 23 =1
Криптография на эллиптических кривых (ЭК) 4. Т. к. критерий Эйлера выполняется, то уравнению ЭК Ер удовлетворяют 2 точки (х, y 1) и (х, y 2) 5. Если р Ξ 3 mod 4, то y 1=+z (p+1)/4 mod p = 2 (23+1)/4 mod 23 = 26 mod 23 = 64 mod 23 = 18 y 2= -z (p+1)/4 mod p = p - z (p+1)/4 mod p = = 23 – 18 = 5
Эллиптическая кривая Ep над конечным полем 6. Т. о. (1, 5); (1, 18) є Е 23 y 2 = х3 +х
Эллиптическая кривая Ep над конечным полем # Ер - порядок эллиптической кривой Ер Число всех ее точек (х, у) є Ер (вместе с несобственной точкой О) Теорема Haase P+1 -2*√p ≤ # Ер ≤ P+1+2*√p E 23 23+1 -2 *√ 23≤ # Е 23 ≤ 23+1+2 *√ 23 14. 4≤ # Е 23 ≤ 33. 6
Эллиптическая кривая Ep над конечным полем • Ер =х3+х над. F 23 (0, 0), (1, 5), (1, 18), (9, 5), (9, 18), (11, 10), (11, 13) (13, 5), (13, 18), (15, 3), (15, 20), (16, 8), (16, 15), (17, 10), (17, 13), (18, 10), (18, 13), (19, 1), (19, 22), (20, 4), (20, 19), (21, 6), (21, 17) # Ер = 23
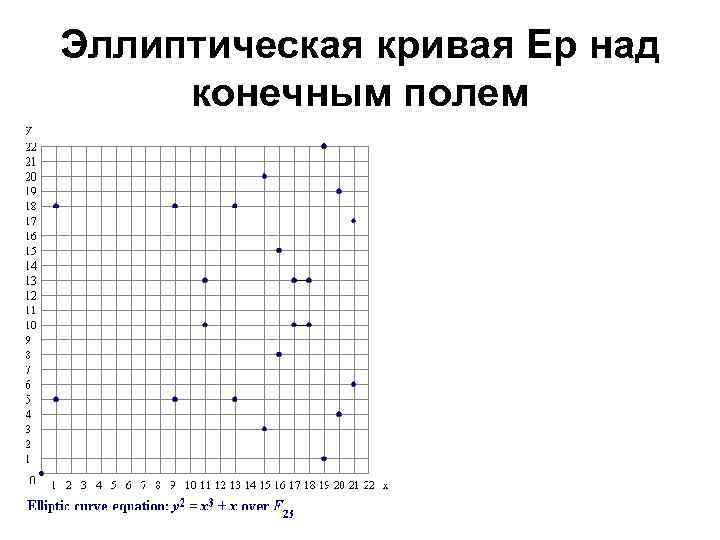Эллиптическая кривая Ep над конечным полем
Криптография на эллиптических кривых (ЭК) P = {Xp, Yp} Q = {Xq, Yq} R = P + Q = {Xr, Yr} 1) Xp ≠ Xq S = (Yp − Yq)/(Xp − Xq) (mod p) Xr = S 2 - Xp − Xq (mod p) Yr = − Yp + S * (Xp − Xr) (mod p) S - угловой коэффициент секущей, проведенной через точки P и Q.
Криптография на эллиптических кривых (ЭК) 2) Xp = Xq S = (3*Xp 2 + a) / (2*Yp) (mod p) Xr = S 2 – 2*Xp (mod p) Yr = S * (Xp − Xr) − Yp (mod p)
Криптография на эллиптических кривых (ЭК) • • • Группа точек эллиптической кривой Е 7: y 2 = x 3+x+3 mod 7 {(4, 1) (4, 6) (5, 0) (6, 1) (6, 6) 0} # Е 7 = 6
• Группа образующей точки Р є Ep • Множество точек q*Р є Ep • Порядок точки Р є Ep • наименьшее натуральное число m≠ 0, для которого m*Р= О
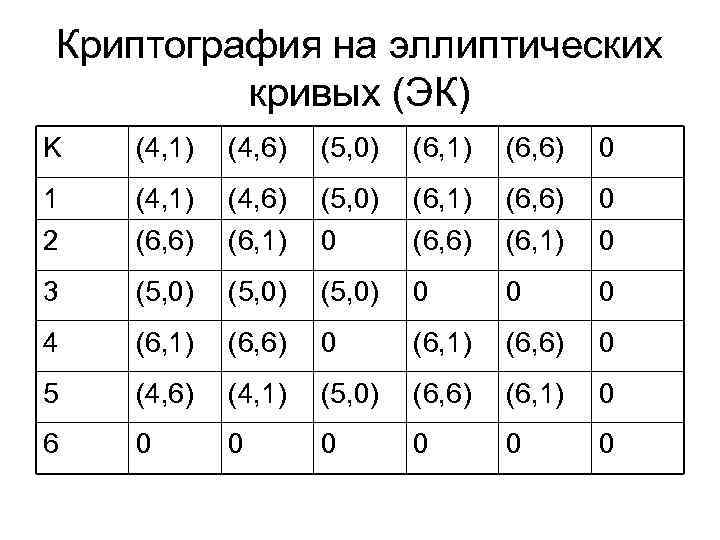Криптография на эллиптических кривых (ЭК) K (4, 1) (4, 6) (5, 0) (6, 1) (6, 6) 0 1 2 (4, 1) (6, 6) (4, 6) (6, 1) (5, 0) 0 (6, 1) (6, 6) (6, 1) 0 0 3 (5, 0) 0 0 0 4 (6, 1) (6, 6) 0 5 (4, 6) (4, 1) (5, 0) (6, 6) (6, 1) 0 6 0 0 0
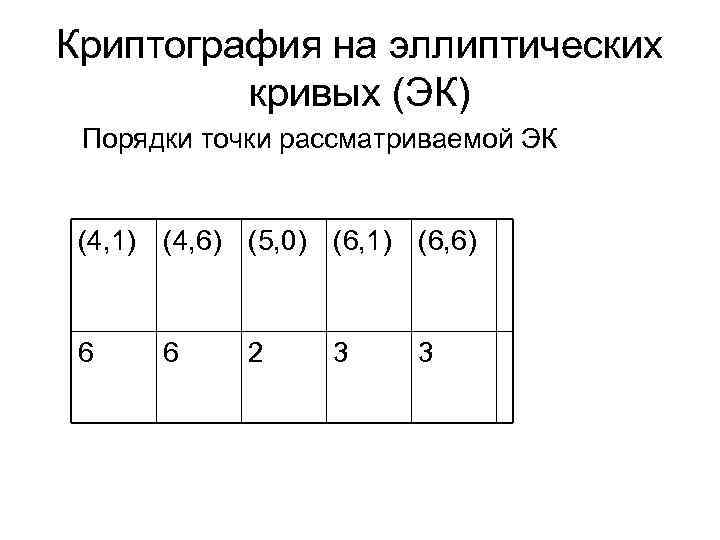Криптография на эллиптических кривых (ЭК) Порядки точки рассматриваемой ЭК (4, 1) (4, 6) (5, 0) (6, 1) (6, 6) 6 6 2 3 3
Эллиптическая кривая Ep над конечным полем Дискретное логарифмирование Для заданной ЭК Ер, образующей точки Q и ее образа Р найти такое целое k, что Р= k*Q Экспоненциально сложная задача сложность порядка О(√r), где r = # Ер - порядок группы точек эллиптической кривой
Протокол ЭЦП на ЭК Параметры схемы цифровой подписи (общие для всех абонентов ) 1. ЭК Ep (a, b) , а, b € Fp ∆ = -16(4 а 3+27 b 2) ≠ 0 где р – модуль эллиптической кривой – большое простое число Fp - конечное простое поле # Е = m
Протокол ЭЦП на ЭК 2. точка Р (≠ 0) є Ep (a, b) – базовая точка q – порядок точки Р - большое простое число ( q*Р =О) Дополнительные условия: 1. m ≠ p 2. р > 2255 3. pt ≠ 1 mod q, t = 1, 2, . . . В, В ≥ 31 4. 2*2254 < q < 2256 5. m = h* q (h = 1, 2, 3, …)
Протокол ЭЦП на ЭК ГОСТ Р 34. 10 -2001 • Генерация ключей • Каждый пользователь схемы: • - личный закрытый ключ подписи KU– случайное целое число d , 0 < d < q ; • - несекретным открытый ключ проверки подписи KR • KR = Q Q = d*P (d – образ точки P) (xq – x- координата точки Q)
Протокол ЭЦП на ЭК Формирование цифровой подписи 1. Вычисляет хэш-образ подписываемого сообщения М HM = h(М) 2. Представить HM в виде целого число e = HM (mod q) Если е = 0, то определить е = 1
Протокол ЭЦП на ЭК 3. Сгенерировать случайное целое число k 0 < k < q. 4. Вычислить точку C = k*P и определить r = xс (mod q) где xс -координата точки С. Если r = 0, то вернуться к шагу 3. 5. Вычислить S = (r*d + k* e) (mod q) Если s = 0, то вернуться к шагу 3.
Протокол ЭЦП на ЭК 6. Определить цифровую подпись
Протокол ЭЦП на ЭК Проверка цифровой подписи 1. Вычислить HM = h(М) 2. Представить HM как целое число e = HM (mod q) Если е = 0, то определить е = 1
Протокол ЭЦП на ЭК 3. Вычислить V = e-1(mod q) 4. Вычислить Z 1 = S*V (mod q) Z 2 = - r*V (mod q)
Протокол ЭЦП на ЭК 5. Вычислить точку ЭК С' = Z 1*P + Z 2*Q R = xc’ (mod q) где xc’ – х-координата точки С’. 7. Если R = r , то подпись истинная (принимается), в противном случае, подпись ложная (не принимается)
Протокол ЭЦП на ЭК Док-во: Из уравнения для S k = e -1 *(s - r*d ) (mod q) = (e -1 *s – e -1 *r*d) (mod q)= (v*s – v*r*d) (mod q)=(Z 1+Z 2*d) (mod q) С другой стороны C’ = Z 1*P + Z 2* Q = Z 1* P +Z 2* d* P = (Z 1+Z 2*d)* P = = k* P = C Следовательно, R=r
• Пример вычисления ЦП на эллиптической кривой
• Выбранная ЭК должна обеспечивать высокую скорость вычислений (особенно умножение точки на целое число). Это достигается выбором соответствующих характеристик поля и вида ЭК (например, допускающих эффективное применение комплексного умножения или иной способ быстрого умножения точки на целое число). • Задача выбора вида ЭК и базовой точки ЭК является сложной задачей. В ГОСТ Р 34. 102001 процесс выбора не рассмотрен. Есть рекомендации NIST, Certicom по выбору ЭК.
Методы реализации и характеристики криптопреобразований на ЭК зависят от 1. Вида конечного поля Fp 2. Вида ЭК (случайная кривая, кривая Коблица) 3. Представления координат точек ЭК (аффинное или проективное)
Случайный выбор ЭК 1. Выбрать большое конечное поле Fp 2. Выбрать случайным образом {x 0, y 0, a} є Fp 3. Вычислить b = y 0 – (x 0+ a*x 0) 4. Проверит выполнение требований к ЭК
• Проективные координаты •
• Безопасность схемы ЭЦП на ЭК 1. Сложность задачи вычисления дискретного логарифма на ЭК 2. Сложность задачи предсказания случайного числа 3. Сложность нахождения коллизии функции хэширования
• Атака на генератор случайных чисел
Сравнение ЭЦП RSA и ГОСТ Р 34. 10 -2001 (ECDSA) ЭЦП RSA ЭЦП ГОСТ Р 34. 10 -2001, ECDSA Схема с Использует специальные восстановлением проверочные соотношения Детерминированная Вероятностная Субэкспоненциально Экспоненциально сложная задача факторизации вычисления дискретного логарифма на ЭК Sign – одно число Пара чисел (r, s)
Сравнение ЭЦП RSA и ГОСТ Р 34. 10 -2001 (ECDSA) • Сложность реализации Крипто. RSA ГОСТ RSA : стойкость Р 34. 10 -2001 ГОСТ Р 34. 102001 80 1024 160 6 : 1 128 3072 256 12 : 1 192 7680 384 20 : 1 256 15360 512 30 : 1
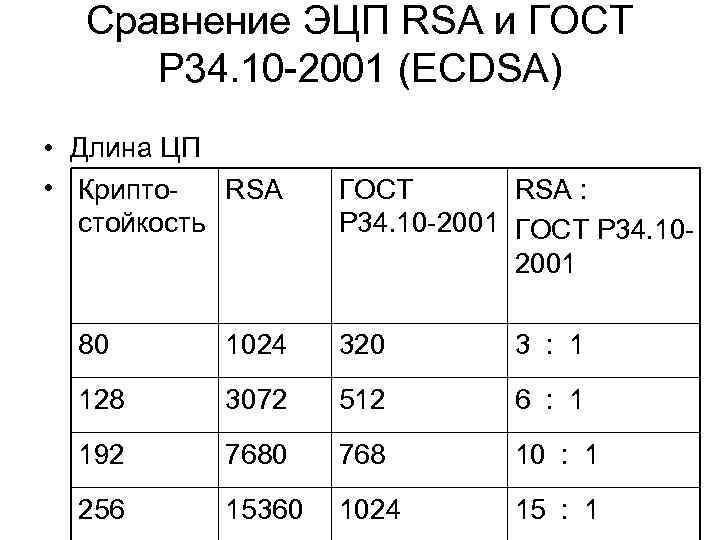Сравнение ЭЦП RSA и ГОСТ Р 34. 10 -2001 (ECDSA) • Длина ЦП • Крипто. RSA стойкость ГОСТ RSA : Р 34. 10 -2001 ГОСТ Р 34. 102001 80 1024 320 3 : 1 128 3072 512 6 : 1 192 7680 768 10 : 1 256 15360 1024 15 : 1
ГОСТ Р 34. 10 -2012 • 1. Функция хеширования ГОСТ Р 34. 112012 • 2. Размер хэш- образа • 3. Параметры ЭК