Электромагнитная индукция Майкл Фарадей Майкл 1791 -1867

Электромагнитная индукция Майкл Фарадей Майкл (1791 -1867) – великий английский учёный, творец общего учения об электромагнитных явлениях, в котором все явления рассматриваются с единой точки зрения. Фарадей впервые ввёл представления об электрическом и магнитном полях. “Там, где математики видели центры напряжения сил дальнодействия, Фарадей видел промежуточный агент. Где они не видели ничего, кроме расстояния, удовлетворяясь тем, что находили закон распределения сил, действующих на электрические флюиды(т. е. Заряды с современной точки зрения), Фарадей искал сущность реальных явлений, протекающих в среде” (Д. Максвелл).

1. Вводные замечания 1) Поток вектора индукции Ф=BScos 2) 2) Магнитное взаимодействие – чисто релятивистский эффект 3) Магнитное поле – удобное представление магнитного взаимодействия 4) Сила Лоренца

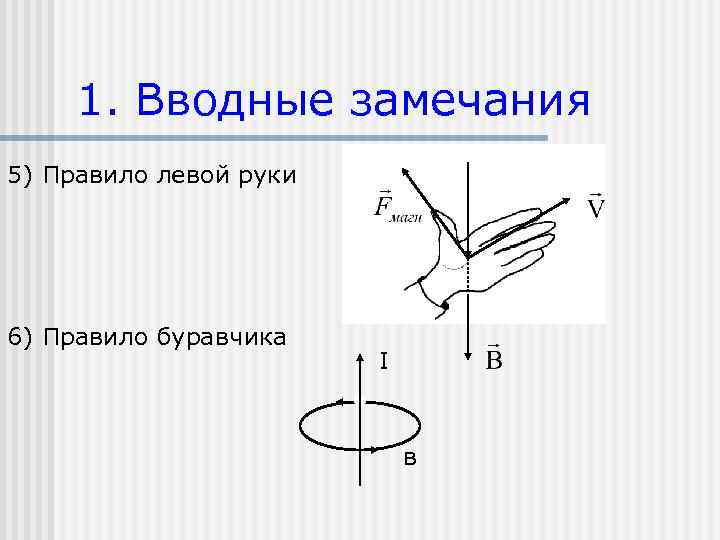1. Вводные замечания 5) Правило левой руки 6) Правило буравчика I в

Электромагнитная индукция (ЭМИ) 1) Открытие ЭМИ – Фарадей (1831 г. ) 2) -Идея (1821) 3) При постоянном В не возникает. 4) -Швейцарец Колладон – просмотрел! 5) -Фарадей обнаружил ток индукции при включении 6) и выключении тока во втором контуре. Раз I создаёт В, то и В создаёт I

Электромагнитная индукция (ЭМИ) -Опыты Фарадея ЭДС в контуре можно создавать тремя способами: 1. Двигая контур в магнитном поле. 2. 2. Двигая магнит вблизи провода. 3. 3. Меняя ток в соседнем проводе. 4. 3. Т. II; 242 ; Купер I, 318

Электромагнитная индукция (ЭМИ) 2) Закон Фарадея (1831) Обнаружить явления можно с единых позиций, описать через изменение потока Ф. (1) Закон Фарадея. Не важно, как менять Ф, всегда получим индукционный ток, определяемый , согласно (1)

Электромагнитная индукция (ЭМИ) По Фарадею Явление ЭМИ состоит в том, что во всяком замкнутом контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток

Электромагнитная индукция (ЭМИ) 3) Правило Ленца (1833) Индукционный ток всегда направлен так, чтобы препятствовать причине, его вызывающей. S N 3. Т. II, 243

Электромагнитная индукция (ЭМИ) 3) Физика ЭМИ, вывод закона Фарадея I. II. Проводник(контур) движется в магнитном поле. a) Соотв. B=const (однородное поле. ) т. е.

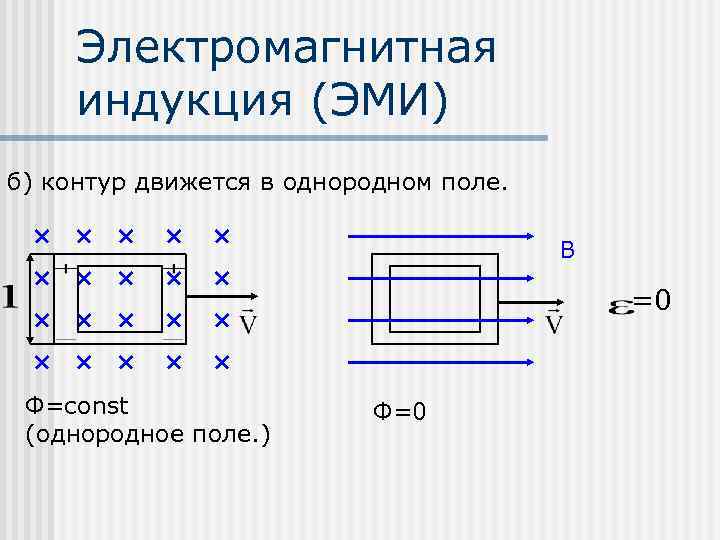Электромагнитная индукция (ЭМИ) б) контур движется в однородном поле. В =0 Ф=const (однородное поле. ) Ф=0

Электромагнитная индукция (ЭМИ) в) контур движется в неоднородном магнитном поле.

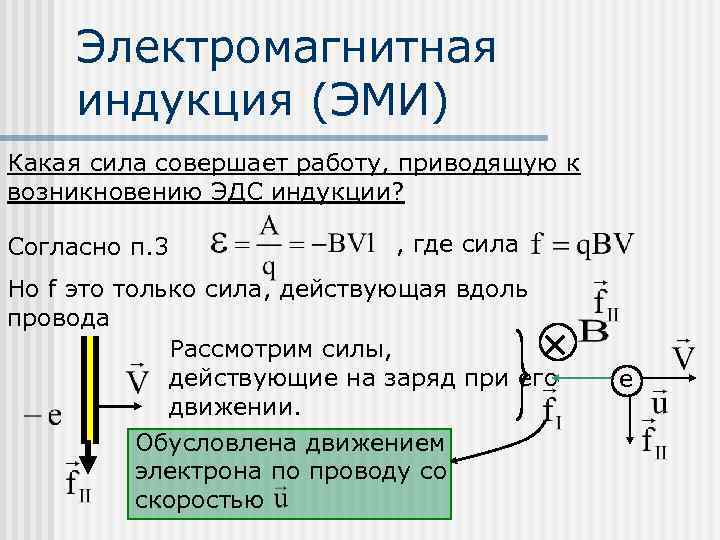Электромагнитная индукция (ЭМИ) Какая сила совершает работу, приводящую к возникновению ЭДС индукции? Согласно п. 3 , где сила Но f это только сила, действующая вдоль провода Рассмотрим силы, действующие на заряд при его движении. Обусловлена движением электрона по проводу со скоростью е

Электромагнитная индукция (ЭМИ) Чтобы двигать провод со скоростью V нужно всё время прилагать Чтобы уравновесить силу нужно приложить Т. е. должно За счёт этой механической силы и совершается работа

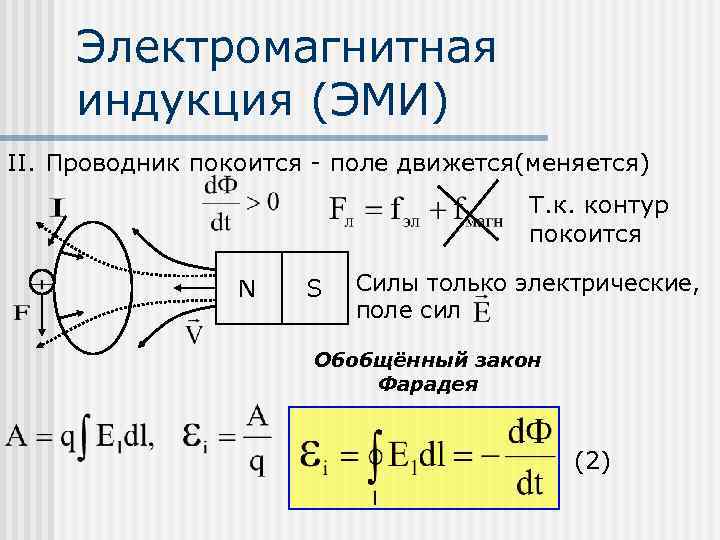Электромагнитная индукция (ЭМИ) II. Проводник покоится - поле движется(меняется) Т. к. контур покоится N S Силы только электрические, поле сил Обобщённый закон Фарадея (2)

Электромагнитная индукция (ЭМИ) По Максвеллу: Переменные магнитные поля возбуждают вихревые электрические поля

Электромагнитная индукция (ЭМИ) Поле вихревое – непотенциальное! С § 69, c 192 | я. п. I, 436 З. Т. 243

Обобщение Опыты Фарадея 1) Провод движ. в 2) движ. отн пров. 3) измен во врем. Правило Ленца М а к с в е л л ЭДС Сила Лоренца З-н Фарадея Обобщение на неподв. пров. и меняющееся В Переменное вызывает переменное -вихревое

Самоиндукция

Введение Закон Био. Савара-Лапласа: Прямой ток Центр кругового тока На оси кругового тока

Введение Бесконечно длинный соленоид Во всех случаях H=геометр. const I Т. е. магнетик) Видим! , если (не ферро-

Единицы измерения L За единицу индуктивности в СИ принимают индуктивность такого проводника, у которого при I=1 A возникает сцепленный с ним полный поток Ф=1 Вб. Это Генри (Гн) В гауссовой. системе(см), когда при I=1 сгсм(10 А) возникает Ф=1 Мкс= Вб. (сантиметр)

Самоиндукция (с-и) Самоиндукция – явление, когда ЭДС индукции возникает в том же контуре, в котором изменяют ток. - Статическое определение L L – коэффициент самоиндукции - Динамическое определение L

Пример: Индуктивность соленоида , где N=nl , где H=n. I Тогда:

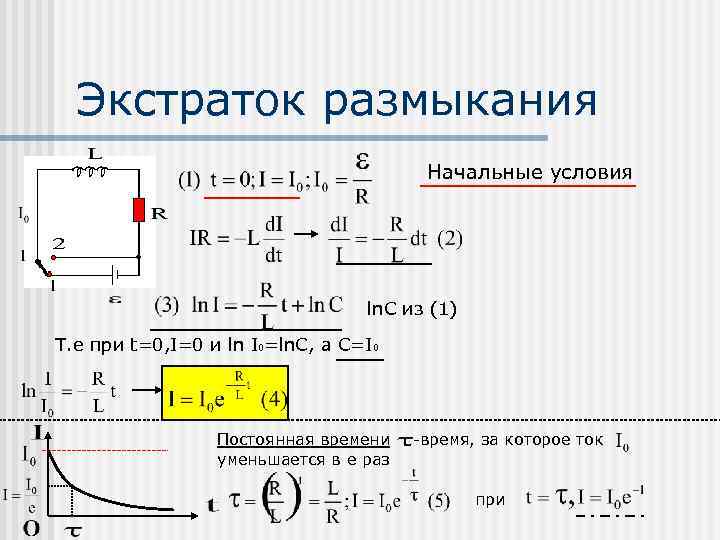Экстраток размыкания Начальные условия ln. C из (1) Т. е при t=0, I=0 и ln I 0=ln. C, а С=I 0 Постоянная времени уменьшается в e раз -время, за которое ток при

Перенапряжения при резком выключении И согл. (4) При резком размыкании, когда Пробой Дуга Обгорание рэле Гибель переключателя Пример: L=0. 1 Г R=0. 7(Ом) Когда I 0 упадёт в 2 раза? И при Контур с L нельзя резко размыкать!

Замыкание цепи Начальные условия при t=0, I=0 Из нач. условия (1) Ток из-за нарастает медленнее (1)

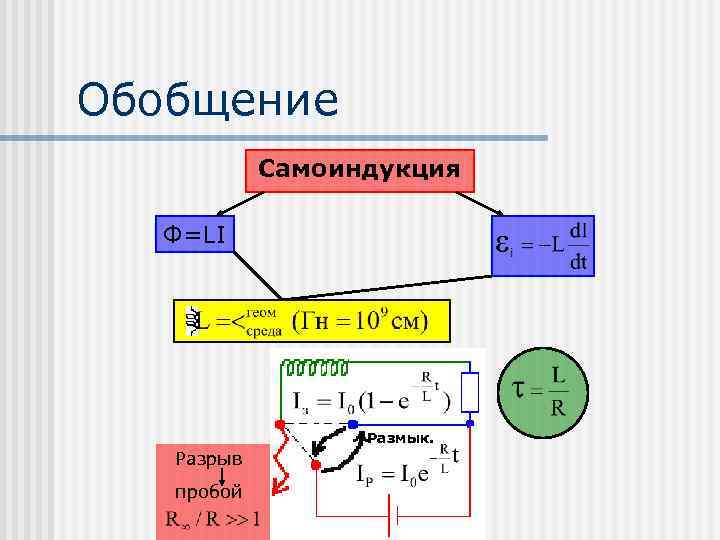Обобщение Самоиндукция Ф=LI Размык. Разрыв пробой

Взаимная индукция

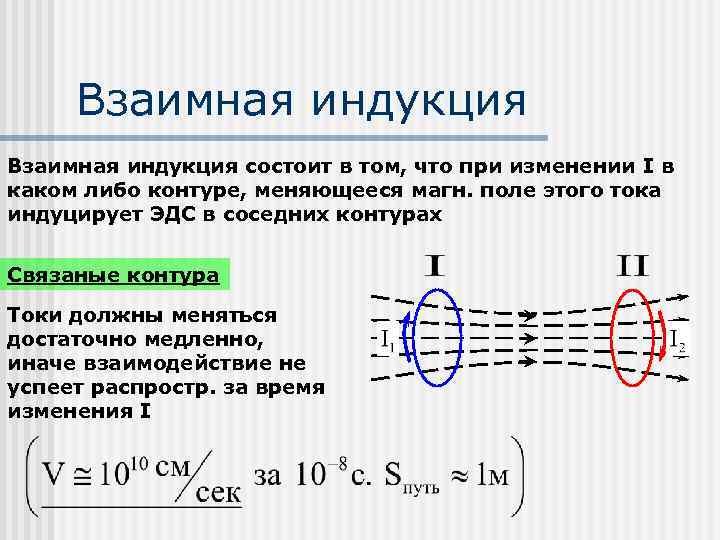Взаимная индукция состоит в том, что при изменении I в каком либо контуре, меняющееся магн. поле этого тока индуцирует ЭДС в соседних контурах Связаные контура Токи должны меняться достаточно медленно, иначе взаимодействие не успеет распростр. за время изменения I

Взаимная индукция Статическое определение Коэф. Взаимной индукции равен потоку магнитной индукции, созданному единичным током в одном из контуров и пронизывающему второй контур Динамическое определение двух контуров равен ЭДС индукции, возникающей в одном из контуров при изменении I в другом на единицк силы тока за единицу времени Изменяется ток: I 1 I 2

Взаимная индукция Теорема взаимности. Это надо доказать ! Единица измерения взаимной индукции – Генри (Гн) Величина коэффициента взаимной индукции определяется только геометрической формой, размерами контуров и их относительным расположением За исключением ферромагнитных тел, для которых (H)

Взаимная индукция Энергия магнитного поля Один контур При увеличении тока возникает , препятствующая его росту, при уменьшении – наоборот. Для преодоления необходимо совершить работу , когда выключаем цепь, эта энергия высвобождается. Совершая работу мы увеличиваем ток, и, следовательно, , т. е. запасаем магнитную энергию. Работа против магнитного поля идёт на образование энергии

Взаимная индукция Если в данный момент I=I , то мощность ЭДС индукции Согласно (1) и (2): Ток меняем от I до 0 Энергия магнитного поля тока

Взаимная индукция Плотность энергии магнитного поля Выразим W через B или H. Рассмотрим однородное поле. Это поле создаётся соленоидом. Ранее мы установили: Если поле неоднородно:

Взаимная индукция Обобщение на случай N контуров, док-во теоремы взаимности, т. е. что L 21=L 12 Рассмотрим 2 контура Включаем Iй (В самом Iм контуре) Затем включаем IIй И ещё работа против ЭДС взаимной индукции Тогда полная энергия Теперь поменяем порядок включения контуров, тогда: Т. к. энергия системы токов не должна зависеть от последовательности их образования, то Для энергии N контуров

Уравнения Максвелла

Максвелл, Джеймс Клерк Д. К. Максвелл (1831 -1879) - великий английский учёный, создатель теории электромагнетизма. В 1860— 1865 Максвелл создал теорию электромагнитного поля, которую сформулировал в виде системы уравнений (уравнения Максвелла). Уравнения Максвелла составляют основу как электротехники и радиотехники, так и теории любых электромагнитных явлений в любых средах. В 1861 г. он обнаружил, что свет — это разновидность электромагнитных волн. Максвелл также создал Создал кинетическую теорию газов (1859 г. ) и вывел соотношение для распределения цастиц газов по скоростям, получившего название распределения Максвелла.

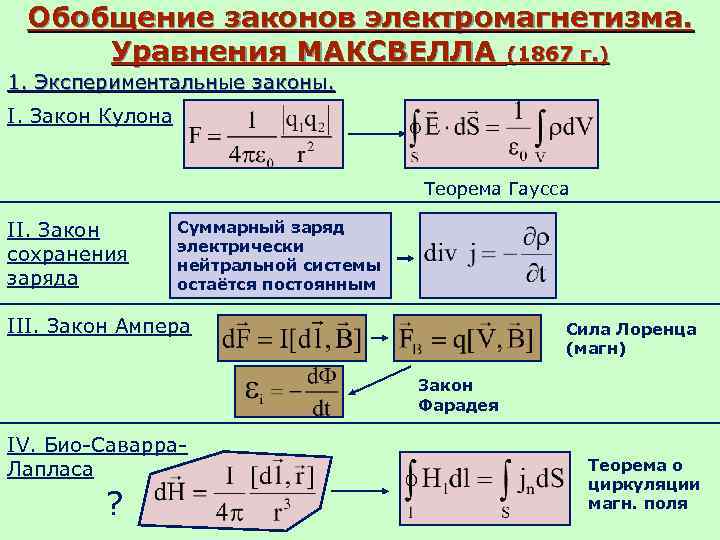Обобщение законов электромагнетизма. Уравнения МАКСВЕЛЛА (1867 г. ) 1. Экспериментальные законы. I. Закон Кулона Теорема Гаусса II. Закон сохранения заряда Суммарный заряд электрически нейтральной системы остаётся постоянным III. Закон Ампера Сила Лоренца (магн) Закон Фарадея IV. Био-Саварра. Лапласа ? Теорема о циркуляции магн. поля

Обобщённый закон Фарадея Свойства вихревого поля Ев 1. Это поле не является кулоновским – оно вызвано не каким-то распределением зарядов, а движением источника магнитного поля. 2. Силовые линии Ев замкнуты – поэтому оно называется вихревым. 3. Ев не является полем потенциальным 4. Энергетической характеристикой этого поля является не потенциал, а электродвижущая сила индукции. 5. Согласно Максвелла проводник служит только тем объектом, в котором электрические силы себя проявляют. 6. Электрическое поле может быть как потенциальным Еg, так и вихревым + Е в. - Для потенц. поля то справедливо общее выражение

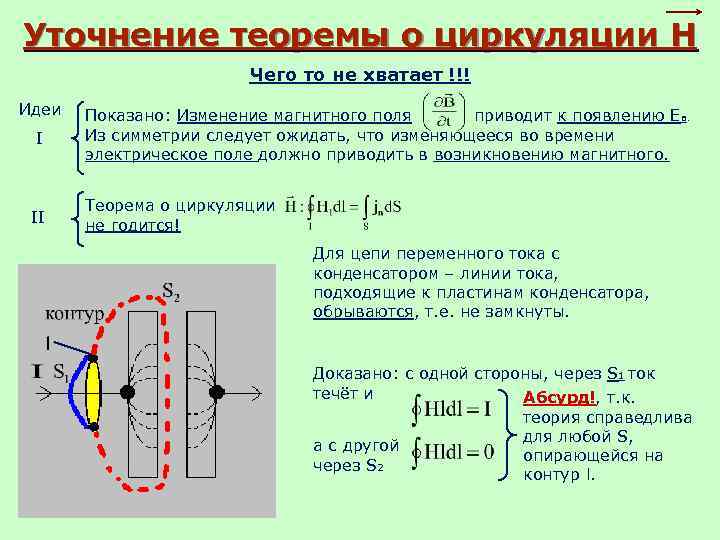Уточнение теоремы о циркуляции Н Чего то не хватает !!! Идеи I II Показано: Изменение магнитного поля приводит к появлению Ев. Из симметрии следует ожидать, что изменяющееся во времени электрическое поле должно приводить в возникновению магнитного. Теорема о циркуляции не годится! Для цепи переменного тока с конденсатором – линии тока, подходящие к пластинам конденсатора, обрываются, т. е. не замкнуты. Доказано: с одной стороны, через S 1 ток течёт и Абсурд!, т. к. теория справедлива для любой S, а с другой опирающейся на через S 2 контур l.

Ток смещения Чтобы замкнуть ток и устранить противоречие Максвелл формально ввёл так называемый ток смещения При этом полагая, что Ток проводимости тогда Вычисление : Максвелл предположил, что линии на поверхности обкладок в непрерывно переходят Плотность тока внутри пластины Между пластинами есть переменное поле На границе обкладок Линии тока смещения создают непрерывные линии тока. и одинаково направлены з а р я д к а

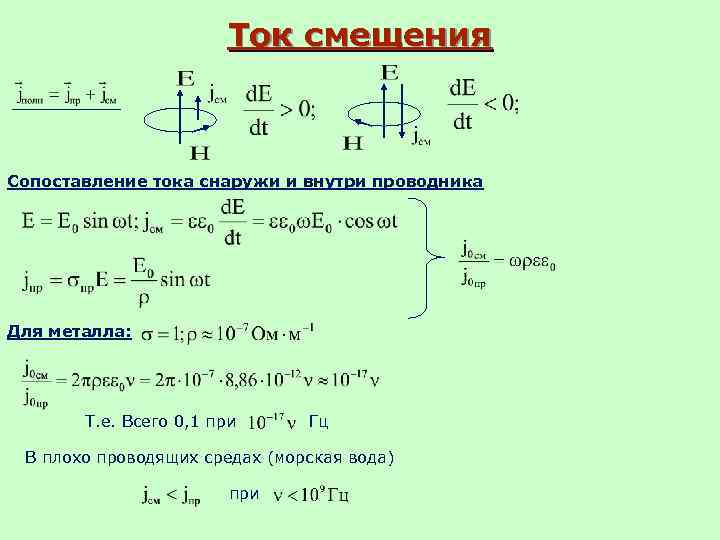Ток смещения Сопоставление тока снаружи и внутри проводника Для металла: Т. е. Всего 0, 1 при Гц В плохо проводящих средах (морская вода) при

Ток смещения Из всех свойств, присущих току присуще лишь одно – создавать в окружающем пространстве магнитное поле Уточнённая теорема о циркуляции Таким образом Изменяющееся во времени электрическое поле создаёт вихревое магнитное

Приложение к ур-ниям Максвелла в дифференциальной форме Теоремы Стокса и Остроградского-Гаусса Т. Стокса Т. Остроградского Гаусса где

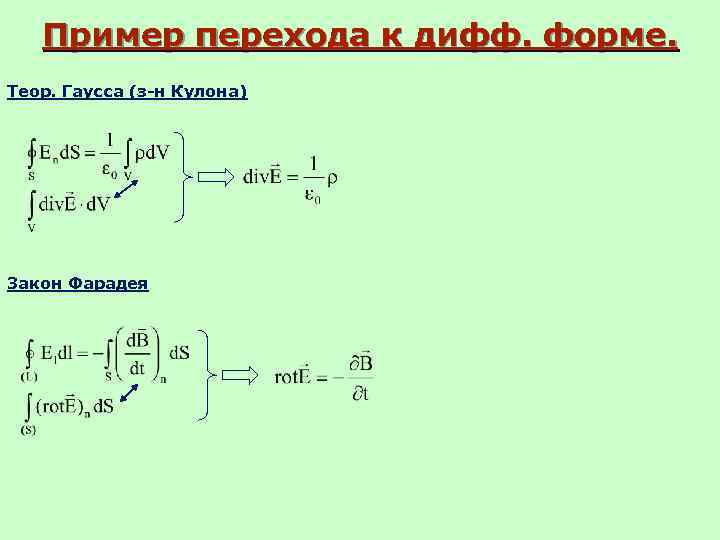Пример перехода к дифф. форме. Теор. Гаусса (з-н Кулона) Закон Фарадея

Уравнения Максвелла (собираем) I II Интегральная форма Дифференциальная форма Материальные уравнения

Свойства уравнений Максвелла 1. Источниками электрического поля могут быть электрические заряды или меняющиеся во времени магнитные поля. Магнитные поля могут возбуждаться либо движущимися электрическими зарядами(токами), либо переменными электрическими полями 2. В природе обнаружены электрические заряды и НЕ ОБНАРУЖЕНЫ заряды магнитные. Дирак если бы обнаружился МОНОПОЛЬ, то к источникам магнитного поля добавились бы магнитные заряды, а к источникам электрического поля магнитные токи. Уравнения Максвелла справедливы для областей, где нет магнитных зарядов и магнитных токов. 3. и независимы, когда источник проводимости. 4. Из уравнений Максвелла следует возможность существования ЭМ волн. 5. Уравнения Максвелла инвариантны относительно преобразований Лоренца - только заряды, а - только токи

Закон сохранения заряда уравнение непрерывности Суммарный заряд электрически нейтральной системы остаётся ПОСТОЯННЫМ -Уравнение непрерывности (в интегральной форме) Для постоянного тока Q=const и

Вихревые токи

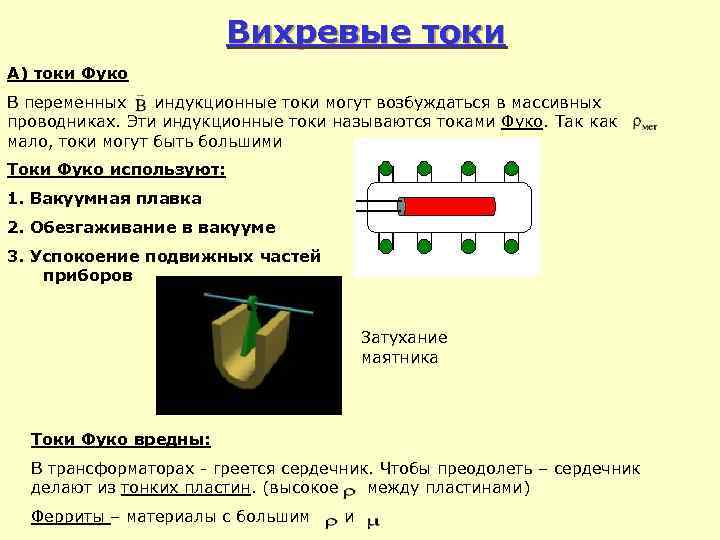Вихревые токи А) токи Фуко В переменных индукционные токи могут возбуждаться в массивных проводниках. Эти индукционные токи называются токами Фуко. Так как мало, токи могут быть большими Токи Фуко используют: 1. Вакуумная плавка 2. Обезгаживание в вакууме 3. Успокоение подвижных частей приборов Затухание маятника Токи Фуко вредны: В трансформаторах - греется сердечник. Чтобы преодолеть – сердечник делают из тонких пластин. (высокое между пластинами) Ферриты – материалы с большим и

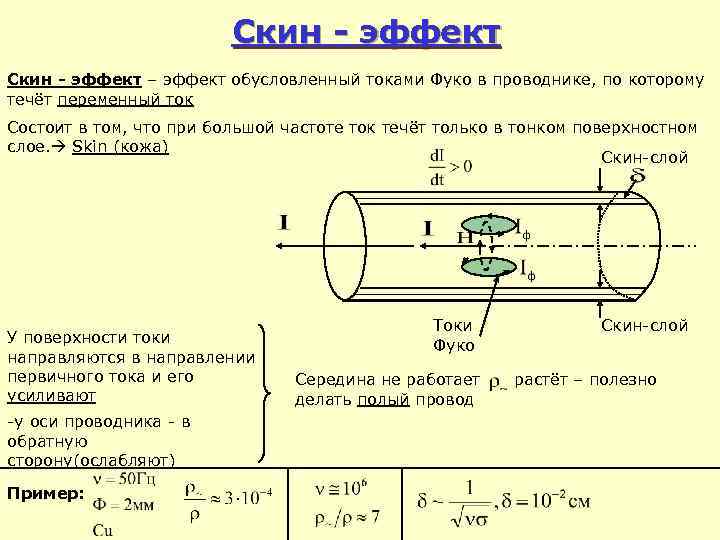Скин - эффект – эффект обусловленный токами Фуко в проводнике, по которому течёт переменный ток Состоит в том, что при большой частоте ток течёт только в тонком поверхностном слое. Skin (кожа) Скин-слой У поверхности токи направляются в направлении первичного тока и его усиливают -у оси проводника - в обратную сторону(ослабляют) Пример: Токи Фуко Середина не работает делать полый провод Скин-слой растёт – полезно