Электродинамика Список рекомендуемой литературы n n

Электродинамика

Список рекомендуемой литературы: n n n n Матвеев А. Н. Электродинамика. – М. : Высшая школа, 1980. Джексон Дж. Классическая электродинамика. –М. : Мир, 1965. Терлецкий Я. Л. , Рыбаков Ю. П. Электродинамика. –М. : Высшая школа, 1990. Топтыгин И. Н. Современная электродинамика. –М. : Институт компьютерных исследований, 2002. Власов А. А. Макроскопическая электродинамика. –М. : ФИЗМАТЛИТ, 2003. Тамм И. Е. Основы электричества. –М. : ФИЗМАТЛИТ, 2003. Батыгин В. В. , Топтыгин И. Н. Сборник задач по электродинамике. –М. : НИЦ Регулярная и хаотическая динамика, 2002.

Лекция 1 1. 1 Электродинамика и научно-технический прогресс 1. 2 Физические поля 1. 3 Дифференциальные характеристики физических полей

1. 1 Электродинамика и научно-технический прогресс Электродинамика - наука об электромагнитном поле и его связи с электрическими зарядами, а также о действии поля на заряды. n n n Основной объект, изучаемый электродинамикой - не заряд, а электромагнитное поле - переносчик электромагнитного взаимодействия. Электромагнитное поле - реальный физический объект, вид материи, существующий в природе наряду с веществом. Все электромагнитные излучения, фиксируемые и используемые человеком, возникают за счет движения электрических зарядов, но существуют в вакууме самостоятельно.

На сегодняшний день в физике известны 4 типа взаимодействий, существующих в природе: n n 1) Гравитационное: универсально: в нем участвуют все тела в природе — от звезд, планет и галактик до микрочастиц: атомов, электронов, ядер. Его радиус действия равен бесконечности. Однако как для элементарных частиц микромира, так и для окружающих нас предметов макромира силы гравитационного взаимодействия настолько малы, что ими можно пренебречь. Оно становится заметным с увеличением массы взаимодействующих тел и потому определяющим в поведении небесных тел и образовании и эволюции звезд. 2) Слабое: Слабое взаимодействие присуще всем элементарным частицам, кроме фотона. Оно отвечает за большинство ядерных реакций распада и многие превращения элементарных частиц. 3) Электромагнитное: определяет структуру вещества, связывая электроны и ядра в атомах и молекулах, объединяя атомы и молекулы в различные вещества. Оно определяет химические и биологические процессы. Электромагнитное взаимодействие является причиной таких явлений, как упругость, трение, вязкость, магнетизм и составляет природу соответствующих сил. На движение макроскопических электронейтральных тел оно существенного влияния не оказывает. 4) Сильное: Сильное взаимодействие осуществляется между адронами, именно оно удерживает нуклоны в ядре.

Скаляр- однокомпонентная величина, значение, которой не зависит от выбора системы координат. Примеры: масса, энергия, заряд, работа, плотность, объем, давление. Вектор - трехкомпонентная величина , компоненты которой преобразуются при поворотах системы координат как компоненты радиус-вектора Примеры: сила, скорость, ускорение, напряженность электрического поля. Правая декартова координатная система – три взаимно перпендикулярные координатные оси x, y, z, Правая декартова координатная система – три взаимно перпендикулярные координатные оси направленные так, что направление оси z определяется направлениями осей x, y по правилу правого винта. Единичные орты – три единичных вектора ( ), направленные по соответствующим координатным осям. Линейная комбинация векторов - , где , - вещественные числа. ЛКВ обладает всеми Линейная комбинация векторов - , где , традиционными алгебраическими свойствами суммы произведений. Скалярное произведение векторов - скаляр, со следующими свойствами: 1. 2. 3. Векторное произведение векторов - вектор, со следующими свойствами: Векторное произведение векторов - 1. 2. Модуль векторного произведения – это площадь параллелограмма, построенного на векторах-сомножителях.

Смешанное произведение векторов: - скаляр, модуль которого равен объему параллелепипеда, построенного на векторах-сомножителях. Для любых векторов СПВ не меняется при их циклической перестановке и меняет знак при перестановке двух любых векторов-сомножителей. Некоторые сведения из алгебры векторов:

1. 2 Физические поля Физическое поле- это особая форма материи, существующая в каждой точке пространства проявляющаяся воздействием на вещество, обладающее свойством, родственным с тем, которое создало это поле. Свойства физических полей: 1. Вещество имеет всегда резкую границу того объема, который оно занимает, а поле принципиально не может иметь резкой границы, оно изменяется плавно от точки к точке. 2. В одной точке пространства может существовать бесконечное количество физических полей, не влияющих друг на друга. Математическая классификация полей Электромагнитное поле - это особая форма материи, характеризующаяся значением векторов E и H в каждой точке пространства. Скалярное поле – это особая форма материи, характеризующая одним единственным числомскаляром . Векторное поле - это особая форма материи, характеризующаяся непрерывной векторной величиной с областью определения. Основной характеристикой этого поля является векторная линия. Это линия, в каждой точки которой вектор поля направлен по касательной.

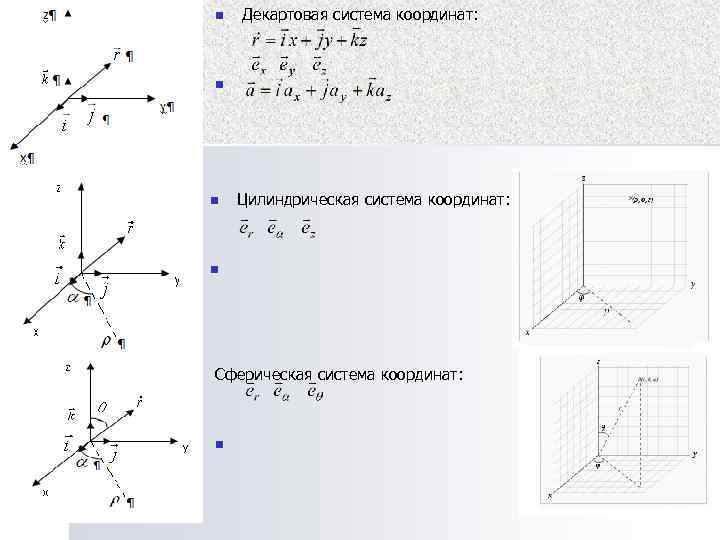n Декартовая система координат: n Цилиндрическая система координат: n Cферическая система координат: n

1. 3 Дифференциальные характеристики физических полей Компоненты вектора R

Градиент- векторная характеристика скалярного поля. Градиент скалярной функции – вектор, численно равный производной от этой функции по направлению нормали к поверхности уровня и направленный по этой нормали. Градиент-скорость пространственного изменения скалярной величины, каждая его компонента показывает скорость изменения вектора по соответствующей координате. Он ориентирован в том направлении, где имеет самую длинную проекцию. Свойства градиента: 1) численно равен максимальной скорости изменения функции. 2) его направление совпадает с направлением быстрейшего изменения функции. - Это не число, это оператор, вектор - не жаждущий оператор

Комбинация с вектором Дивергенция - скалярная характеристика векторного поля. Она характеризует наличие или отсутствие в какой-то точке поля источников (где поле начинается и заканчивается). Если в какой-то точке дивергенция положительна, то в этой точке находится исток поля, то есть его начало, там, где поле заканчивается, дивергенция отрицательна и это точка называется стоком. В точке, где нет источников, дивергенция равна нулю.

Ротор – векторная характеристика векторного поля. Он характеризует способность поля к образованию вихрей, замыканию векторных линий. Если в какой-то точке ротор равен нулю, то в этой точке находится вихрь или замкнутая силовая линия. Оператор Лапласа Итак, имеем 3 сорта комбинаций