Электричество и магнетизм Храмов Владимир Николаевич Мультимедийные лекции

Электричество и магнетизм Храмов Владимир Николаевич Мультимедийные лекции кафедры лазерной физики

ОСНОВНАЯ ЛИТЕРАТУРА для физических специальностей • Сивухин Д. В. Общий курс физики. В 5 томах. Т. 3. Электричество • Матвеев А. Н. Электричество и магнетизм • Калашников С. Г. Электричество для инженерно-технических специальностей • Савельев И. В. Курс общей физики. т. 2. Электричество и магнетизм. Оптика. Волны • Иродов И. Е. Основные законы электромагнетизма • Трофимова Т. И. Основы физики. Электродинамика • Трофимова Т. И. Курс физики

Структура дисциплины «Электричество и магнетизм» 1. Электростатическое поле 2. Теорема Гаусса для электростатического поля в вакууме 3. Электростатическое поле в диэлектриках 4. Проводники в электростатическом поле 5. Законы постоянного тока 6. Классическая теория электропроводности металлов 7. Электрический ток в жидкостях и газах 8. Магнитное поле в вакууме 9. Магнитное поле в веществе 10. Электромагнитная индукция 11. Уравнения Максвелла 12. Электромагнитные колебания

1. Электростатическо е поле Электростатика – раздел науки об электричестве, изучающий взаимодействие электрических зарядов, неподвижных относительно друга и систем координат.

Электрический заряд – физическая величина, определяющая интенсивность электрических взаимодействий. Электрический заряд – фундаментальное свойство материи. Единица измерения электрическ ого заряд а в СИ : 1 кулон ( Кл). 1 Кл – это электрический заряд, переносимый через поперечное сечение проводника за 1 с при силе тока в проводнике, равном 1 А.

Электрический заряд. Клe 19 106, 1 кгm p 27 1067, 1 Фундаментальные свойства электрического заряда 1. Существует в двух видах: положительный и отрицательный. 2. Одноименные заряды отталкиваются, разноименные – притягиваются. 3. Электрический заряд инвариантен. Его величина не зависит от системы отсчета. 4. Электрический заряд дискретен. Заряд любого тела составляет целое кратное от элементарного электрического заряда Носитель – е : электрон Носитель + е : протон 5. Электрический заряд аддитивен. Заряд любой системы тел равен сумме зарядов тел, входящих в систему. кгm e 31 1011,

Закон сохранения электрического заряда А лгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему, не изменяется при любых процессах, происходящих в этой системе. Электрически изолированная система – система, не обменивающаяся зарядами с внешними телами.

Закон Кулона ( 1785 г. ) Шарль Огюстен Кулон (1736 -1806) В ыдающийся французский физик и военный инженер , один из основателей электростатики Точечный заряд – заряд, сосредоточенный на теле, линейные размеры которого пренебрежимо малы по сравнению с расстояниями до других заряженных тел. Точечный заряд – физическая абстракция. 2 21 04 1 r qq F Сила взаимодействия F между двумя неподвижными точечными зарядами, находящимися в вакууме , пропорциональна зарядам q 1 и q 2 и обратно пропорциональна квадрату расстояния r между ними:

Сила Кулона направлена по прямой, соединяющей взаимодействующие заряды ( центральная сила ). F>0 – отталкивание (одноимённые заряды) F<0 – притяжение (разноименные заряды)rr qq 12 2 21 0 12 4 1 r F 2112 FF 1212 rr r Ф/м 1085, 8 12 0 м/Ф 109 4 1 9 0 Электрическая постоянная

Напряженность электростатического поля. Если в пространстве, окружающем заряд Q , находится другой заряд q , то на него действует кулоновская сила 2 04 1 r q. Q F Электрический заряд Q создает электрическое поле. Взаимодействие между покоящимися зарядами осуществляется через электрическое (электростатическое) поле. Электрическое поле – составная часть единого электромагнитного поля. Электромагнитное поле – особая форма материи, посредством которой осуществляются электромагнитные взаимодействия заряженных тел, в общем случае движущихся относительно данной системы отсчета.

Напряженность электростатического поляq F E Для обнаружения и исследования электростатического поля используется пробный точечный положительный заряд (который не искажает исследуемое поле). Напряженность электростатического поля в данной точке – физическая величина, определяемая силой, действующей на пробный единичный положительный заряд q , помещенный в эту точку поля: Единица напряженности электрического поля: 1 Н/Кл=1 В/м. Напряженность является силовой характеристикой электростатического поля.

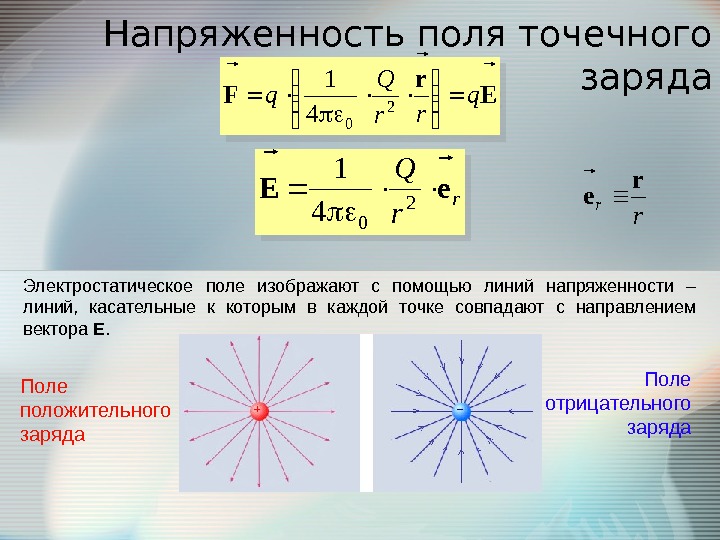
Напряженность поля точечного зарядаr r r e E r F q rr Q q 2 04 1 r r Q e. E 2 04 1 Электростатическое поле изображают с помощью линий напряженности – линий, касательные к которым в каждой точке совпадают с направлением вектора Е. Поле положительного заряда Поле отрицательного заряда

Принцип суперпозиции электростатических полей Напряженность Е результирующего поля в данной точке, создаваемого системой зарядов, равна векторной сумме напряженностей поле, которые создавал бы каждый из зарядов системы в отдельности: n i i

Примеры электростатических полей

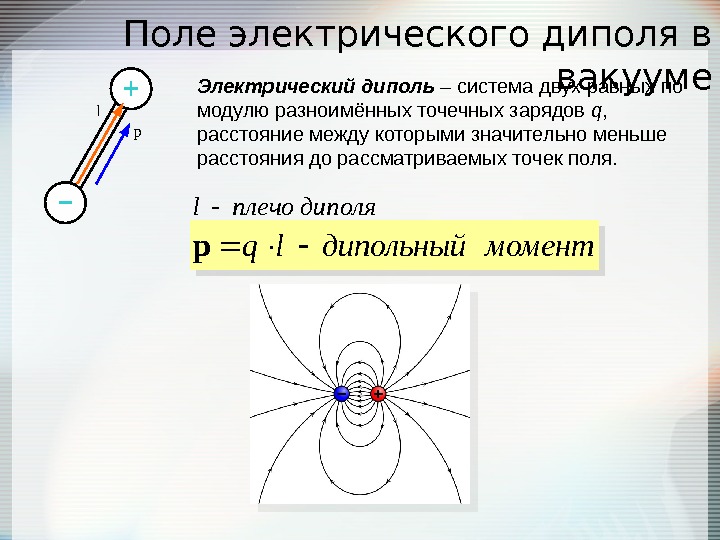
Поле электрического диполя в вакууме Электрический диполь – система двух равных по модулю разноимённых точечных зарядов q , расстояние между которыми значительно меньше расстояния до рассматриваемых точек поля. диполяплечоl моментдипольныйlq p

Напряженность поля на продолжении оси диполя r l

Напряженность поля на перпендикуляре к середине оси диполя

Циркуляция вектора напряженности электрического поля cos’ 4 1 cosdd 2 0 dl rqq ldl. A FF r rqq A o d’ 4 1 d 2 rldcosd. Пусть заряд q создает электростати-ческое поле. На заряд q’ действует кулоновская сила. Работа этой силы на элементарном перемещении: Работа при перемещении заряда q’ вдоль произвольной траектории из точки 1 в точку 2: 210 2 0 12 11 4 ‘d 4 ‘ d 2 12 1 rr qq r rqq AA r r Работа не зависит от траектории перемещения. Следовательно, электростатическое поле точечного заряда является потенциальным , а электростатические силы – консервативными.

Циркуляция вектора напряженности электрического поля Работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L равна нулю: L A 0 d dl. Eldl E cos. EEl LL ldl. Eld 0 E Работа сил поля на элементарном перемещении единичного заряда: — проекция вектора E на направление элементарного перемещения Теорема о циркуляции вектора напряженности Силовое поле Е называют потенциальным , если его циркуляция по любому замкнутому контуру равна нулю.

Потенциал электростатического поля ‘q. W 21 2112» WW r qq k. A const rqq k. W ‘ r qq W ‘ 4 1 0 n i i. WW 1 ‘q. W n i i 1 Работа сил электростатического поля: Потенциальная энергия заряда q’ в поле заряда q : r 0 WПри В поле нескольких зарядов: Потенциал – физическая величина, определяемая работой по перемещению единичного положительного заряда при удалении его из данной точки на бесконечность (единица в СИ: 1 Вольт). В поле нескольких зарядов: r q 0 4 1 ‘q A )(‘212112 q. WWAВ поле точечного заряда: Разность потенциалов двух точек в электростатическом поле определяется работой, совершаемой силами поля, при перемещении единичного положительного заряда из одной точки в другую:

Связь между напряженностью и потенциалом Wgrad. F grad. E Консервативная сила и потенциальная энергия связаны между собой соотношением: Напряженность поля и потенциал связаны между собой соотношением: 2 12 112 ddlql. A EF 2 121 dl

Эквипотенциальные поверхности

2. Теорема Гаусса для электростатическог о поля в вакууме

Поток вектора напряженности электростатического поля SE ddd SE n. E SS n. ESESE dd. Поток вектора напряженности сквозь площадку d S : [ В м ] Для произвольной замкнутой поверхности:

Теорема Гаусса для электростатического поля в вакууме 02 2 0 4 4 d q r rq SE S n. E i S i i SE Sd. ESE d n i i S q 1 01 d SE Поток вектора напряженности сквозь сферическую поверхность радиуса r , охватывающую точечный заряд q в ее центре: Этот результат справедлив для замкнутой поверхности любой формы. Для системы зарядов: Теорема Гаусса для электростатического поля в вакууме

Теорема Гаусса для электростатического поля в вакууме V q d d VS Vd 1 d 0 SE Теорема Гаусса для электростатического поля в вакууме. Объемная плотность заряда:

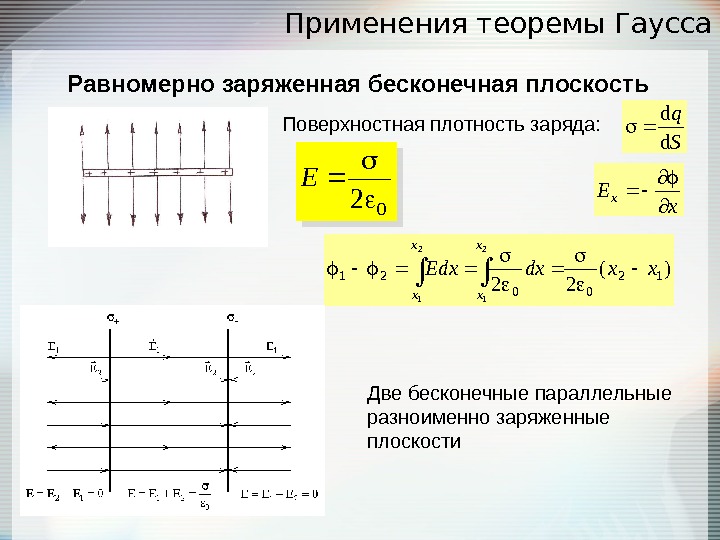
Применения теоремы Гаусса Равномерно заряженная бесконечная плоскость S q d d 02 Ex E x )( 22 12 0021 2 1 xxdx. Edx x xx x Поверхностная плотность заряда: Две бесконечные параллельные разноименно заряженные плоскости

Применения теоремы Гаусса Равномерно заряженная сферическая поверхность Пусть сферическая поверхность радиусом R равномерно заряжена зарядом Q с поверхностной плотностью заряда . 0 24 Q r. E Если r > R , то внутрь поверхности попадает весь заряд Q , создающий поле. По теореме Гаусса: )( 4 1 2 0 Rr r Q E Если r < R , то замкнутая поверхность не содержит внутри зарядов, поэтому здесь E = 0.

Применения теоремы Гаусса Равномерно заряженная сферическая поверхность Разность потенциалов между двумя точками на расстояниях r 1 от центра сферы ( r 2 > r 1 > R ): 2102 021 11 4 d 4 1 d 2 1 rr. Q r r Q r. E r rr r 21 rrr r Q 0 4 1 R Q 0 4 1 Если принять , то потенциал поля вне поверхности Внутри поверхности потенциал постоянный:

Применения теоремы Гаусса Объемно заряженный шар Пусть шар радиусом R равномерно заряжен зарядом Q с объемной плотностью заряда . 0 24 Q r. E Если r > R , то внутрь поверхности попадает весь заряд Q , создающий поле. По теореме Гаусса: )( 4 1 2 0 Rr r Q E (вне шара, как для сферы) Внутри шара сфера радиусом r’ < R охватывает заряд 3 )( 34 r. Q 0 3 02 )( 3 4 )(4 r. Q r. E 3 3 4 R Q )( 4 1 3 0 Rrr R Q E По теореме Гаусса:

Применения теоремы Гаусса Объемно заряженный шар Разность потенциалов между двумя точками на расстояниях r 1 от центра сферы ( r 2 > r 1 > R ): 2102 021 11 4 d 4 1 d 2 1 rr. Q r r Q r. E r rr r )( 4 1 3 0 Rrr R Q E Внутри шара 2/ 12/ 2 3 021 )()( 8 d /2 /1 rr RQ r. Er r

Применения теоремы Гаусса Равномерно заряженный бесконечный цилиндрl q d d Линейная плотность заряда: 1 2 00 21 ln 22 2 12 1 r r r dr Edr r r 0 2 l rl. E )( 2 1 0 Rr r. E По теореме Гаусса: Если r r 1 > R ):

3. Электростатическо е поле в диэлектриках

Типы диэлектриковм. Ом 1010 156 м)Ом 1010: металловдля(68 Диэлектриками называют вещества, которые при обычных условиях практически не проводят электрический ток. В диэлектриках нет свободных носителей зарядов — заряженных частиц, которые под действием электрического поля могли бы прийти в упорядоченное движение и образовать электрический ток проводимости. К диэлектрикам относятся все газы (если они не подверглись ионизации), некоторые жидкости и твердые тела. Удельное электрическое сопротивление диэлектриков: Особенности поведения таких веществ в электростатических полях объясняются, прежде всего, их молекулярным строением. Электрически заряженные элементарные частицы, входящие в состав молекул диэлектриков, достаточно прочно связаны друг с другом внутриатомными силами. Электрические заряды, входящие в состав атомов и молекул, а также заряды ионов в кристаллических диэлектриках с ионной решеткой, называются связанными зарядами. Заряды, не связанные с частицами вещества, называются свободными. Последние — это заряды частиц, способных перемещаться под действием электрического поля (свободные электроны в металлах и полупроводниках, ионы в электролитах и газах, электроны и ионы в плазме), положительные заряды ионов кристаллической решетки металлов, избыточные заряды, сообщенные проводящему телу.

Типы диэлектриков 1. Неполярные диэлектрики (диэлектрики с неполярными молекулами). В отсутствие внешнего электрического поля дипольный момент отсутствует. Под действием внешнего поля заряды смещаются в противоположные стороны ((+) по полю; (-) против поля и молекулы приобретают дипольный момент. Примеры : N 2 , H 2 , O 2 , CH 4 . 2. Полярные диэлектрики (диэлектрики с полярными молекулами). В отсутствие внешнего электрического поля есть дипольный момент. Дипольные моменты ориентированы хаотично. Под действием внешнего поля диполи поворачиваются вдоль поля. Возникает ненулевой результирующий дипольный момент. Примеры : H 2 O , NH 3 , SO 2 , CO . 3. Ионные диэлектрики. Ионные кристаллы имеют пространственные решетки с правильным чередованием ионов разных знаков: систему двух сдвинутых одна в другую ионных подрешеток. Под действием внешнего поля происходит деформация решетки, приводящая к относительному смещению подрешеток. Примеры : Na. Cl , KBr.

Поляризация диэлектриков – процесс ориентации диполей или появление под воздействием внешнего электрического поля ориентированных по полю диполей, в результате чего возникает отличный от нуля суммарный дипольный момент молекул диэлектрика. Виды поляризации 1. Электронная (деформационная) поляризация диэлектрика с неполярными молекулами 2. Ориентационная (дипольная) поляризация диэлектрика с полярными молекулам 3. Ионная поляризация диэлектриков с ионными кристаллическими решетками.

Поляризованность – векторная величина, характеризующая поляризацию диэлектрика, определяемая дипольным моментом единицы объема диэлектрика: VV i i V p p PEP 0 Для изотропных диэлектриков (кроме сегнетоэлектриков) и несильных полей: — диэлектрическая восприимчивость вещества

Поляризованность Нескомпенсированные заряды, появляющиеся в результате поляризации диэлектрика, называются связанными. Внесем в однородное внешнее электрическое поле Е 0 пластинку из однородного диэлектрика. Под действием поля диэлектрик поляризуется, т. е. происходит смещение зарядов. В результате этого на правой грани диэлектрика, обращенного к отрицательной плоскости, будет избыток положительного заряда с поверхностной плотностью + ‘, на левой — отрицательного заряда с поверхностной плотностью – ‘.

Поляризованность Так как поверхностная плотность связанных зарядов ‘ меньше плотности свободных зарядов плоскостей, то не все поле Е компенсируется полем зарядов диэлектрика: часть линий напряженности пройдет сквозь диэлектрик, другая же часть — обрывается на связанных зарядах. Следовательно, поляризация диэлектрика вызывает уменьшение в нем поля по сравнению с первоначальным внешним полем. Вне диэлектрика Е = Е 0. EEE 0 0 EE PSd. PVp. V Sp. V P EEE 0 00 1 EE E 1 Появление связанных зарядов приводит к возникновению дополнительного поля Е ’ связанных зарядов, направленного против внешнего поля E 0. Поле внутри диэлектрика: Найдем поверхностную плотность связанных зарядов. Диэлектрическая проницаемость среды

Электрическое смещение Вектор D не претерпевает разрыва на границе двух диэлектриков. Вектор Е претерпевает разрыв скачком на границе двух диэлектриков. Вектор электрического смещения [ Кл/м 2 ] EP 0 1 ED 0 PED 0 21 002 001 2202 2 0 2 1101 1 0 1 ; ; DD ED ED EDE E 0 E E Результирующее поле в диэлектрике описывается вектором напряженности Е , и потому он зависит от свойств диэлектрика. Вектором D описывается электростатическое поле, создаваемое свободными зарядами. Линии вектора Е могут начинаться и заканчиваться на любых зарядах — свободных и связанных, в то время как линии вектора D — только на свободных зарядах. Через области поля, где находятся связанные заряды, линии вектора D проходят не прерываясь.

Поток вектора электрического смещения сквозь площадку d S : SD n. Dddd. SD S n S DSDdd. SD Для произвольной замкнутой поверхности S поток вектора электрического смещения сквозь эту поверхность:

Теорема Гаусса для поля в диэлектрике n i свобi S n S QSD 1 dd. SD VS n S VSDddd. SD Поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов. В такой форме теорема Гаусса справедлива для электростатического поля как для однородной и изотропной, так и для неоднородной и анизотропной сред. В случае непрерывного распределения заряда в пространстве с объемной плотностью свободных зарядов :

Условия для поля на границе двух диэлектриков l. E 21 Рассмотрим связь между векторами Е и D на границе раздела двух однородных изотропных диэлектриков (диэлектрические проницаемости которых 1 и 2 ) при отсутствии на границе свободных зарядов. Построим вблизи границы раздела диэлектриков 1 и 2 небольшой замкнутый прямоугольный контур ABCDA длины l. Согласно теореме о циркуляции вектора Е : ABCDA ld 0 E (знаки интегралов по АВ и CD разные, так как пути интегрирования противоположны, а интегралы по участкам ВС и DA ничтожно малы). 21 EE ED 0 21 21 D D Тангенциальная составляющая вектора E одинакова по обе стороны границы раздела диэлектриков (не претерпевает скачка, является непрерывной). Тангенциальная составляющая вектора D на границе раздела двух диэлектриков претерпевает скачок.

Условия для поля на границе двух диэлектриков. На границе раздела двух диэлектриков построим прямой цилиндр ничтожно малой высоты, одно основание которого находится в первом диэлектрике, другое — во втором. Основания S настолько малы, что в пределах каждого из них вектор D одинаков. Согласно теореме Гаусса для поля в диэлектрике: Входя в диэлектрик с большей диэлектрической проницаемостью, линии Е и D удаляются от нормали. 0 21 SDSD nn 21 nn DD 1 2 2 1 n n E E 1 2 11 22 1 2 // nn EE EE tgtg. Нормальная составляющая вектора D одинакова по обе стороны границы раздела диэлектриков (не претерпевает скачка, является непрерывной). Нормальная составляющая вектора E на границе раздела двух диэлектриков претерпевает скачок.

Сегнетоэлектрики — диэлектрики, обладающие в определенном интервале температур спонтанной ( самопроизвольной ) поляризованностью (поляризованностью в отсутствие внешнего электрического поля). Примеры : сегнетова соль Na. KC 4 H 4 O 6 • 4 Н 2 О ; титанат бария Ва. Т i. O 3 ; дигидрофосфат калия KH 2 PO 4. Домены – области с различными направлениями поляризованности.

Сегнетоэлектрики Сегнетоэлектрические свойства сильно зависят от температуры. Для каждого сегнетоэлектрика имеется определенная температура, выше которой его необычные свойства исчезают и он становится обычным полярным диэлектриком – точка Кюри. В сегнетоэлектриках вблизи точки Кюри наблюдается также резкое возрастание теплоемкости вещества. Превращение сегнетоэлектриков в обычный диэлектрик, происходящее в точке Кюри, сопровождается фазовым переходом II рода. Диэлектрическая проницаемость (а следовательно, и диэлектрическая восприимчивость) сегнетоэлектриков зависит от напряженности Е поля в веществе, а для других диэлектриков эти величины являются характеристиками вещества. Для сегнетоэлектриков связь между векторами поляризованности ( Р ) и напряженности ( Е ) нелинейная и зависит от значений Е в предшествующие моменты времени. В сегнетоэлектриках наблюдается явление диэлектрического гистерезиса ( «запаздывания» ). С увеличением напряженности Е внешнего электрического поляризованность Р растет, достигая насыщения (кривая 1 ). Уменьшение Р с уменьшением Е происходит по кривой 2 , и при Е= 0 сегнетоэлектрик сохраняет остаточную поляризованность Р 0 , т. е. сегнетоэлектрик остается поляризованным в отсутствие внешнего электрического поля. Чтобы уничтожить остаточную поляризованность, надо приложить электрическое поле обратного направления (— E с ). Величина Е c называется коэрцитивной силой (от лат. coercitio — удерживание). Если далее Е изменять, то Р изменяется по кривой 3 петли гистерезиса.

Пьезоэлектрики — кристаллические вещества, в которых при сжатии или растяжении в определенных направлениях возникает электрическая поляризация даже в отсутствие внешнего электрического поля ( прямой пьезоэффект ). Обратный пьезоэффект — появление механической деформации под действием электрического поля. У некоторых пьезоэлектриков решетка положительных ионов в состоянии термодинамического равновесия смещена относительно решетки отрицательных ионов, в результате чего они оказываются поляризованными даже без внешнего электрического поля. Такие кристаллы называются пироэлектриками. Электреты — диэлектрики, длительно сохраняющие поляризованное состояние после снятия внешнего электрического поля (электрические аналоги постоянных магнитов).

4. Проводники в электростатическо м поле

Проводники и распределение в них зарядов 0 E Проводники – тела, в которых электрический заряд может переме-щаться по всему их объему. Проводники первого рода – (металлы) – перенесение в них зарядов (свободных электронов) не сопровождается химическими превращениями. Проводники второго рода – (расплавленные соли, растворы кислот) – перенесение в них зарядов ((+) и (-)) ведет к химическим изменениям. При помещении проводников во внешнее электростатическое поле заряды в них начнут перемещаться, пока не установится равновесное распределение зарядов и электростатическое поле внутри проводника обращается в нуль: Т. к. grad. E , то потенциал во всех точках внутри проводника постоянен const n. EE Поверхность проводника в электростатическом поле – эквипотенциальная поверхность. Вектор Е направлен по нормали к каждой точке поверхности проводника:

Проводники и распределение в них зарядов SS n. SDQ 0 dd. SD Если проводнику сообщить заряд Q , то нескомпенсированные заряды располагаются только на поверхности проводника. Это следует непосредственно из теоремы Гаусса, согласно которой заряд Q, находящийся внутри проводника в некотором объеме, ограниченном произвольной замкнутой поверхностью, равен: так как во всех точках внутри поверхности D = 0. Найдем взаимосвязь между напряженностью Е поля вблизи поверхности заряженного проводника и поверхностной плотностью зарядов на его поверхности. Применим теорему Гаусса к бесконечно малому цилиндру с основаниями S , пересекающему границу проводник — диэлектрик. Ось цилиндра — вдоль вектора Е. Поток вектора D через внутреннюю часть цилиндрической поверхности равен нулю, так как внутри проводника Е 1 (а следовательно, и D 1 ) равен нулю, поэтому поток вектора D сквозь замкнутую цилиндрическую поверхность определяется только потоком сквозь наружное основание цилиндра. Согласно теореме Гаусса этот поток ( D S ) равен сумме зарядов ( Q = S ), охватываемых поверхностью: D S = S т. е. D 0 E — диэлектрическая проницаемость среды, окружающей проводник.

Проводники во внешнем электростатическом поле. Если во внешнее электростатическое поле внести нейтральный проводник, то свободные заряды (электроны, ионы) будут перемещаться: (+) — по полю, (-) — против поля. На одном конце проводника будет скапливаться избыток положительного заряда, на другом — избыток отрицательного. Эти заряды называются индуцированными. Процесс будет происходить до тех пор, пока E внутри проводника не станет равной нулю, а линии E вне проводника — перпендикулярными его поверхности. Нейтральный проводник, внесенный в электростатическое поле, разрывает часть линий напряженности; они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростатической индукцией. Индуцированные заряды появляются на проводнике вследствие смещения их под действием поля, т. е. является поверхностной плотностью смещённых зарядов. Электрическое смещение D вблизи проводника численно равно поверхностной плотности смещенных зарядов. Поэтому вектор D получил название вектора электрического смещения.

Электроемкость уединенного проводника Уединенный проводник – проводник, который удален от других проводников, тел и зарядов. Потенциал уединенного проводника пропорционален заряду Q , находящемуся на проводнике: CQ Q C — электрическая ёмкость (электроёмкость, емкость) уединенного проводника [C]= 1 Ф (фарада) ПРИМЕР. Электроемкость уединенного проводящего шара RQ dr r. Q Edr RR 00 4 1 R

Конденсаторы. Электроемкость конденсаторов Конденсатор – система из двух проводников (обкладок) с одинаковыми по модулю, но противоположными по знаку зарядами, форма и расположение которых таковы, что поле сосредоточено в узком зазоре между обкладками. Электроемкость конденсатора: Q

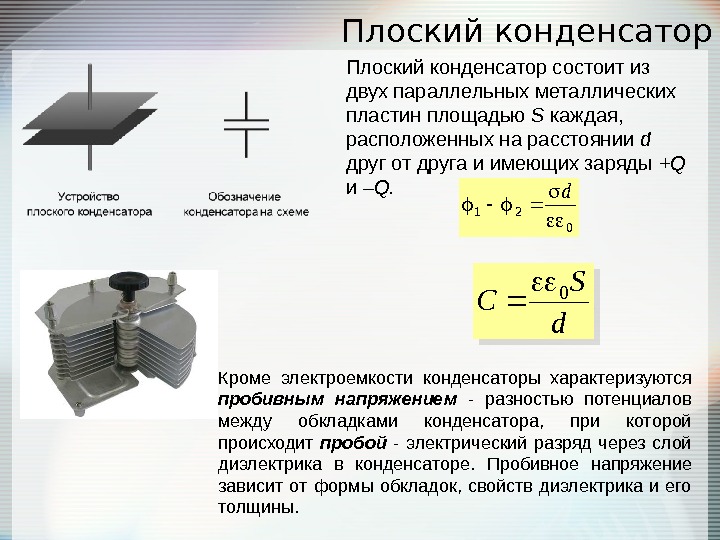
Плоский конденсатор 021 d d S C 0 Плоский конденсатор состоит из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды + Q и – Q. Кроме электроемкости конденсаторы характеризуются пробивным напряжением — разностью потенциалов между обкладками конденсатора, при которой происходит пробой — электрический разряд через слой диэлектрика в конденсаторе. Пробивное напряжение зависит от формы обкладок, свойств диэлектрика и его толщины.

Сферический конденсатор состоит из двух концентрических металлических обкладок, разделенных сферическим слоем диэлектрика. 21021 11 4 RR Q 21 21 04 RR RR C RRRRRRd 12112 то, )(Если d S d R C сф02 0 4 При малой величине зазора по сравнением с радиусом сферы выражения для емкости сферического и плоского конденсаторов совпадают.

Цилиндрический конденсатор 1 2 021 ln 2 RR l. Q RR 1 2 0 ln 2 RR l C Цилиндрический конденсатор состоит из двух полых коаксиальных цилиндров длиной l. — линейная плотность заряда

Соединения конденсаторов

Параллельное соединение конденсаторов nn CQ CQ CQ. . . . . 22 11 ). . . ( 21 1 nn i i CCCQQ n. CCC Q C . . . 21 n i i.

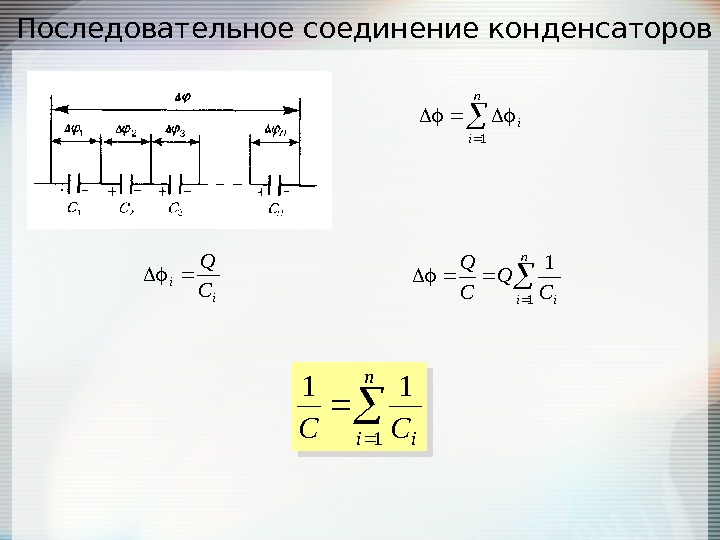
Последовательное соединение конденсаторов n i i 1 ii C Q n i i. CQ CQ 1 1 n i i.

Энергия заряженных проводников Энергия системы неподвижных точечных зарядов Найдем сначала потенциальную энергию системы двух неподвижных точечных зарядов Q 1 и Q 2 , находящихся на расстоянии r друг от друга. 21221211; QWQW r Q 1 0212 012 4 1 ; 4 1 WWW 21 212121 21 QQQQW n i ii QW 1 21 Общий случай: i – потенциал, создаваемый в точке нахождения заряда Q i всеми зарядами, кроме i -го

Энергия заряженных проводников Энергия уединенного заряженного проводника Чтобы увеличить заряд проводника на d Q , необходимо совершить работу по переносу этого заряда из бесконечности на проводник: d. Cd. Qd. A 2 2 0 C d. CA CQQC W 222 22 Полная работа:

Энергия заряженных проводников Энергия заряженного конденсатора Для перенесения заряда d Q с одной обкладки на другую внешние силы должны совершить работу: C Qd. Qd. A)( 21 C Qd. Q A Q 2 2 0 CQQC W 222 22 Полная работа:

Пондемоторная сила Найдем механическую (пондеромоторную) силу , с которой пластины плоского конденсатора притягивают друга. Для этого предположим, что расстояние х между пластинами меняется, например, на величину d x. Тогда действующая сила совершает работу d A = F d x вследствие уменьшения потенциальной энергии системы F d x = — d W , откуда. S Q dx d. W F 0 2 2 x S Q C Q W 0 22 22 Знак «минус» указывает, что сила F является силой притяжения.

Энергия электростатического поля Преобразуем формулу, выражающую энергию плоского конденсатора посредством зарядов и потенциалов, воспользовавшись выражением для емкости плоского конденсатора ( C = 0 S / d ) и разности потенциалов между его обкладками ( = Ed. Тогда где V = Sd — объем конденсатора. Формула показывает, что энергия конденсатора выражается через величину, характеризующую электростатическое поле, — напряженность Е. Объемная плотность энергии электростатического поля (энергия единицы объема) Выражение справедливо только для изотропного диэлектрика, для которого выполняется соотношение Р = 0 Е. V E Sd E W 22 2 02 0 22 2 0 EDE VW w

5. Законы постоянного тока

Электрический ток Электродинамика – раздел физики, в котором изучаются явления и процессы, обусловленные движением электрических зарядов или макроскопических заряженных тел. Электрический ток – любое упорядоченное (направленное) движение заряженных частиц или макроскопических тел ( носителей тока ). Ток проводимости – упорядоченное движение в среде или в вакууме свободных заряженных частиц (носителей тока). Конвекционный ток – перемещение в пространстве заряженного макроскопического тока. За направление электрического тока принимают движение положительных зарядов

Сила и плотность тока Количественной мерой электрического тока служит сила тока — скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени: t. Q I dd t. Q I S I j d d. Sne t Q I d d υj ne S d. I Sj Если сила тока и его направление не изменяются со временем, то такой ток называется постоянным : Q — электрический заряд, проходящий за время t через поперечное сечение проводника. Единица силы тока — ампер (А). Физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока, называется плотностью тока [ А/м 2 ] : Плотность тока — вектор , ориентированный по направлению тока, т. е. направление вектора j совпадает с направлением упорядоченного движения положительных зарядов: Сила тока сквозь произвольную поверхность S определяется как поток вектора j через эту поверхность: (если концентрация носителей тока равна n и каждый носитель имеет элементарный заряд е)

Сторонние силы. Электродвижущая сила (ЭДС) и напряжение Если в цепи на носители тока действуют только силы электростатического поля , то происходит перемещение носителей (+) от точек с большим потенциалом к точкам с меньшим потенциалом. Это приведет к выравниванию потенциалов во всех точках цепи и к исчезновению электрического поля. Для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счет работы сил неэлектростатического происхождения. Такие устройства называются источниками тока. Силы неэлектростатического происхождения, действующие на заряды со стороны источников тока, называются сторонними. Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС) , действующей в цепи: 0 ст Q A ε

Сторонние силы. Электродвижущая сила (ЭДС) и напряжениеld. Qld. Aстст EF 0 ld стε E 0 Qстст. EF Сторонняя сила F ст , действующая на заряд Q 0 : Е ст — напряженность поля сторонних сил. Работа сторонних сил по перемещению заряда Q 0 на замкнутом участке цепи: ЭДС, действующая в замкнутой цепи, может быть определена как циркуляция вектора напряженности поля сторонних сил. Э. д. с. , действующая на участке 1 — 2 : 2 112 ld стε E На заряд Q 0 помимо сторонних сил действуют также силы электростатического поля F e = Q 0 E. Результирующая сила, действующая в цепи на заряд Q 0 : EEFFF стст. Q 0 Работа, совершаемая результирующей силой над зарядом Q 0 на участке 1 — 2 : 2 1 12 ld. EQAстo

Сторонние силы. Электродвижущая сила (ЭДС) и напряжение 21012012 QQA ε 12012 εQA 122112 )(εUДля замкнутой цепи работа электростатических сил равна нулю, поэтому Работа, совершаемая результирующей силой над зарядом Q 0 на участке 1 — 2 : Напряжением U на участке 1 — 2 называется физическая величина, определяемая работой, совершаемой суммарным полем электростатических (кулоновских) и сторонних сил при перемещении единичного положительного заряда на данном участке цепи: Понятие напряжения является обобщением понятия разности потенциалов: напряжение на концах участка цепи равно разности потенциалов в том случае, если на этом участке не действует ЭДС, т. е. сторонние силы отсутствуют.

Сопротивление и проводимость проводников. Электрическое сопротивление R проводника – величина, характеризующая сопротивление проводника или электрической цепи электрическому току. Единица в СИ: 1 Ом Для однородного линейного проводника сопротивление R прямо пропорционально его длине l и обратно пропорционально площади его поперечного сечения S : S l R — удельное электрическое сопротивление (характеристика вещества) – физическая величина, определяемая электрическим сопротивлением однородного линейного проводника единичной длины и единичной площади поперечного сечения. Единица в СИ: 1 Ом м Материал , н. Ом м Серебро 16 Вольфрам 55 Медь 17 Никель 70 Алюминий 26 Нихром

Сопротивление и проводимость проводников Электрическая проводимость проводника (единица в СИ: симменс ( См )): R G 1 Удельная электрическая проводимость 1 (единица в СИ: См/м ): В первом приближении изменение удельного сопротивления, с температурой описывается линейным законом: )1(0 t — температурный коэффициент сопротивления , для чистых металлов (при не очень низких температурах) близкий к 1/273 К – 1. и 0 — удельные сопротивления проводника при t °С и 0°С соответственно.

Закон Ома для однородного участка цепи. Участок цепи, на котором не действуют сторонние силы (участок, не содержащий источника ЭДС), называют однородным. Георг Симон Ом (1787 -1854) R U I Закон Ома для однородного участка цепи Сила тока I в однородном участке цепи прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению R этого участка цепи: Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления в закон Ома, получим l. U S I 1 Ej U / l = Е — напряженность электрического поля в проводнике, I / S = j — плотность тока Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора Е , то направления j и Е совпадают Закон Ома в дифференциальной форме

Закон Ома для неоднородного участка цепи. Участок цепи, на котором действуют сторонние силы (участок, содержащий источника ЭДС), называют неоднородным. ст. EEj Закон Ома в дифференциальной форме для неоднородного участка цепи 1221εIR Закон Ома для неоднородного участка цепи в интегральной форме (обобщенный закон Ома) Если электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, 1 = 2 ; тогда получаем закон Ома для замкнутой цепи : R I

Закон Ома для неоднородного участка цепи. В общем случае R 0 = r + R , где r — внутреннее сопротивление источника тока, R — сопротивление внешней цепи. Поэтому закон Ома для замкнутой цепи будет иметь вид Если цепь разомкнута и, следовательно, в ней ток отсутствует ( I = 0), то из закона Ома получим = 1 — 2 , т. е. ЭДС, действующая в разомкнутой цепи, равна разности потенциалов на ее концах. Следовательно, для того чтобы найти ЭДС источника тока, надо измерить разность потенциалов на его клеммах при разомкнутой цепи. Rr. I

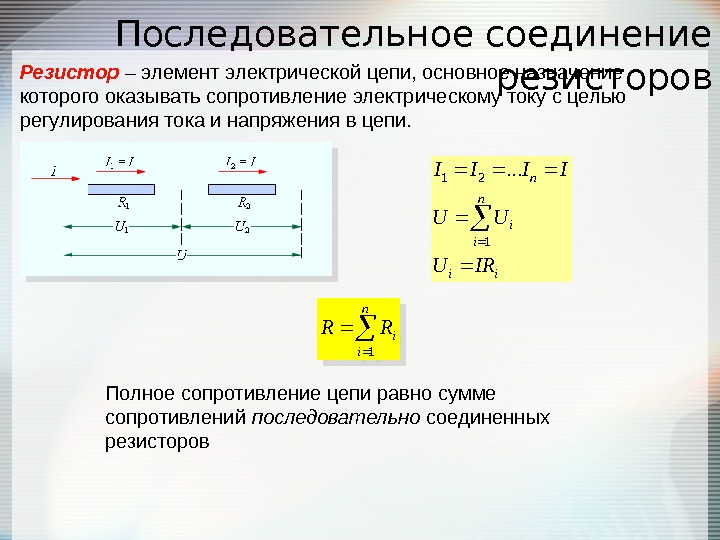
Последовательное соединение резисторов ii n i i n IRU UU IIII 121. . . Резистор – элемент электрической цепи, основное назначение которого оказывать сопротивление электрическому току с целью регулирования тока и напряжения в цепи. n i i. RR 1 Полное сопротивление цепи равно сумме сопротивлений последовательно соединенных резисторов

Параллельное соединение резисторов ii n i i n RU I II UUUU 1 21. . . n i i. RR 1 11 Величина, обратная полному сопротивлению цепи, равна сумме величин, обратных сопротивлениям всех параллельно соединенных резисторов

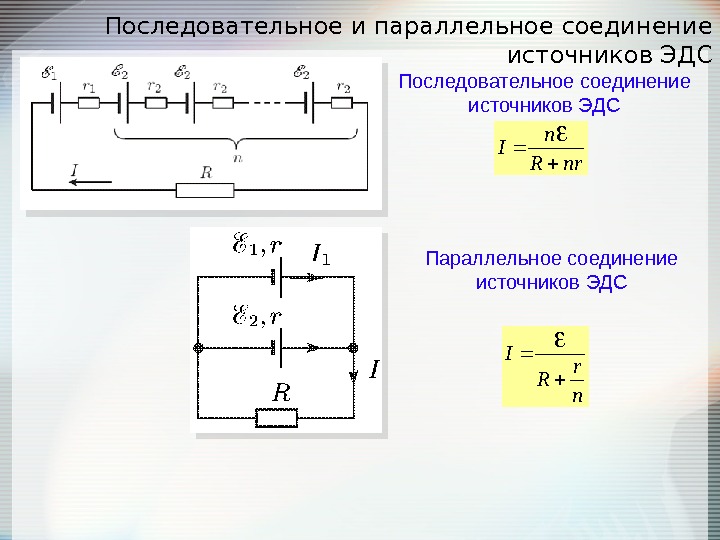
Последовательное и параллельное соединение источников ЭДС nr. R n I n r RI Последовательное соединение источников ЭДС Параллельное соединение источников ЭДС

Мощность тока. Закон Джоуля-Ленца IUdt. Udqd. A Рассмотрим однородный участок цепи, к которому приложено напряжение U. Силы электростатического поля и сторонние силы совершают работу по переносу заряда dq за время dt : Работа тока: IUdt. Udqd. A R U RIUI dt d. A P 2 2 d. Ad. Q dt R U Rdt. IIUdtd. Q 2 2 dt RU Rdt. Id. A 2 2 Мощность тока: Если ток идет по неподвижному проводнику и не происходит химических превращений, то вся работа идет на его нагревание Закон Джоуля-Ленца

Мощность тока. Закон Джоуля-Ленца t Rdt. IQ 0 2 2 jw 2 Ej. Ew. Закон Джоуля-Ленца в дифференциальной форме. Если сила тока изменяется со временем: Удельная тепловая мощность – количество теплоты выделяющаяся за единицу времени в единице объема

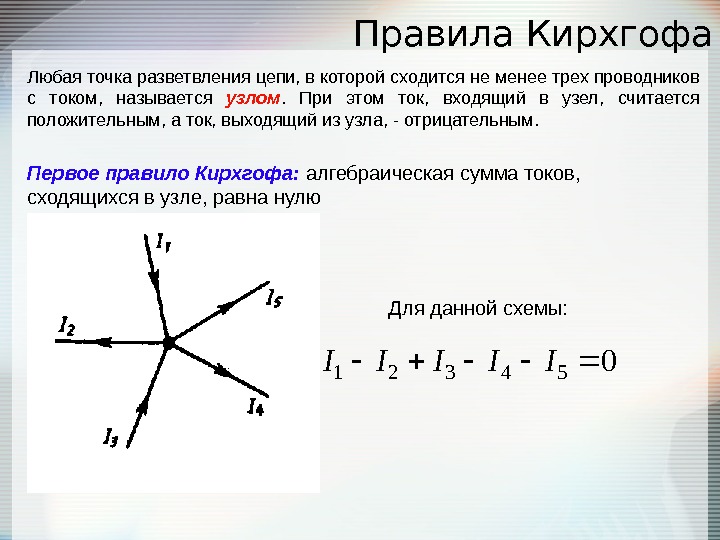
Правила Кирхгофа Любая точка разветвления цепи, в которой сходится не менее трех проводников с током, называется узлом. При этом ток, входящий в узел, считается положительным, а ток, выходящий из узла, — отрицательным. Первое правило Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю 0 54321 IIIII Для данной схемы:

Правила Кирхгофа Второе правило Кирхгофа : в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов I i на сопротивления R i соответствующих участков этого контура равна алгебраической сумме ЭДС , встречающихся в этом контуре n i iii. RI 11 Для данной схемы:

6. Классическая теория электропроводност и металлов

Элементарная классическая теория электропроводности металлов Носителями тока в металлах являются свободные электроны , т. е. электроны, слабо связанные с ионами кристаллической решетки металла. Это представление о природе носителей тока в металлах основывается на электронной теории проводимости металлов, созданной немецким физиком П. Друде (1863— 1906) и разработанной впоследствии нидерландским физиком X. Лоренцем, а также на ряде классических опытов, подтверждающих положения электронной теории. Опыт К. Рикке (1845— 1915) (1901) В течение года электрический ток пропускался через три последовательно соединенных с тщательно отшлифованными торцами металлических цилиндра (С u , А l ) одинакового радиуса. Несмотря на то что общий заряд, прошедший через эти цилиндры, достигал огромного значения ( 3, 5 10 6 Кл), никаких, даже микроскопических, следов переноса вещества не обнаружилось. Это явилось экспериментальным доказательством того, что ионы в металлах не участвуют в переносе электричества, а перенос заряда в металлах осуществляется частицами, которые являются общими для всех металлов. Такими частицами могли быть открытые в 1897 г. английским физиком Д. Томсоном (1856— 1940) электроны.

Элементарная классическая теория электропроводности металлов Для доказательства этого предположения необходимо было определить знак и величину удельного заряда носителей (отношение заряда носителя к его массе). Идея подобных опытов заключалась в следующем: если в металле имеются подвижные, слабо связанные с решеткой носители тока, то при резком торможении проводника эти частицы должны по инерции смещаться вперед, как смещаются вперед пассажиры, стоящие в вагоне при его торможении. Результатом смещения зарядов должен быть импульс тока; по направлению тока можно определить знак носителей тока, а зная размеры и сопротивление проводника, можно вычислить удельный заряд носителей. Идея этих опытов (1913) и их качественное воплощение принадлежат российским физикам С. Л. Мандельштаму (1879— 1944) и Н. Д. Папалекси (1880— 1947). Эти опыты в 1916 г. были усовершенствованы и проведены американским физиком Р. Толменом (1881— 1948) и ранее шотландским физиком Б. Стюартом (1828— 1887). Ими экспериментально доказано, что носители тока в металлах имеют отрицательный заряд, а их удельный заряд приблизительно одинаков для всех исследованных металлов. По значению удельного заряда носителей электрического тока и по определенному ранее Р. Милликеном элементарному электрическому заряду была определена их масса. Оказалось, что значения удельного заряда и массы носителей тока и электронов, движущихся в вакууме, совпадали. Таким образом, было окончательно доказано, что носителями электрического тока в металлах являются свободные электроны.

Элементарная классическая теория электропроводности металлов Теория Друде-Лоренца • В узлах кристаллической решетки располагаются ионы металла, а между ними хаотически движутся свободные электроны, образуя своеобразный электронный газ, обладающий, согласно электронной теории металлов, свойствами идеального газа. • Электроны проводимости при своем движении сталкиваются преимущественно не между собой, а с ионами решетки, в результате чего устанавливается термодинамическое равновесие между электронным газом и решеткой. • Электроны обладают такой же энергией теплового движения, как и молекулы одноатомного газа. em k. T u 8 При Т= 300 К u = 1, 1 10 5 м/с. Средняя тепловая скорость движения электронов: Тепловое движение электронов, являясь хаотическим, не может привести к возникновению тока.

Элементарная классическая теория электропроводности металлов При наложении внешнего электрического поля на металлический проводник кроме теплового движения электронов возникает их упорядоченное движение, т. е. возникает электрический ток. Среднюю скорость v упорядоченного движения электронов можно оценить согласно формуле для плотности тока: j = п e v . Оценка : Для медных проводов плотность тока ~ 10 7 А/м 2 , концентрация носителей тока n = 8 10 28 м – 3 . Средняя скорость упорядоченного движения электронов v ~ 7, 8 10 – 4 м/с. v << u При вычислениях результирующую скорость v + u можно заменять скоростью теплового движения u . Но замыкание электрической цепи влечет за собой распространение электрического поля со скоростью c = 3 10 8 м/с. Через время t = l / c ( l — длина цепи) вдоль цепи установится стационарное электрическое поле и в ней начнется упорядоченное движение электронов. Поэтому электрический ток возникает в цепи практически одновременно с ее замыканием.

Вывод закона Ома из классической теории электропроводности металлов Пусть в металлическом проводнике существует электрическое поле напряженностью E =const. Co стороны поля заряд е испытывает действие силы F = e. E и приобретает ускорение a = F / m = e. E / m. Во время свободного пробега электроны движутся равноускоренно, приобретая к концу свободного пробега скоростьm te. E max t — среднее время между двумя последовательными соударениями электрона с ионами решетки В конце свободного пробега электрон, сталкиваясь с ионами решетки, отдает им накопленную в поле энергию, поэтому скорость его упорядоченного движения становится равной нулю. Средняя скорость направленного движения электрона m te. E 22 0 max

Вывод закона Ома из классической теории электропроводности металлов u l t um le. E 2 E um lne nej 2 2 um lne 2 2 Классическая теория металлов не учитывает распределения электронов по скоростям, поэтому среднее время t свободного пробега определяется средней длиной свободного пробега l и средней скоростью движения электронов относительно кристаллической решетки проводника Средняя скорость направленного движения электрона Закон Ома в дифференциальной форме Удельная проводимость материала Ej

Вывод закона Джоуля-Ленца из классической теории электропроводности металлов 2 22 2 2 max 22 E um lem W K t me. E ta max lu z K Wznw 22 2 E un lne w 2 Ej. Ew (Закон Джоуля-Ленца в дифференциальной форме)К концу свободного пробега электрон под действием поля приобретает дополнительную кинетическую энергию При соударении электрона с ионом эта энергия полностью передается решетке и идет на увеличение внутренней энергии металла, т. е. на его нагревание. За единицу времени электрон испытывает с узлами решетки в среднем z столкновений Если n — концентрация электронов, то в единицу времени происходит п z столкновений и решетке передается энергия Удельная тепловая мощность тока

Закон Видемана-Франца Металлы обладают как большой электропроводностью, так и высокой теплопроводностью. Это объясняется тем, что носителями тока и теплоты в металлах являются одни и те же частицы — свободные электроны, которые, перемещаясь в металле, переносят не только электрический заряд, но и присущую им энергию хаотического (теплового) движения, т. е. осуществляют перенос теплоты. Эмпирический закон Видемана-Франца (1853 г. ): отношение теплопроводности ( ) к удельной проводимости ( ) для всех металлов при одной и той же температуре одинаково и увеличивается пропорционально термодинамической температуре: T 23 e k — постоянная, не зависящая от рода металла (k — постоянная Больцмана )

Трудности классической теории электропроводности металлов К лассическая теория электропроводности металлов хорошо объясн яет законы Ома и Джоуля — Ленца. Но по экспериментальному закон у Видемана — Франца = 3 ( k / e ) 2. Теория Лоренца дает = 2 ( k / e ) 2 что расхо дится с опытом. Температурная зависимость сопротивления. Из формулы удельной проводимости следует, что сопротивление металлов ( величина, обратно пропорциональная ) , должна возрастать пропорционально R ~ Т 1/2 , но эксперимент дает R ~ T. Оценка средней длины свободного пробега электронов в металлах. Чтобы по формуле получить , совпадающие с опытом, надо принимать l значительно больше истинных (предполагать, что электрон проходит без соударений с ионами решетки сотни междоузельных расстояний). Теплоемкость металлов. Теплоемкость металла складывается из теплоемкости его кристаллической решетки и теплоемкости электронного газа. Поэтому атомная (т. е. рассчитанная на 1 моль) теплоемкость металла по теории Друде-Лоренца должна быть значительно большей , чем атомная теплоемкость диэлектриков. Согласно закону Дюлонга и Пти , теплоемкость одноатомного кристалла равна 3 R. Учтем, что теплоемкость одноатомного электронного газа равна 3 / 2 R. Тогда атомная теплоемкость металлов должна быть близка к 4, 5 R. Но опыт показывает, что она равна 3 R , т. е. для металлов, так же как и для диэлектриков , хорошо выполняется закон Дюлонга и Пти. Движение электронов в металлах подчиняется не законам классической механики, а законам квантовой механики и, следовательно, поведение электронов проводимости надо описывать не статистикой Максвелла — Больцмана, а квантовой статистикой.

Эмиссионные явления Работа, которую нужно затратить для удаления электрона из металла в вакуум, называется работой выхода. Причины возникновения работы выхода 1. Если е ¯ по какой-то причине удаляется из металла, то в том месте, которое е ¯ покинул, возникает избыточный положительный заряд и е ¯ притягивается к индуцированному им самим положительному заряду. 2. Отдельные е ¯ , покидая металл, удаляются от него на расстояния порядка атомных и создают тем самым над поверхностью металла «электронное облако» , плотность которого быстро убывает с расстоянием. Это облако вместе с наружным слоем положительных ионов решетки образует двойной электрический слой, поле которого подобно полю плоского конденсатора. Толщина этого слоя — нескольким межатомных расстояний (0, 1 – 1 нм). Он не создает электрического поля во внешнем пространстве, но препятствует выходу свободных электронов из металла.

Эмиссионные явления Испускание электронов веществом при сообщении ему в результате внешних воздействий энергии, достаточной для преодоления работы выхода, называется электронной эмиссией. Виды электронной эмиссии 1. Термоэлектронная эмиссия – испускание электронов нагретыми металлами. 2. Фотоэлектронная эмиссия – эмиссия электронов из металла под действием света. 3. Вторичная электронная эмиссия – испускание электронов поверхностью мишени при ее бомбардировке пучком электронов. 4. Автоэлектронная эмиссия — эмиссия электронов с поверхности металла под действием сильного внешнего электрического поля.

7. Электрический ток в жидкостях и газах

Электрический ток в электролитах Чистые жидкости, например, дистиллированная вода, не проводят электрический ток, т. к. состоят из нейтральных атомов и молекул. Растворы кислот, щелочей и солей в воде и в других жидкостях проводят ток. Вещества, растворы которых проводят электрический ток, называются электролитами. В них прохождение тока всегда сопровождается химическими превращениями. Электролиты обладают ионной проводимостью. Носителями тока в них являются положительно и отрицательно заряженные ионы. Молекулы растворенного вещества диссоциируют – распадаются на ионы. Диссоциация молекул происходит независимо от наличия внешнего электрического поля. Степень диссоциации – отношение числа молекул, распавшихся на ионы, к общему числу молекул данного вещества. Упорядоченное движение ионов происходит во внешнем электрическом поле, создаваемом электродами – проводниками, соединенными с источником ЭДС. Анод (А) (+) Анионы (-) перемещаются к аноду Катод (К) (-) Катионы (+) перемещаются к катоду

Электрический ток в электролитах Плотность электрического тока в электролите: jjj vjvj n. Q Ev. Ev bb Ej bn. QЗакон Ома для электролитов: b + и b — — подвижности ионов(выражаются через заряды, концентрации и средние скорости упорядоченного движения положительных и отрицательных ионов в электрическом поле)

Законы электролиза (законы Фарадея) Электролизом называется выделение на электродах первичных или вторичных продуктов разложения раствора при прохождении через него электрического тока. Пример. 4422 SOHSOH k. Qm k. Itm n M Fn A e. N k A 11 Q n N F m 1 Кл 10602, 1 19 AN F e. Первый закон Фарадея Второй закон Фарадея Объединенный закон Фарадея. Масса вещества m , выделившегося на электроде, пропорциональна заряду Q , прошедшему через электролит. k – электрохимический эквивалент вещества Электрохимические эквиваленты веществ прямо пропорциональны их химическим эквивалентам. Химический эквивалент M/n – отношение молярной массы М иона к его валентности n. Кл/моль106484, 94 e. NFA — постоянная Фарадея

Электропроводность газов Газы при не слишком высоких температурах и при давлениях, близких к атмосферному, являются хорошими изоляторами. Газ становится проводником электричества, когда некоторая часть его молекул ионизуется , т. е. произойдет расщепление нейтральных атомов и молекул на ионы и свободные электроны. Для этого газ надо подвергнуть действию какого-либо ионизатора. При ионизации газов происходит вырывание из электронной оболочки атома или молекулы одного или нескольких электронов, что приводит к образованию свободных электронов и положительных ионов. Электроны могут присоединяться к нейтральным молекулам и атомам, превращая их в отрицательные ионы. Следовательно, в ионизованном газе имеются положительные и отрицательные ионы и свободные электроны. Прохождение электрического тока через газы называется газовым разрядом.

Электропроводность газов Основные ионизаторы: сильный нагрев короткое электромагнитное излучение (ультрафиолетовое, рентгеновское и -излучения) корпускулярное излучение (потоки электронов, протонов, -частиц) Для того чтобы выбить из молекулы (атома) один электрон, необходимо затратить определенную энергию, называемую энергией ионизации , значения которой для атомов различных веществ лежат в пределах 4 25 э. В. Одновременно с процессом ионизации газа всегда идет и обратный процесс — процесс рекомбинации : положительные и отрицательные ионы, положительные ионы и электроны, встречаясь, воссоединяются между собой с образованием нейтральных атомов и молекул. Чем больше ионов возникает под действием ионизатора, тем интенсивнее идет и процесс рекомбинации.

Несамостоятельный газовый разряд 0 en. Iнас Цепь содержит газовый промежуток, подвергающийся непрерывному , постоянному по интенсивности воздействию ионизатора. В результате действия ионизатора газ приобретает некоторую электропроводность и в цепи потечет ток. Разряды, существующие только под действием внешних ионизаторов, называются несамостоятельными.

Самостоятельный газовый разряд Разряд в газе, сохраняющийся после прекращения действия внешнего ионизатора, называется самостоятельным. Участок CD – ударная ионизация. Ударная ионизация под действием е — недостаточна для поддержания разряда при удалении внешнего ионизатора. Для этого необходимо, чтобы электронные лавины «воспроизводились» , т. е. чтобы в газе под действием каких-то процессов возникали новые е -.

Самостоятельный газовый разряд Процессы для поддержания самостоятельного разряда: ускоренные полем положительные ионы, ударяясь о катод, выбивают из него е — ; положительные ионы, сталкиваясь с молекулами газа, переводят их в возбужденное состояние; переход таких молекул в нормальное состояние сопровождается испусканием фотона; фотон, поглощенный нейтральной молекулой, ионизирует ее, происходит процесс фотонной ионизации молекул ; выбивание е — из катода под действием фотонов. При значительных напряжениях между электродами газового промежутка наступает момент, когда положительные ионы, обладающие меньшей длиной свободного пробега, чем электроны, приобретают энергию, достаточную для ионизации молекул газа, в к отрицательной пластине устремляются ионные лавины. Когда возникают кроме электронных лавин еще и ионные, сила тока растет уже практически без увеличения напряжения (участок DE ). Напряжение, при котором возникает самостоятельный разряд, называется напряжением пробоя.

Самостоятельный газовый разряд Типы самостоятельного разряда 1. Тлеющий разряд 2. Искровой разряд 3. Дуговой разряд 4. Коронный разряд

Тлеющий разряд 1 – положительный столб 2 – тлеющее свечение 3 – первое катодное свечение (катодная пленка) 4 – астоново темное пространство 5 – катодное темное пространство 6 – фарадеево темное пространство

Искровый разряд

Дуговой разряд

Коронный разряд

Плазма и ее свойства Плазмой называется сильно ионизованный газ, в котором концентрации положительных и отрицательных зарядов практически одинаковы. Различают высокотемпературную плазму , возникающую при сверхвысоких температурах, и газоразрядную плазму , возникающую при газовом разряде. Плазма характеризуется степенью ионизации — отношением числа ионизованных частиц к полному их числу в единице объема плазмы. В зависимости от величины говорят о слабо ( составляет доли процента), умеренно ( — несколько процентов) и полностью ( близко к 100%) ионизованной плазме. Условие существования плазмы : некоторая минимальная плотность заряженных частиц, начиная с которой можно говорить о плазме как таковой. Эта плотность определяется из неравенства L >> D , где L — линейный размер системы заряженных частиц, D — дебаевский радиус экранирования — расстояние, на котором происходит экранирование кулоновского поля любого заряда плазмы.

8. Магнитное поле в вакууме

Магнитное поле Подобно тому, как в пространстве, окружающем электрические заряды, возникает электростатическое поле, так и в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Наличие магнитного поля обнаруживается по силовому действию на внесенные в него проводники с током или постоянные магниты. Название «магнитное поле» связывают с ориентацией магнитной стрелки под действием поля, создаваемого током (X. Эрстед (1820 г. )). При пропускании через параллельные проводники токов однакового направления проводники притягиваются, при пропускании токов противоположного направления – отталкиваются (А. Ампер (1820 г. )). Магнитное поле создается только движущимися зарядами и действует только на движущиеся в этом поле электрические заряды.

Замкнутый плоский контур с током в магнитном поле Подобно тому, как при исследовании электростатического поля использовались точечные заряды, при исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), линейные размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле. Ориентация контура в пространстве определяется направлением нормали к контуру. Правило правого винта : за положительное направление нормали принимается направление поступательного движения винта, головка которого вращается в направлении тока, текущего в рамке. В однородном магнитном поле рамка с током не перемещается поступательно, а только поворачивается определенным образом. За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к свободно подвешенной рамке с током (или направление силы, которая действует на северный ( N ) полюс магнитной стрелки).

Магнитная индукция. Bp. M m np IS m m p M Bmax. Вращающий момент сил: P m – вектор магнитного момента рамки с током B – вектор магнитной индукции Для плоского контура с площадью S и током I : Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них действуют различные вращающие моменты, однако отношение М max /р m ( М max — максимальный вращающий момент) для всех контуров одно и то же и поэтому может служить характеристикой магнитного поля, называемой магнитной индукцией :