Электричество и магнетизм Фундаментальные свойства заряда 1

Электричество и магнетизм

Фундаментальные свойства заряда: 1) Электрический заряд существует двух видов – положительный и отрицательный. 2) В любой электрически изолированной системе алгебраическая сумма зарядов не изменяется – закон сохранения электрического заряда. 3) Электрический заряд является релятивистки инвариантным – его величина не зависит от системы отсчета, а значит, не зависит от того, движется он или покоится. Заряд всех элементарных частиц (если он не равен нулю) одинаков по абсолютной величине. +e – положительный заряд протона, -e – отрицательный заряд электрона. Точечные заряды – это заряженные тела, размеры которых малы по сравнению с расстояниями между ними, и в этом случае формой и размерами тел можно пренебречь.

Принцип суперпозиции (наложения) полей Результирующая сила, действующая на i-ый заряд равна векторной сумме сил от всех зарядов, действующих на пробный i-ый заряд

Напряженность электрического поля Всякий заряд изменяет свойства окружающего пространства – создает электрическое поле. Электростатическое поле - особая форма материи, посредством которой в пространстве и во времени взаимодействуют неподвижные электрические заряды. Напряженность электростатического поля в данной точке есть вектор, численно равный силе, действующей со стороны поля на единицу пробного заряда (положительного), помещенного в эту точку поля, и совпадающий по направлению с силой, действующей на заряд.

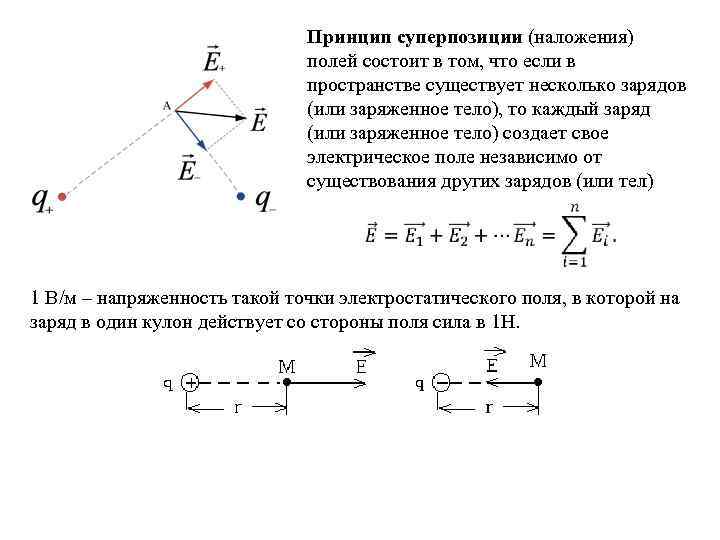Принцип суперпозиции (наложения) полей состоит в том, что если в пространстве существует несколько зарядов (или заряженное тело), то каждый заряд (или заряженное тело) создает свое электрическое поле независимо от существования других зарядов (или тел) 1 В/м – напряженность такой точки электростатического поля, в которой на заряд в один кулон действует со стороны поля сила в 1 Н.

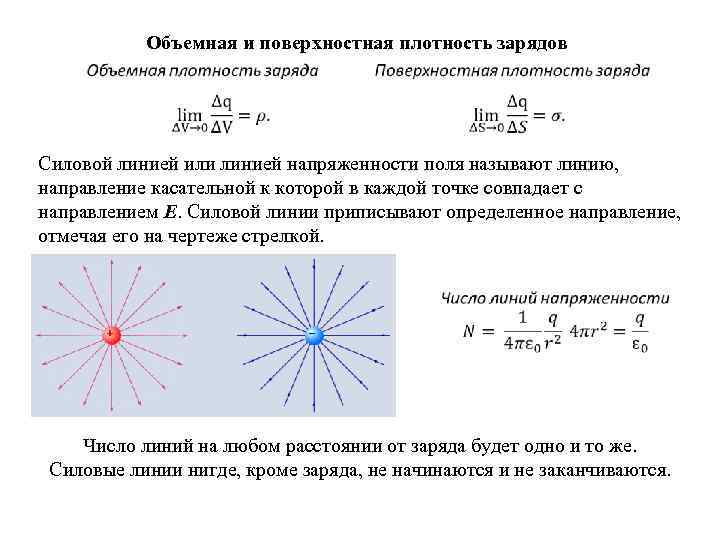Объемная и поверхностная плотность зарядов Силовой линией или линией напряженности поля называют линию, направление касательной к которой в каждой точке совпадает с направлением E. Силовой линии приписывают определенное направление, отмечая его на чертеже стрелкой. Число линий на любом расстоянии от заряда будет одно и то же. Силовые линии нигде, кроме заряда, не начинаются и не заканчиваются.

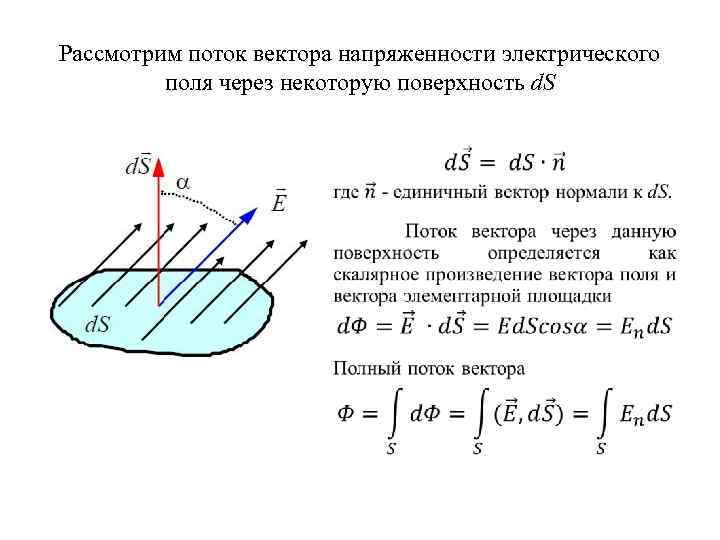Рассмотрим поток вектора напряженности электрического поля через некоторую поверхность d. S •

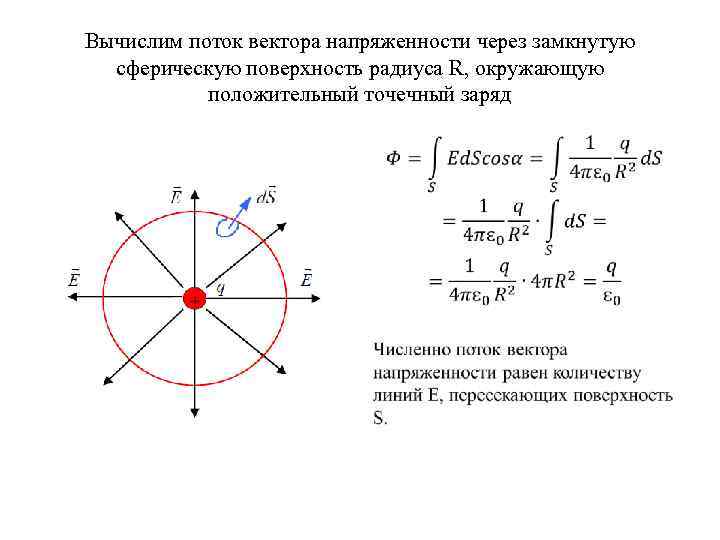Вычислим поток вектора напряженности через замкнутую сферическую поверхность радиуса R, окружающую положительный точечный заряд •

Пусть внутри некоторой замкнутой поверхности находится N точечных зарядов • Теорема Гаусса Поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме заключенных внутри поверхности зарядов, деленной на ԑ 0 •

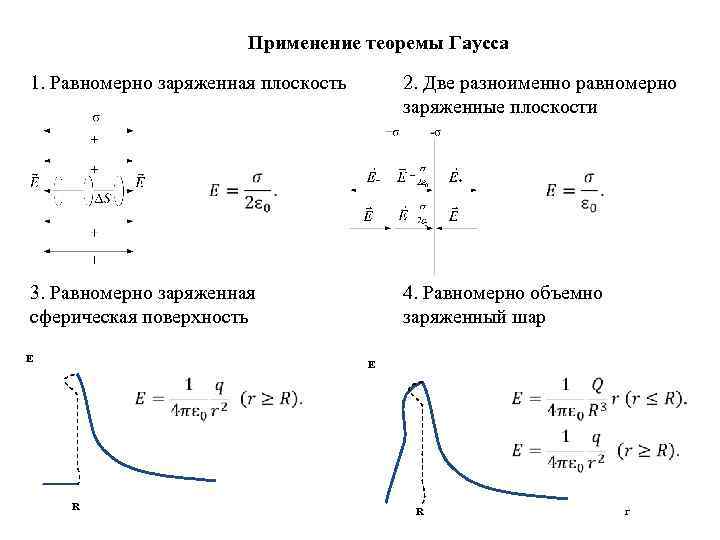Применение теоремы Гаусса 1. Равномерно заряженная плоскость 2. Две разноименно равномерно заряженные плоскости 3. Равномерно заряженная сферическая поверхность E 4. Равномерно объемно заряженный шар E R r

Работа в электростатическом поле В электростатическом поле, создаваемом зарядом q, из точки 1 в точку 2 перемещается заряд q'. Работа на пути dl равна Работа на всем пути 1 -2 будет равна Работа не зависит от пути, а только от начального и конечного положения заряда. Следовательно, силы, действующие на заряд q' в поле неподвижного заряда q являются потенциальными. Работа равна алгебраической сумме работ, совершаемых отдельными силами.

Тело, находящиеся в потенциальном поле сил, обладает потенциальной энергией, за счет которой совершается работа силами поля Потенциальная энергия заряда q' в поле заряда q Потенциал поля в данной точке Потенциал поля численно равен работе, которую совершают силы поля для над единичным положительным зарядом при удалении его из данной точки в бесконечность.

Заряд q, находящийся в точке поля с потенциалом φ, обладает потенциальной энергией Связь между напряженностью электрического поля и потенциалом Диполь в однородном и неоднородном электрических полях

Поляризация диэлектриков Диэлектрики обладают ничтожно малым количеством свободных носителей заряда и практически не проводят электрический ток. Поляризация – появление на поверхности диэлектрика поляризационных зарядов при внесении диэлектрика в электрическое поле. Диэлектрики Неполярные Полярные Ионные Тип Электронный поляризации Дипольный Ионный Сегнетоэлектрики Спонтанный В составе молекул и атомов имеются положительно заряженные ядра и отрицательно заряженные электроны. Для расстояний, больших по сравнению с размерами молекулы, действие всех электронов эквивалентно действию их суммарного заряда, помещенного в какую-то точку внутри молекулы, называемую центром тяжести отрицательных зарядов. Действие положительных зарядов внутри ядра также можно заменить действием суммарного положительного заряда, размещенного в центре тяжести положительных зарядов.

Молекула, у которой центры тяжести зарядов в отсутствии поля совмещены, называется неполярной молекулой. У полярной молекулы центры тяжести положительного и отрицательного зарядов смещены друг относительно друга, молекула в отсутствии поля обладает собственным дипольным моментом. Ионные кристаллы можно рассматривать как две решетки, вставленные одна в другую, одна из которых образована положительными ионами, другая отрицательными. Неполярные Полярные Под действием поля дипольные моменты полярных молекул устанавливаются вдоль поля. На величину дипольного момента внешнее поле практически не влияет. Полярная молекула ведет себя во внешнем электрическом поле как жесткий диполь. Ионные При помещении такого диэлектрика в электрическое поле обе решетки сдвигаются друг относительно друга, что приводит к поляризации диэлектрика.

Вектор поляризации – электрический момент единицы объема диэлектрика Вектор поляризации равен векторной сумме электрических моментов всех молекул, находящихся в единичном объеме. У диэлектриков (кроме сегнетоэлектриков) вектор поляризации связан с напряженностью поля в той же точке Для неполярных диэлектриков дипольный момент молекулы где n – число молекул в единице объема.

Описание поля в диэлектриках Электрическое смещение Безразмерную величину ԑ=1+ϰ называют относительной диэлектрической проницаемостью среды Относительная диэлектрическая проницаемость показывает, во сколько раз поле ослабляется внутри диэлектрика 1) Если однородный диэлектрик заполняет все пространство между двумя эквипотенциальными поверхностями, то напряженность поля внутри диэлектрика в ԑ раз меньше, чем напряженность поля свободных зарядов. 2) Учитывая п. 1, потенциал поля (и разность потенциалов, соответственно) уменьшается в ԑ раз. 3) При этом емкость конденсатора при заполнении его полностью диэлектриком увеличится в ԑ раз.

Сегнетоэлектрики. 1) Диэлектрическая проницаемость сегнетоэлектриков достигает нескольких тысяч единиц. 2) Зависимость P от E не является линейной. Диэлектрическая проницаемость сегнетоэлектриков зависит от напряженности поля. 3) При изменении поля значения вектора поляризации P отстают от напряженности поля E, в результате чего вектор P определяется не только величиной поля E в данный момент, но и от предшествующих значений поля E. 4) Сегнетоэлектрические свойства диэлектрика сильно зависят от температуры. Наличие точки (одной или нескольких) Кюри – температуры, выше которой сегнетоэлектрик ведет себя как нормальный диэлектрик.

Проводники в электрическом поле Для равновесия зарядов в проводнике должны соблюдаться следующие условия: 1) Напряженность поля внутри проводника в каждой точке должна быть равна нулю. Это означает, что потенциал внутри проводника должен быть постоянным. 2) Напряженность поля в каждой точке поверхности проводника должна быть направлена по нормали к поверхности. Замкнутый полый проводник экранирует только поле внешних зарядов

Электроемкость. Конденсаторы Потенциал уединенного проводника пропорционален заряду на проводнике Электроемкость Численно емкость равна заряду, сообщение которого проводнику повышает его потенциал на единицу. Единицей измерения емкости является фарада (Ф) – это емкость такого проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл. Емкость конденсатора – отношение заряда конденсатора к разности потенциалов между обкладками Емкость плоского конденсатора

Энергия электрического поля 1. Энергия системы зарядов 2. Энергия заряженного проводника 3. Энергия заряженного конденсатора 4. Энергия электрического поля Объемная плотность энергии

Соединение конденсаторов Параллельное соединение конденсаторов Последовательное соединение конденсаторов

Электрический ток – упорядоченный перенос электрических зарядов. Сила тока – заряд, переносимый через рассматриваемую поверхность в единицу времени Если в проводнике движутся носители тока обоих знаков, то сила тока где q- – абсолютная величина отрицательного заряда Вектор плотности тока j численно равен силе тока di через расположенную в данной точке перпендикулярную к направлению движения носителей заряда площадку d. S, отнесенную к величине этой площадки: За направление вектора плотности тока j выбирают направление движения положительно заряженных частиц (направление вектора скорости u+).

Пусть в единице объема имеется n+ положительных носителей и n- отрицательных. Если под действием поля они приобретают средние скорости u+ и u- соответственно, то за единицу времени через единичную площадку пройдет суммарный заряд где n+ – концентрация положительных носителей и n- отрицательных носителей заряда, e+ и |e-| – абсолютные величины зарядов носителей тока, ρ+ и ρ– – объемные плотности положительного и отрицательного носителей зарядов. Ток, не изменяющийся со временем, называют постоянным где q – заряд, переносимый через рассматриваемую поверхность за время t.

ЭДС Для поддержания тока необходимо от конца проводника с меньшим потенциалом перемещать заряды к концу проводника с большим потенциалом, т. е. совершать работу против сил электростатического поля. Перемещение зарядов на таких участках возможно лишь с помощью сторонних сил. Сторонние силы могут действовать как на всем протяжении цепи, так и на ее участках. Величину работы сторонних сил по перемещению единичного положительного заряда называют электродвижущей силой (ЭДС) Участок цепи, на котором не действуют сторонние силы, называется однородным. Участок цепи, на котором действуют сторонние силы, называется неоднородным. U – падение напряжения (или просто напряжение) на участке 1 -2.

Закон Ома для однородного участка цепи Закон Ома: сила тока, протекающего по однородному проводнику, пропорциональна разности потенциалов на его концах (напряжению U) Единицей сопротивления служит ом (Ом), равный сопротивлению такого проводника, в котором при напряжении 1 В течет ток 1 А. Сопротивление проводника цилиндрической формы с постоянным поперечным сечением ρ – удельное сопротивление вещества Закон Ома в дифференциальной форме σ – удельная электрическая проводимость среды

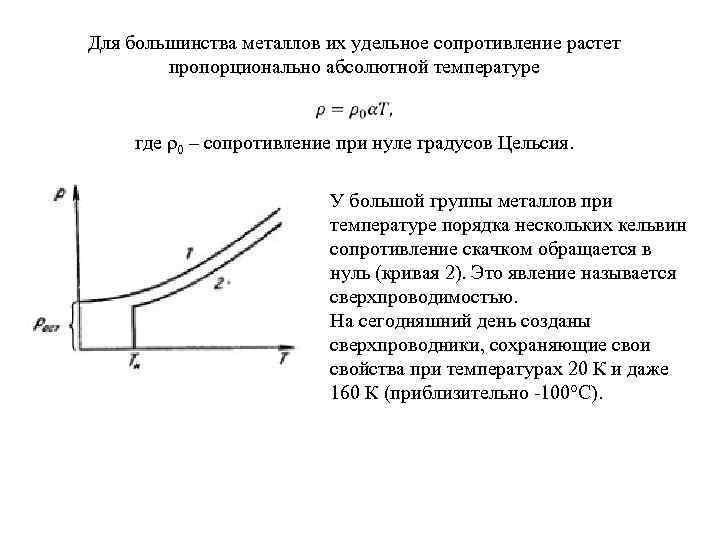Для большинства металлов их удельное сопротивление растет пропорционально абсолютной температуре где ρ0 – сопротивление при нуле градусов Цельсия. У большой группы металлов при температуре порядка нескольких кельвин сопротивление скачком обращается в нуль (кривая 2). Это явление называется сверхпроводимостью. На сегодняшний день созданы сверхпроводники, сохраняющие свои свойства при температурах 20 К и даже 160 К (приблизительно -100°С).

Закон Ома для неоднородного участка цепи где Ԑ - ЭДС, действующая в цепи, R – суммарное сопротивление всей цепи. Представим себе участок цепи, содержащий только источник ЭДС – между клеммами 1 и 2. Тогда в уравнении для выбранного участка цепи R – внутреннее сопротивление источника, а φ1 -φ2 – разность потенциалов на его клеммах. Когда источник разомкнут, то I=0 и Ԑ= φ2 - φ1, т. е. ЭДС источника можно определить как разность потенциалов на клеммах разомкнутого источника. Разность потенциалов на клеммах источника ЭДС, замкнутого на внешнее сопротивление, всегда меньше его ЭДС на величину падения напряжения на внешнем сопротивлении.

Разветвленные цепи. Правила Кирхгофа 1. Первое правило Кирхгофа. Узел цепи – точка, в которой сходится более чем два проводника. Ток, текущий к узлу, считается имеющим один знак (плюс или минус), текущий от узла – противоположный знак (минус или плюс). Первое правило Кирхгофа гласит, что алгебраическая сумма токов, сходящихся в узле, равна нулю Применительно к рисунку первое правило запишется так: I 1 – I 2 + I 3 = 0. Узел разветвленной цепи Уравнение, выражающее первое правило, можно записать для каждого из N узлов цепи, независимыми будут являться N-1 уравнение, N-е уравнение будет следствием из них.

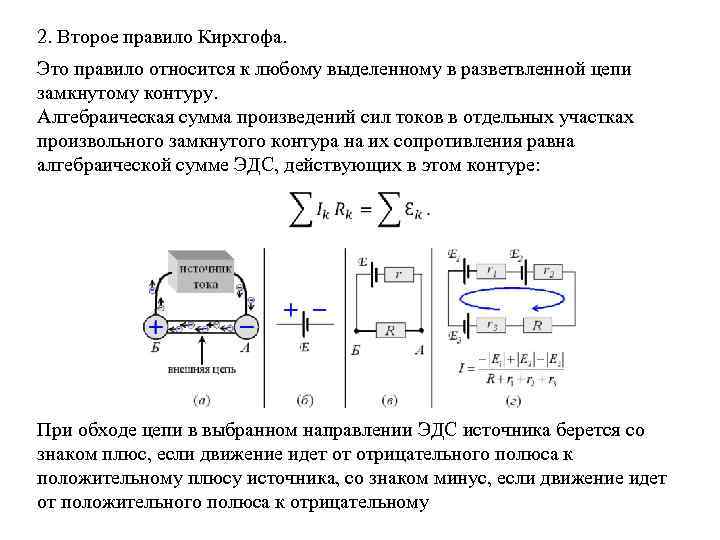2. Второе правило Кирхгофа. Это правило относится к любому выделенному в разветвленной цепи замкнутому контуру. Алгебраическая сумма произведений сил токов в отдельных участках произвольного замкнутого контура на их сопротивления равна алгебраической сумме ЭДС, действующих в этом контуре: При обходе цепи в выбранном направлении ЭДС источника берется со знаком плюс, если движение идет от отрицательного полюса к положительному плюсу источника, со знаком минус, если движение идет от положительного полюса к отрицательному

При составлении уравнений необходимо поступать так: 1. 2. 3. 4. Обозначить стрелками направления токов произвольно. Если в результате вычислений окажется, что какой-то ток положителен, то его направление было выбрано верно, если отрицателен – то его направление противоположно выбранному. Выбрать произвольный замкнутый контур и направление его обхода. Если предположительное направление тока совпадает с направлением обхода, то слагаемое IR следует брать со знаком плюс, если направления противоположны – со знаком минус. Если какая-то ЭДС повышает потенциал в направлении обхода (от минуса к плюсу источника), то ее надо брать со знаком плюс, а если понижает – со знаком минус.

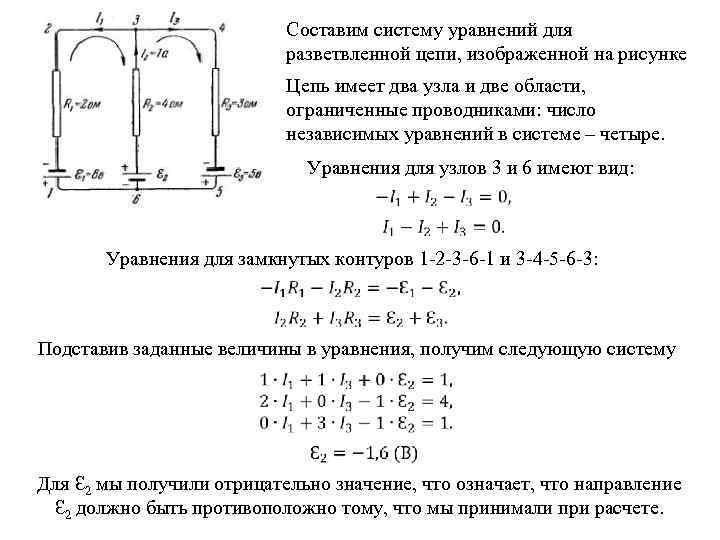Составим систему уравнений для разветвленной цепи, изображенной на рисунке Цепь имеет два узла и две области, ограниченные проводниками: число независимых уравнений в системе – четыре. Уравнения для узлов 3 и 6 имеют вид: Уравнения для замкнутых контуров 1 -2 -3 -6 -1 и 3 -4 -5 -6 -3: Подставив заданные величины в уравнения, получим следующую систему Для Ԑ 2 мы получили отрицательно значение, что означает, что направление Ԑ 2 должно быть противоположно тому, что мы принимали при расчете.

При прохождении по проводнику тока проводник нагревается. Рассмотрим однородный проводник, к которому приложено напряжение U. За время dt через проводник проходит заряд dq=idt. При этом силы поля совершают работу d. A=Udq=Uidt. Заменяя U в соответствии с законом Ома и интегрируя по времени, получим Закон Джоуля-Ленца

Коэффициент полезного действия источника тока Ток в цепи Напряжение на нагрузке Работа, совершаемая над переносимым вдоль цепи зарядом dq Полная мощность P, выделяемая во всей цепи

В нагрузке выделится только часть этой мощности (полезная мощность) Мощность Pн, выделяемая на нагрузке Коэффициент полезного действия источника тока КПД будет тем больше, чем больше сопротивление нагрузки R по сравнению с сопротивлением источника r.

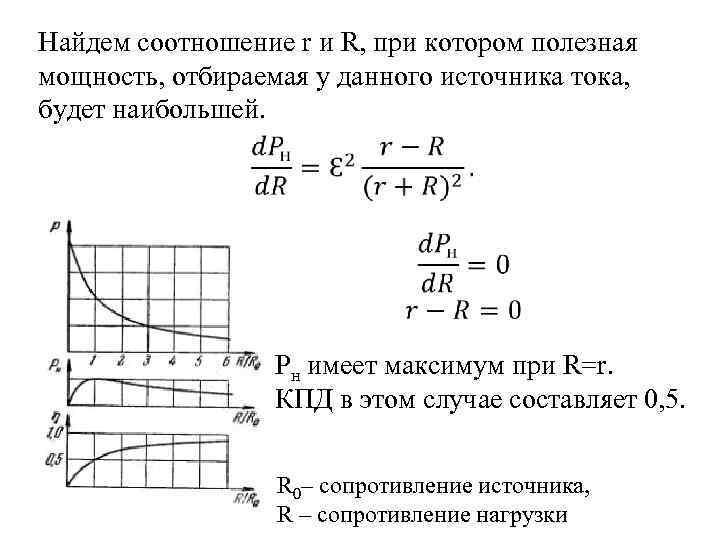Найдем соотношение r и R, при котором полезная мощность, отбираемая у данного источника тока, будет наибольшей. Pн имеет максимум при R=r. КПД в этом случае составляет 0, 5. R 0– сопротивление источника, R – сопротивление нагрузки

Взаимодействие токов Два тонких прямолинейных параллельных проводника, по которым текут токи (такие токи называются прямыми токами), притягивают друга, если токи в них имеют одинаковое направление, и отталкиваются, если направления токов противоположны. где μ 0 – магнитная постоянная, равная μ 0=4π· 10 -7 Г/м. Сила взаимодействия, приходящаяся на единицу длины каждого из параллельных проводников, пропорциональна силам токов в них I 1 и I 2 и обратно пропорциональна расстоянию b между ними

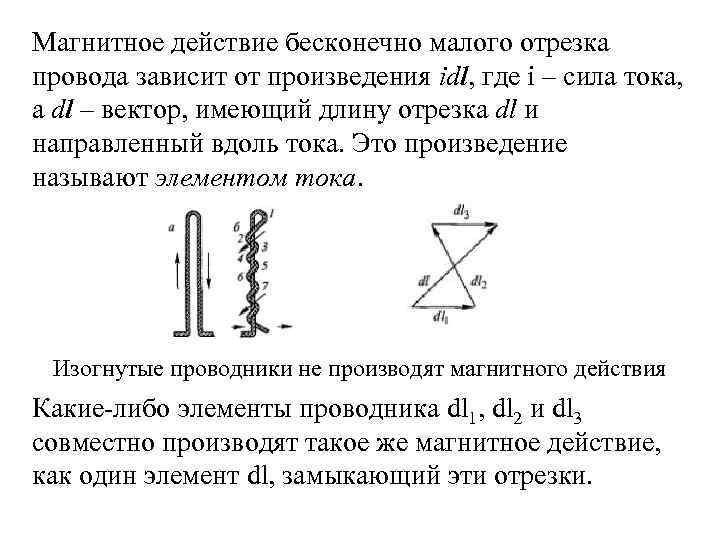Магнитное действие бесконечно малого отрезка провода зависит от произведения idl, где i – сила тока, а dl – вектор, имеющий длину отрезка dl и направленный вдоль тока. Это произведение называют элементом тока. Изогнутые проводники не производят магнитного действия Какие-либо элементы проводника dl 1, dl 2 и dl 3 совместно производят такое же магнитное действие, как один элемент dl, замыкающий эти отрезки.

Взаимодействие токов осуществляется через поле, называемое магнитным. Магнитное поле имеет направленный характер и должно характеризоваться векторной величиной. Основная силовая характеристика магнитного поля – магнитная индукция B. Магнитное поле порождается движущимися зарядами. Поле проявляется себя в том, что на движущиеся в нем заряды действуют силы. Магнитное поле в отличие от электрического не оказывает действия на покоящийся заряд.

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: поле B, порождаемое несколькими движущимися зарядами (токами), равно векторной сумме полей Bi, порождаемых каждым зарядом (током) в отдельности

На заряд, движущийся в магнитном поле, действует сила где α – угол между векторами v и B. Магнитная сила направлена перпендикулярно плоскости, в которой лежат вектора v и B. Если заряд q>0, то направление силы совпадает с направлением вектора [v, B], если q<0, то направление силы противоположно направлению вектора [v, B].

Магнитная сила всегда направлена перпендикулярно скорости движения заряда, поэтому магнитная сила работы над зарядом не совершает. Это означает, что в постоянном магнитном поле энергия движущейся частицы остается постоянной, как бы частица не двигалась. Если имеются одновременно магнитное и электрическое поля, то на движущуюся заряженную частицу действует сила, равная Эту силу называют силой Лоренца.

Поле движущегося заряда Рассмотрим поле, создаваемое в некоторой точке P движущимся со скоростью v зарядом q. Возмущения поля передаются от точки к точке пространства с конечной скоростью, поэтому индукция в момент времени t определяется не положением в тот же момент времени t, а положением заряда в некоторый более ранний момент времени t-τ. Если скорость заряда v «c, то время запаздывания будет пренебрежимо мало, и в этом случае можно будет считать, что значение вектора B в момент времени t будет определяться положением заряда в тот же момент времени t. или через единичный вектор n, направленный вдоль радиус вектора

Электрическое поле точечного заряда, двигающегося с нерелятивистской скоростью, определятся так же, как и поле неподвижного заряда где c – электродинамическая постоянная, она равна скорости света в вакууме. Начало радиус-вектора r связано с зарядом и движется вместе с ним со скоростью v. Вектор B направлен перпендикулярно плоскости, в которой расположены вектора v и r.

Сравним силы магнитного и электрического взаимодействия движущихся зарядов. Пусть два точеных достаточно массивных заряда движутся параллельно другу с одинаковой нерелятивистской скоростью v. Найдем отношение магнитной силы Fм и электрической сил Fэ, действующих со стороны заряда 1 на заряд 2. где v – скорость заряда 2, а B и E – индукция магнитного и напряженность электрического полей, создаваемых зарядом 1 в месте нахождения заряда 2.

Закон Ампера Магнитное поле B взывает появление механической силы, действующей на какой-либо элемент тока idl Полную величину силы, действующей на проводник конечных размеров можно найти, суммируя силы на отдельных его элементах. Для прямолинейного участка провода и постоянной магнитной индукции Направление силы перпендикулярно к l и B подчиняется правилу буравчика: при движении рукоятки буравчика от вектора l к вектору B поступательное движение происходит в направлении силы F.

Модуль силы Ампера вычисляется по формуле где α – угол между векторами dl и B. Сила взаимодействия, приходящаяся на единицу длины каждого из параллельных проводников На каждый элемент тока второго проводника I 2 dl будет действовать магнитное поле первого проводника, индукция которого равна B 1=(μ 0/4π)(2 I 1/b). На единицу длины второго проводника действует сила μ 0 – магнитная постоянная

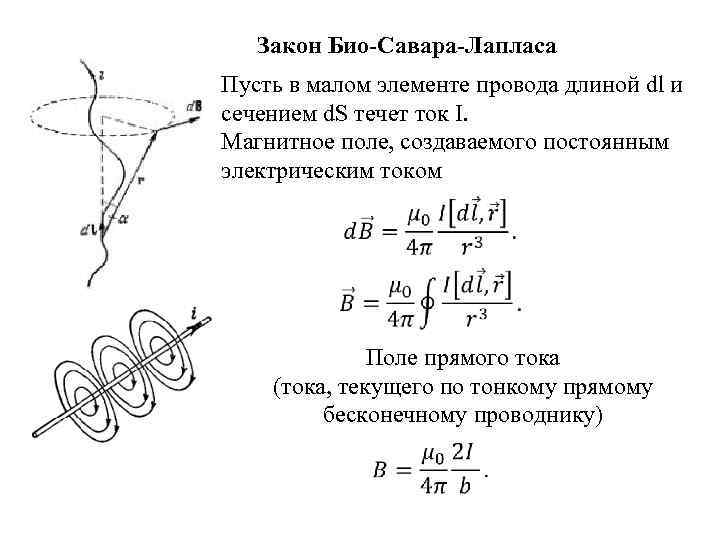Закон Био-Савара-Лапласа Пусть в малом элементе провода длиной dl и сечением d. S течет ток I. Магнитное поле, создаваемого постоянным электрическим током Поле прямого тока (тока, текущего по тонкому прямому бесконечному проводнику)

Силовые линии магнитного поля Магнитное поле B может быть представлено наглядно с помощью линий вектора B, которые проводят так, чтобы касательная к этим линиям в точке совпадала с направлением вектора B, а густота линий была пропорциональна модулю вектора в данном месте. Направление силовой линии в каждой точке может быть только единственным, поэтому магнитные линии поля не пересекаются, так же, как и силовые линии электрического поля.

Контур с током в магнитном поле Элементарный контур – это плоский контур очень малых размеров с током. Положительная нормаль к контуру связана с направлением тока в контуре правилом правого винта. Магнитный момент pm Сила, действующая на элементарный контур с током в неоднородном магнитном поле где pm – модуль магнитного момента, ∂B/∂n – производная вектора B по направлению нормали n.

Пусть элементарный контур с током, имеющий магнитный момент pm, расположен перпендикулярно оси симметрии неоднородного магнитного поля так, что вектор pm направлен вдоль вектора поля B (см. рис. ) Так как в направлении pm приращение вектора B будет отрицательным, то сила будет направлена влево, в сторону, где поле больше. Если направление тока сменить на противоположное, при этом pm будет противоположен вектору B, то сила будет направлена вправо – контур будет выталкиваться из поля. Момент сил, действующий на контур с током Когда pm↑↑B, то момент сил M=0, положение контура является устойчивым. Когда pm↑↓B, то момент сил также равен нулю, но это положение является неустойчивым.

Работа, совершаемая при перемещении тока в магнитном поле Рассмотрим контур со свободно перемещающимся за счет скользящих контактов проводом. Сила, действующая на подвижную перемычку, будет направлена вправо и равна Изменение потока магнитной индукции через контур

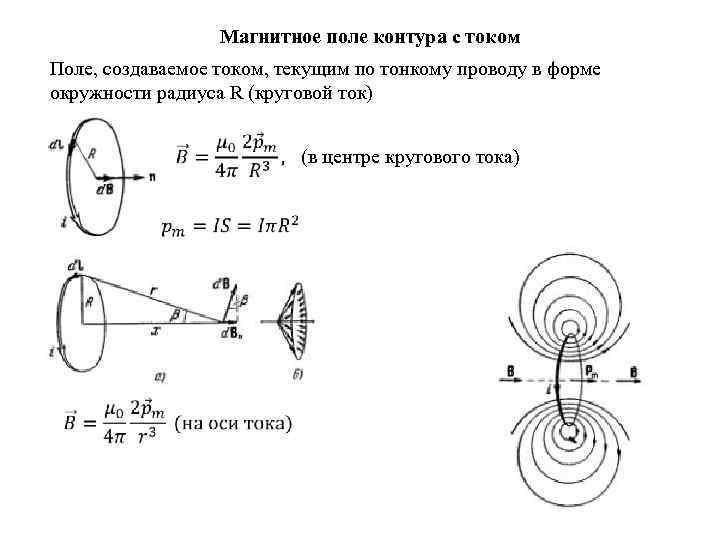Магнитное поле контура с током Поле, создаваемое током, текущим по тонкому проводу в форме окружности радиуса R (круговой ток) (в центре кругового тока)

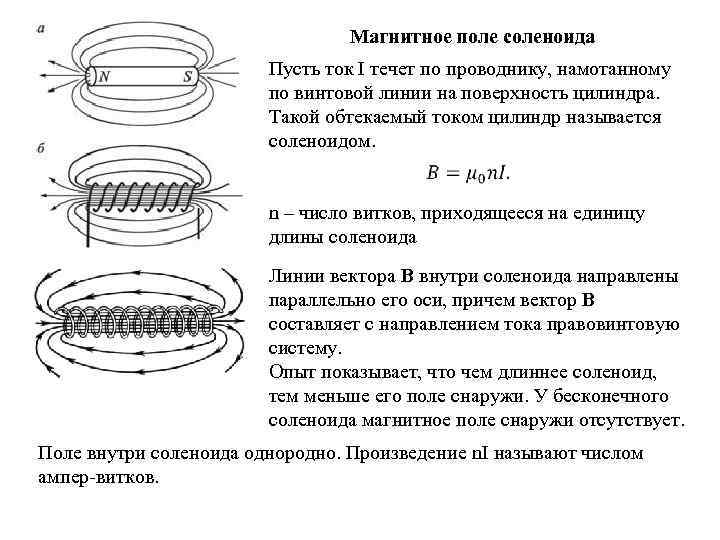Магнитное поле соленоида Пусть ток I течет по проводнику, намотанному по винтовой линии на поверхность цилиндра. Такой обтекаемый током цилиндр называется соленоидом. n – число витков, приходящееся на единицу длины соленоида Линии вектора B внутри соленоида направлены параллельно его оси, причем вектор B составляет с направлением тока правовинтовую систему. Опыт показывает, что чем длиннее соленоид, тем меньше его поле снаружи. У бесконечного соленоида магнитное поле снаружи отсутствует. Поле внутри соленоида однородно. Произведение n. I называют числом ампер-витков.

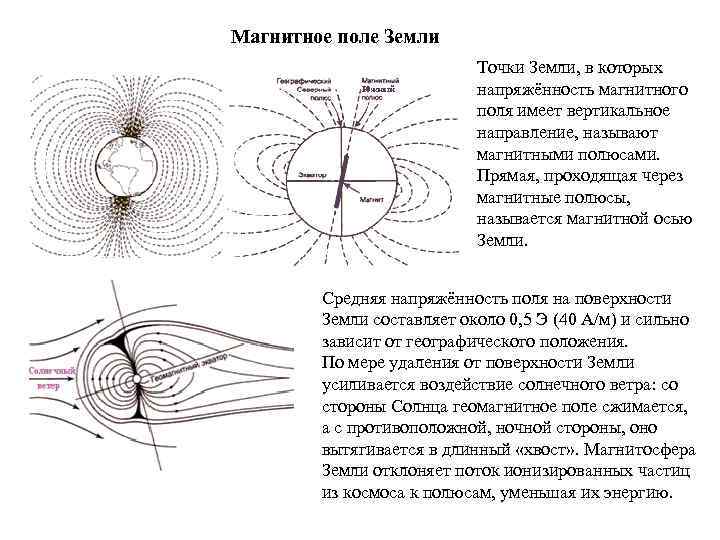Магнитное поле Земли Точки Земли, в которых напряжённость магнитного поля имеет вертикальное направление, называют магнитными полюсами. Прямая, проходящая через магнитные полюсы, называется магнитной осью Земли. Средняя напряжённость поля на поверхности Земли составляет около 0, 5 Э (40 А/м) и сильно зависит от географического положения. По мере удаления от поверхности Земли усиливается воздействие солнечного ветра: со стороны Солнца геомагнитное поле сжимается, а с противоположной, ночной стороны, оно вытягивается в длинный «хвост» . Магнитосфера Земли отклоняет поток ионизированных частиц из космоса к полюсам, уменьшая их энергию.

Единицей магнитной индукции является тесла (Тл) – численно равная индукции такого однородного магнитного поля, в котором на 1 метр длины прямого проводника, перпендикулярного вектору магнитной индукции, с током силой 1 А действует сила 1 Н.

Намагничивание вещества. Намагниченность Вектор намагниченности – магнитный момент единицы объема χ – магнитная восприимчивость Напряженность магнитного поля μ=1+χ – относительная магнитная проницаемость или просто магнитная проницаемость

Электрон, двигаясь по круговой орбите, переносит через любую площадку, расположенную на его траектории, заряд eν (ν – число оборотов в секунду). Т. е. движение электрона образует круговой ток силы I=eν, направленный в сторону, противоположную движению электрона, т. к. заряд электрона отрицателен. Магнитный момент электрона (орбитальный магнитный момент электрона) где r – радиус орбиты электрона, v=2πνr – скорость движения электрона Движущийся по орбите электрон обладает орбитальным механическим моментом, который образует с направлением движения электрона правовинтовую системы и, соответственно, направлен противоположно вектору pm

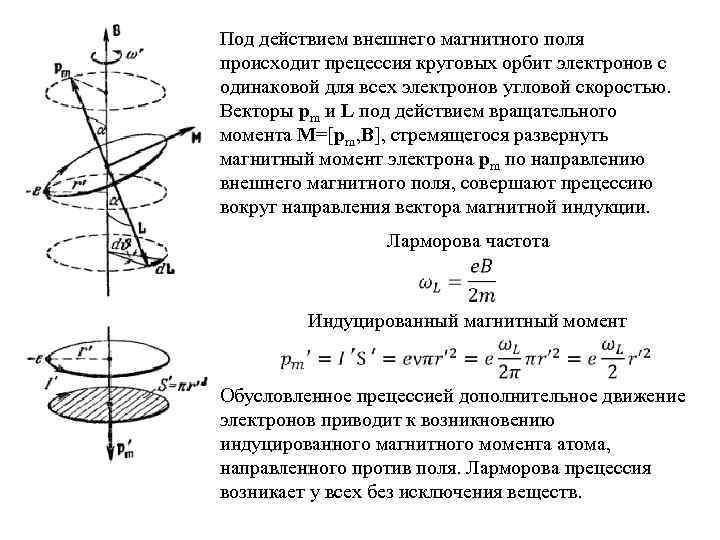Под действием внешнего магнитного поля происходит прецессия круговых орбит электронов с одинаковой для всех электронов угловой скоростью. Векторы pm и L под действием вращательного момента М=[pm, B], стремящегося развернуть магнитный момент электрона pm по направлению внешнего магнитного поля, совершают прецессию вокруг направления вектора магнитной индукции. Ларморова частота Индуцированный магнитный момент Обусловленное прецессией дополнительное движение электронов приводит к возникновению индуцированного магнитного момента атома, направленного против поля. Ларморова прецессия возникает у всех без исключения веществ.

Виды магнетиков 1. 2. 3. Диамагнетики (μ<1) Парамагнетики (μ>1) Ферромагнетики (μ» 1) 1. Диамагнетики (μ<1) У диамагнетиков J↑↓H, χ<0. Диамагнетики не обладают в отсутствии внешнего поля собственным магнитным моментом (векторная сумма всех орбитальных и спиновых моментов электронов атома равна нулю). Под действием внешнего поля у диамагнетиков возникает индуцированный магнитный момент, направленный против поля, обусловленный прецессией электронных орбит. Намагниченность диамагнетиков изменяется с напряженностью поля линейно.

3. Ферромагнетики (μ» 1) Ферромагнетики способны обладать намагничиванием даже в отсутствие внешнего поля. Они являются сильномагнитными веществами. Намагниченность ферромагнетиков изменяется с напряженностью поля нелинейно. Магнитные свойства ферромагнетиков обуславливаются очень сильной ориентацией собственных магнитных моментов электронов (спинов), но не магнитных моментов атома в целом. Основная кривая намагничения при J=Jнас. Br– остаточная индукция, Jr –остаточная намагниченность Нс – коэрцитивная сила

– основная кривая намагничения При неограниченном возрастании H магнитная проницаемость μ→ 1

Явление электромагнитной индукции Закон электромагнитной индукции Знак минус означает, что направление ЭДС и изменение потока магнитной индукции имеют противоположные направления ЭДС индукции в контуре, состоящем из N одинаковых витков Правило Ленца позволяет найти направление индукционного тока: индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей.

Электромагнитная самоиндукция Магнитный поток Ψ через контур пропорционален силе тока I где L –индуктивность ЭДС самоиндукции Энергия магнитного поля Объемная плотность энергии

Уравнения Максвелла представляют собой следующие законы: 1. Закон Фарадея (электромагнитной индукции). 2. Закон Ампера с током смещения Максвелла. 3. Закон Кулона (как его следствие - теорема Гаусса для электростатического поля). 4. Магнитных зарядов в природе не существует.

Движение заряженных частиц в электрических и магнитных полях В однородном магнитном поле, v⊥B Частица движется равномерно по окружности с радиусом В однородном магнитном поле, α=(v^B) Движение частицы можно представить как наложение двух движений: 1). Перемещения вдоль направления B с постоянной скоростью v||. 2). Равномерного вращения в плоскости, перпендикулярной к вектору B.

Движение частицы в электрическом поле Траектория движения частицы будет представлять параболу Движение частицы можно представить в виде суммы двух движений: 1). вдоль оси х с постоянной скоростью v 0 2). вдоль оси y под действием силы электрического поля – равноускоренно Угол отклонения α