Скачать презентацию ЭЛЕКТРИЧЕСКИЙ ТОК Направленное движение зарядов называется электрическим
ЭЛЕКТРИЧЕСКИЙ ток1.pptx
- Количество слайдов: 70
ЭЛЕКТРИЧЕСКИЙ ТОК
Направленное движение зарядов называется электрическим током. За направление тока принимается направление движения + зарядов. Свойство тел пропускать электрический ток называется проводимостью. По этому признаку все тела можно условно разделить на проводники и изоляторы. Такого рода разделение является достаточно условным –так существует целый класс веществ – полупроводники, находящийся между проводниками и изоляторами , проводимость которых может изменяться в зависимости от различного рода внешних воздействий. Помимо того диэлектрики, которые являются изоляторами, в определенных условиях становятся проводниками.
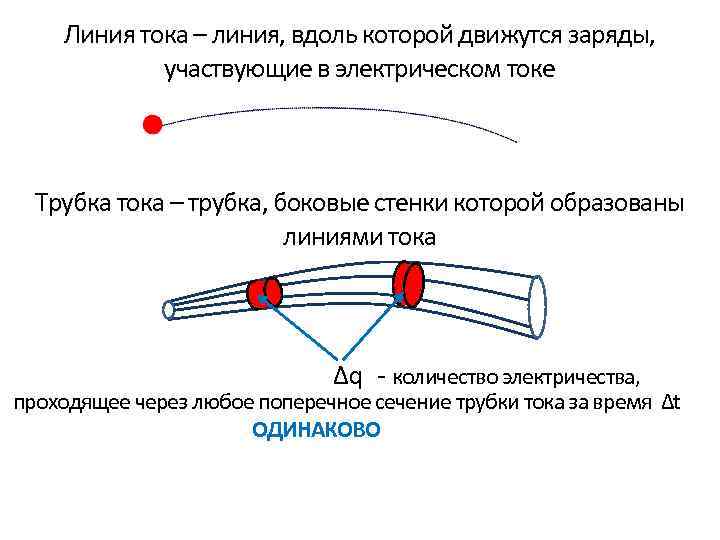Линия тока – линия, вдоль которой движутся заряды, участвующие в электрическом токе Трубка тока – трубка, боковые стенки которой образованы линиями тока Δq - количество электричества, проходящее через любое поперечное сечение трубки тока за время Δt ОДИНАКОВО
При приложении напряжения к проводнику возникает электрический ток Сила тока I – физическая величина, характеризующая скорость потока заряженных частиц, равная количеству электричества Δq, проходящему через поперечное сечение проводника за время Δt, отнесенному к этому интервалу времени: или в дифференциальной форме:
Плотность тока j – векторная величина, связывающая силу тока с поперечным сечением проводника. Плотность тока равна количеству электричества Δq, проходящему через поперечное сечение проводника Δ S˔за время Δt, отнесенное к этой площадке и этому интервалу времени: Связь силы и плотности тока
Уравнение неразрывности Рассмотрим связь между силой и плотностью тока для замкнутой поверхности интегрирования S: но Знак – означает убывание Поток вектора плотности тока через замкнутую поверхность равен скорости убывания заряда из объема, ограниченного этой поверхностью
Связь плотности тока со скоростью упорядоченного движения носителей заряда Скорость движения носителей заряда можно представить в виде: V = Vy +Vтепл. где Vy - скорость упорядоченного движения, Vтепл. - скорость теплового хаотического движения. Среднее значение скорости теплового хаотического движения равно нулю, поэтому носители заряда, участвующие только в в тепловом движении не создают электрический ток.
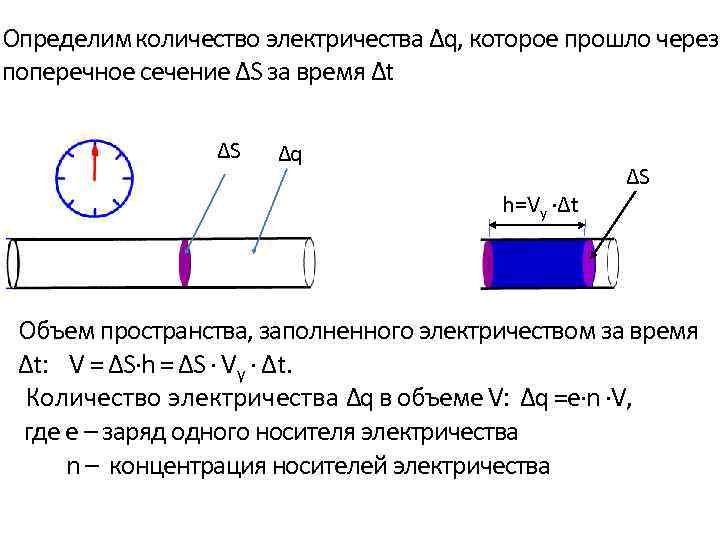Определим количество электричества Δq, которое прошло через поперечное сечение ΔS за время Δt ΔS Δq h=Vy ∙Δt ΔS Объем пространства, заполненного электричеством за время Δt: V = ΔS∙h = ΔS ∙ Vy ∙ Δt. Количество электричества Δq в объеме V: Δq =е∙n ∙V, где е – заряд одного носителя электричества n – концентрация носителей электричества
Плотность тока С учетом того, что в токе могут участвовать заряды обоих знаков:
Источники тока
Источник тока - это устройство, в котором происходит преобразование какого-либо вида энергии в электрическую энергию, поскольку только силы электростатического взаимодействия не в состоянии обеспечить непрерывное поддержание электрического тока. В любом источнике тока совершается работа по разделению положительно и отрицательно заряженных частиц, которые накапливаются на полюсах источника.
Историческое введение
Лейденская банка - первый источник тока. Лейденская банка (Л. Б. ) - стеклянный сосуд, стенки которого снаружи и изнутри оклеены свинцовой фольгой. Л. Б. была изобретена в середине XVIII в. в Голландии, в Лейденском университете, учеными под руководством Питера ван Мушенбрука. Они использовали электрическую машину для зарядки Л. Б. При соединении обкладок Л. Б. толстой проволокой в месте замыкания проскакивала сильная искра. Так стало возможным получить кратковременный электрический ток. Затем банку надо было снова заряжать.
Первый химический источник тока был изобретён итальянским учёным Алессандро Вольта в 1800 году. Это был элемент Вольта — сосуд с солёной водой с опущенными в него цинковой и медной пластинками, соединенными проволокой. Затем учёный собрал батарею из этих элементов, которая впоследствии была названа Вольтовым столбом. Это изобретение впоследствии использовали другие учёные в своих исследованиях - в 1802 году русский академик В. В. Петров сконструировал Вольтов столб из 2100 элементов для получения электрической дуги. - в 1836 году английский химик Джон Дэниель усовершенствовал элемент Вольта, поместив цинковый и медный электроды в раствор серной кислоты.
В 1859 году французский физик Гастон Плантэ изобрёл свинцово-кислотный аккумулятор. Этот тип элемента и по сей день используется в автомобильных аккумуляторах.
В 1865 году французский химик Ж. Лекланше предложил свой гальванический элемент (элемент Лекланше), состоявший из цинкового стаканчика, заполненного водным раствором хлористого аммония или другой хлористой соли, в который был помещён агломерат из оксида марганца Mn. O 2 с угольным токоотводом. Модификация этой конструкции используется до сих пор в солевых батарейках для различных бытовых устройств — на каждые 10 миллиардов выпускаемых в мире сухих батарей на долю элементов Лекланше приходится 9 миллиардов!
Классификация источников тока по принципу действия
Механические источники тока Электрофорная машина Диски машины приводятся во вращение в противоположных направлениях. В результате трения щеток о диски на кондукторах машины (лейденские банки) накапливаются заряды противоположного знака. При этом разность потенциалов на разрядниках достигает нескольких сотен тысяч вольт. В настоящее время электрофорная машина используется как демонстрационный прибор по теме «электричество» .
Одной из разновидностью электростатических генераторов является генератор Ван-де-Граафа, который до настоящего времени используется для ускорения заряженных частиц в ядерной физике Он состоит из большого полого проводника 1 в виде шара, укрепленного на изолирующей колонне 2. Внутри колонны проходит движущаяся бесконечная лента 3 из прорезиненной ткани, которая заряжается при помощи острия 4. Заряды, стекающие с острия 4 на ленту, переносятся на острие 5 и далее на внутреннюю поверхность полого шара 1. Этот заряд затем полностью переходят на внешнюю поверхность шара. С помощью генератора Ван-де-Граафа удается получить напряжения до нескольких десятков миллионов вольт. Эти генераторы имеют внушительные размеры – их высота достигает 10— 15 м, а диаметр шара несколько метров
Электростатические генераторы могли вырабатывать высокое напряжение, но имели маленький ток. Они имели низкую мощность и практически не использовались для выработки электроэнергии. Более эффективными оказались источники, использующие связь между электричеством и магнетизмом.
Принцип действия электромеханических генераторов основан на явлении электромагнитной индукции: переменный магнитный поток, пронизывающий проводящий контур, вызывает появление ЭДС индукции и соответственно электрического тока в этом контуре S N При этом совершенно неважно вращается ли контур в магнитном поле или неподвижный контур находится в изменяющемся магнитном поле
Динамо-машины и генераторы Генераторы переменного и постоянного тока, работа которых основана на явлении электромагнитной индукции, в настоящее время широко используются при промышленном производстве электроэнергии. При этом в качестве источника механической энергии могут выступать: кинетическая энергия воды (гидрогенератор), ветра (ветрогенератор), пара (парогенератор) Особо следует выделить магнитогидродинамический генератор (МГД), который напрямую вырабатывает электроэнергию из энергии движущейся через магнитное поле плазмы или другой подобной проводящей среды без использования вращающихся частей.
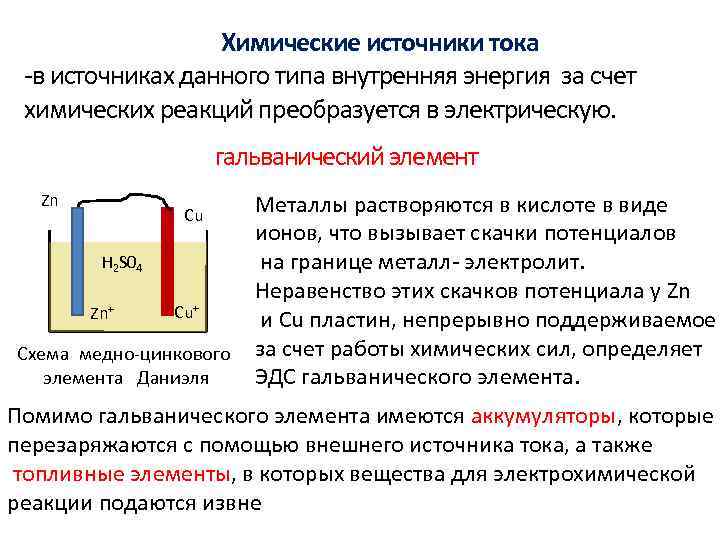Химические источники тока -в источниках данного типа внутренняя энергия за счет химических реакций преобразуется в электрическую. гальванический элемент Zn Cu H 2 S 04 Zn+ Cu+ Схема медно-цинкового элемента Даниэля Металлы растворяются в кислоте в виде ионов, что вызывает скачки потенциалов на границе металл- электролит. Неравенство этих скачков потенциала у Zn и Cu пластин, непрерывно поддерживаемое за счет работы химических сил, определяет ЭДС гальванического элемента. Помимо гальванического элемента имеются аккумуляторы, которые перезаряжаются с помощью внешнего источника тока, а также топливные элементы, в которых вещества для электрохимической реакции подаются извне
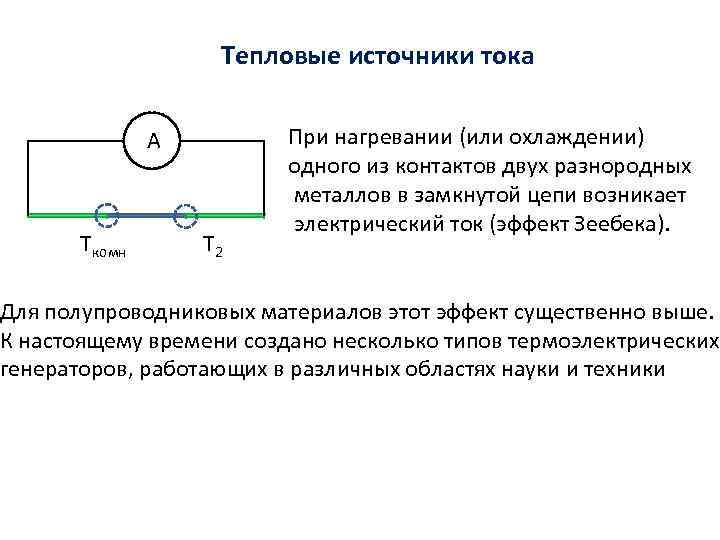Тепловые источники тока А Ткомн Т 2 При нагревании (или охлаждении) одного из контактов двух разнородных металлов в замкнутой цепи возникает электрический ток (эффект Зеебека). Для полупроводниковых материалов этот эффект существенно выше. К настоящему времени создано несколько типов термоэлектрических генераторов, работающих в различных областях науки и техники
Фотоэлектрические источники тока Фотоэлектрический генератор (Солнечная батарея) представляет собой совокупность фотоэлементов, преобразующих энергию свет солнечного излучения в электрическую. Солнечные батареи применяются главным образом в космической технике, а также для снабжения электроэнергией районов с большим числом солнечных дней в году
Электроизмерительные приборы Для изучения законов электрического тока необходимы данные о силе тока и напряжении на отдельных элементах электрической цепи
Первоосновой всех электроизмерительных приборов является гальванометр Гальвано метр – это высокочувствительный прибор для измерения малых электрических токов, напряжений и количества электричества. Существуют различные по принципу работу гальванометры - это магнитоэлектрические, электромагнитные, электродинамические, тепловые и ряд других. С помощью дополнительных проводников с различной проводимостью гальванометр может служить для измерения токов и напряжений в более широком диапазоне
В качестве примера рассмотрим принцип действия гальванометра магнитоэлектрического типа 5 4 S 3 1 1 – магниты; 2 - проволочная рамка, по которой пропускается измеряемый ток; 3 - пружина; 4 - стрелка; 5 - шкала; N 2
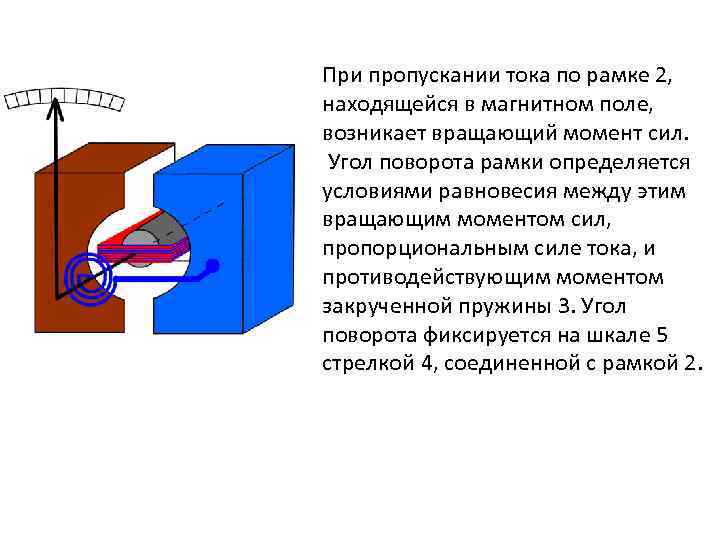При пропускании тока по рамке 2, находящейся в магнитном поле, возникает вращающий момент сил. Угол поворота рамки определяется условиями равновесия между этим вращающим моментом сил, пропорциональным силе тока, и противодействующим моментом закрученной пружины 3. Угол поворота фиксируется на шкале 5 стрелкой 4, соединенной с рамкой 2.
Для измерения силы электрического тока служит амперметр. Как было отмечено ранее, для измерения малых токов можно использовать гальванометр. Принцип действия амперметра, и гальванометра одинаковы. Амперметры предназначены для измерения бóльших токов. Гальванометр «легко превратить» в амперметр с помощью шунтирования, о чем речь пойдет ниже.
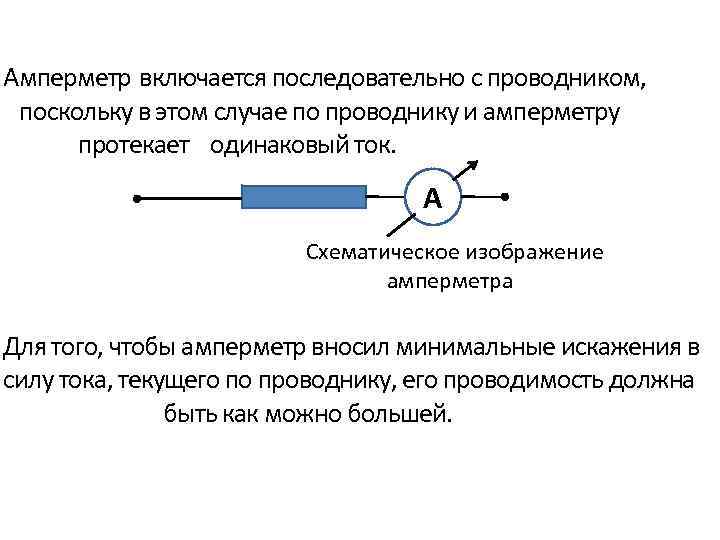Амперметр включается последовательно с проводником, поскольку в этом случае по проводнику и амперметру протекает одинаковый ток. А Схематическое изображение амперметра Для того, чтобы амперметр вносил минимальные искажения в силу тока, текущего по проводнику, его проводимость должна быть как можно большей.
Во многих случаях возникает необходимость измерить ток, существенно больший, чем это предусмотрено конструкцией амперметра. Тогда производится шунтирование амперметра, заключающееся в присоединении параллельно амперметру проводника, по которому проходит основная часть тока: А А шунт
Для измерения напряжения в цепи электрического тока служит вольтметр В отличие от амперметра вольтметр присоединяется параллельно проводнику V Схематическое изображение вольтметра Для того, чтобы вольтметр минимально искажал величину напряжения на проводнике, необходимо чтобы его проводимость была как можно меньшей
Гальванометр или амперметр можно превратить в вольтметр добавляется последовательно проводник, имеющий малую проводимость доп. проводник ограничивает ток, текущий по прибору, измеряющему напряжение Когда возникает необходимость измерить напряжение, существенно большее, чем это предусмотрено конструкцией вольтметра, то к уже имеющемуся дополнительному проводнику добавляется еще другой
ЗАКОН ОМА
Приложим напряжение U к концам проводника и определим зависимость силы тока I, текущего по проводнику, от величины напряжения
Изменяя ступенчатым образом напряжение, подаваемое на проводник, определим зависимость между U и I I 4 3 2 1 U 1 2 3 4 График этой зависимости – прямая линия
Повторим эксперимент, но уже с другим проводником I 4 3 2 1 U 1 2 3 4 И в этом случае сохраняется пропорциональность между I и U
Сравним эти графики I 1 -ый проводник 2 -ой проводник 4 3 2 1 U 1 2 3 4 При одном и том же напряжении ток, текущий по 1 -ому проводнику больше, чем по 2 -ому. Вывод № 1: Первый проводник обладает большей проводимостью
Вывод № 2: Сила тока в проводнике независимо от его проводящих свойств пропорциональна напряжению где G – проводимость проводника Однако общеупотребительной является обратная величина – сопротивление проводника R: Сила тока в проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна его сопротивлению
Сопротивление проводника R – это физическая величина, характеризующая свойство проводника препятствовать протеканию по нему электрического тока. По величине сопротивление R равно отношению напряжения U, приложенного к проводнику к силе тока I, текущему по нему
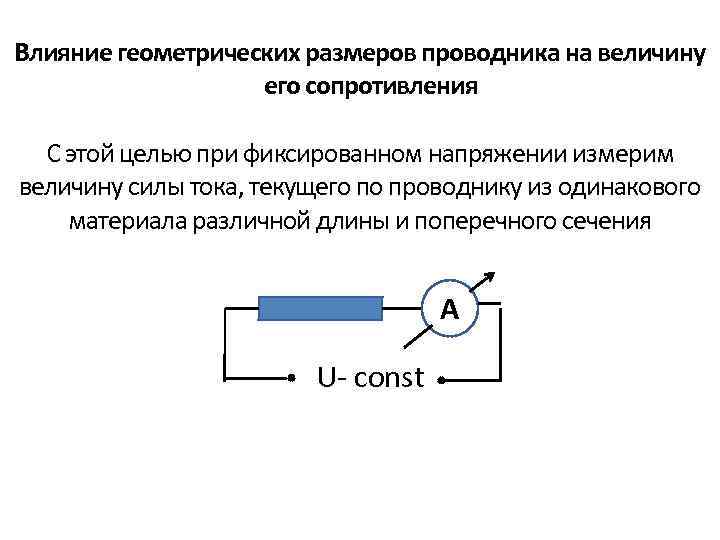Влияние геометрических размеров проводника на величину его сопротивления С этой целью при фиксированном напряжении измерим величину силы тока, текущего по проводнику из одинакового материала различной длины и поперечного сечения А U- const
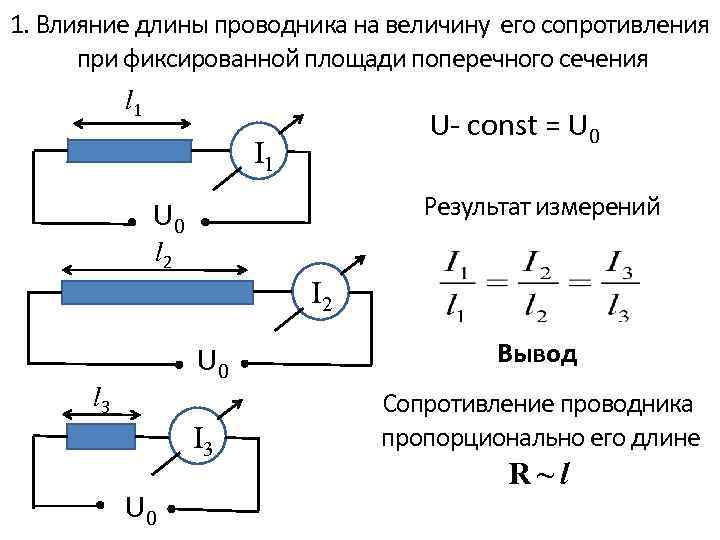1. Влияние длины проводника на величину его сопротивления при фиксированной площади поперечного сечения l 1 U- const = U 0 I 1 Результат измерений U 0 l 2 I 2 U 0 l 3 I 3 U 0 Вывод Сопротивление проводника пропорционально его длине R~l
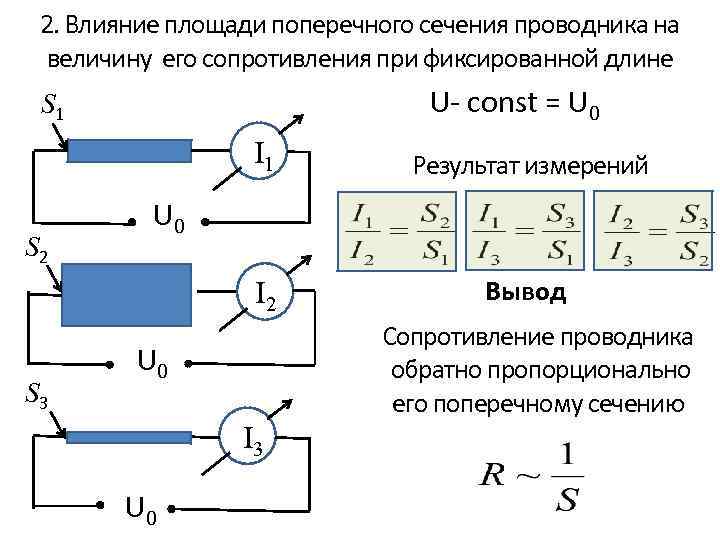2. Влияние площади поперечного сечения проводника на величину его сопротивления при фиксированной длине U- const = U 0 S 1 I 2 S 3 Результат измерений Вывод U 0 I 3 U 0 Сопротивление проводника обратно пропорционально его поперечному сечению
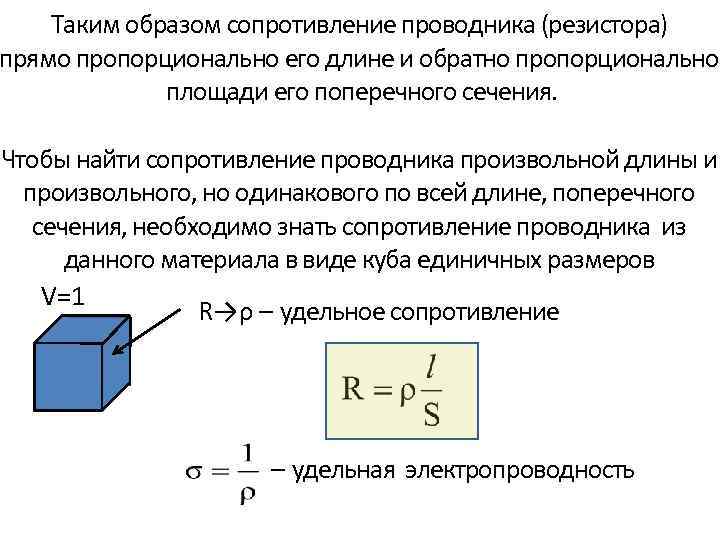Таким образом сопротивление проводника (резистора) прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения. Чтобы найти сопротивление проводника произвольной длины и произвольного, но одинакового по всей длине, поперечного сечения, необходимо знать сопротивление проводника из данного материала в виде куба единичных размеров V=1 R→ρ – удельное сопротивление – удельная электропроводность
Соединение проводников
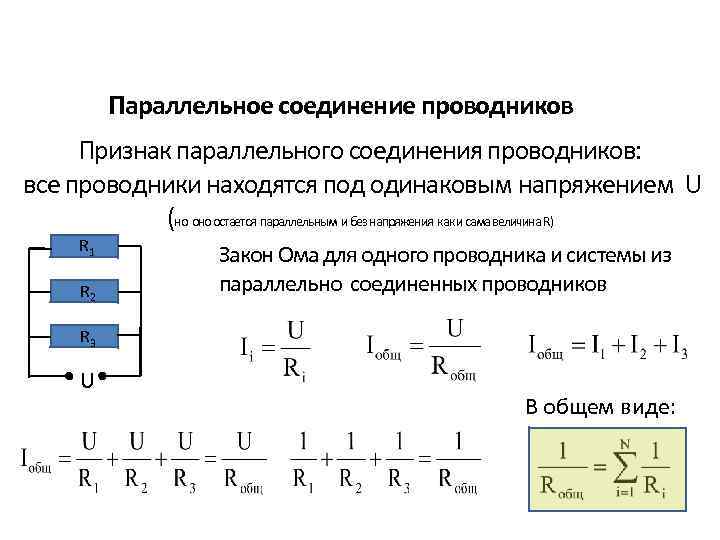Параллельное соединение проводников Признак параллельного соединения проводников: все проводники находятся под одинаковым напряжением U (но остается параллельным и без напряжения как и сама величина R) R 1 R 2 Закон Ома для одного проводника и системы из параллельно соединенных проводников R 3 U В общем виде:
Последовательное соединение проводников Признак последовательного соединения проводников: по всем проводникам проходит одинаковый ток I (но остается п-тельным и без напряжения как и сама величина R) R 1 R 2 U R 3 Закон Ома для одного проводника и системы из последовательно соединенных проводников В общем виде:
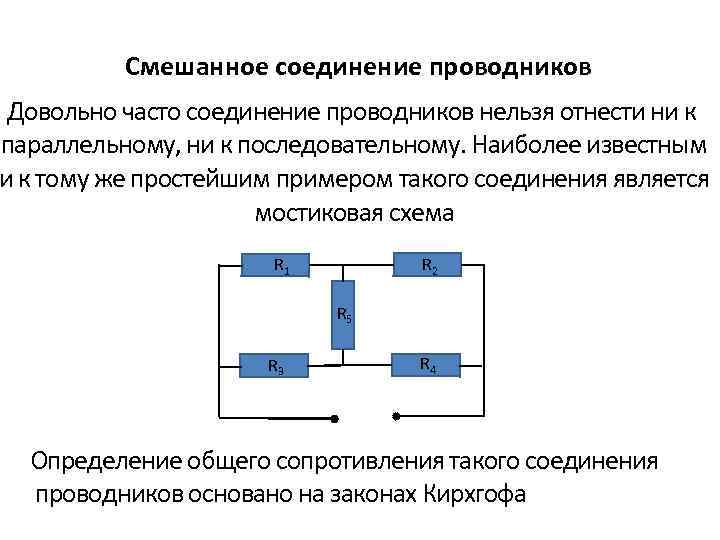Смешанное соединение проводников Довольно часто соединение проводников нельзя отнести ни к параллельному, ни к последовательному. Наиболее известным и к тому же простейшим примером такого соединения является мостиковая схема R 2 R 1 R 5 R 3 R 4 Определение общего сопротивления такого соединения проводников основано на законах Кирхгофа
Первый закон Кирхгофа I 3 I 1 I 2 I 4 I 1 + I 2 =I 3 + I 4 или I 1 + I 2 -I 3 - I 4= 0 Сумма токов, входящих в узел, равна сумме токов, исходящих из него
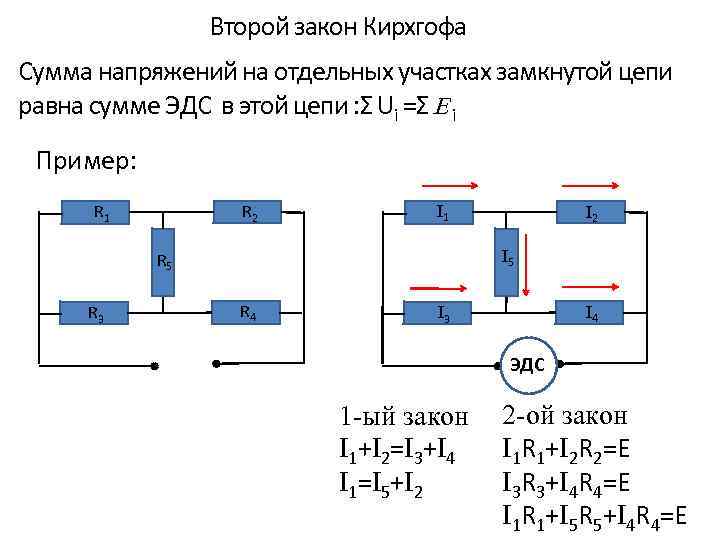Второй закон Кирхгофа Сумма напряжений на отдельных участках замкнутой цепи равна сумме ЭДС в этой цепи : Ʃ Ui =Ʃ E i Пример: R 2 R 1 I 5 R 3 I 2 R 4 I 3 ЭДС 1 -ый закон I 1+I 2=I 3+I 4 I 1=I 5+I 2 2 -ой закон I 1 R 1+I 2 R 2=E I 3 R 3+I 4 R 4=E I 1 R 1+I 5 R 5+I 4 R 4=E
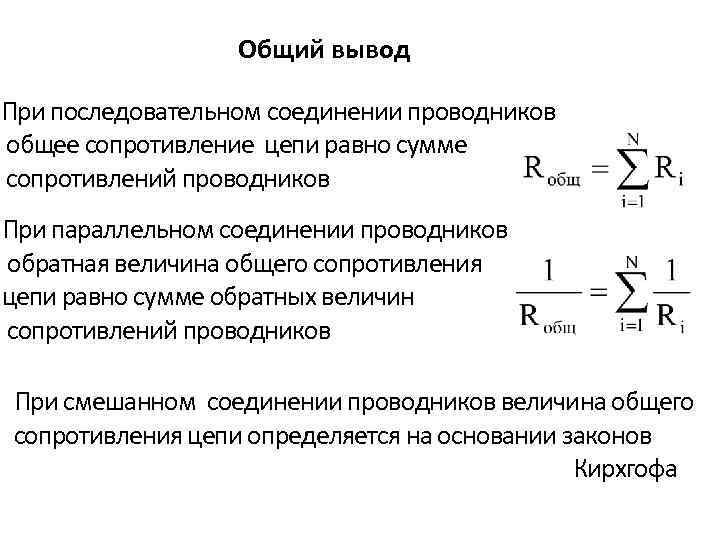Общий вывод При последовательном соединении проводников общее сопротивление цепи равно сумме сопротивлений проводников При параллельном соединении проводников обратная величина общего сопротивления цепи равно сумме обратных величин сопротивлений проводников При смешанном соединении проводников величина общего сопротивления цепи определяется на основании законов Кирхгофа
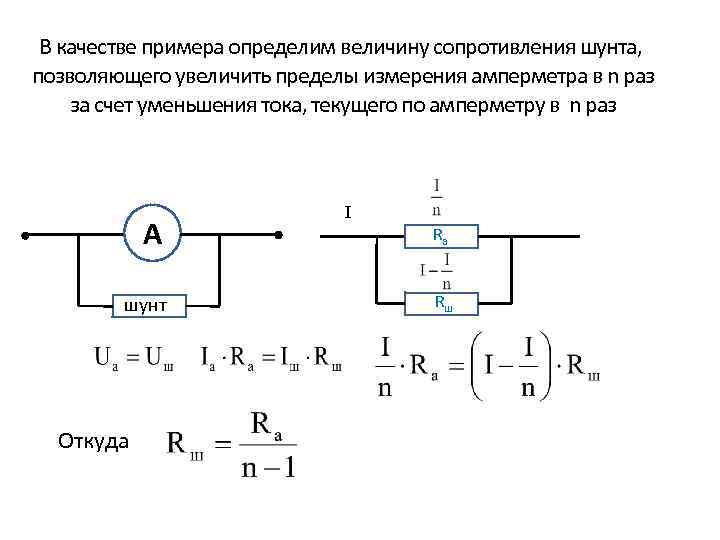В качестве примера определим величину сопротивления шунта, позволяющего увеличить пределы измерения амперметра в n раз за счет уменьшения тока, текущего по амперметру в n раз А шунт Откуда I Ra Rш
Закон Ома в дифференциальной форме Выделим в проводнике бесконечно малый объем в виде цилиндра, ось которого совпадает в направлением линии тока Линия тока Закон Ома в интегральной форме: S где dl и Подставим выражения (2 -5) в (1) : J = σ∙E
Закон Ома для цепи, содержащей ЭДС
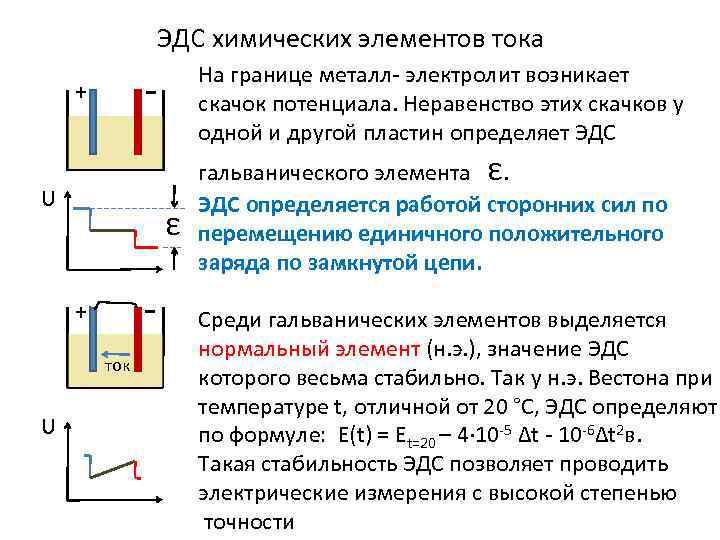ЭДС химических элементов тока - + U ε - + ток U На границе металл- электролит возникает скачок потенциала. Неравенство этих скачков у одной и другой пластин определяет ЭДС гальванического элемента ε. ЭДС определяется работой сторонних сил по перемещению единичного положительного заряда по замкнутой цепи. Среди гальванических элементов выделяется нормальный элемент (н. э. ), значение ЭДС которого весьма стабильно. Так y н. э. Вестона при температуре t, отличной от 20 °С, ЭДС определяют по формуле: E(t) = Et=20 – 4∙ 10 -5 Δt - 10 -6Δt 2 в. Такая стабильность ЭДС позволяет проводить электрические измерения с высокой степенью точности
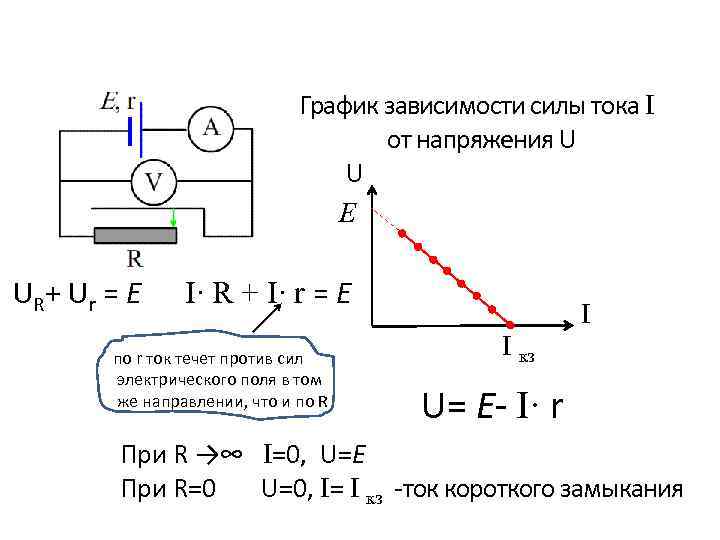График зависимости силы тока I от напряжения U U E UR+ Ur = E I∙ R + I∙ r = E по r ток течет против сил электрического поля в том же направлении, что и по R I I кз U= E- I∙ r При R →∞ I=0, U=E При R=0 U=0, I= I кз -ток короткого замыкания
Соединение гальванических элементов в батарею Гальванический элемент – это низковольтный, маломощный источник тока,
Контрольный Вопрос – как соединены r and R Каким должно быть R в качестве оптимальной нагрузки Зависимость от R мощностей
Закон Джоуля – Ленца в интегральной форме
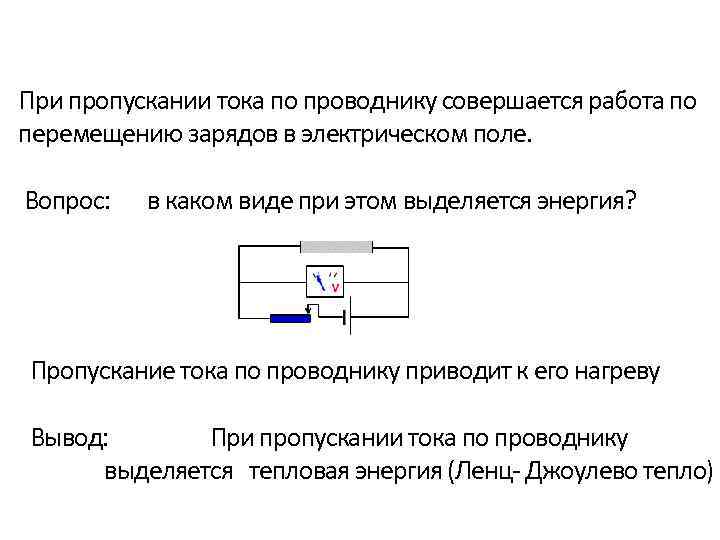При пропускании тока по проводнику совершается работа по перемещению зарядов в электрическом поле. Вопрос: в каком виде при этом выделяется энергия? Пропускание тока по проводнику приводит к его нагреву Вывод: При пропускании тока по проводнику выделяется тепловая энергия (Ленц- Джоулево тепло)
Работа по перемещению заряда q: A=q∙U, где U – разность потенциалов, проходимая зарядом. Если сила тока в проводнике I, то заряд, прошедший через поперечное сечение проводника равен: q= I∙t. С учетом закона Ома – U= I ∙R A=q∙U= I∙ t∙ I∙ R= I 2∙ R∙ t Откуда: Q= I 2∙ R∙ t Количество теплоты, выделяющееся в проводнике при прохождении электрического тока, пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока
Закон Джоуля – Ленца в дифференциальной форме
Выделим в проводнике бесконечно малый объем в виде цилиндра, ось которого совпадает в направлением линии тока и определим количество теплоты, Линия тока выделяющееся в этом объеме за время Δt, используя закон Джоуля-Ленца и S закон Ома в диф. Форме: dl ΔQ = I 2∙ R∙ Δt j =σ∙ E
w – удельная мощность – энергия, выделяемая в единицу времени в единице объема, вследствие прохождения электрического тока
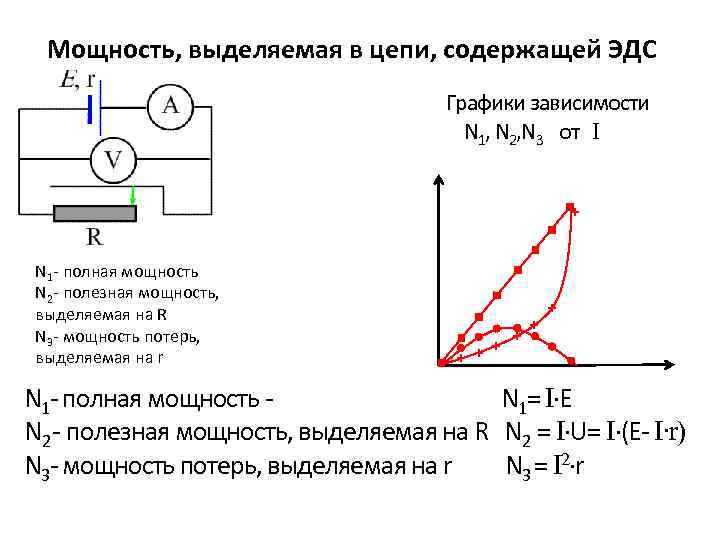Мощность, выделяемая в цепи, содержащей ЭДС Графики зависимости N 1, N 2, N 3 от I + N 1 - полная мощность N 2 - полезная мощность, выделяемая на R N 3 - мощность потерь, выделяемая на r + + + N 1 - полная мощность - N 1= I∙E N 2 - полезная мощность, выделяемая на R N 2 = I∙U= I∙(E- I∙r) N 3 - мощность потерь, выделяемая на r N 3 = I 2∙r
Механизмы проводимости
Два принципиальных вопроса: 1. Почему для множества проводников из разных материалов, находящихся в различном агрегатном состоянии (твердое тело, жидкость, газ) справедлив закон Ома? 2. Носитель тока в проводнике испытывает воздействие электрического поля и поэтому должен двигаться с ускорением: F=m∙a = q∙E, и, следовательно, скорость упорядоченного движения Vу должна линейно нарастать со временем приложении постоянного напряжения к проводнику Vу(t)= Vу0 +a∙ t и тогда j=e∙ n∙ Vу = f(t) Однако приложении постоянного напряжения к проводнику по нему протекает ПОСТОЯННЫЙ ток. Почему?
Феноменологическая теория проводимости Т. к. приложении постоянного напряжения к проводнику не происходит линейного нарастания тока со временем, то должен существовать механизм ограничивающий рост Vу. Будем считать, что в течении времени τ носитель заряда беспрепятственно движется под действием электрического поля. По истечению этого времени происходит некое взаимодействие в результате которого полностью теряется Vу. Этот процесс периодически повторяется.
Тогда Vу Vу max