ELECTROSTATICS 2 The work of the field forces

ELECTROSTATICS (2) The work of the field forces Circulation of the strength vector Electric potential Dielectrics and conductors Polarization of dielectrics Field in the dielectric The charges on the conductors Capacitance and capacitors Energy for the system of charged bodies

9. 9. The work of forces in the electrostatic field for the charge transportation Elementary work The field is created by charge +q. The Coulomb’s force moves in this field the probe charge qpr from the point a up to the point b. Elementary displacement After substitution of the Coulomb’s force we obtain the expression for the work of this force:

9. 10. Electric potential as the work for the unit probe charge transportation The work of electrostatic force work depends only on the initial and final distance (r 1, r 2) from the charge which creates the field. At the moving of the probe charge by external force against the electrostatic force the work done will has the opposite sign: DEFINITION: The potential in any point of electrostatic field is defined by the value of external force work needed for the transportation of the unit probe charge from infinity (r 2 = ) up to the point under consideration (r = r 1):

9. 11. Potential energy of the field for sole charge and for system of charges Potential energy of probe charge in the electrostatic field of sole charge For the pair of two electric charges the potential energy is When the field is created by several charges the potential from each charge is and potential energy for system of n charges is This is definition for energy of electrostatic field created by the system of charges.

9. 12. Mutual connection between the potential and gradient of the field strength At this simplest configuration of field the change of potential is maximal along the radial direction: Thus here Equipotential surfaces for the sole charge. In general case, when , the maximal change of potential along some direction l can be defined by the special vector function: is vector.

9. 13. Circulation of the strength vector in electrostatic field. Difference of potential The work on the probe charge transportation in the electrostatic field does not depend on the path form. Thus The circulation of the electrostatic field vector E along the closed contour is equal to zero: This is a specific property of the stationary electric fields which are not connected with moving charges. Difference of potential defines the work needed for transportation of the probe charge between two points of field: Difference of electric potential is measured in Volts (in the honour of Alessandro Volta [1745 – 1827], Italy, University of Pavia). 1 V = 1 Joule / 1 Coulomb

The University of Pavia, Italy (near Milan) – 650 years old. Founded at 1361. Alessandro Volta (1745 – 1827) was a professor of University of Pavia in 1778 – 1821. Inventor of the Voltaic Pile – the first battery A. Volta demonstrating the battery (1800). Alessandro Volta discovered the first practical method of generating electricity using chemical reactions.

Original voltaic pile of Alessandro Volta.

The monument of Alessandro Volta in the University of Pavia (rector in 1786 – 1787)

University of Pavia. City is disposed at the confluence of the rivers Ticino and Po. University, courtyard, Pavia (today).

Oldest University of Europe, the modern center of education for the northern Italy 25. 000 students in the University of Pavia (9 faculties, 16 colleges)

Pavia. Historical Hall of Alessandro Volta Physical Hall. Construction was completed in 1787. Restoration has been done in 1999.

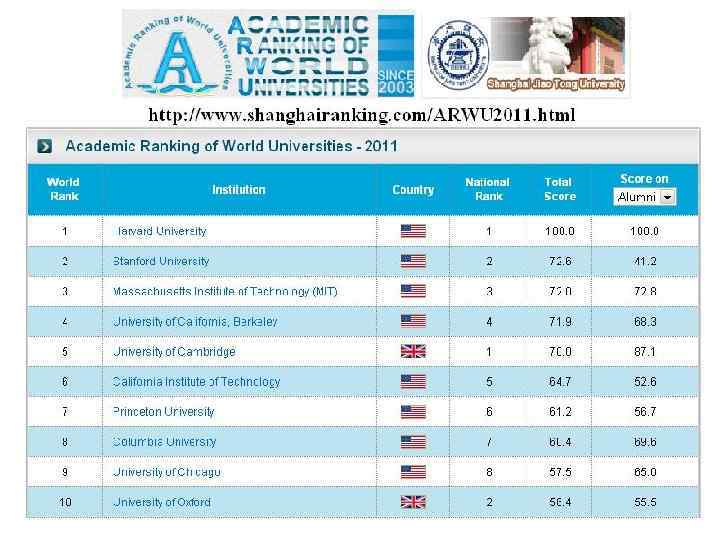
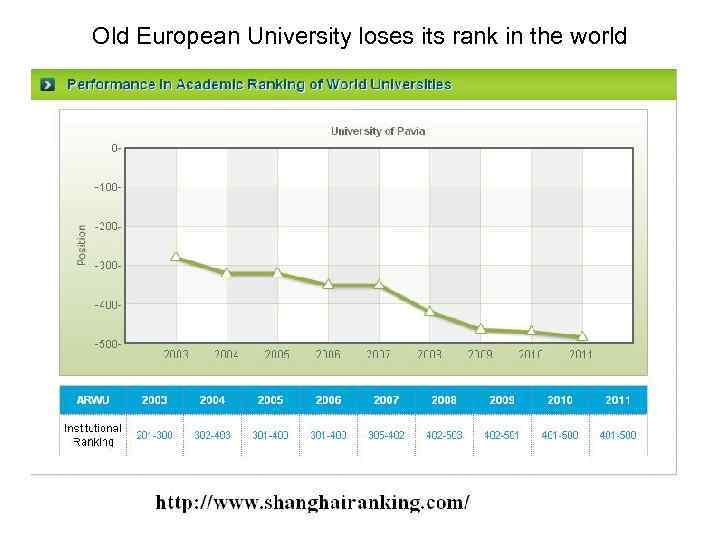Old European University loses its rank in the world

9. 14. Calculation of potential (the simplest situations) 1. Sphere of radius R charged on the surface with density σ. q = σ S = 4πR 2σ. For two points r 1 and r 2 out of sphere (r > R) due to E = Er we have E = - grad φ = - dφ/dr ; dφ = - E dr. Taking into account E = q / (4πεrε 0 r 2), difference of potential is Respectively Put r 1 = R, r 2 = , then potential at the surface of sphere is For any point of field with r > R the potential is or Inside of sphere q = 0, thus at r < R φ = 0 and E = 0.

9. 14. Calculation of potential (continuation) 2. Potential of electric field near the charged infinite plane. Electric field near the plane Integration between points M and N yields to

9. 14. Calculation of potential (continuation) 3. Difference of potential between two charged infinite plates (the surface density of charge is +σ and –σ respectively). Electrical field between the plates . Distance between the plates a = x 2 – x 1. Difference of potential (voltage) between the plates The system of two charged metal plates with opposite sign of charges is able to store the energy of electrostatic field and presents the simplest capacitor.

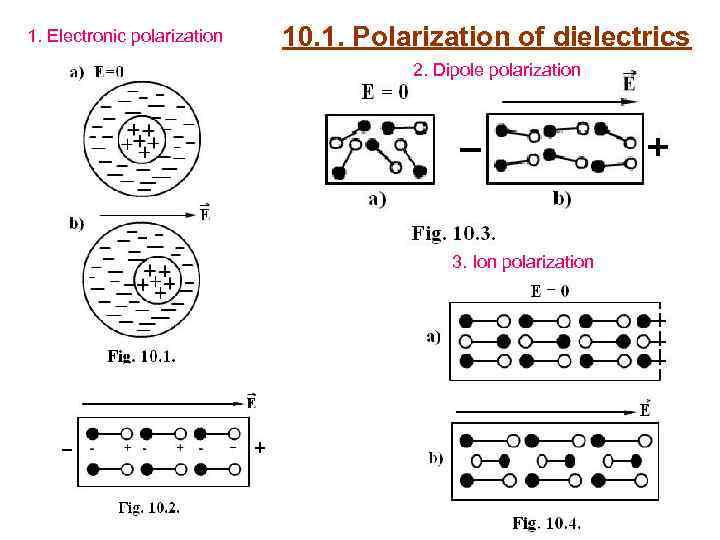1. Electronic polarization 10. 1. Polarization of dielectrics 2. Dipole polarization 3. Ion polarization

10. 2. Electric field in dielectrics Effect of polarization in dielectric can be measured by the sum of dipole moments of all molecules or atoms using the polarization vector P (calculated per unit of volume of dielectrics): is the elementary dipole moment of molecule or atom; n is the number of elementary dipoles in the volume ΔV. Direction of vector P is opposite to direction of applied external field E 0. The value of vector P is proportional to the strength of applied field: is a coefficient of dielectric susceptibility. Always > 0. Internal (induced) electric field in dielectric Resulting electric field inside of dielectrics In scalar form Relative dielectric constant of dielectric is . .

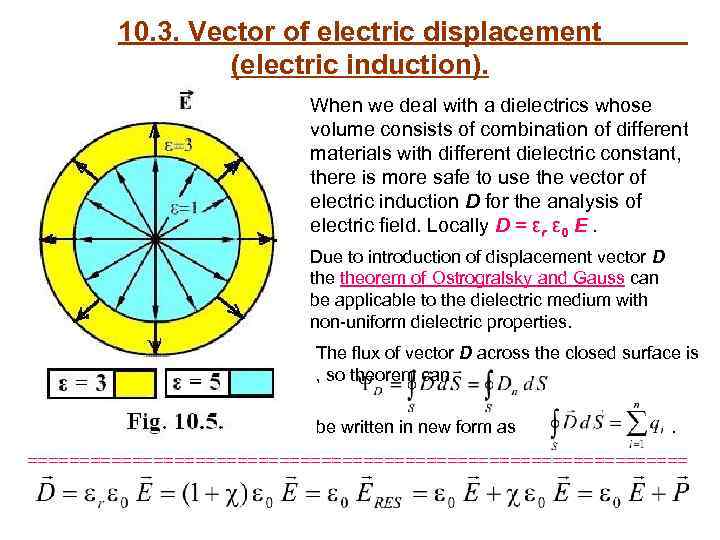10. 3. Vector of electric displacement (electric induction). When we deal with a dielectrics whose volume consists of combination of different materials with different dielectric constant, there is more safe to use the vector of electric induction D for the analysis of electric field. Locally D = εr ε 0 Ε. Due to introduction of displacement vector D theorem of Ostrogralsky and Gauss can be applicable to the dielectric medium with non-uniform dielectric properties. The flux of vector D across the closed surface is , so theorem can be written in new form as . ================================

11. 1. Electric charges at the conductor The main properties of conductor: 1) A presence of free charges (electrons) distributed inside the volume of conductor; 2) Mobility of free electrons; 3) Quasi-neutrality of conductor in the volume. Results: electrical field is equal to zero inside of conductor. Superfluous charges can exist only at the surface of conductor. Negatively charged conductor has the surplus of electrons at the near-surface layer. Positively charged conductor has a lack of electrons at the near-surface layer.

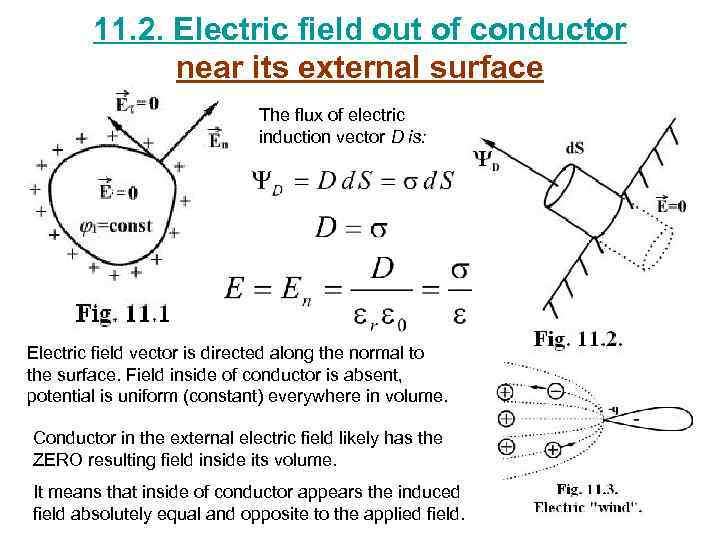11. 2. Electric field out of conductor near its external surface The flux of electric induction vector D is: Electric field vector is directed along the normal to the surface. Field inside of conductor is absent, potential is uniform (constant) everywhere in volume. Conductor in the external electric field likely has the ZERO resulting field inside its volume. It means that inside of conductor appears the induced field absolutely equal and opposite to the applied field.

11. 3. Electrical capacitance of conductor. Capacitor as element of electric circuit. Electric potential of sole charged body is proportional to its charge: . For a spherical charge: i. e. , . The coefficient of proportionality between the potential and charge is called as electrical capacity C. is a capacitance of sole sphere. The pair of metal sheets forms the electric device capacitor, strongly usable element of electrical circuits due to ability to store the energy of electrostatic field. The capacitance of the flat capacitor will be (here d is a distance between the plates of capacitor)

11. 4. Ohm’s law in differential form for element of conductor is a mean time between collision of electron with loss of momentum is a mean length of free run for electrons is a mean velocity of electrons drift under action of applied electric field The flow of charged particles trough time interval is (electric current) Current density

11. 4 a. Ohm’s law in differential form (continuation) The mean velocity of electron drift can be found on the base of classical theory. From the 2 nd Newton’s law. Current density In the vector form is the coefficient of electrical conductivity for conductor according to classical electron theory

11. 5. External forces for charges. Electromotive forces (EMF) in electric contour. For the support of current flow along the conductor there are two main conditions needed: 1) closed contour; 2) the presence of driving external force which provides a continuous charges division at some part of contour. The work of electrostatic forces at the passive part AB is Resulting force on the charges in active part of contour BA is The work of external forces against electrostatic ones is E = A 2 -1/q = A 2 -1= q. E. is the electromotive force. If the circuit will be opened (I = 0) it will be E = φ1 – φ 2 (voltage of opened source)

11. 6. Electrical voltage and Ohm’s law in the integral form On the passive part of contour we have only electrostatic field E. The potential difference along this part of contour. From another side, Here , so is electric resistance of conductor. is electric voltage (drop voltage) for passive part of contour. On the active part of contour we have resulting electric field Equality occurs for integral values:

11. 6 a. Ohm’s law in the integral form Continue: , or E is external electromotive force. is the internal voltage drop at the active part of contour (i. e. inside of energy source) is an internal resistance of active part of contour (or source) Resulting form of Ohm’s law: E E E

11. 7. Specific heat conduction and specific heat capacity of electronic gas in metals Heat transfer in metals is provided mainly by electrons but not crystal lattice of atoms. Coefficient of heat conduction for electronic gas can be borrowed of classic theory of ideal gas: ; is a density of electron gas. Specific gas capacity c. V does not correspond to experiment for electronic gas. Instead the ratio is in a good agreement with experiment (Widemann and Franz law, 1853) At using the known formulae we obtain the ratio. (from quantum (classical theory) Lorentz number) Specific heat capacity of electron gas is very small in comparison with lattice’s one.