Electronic Griffiths phases and dissipative spin liquids E

Electronic Griffiths phases and dissipative spin liquids E. M. - Campinas, Brazil Darko Tanasković - Magnet Lab/FSU Vlad Dobrosavljević Complex Behavior in Correlated Electron Systems Lorentz Center – Leiden – August 11, 2005 1

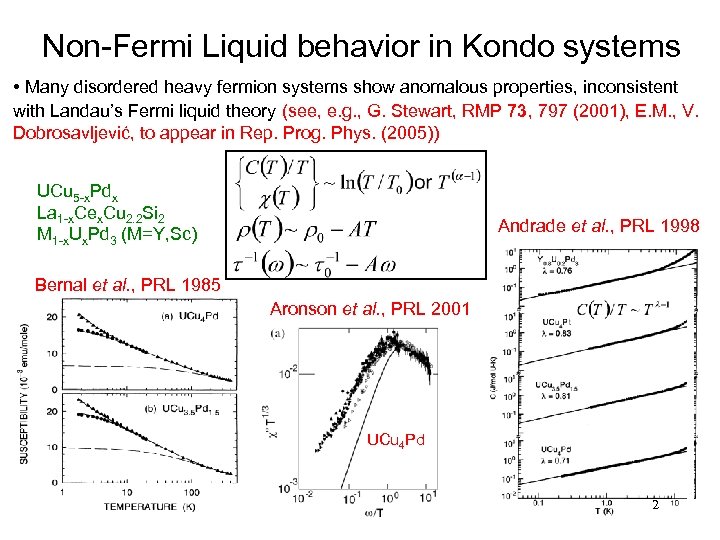Non-Fermi Liquid behavior in Kondo systems • Many disordered heavy fermion systems show anomalous properties, inconsistent with Landau’s Fermi liquid theory (see, e. g. , G. Stewart, RMP 73, 797 (2001), E. M. , V. Dobrosavljević, to appear in Rep. Prog. Phys. (2005)) UCu 5 -x. Pdx La 1 -x. Cex. Cu 2. 2 Si 2 M 1 -x. Ux. Pd 3 (M=Y, Sc) Andrade et al. , PRL 1998 Bernal et al. , PRL 1985 Aronson et al. , PRL 2001 UCu 4 Pd 2

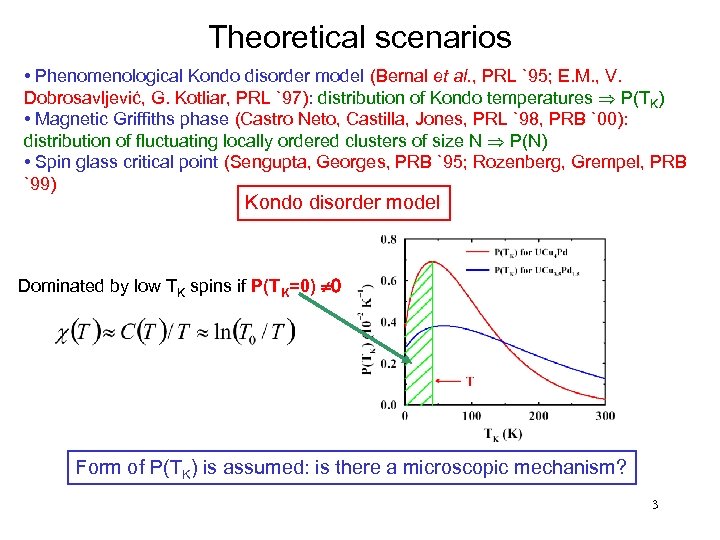Theoretical scenarios • Phenomenological Kondo disorder model (Bernal et al. , PRL `95; E. M. , V. Dobrosavljević, G. Kotliar, PRL `97): distribution of Kondo temperatures Þ P(TK) • Magnetic Griffiths phase (Castro Neto, Castilla, Jones, PRL `98, PRB `00): distribution of fluctuating locally ordered clusters of size N Þ P(N) • Spin glass critical point (Sengupta, Georges, PRB `95; Rozenberg, Grempel, PRB `99) Kondo disorder model Dominated by low TK spins if P(T K=0) ¹ 0 Form of P(TK) is assumed: is there a microscopic mechanism? 3

Electronic Griffiths phase (E. M. , V. Dobrosavljević, PRL `01) • Local DOS at the Fermi level (wave function amplitude) fluctuates spatially ® Anderson localization effects • T K is exponentially sensitive to the local DOS (Dobrosavljevic, Kirkpatrick, Kotliar, `92) • Statistical Dynamical Mean Field Theory (for the Anderson lattice) (Dobrosavljević, Kotliar, PRL `97) • A local correlated action at each f-site (U ® ¥ Anderson single-impurity model) Green’s function of conduction electrons with site “j” removed • Each f-site gives rise to a local self-energy Sj (wn) for the lattice problem, which is numerically solved 4

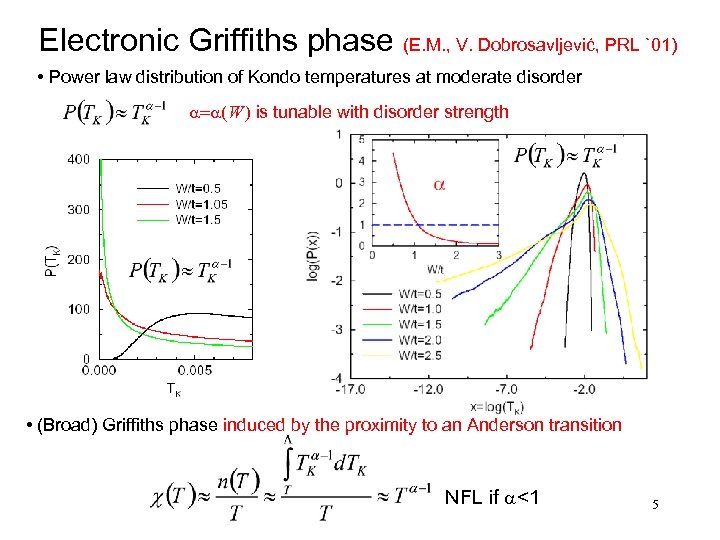Electronic Griffiths phase (E. M. , V. Dobrosavljević, PRL `01) • Power law distribution of Kondo temperatures at moderate disorder a=a(W ) is tunable with disorder strength • (Broad) Griffiths phase induced by the proximity to an Anderson transition NFL if a<1 5

Generic mechanism of quantum Griffiths phases • Exponentially rare events with exponentially low energy scales, e. g. , in a random field Ising model (D. Fisher, PRL `92, PRB `95) but also in other systems (Senthil, Sachdev, PRL `96; Castro Neto, Jones, PRB `00; T. Vojta, Schmalian, PRB `05; . . ) • For example, for a fluctuating ferromagnetic droplet of size V (Poisson) (tunneling) Power-law distribution of energy scales (tunneling rates) • From this, the usual phenomenology follows, quite independent of the nature of the fluctuators 6

What is the origin of the electronic GP? • Effective model (D. Tanasković, V. Dobrosavljević, E. M. , PRB `04) Model with c-site (diagonal) disorder only and Gaussian distribution • Infinite coordination limit (z ® ¥) (Dynamical Mean Field Theory) • No DOS fluctuations (no Anderson localization effects)! Fixed conduction electron bath 7

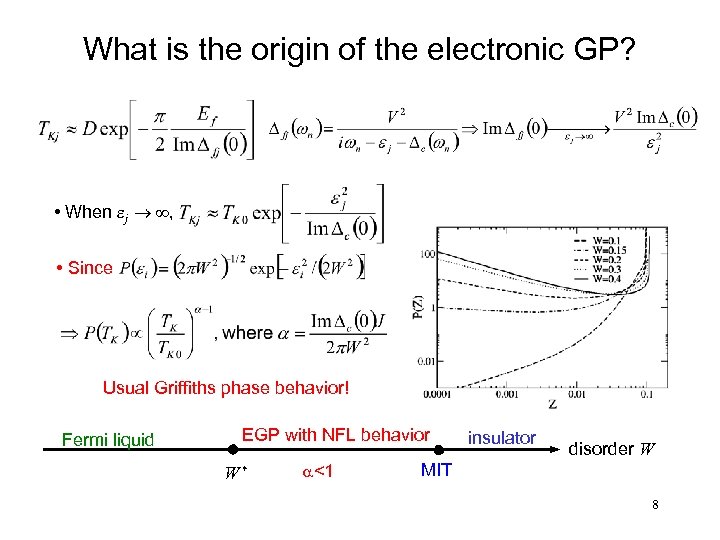What is the origin of the electronic GP? • When ej ® ¥, • Since Usual Griffiths phase behavior! Fermi liquid EGP with NFL behavior W* a<1 insulator disorder W MIT 8

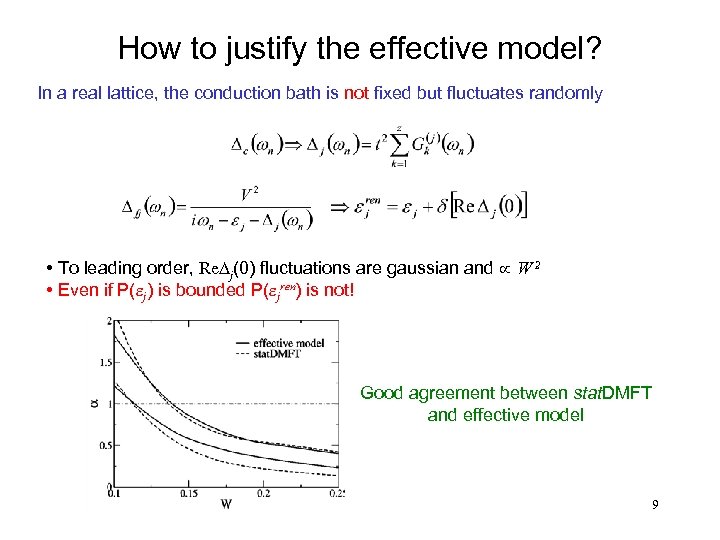How to justify the effective model? In a real lattice, the conduction bath is not fixed but fluctuates randomly • To leading order, Re. Dj(0) fluctuations are gaussian and µ W 2 • Even if P(ej) is bounded P(ejren) is not! Good agreement between stat. DMFT and effective model 9

Problems with the usual scenario • Thermodynamic divergences are too strong a» 1/W 2; experiments show near log behavior (a» 1). • Proliferation of “free” spins: entropy expected to be quenched by interactions at low T, (probably spin-glass, D. Mac. Laughlin et al. PRL `01) What is missing? • RKKY interactions between (distant) low-T K (unscreened) spins: oscillatory with distance Þ random in magnitude and sign • Expect quantum spin-glass dynamics at low T (D. Mac. Laughlin et al. PRL`01) • (E)DMFT formulation: infinite-range spin glass interactions (paramagnetic phase) (Tanasković, Dobrosavljević, E. M. , cond-mat/0412100) • Self-consistency: • Local action: “Bose-Fermi Kondo model” Related work: Burdin, Grempel, Georges, PRB ´ 02 10

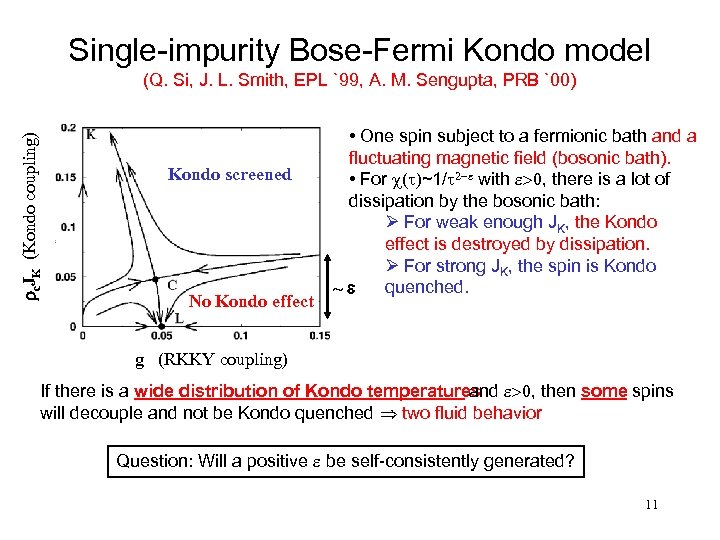Single-impurity Bose-Fermi Kondo model rc. JK (Kondo coupling) (Q. Si, J. L. Smith, EPL `99, A. M. Sengupta, PRB `00) Kondo screened No Kondo effect • One spin subject to a fermionic bath and a fluctuating magnetic field (bosonic bath). • For c(t)~1/t 2 -e with e>0, there is a lot of dissipation by the bosonic bath: Ø For weak enough JK, the Kondo effect is destroyed by dissipation. Ø For strong JK, the spin is Kondo quenched. ~e g (RKKY coupling) If there is a wide distribution of Kondo temperatures e>0, then some spins and will decouple and not be Kondo quenched Þ two fluid behavior Question: Will a positive e be self-consistently generated? 11

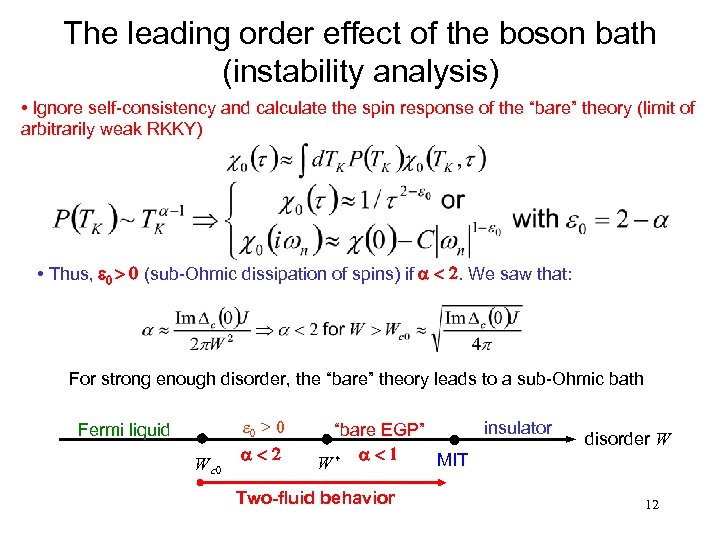The leading order effect of the boson bath (instability analysis) • Ignore self-consistency and calculate the spin response of the “bare” theory (limit of arbitrarily weak RKKY) • Thus, e 0 > 0 (sub-Ohmic dissipation of spins) if a < 2. We saw that: For strong enough disorder, the “bare” theory leads to a sub-Ohmic bath e 0 > 0 Fermi liquid W c 0 a<2 insulator “bare EGP” MIT W* a < 1 Two-fluid behavior disorder W 12

How will full self-consistency change this? Additive contributions from each fluid: Suppose the self-consistent bath goes like • Decoupled spins: (Sengupta, `00; Zhu, Si, PRB `02; Zaránd, Demler, PRB ´ 02) • Quenched spins: where n(e) is the “correlation time exponent” of the Bose-Fermi transition Clearly, edc>e. K Þ decoupled spins dominate at low frequencies 13

Self-consistency Imposing self-consistency: Þ Sachdev-Ye spin liquid (PRL `93) Numerical results using large-N methods to solve the singleimpurity problems: • Marginal behavior over many decades Fermi liquid W 1 NFL spin liquid insulator e 0 > 0 W * “bare EGP” MIT Two-fluid behavior disorder W 14

Other consequences • n(e) » e/2 + O(e 2) » 1/2 Þ • Resistivity from the decoupled part: marginal Fermi liquid • Low temperature spin-glass instability: Estimated from Large window with marginal behavior above Tg 15

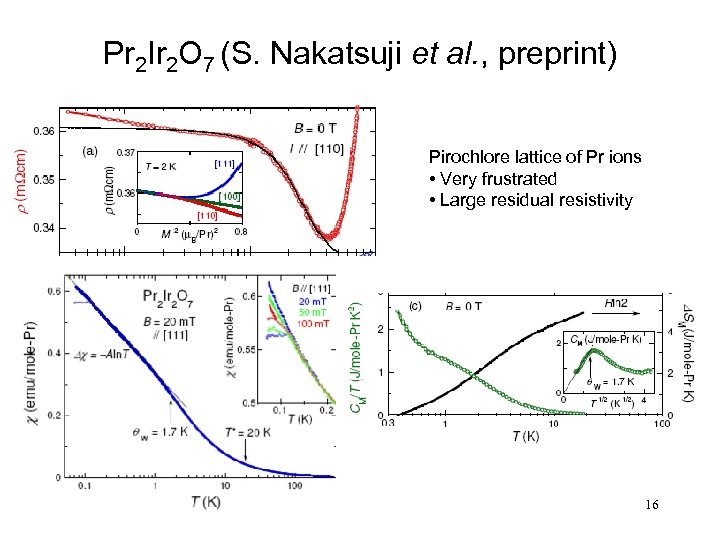Pr 2 Ir 2 O 7 (S. Nakatsuji et al. , preprint) Pirochlore lattice of Pr ions • Very frustrated • Large residual resistivity 16

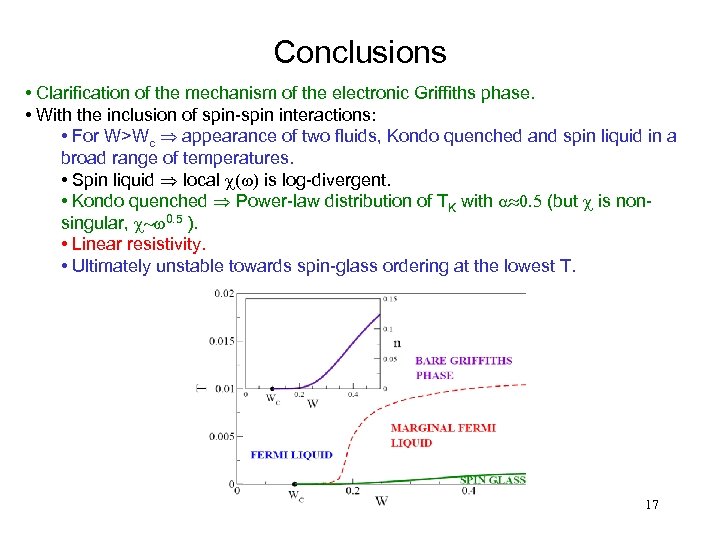Conclusions • Clarification of the mechanism of the electronic Griffiths phase. • With the inclusion of spin-spin interactions: • For W>Wc Þ appearance of two fluids, Kondo quenched and spin liquid in a broad range of temperatures. • Spin liquid Þ local c(w) is log-divergent. • Kondo quenched Þ Power-law distribution of TK with a» 0. 5 (but c is nonsingular, c~w 0. 5 ). • Linear resistivity. • Ultimately unstable towards spin-glass ordering at the lowest T. 17