Electrohydrodynamic instabilities in microfluidics Brian D Storey Franklin

Electrohydrodynamic instabilities in microfluidics Brian D. Storey Franklin W. Olin College of Engineering Needham MA

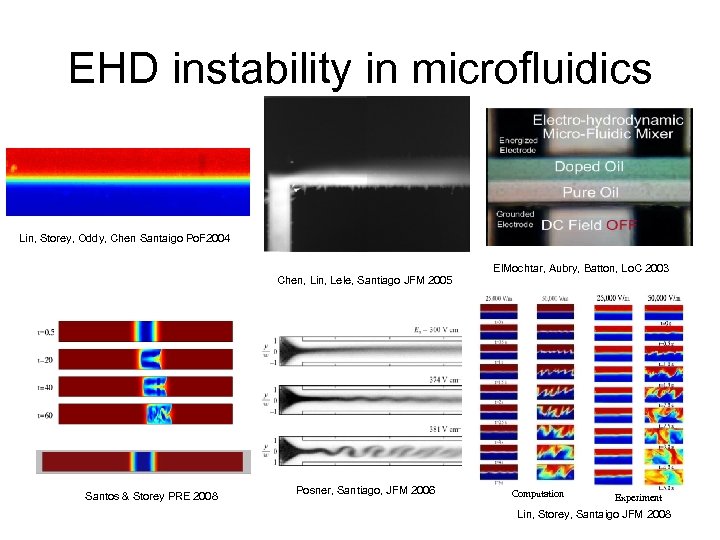
EHD instability in microfluidics Lin, Storey, Oddy, Chen Santaigo Po. F 2004 Chen, Lin, Lele, Santiago JFM 2005 Santos & Storey PRE 2008 Posner, Santiago, JFM 2006 El. Mochtar, Aubry, Batton, Lo. C 2003 Computation Experiment Lin, Storey, Santaigo JFM 2008

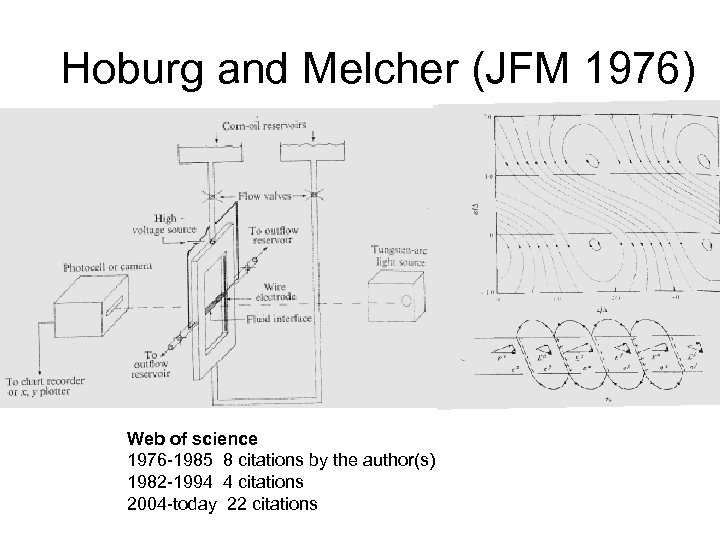
Hoburg and Melcher (JFM 1976) Web of science 1976 -1985 8 citations by the author(s) 1982 -1994 4 citations 2004 -today 22 citations

Electrohydrodynamics • Electrohydrodynamics is the interaction between electric fields and fluid motion. • Today we will be concerned with EHD of simple, miscible, electrolytes.

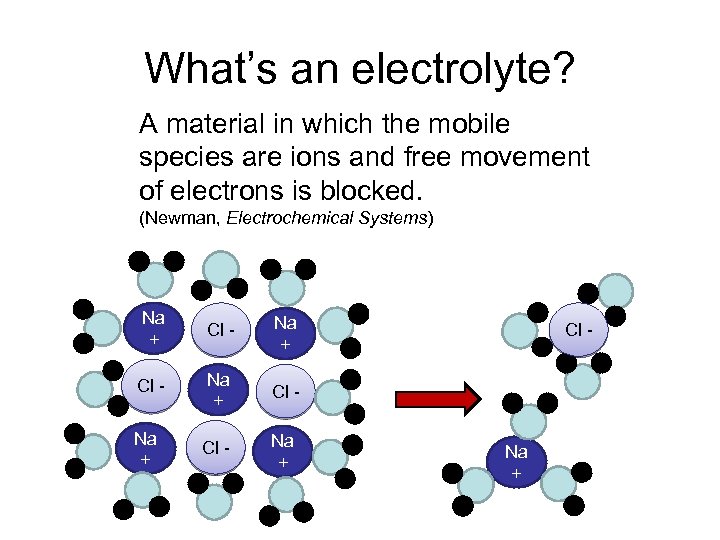
What’s an electrolyte? A material in which the mobile species are ions and free movement of electrons is blocked. (Newman, Electrochemical Systems) Na + Cl - Na + Cl - Na +

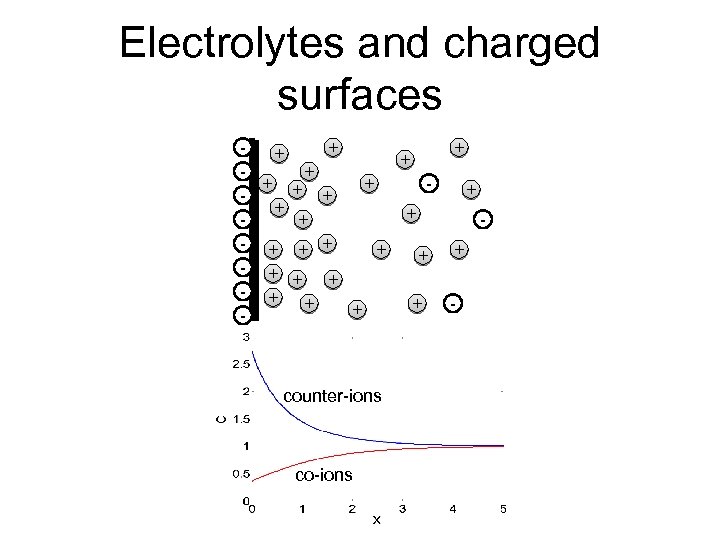
Electrolytes and charged surfaces + + + - + + + + - counter-ions co-ions + + + -

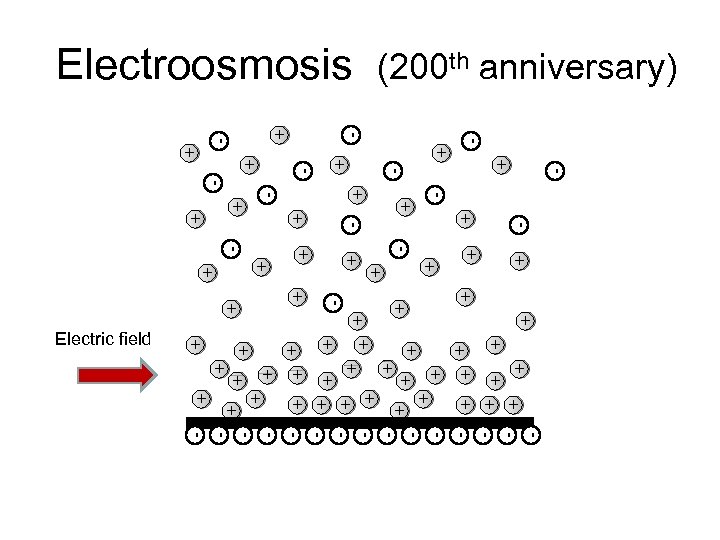
Electric field + + + + + + - + + + + + - + + + + - - - + - + + + - - + - Electroosmosis (200 th anniversary)

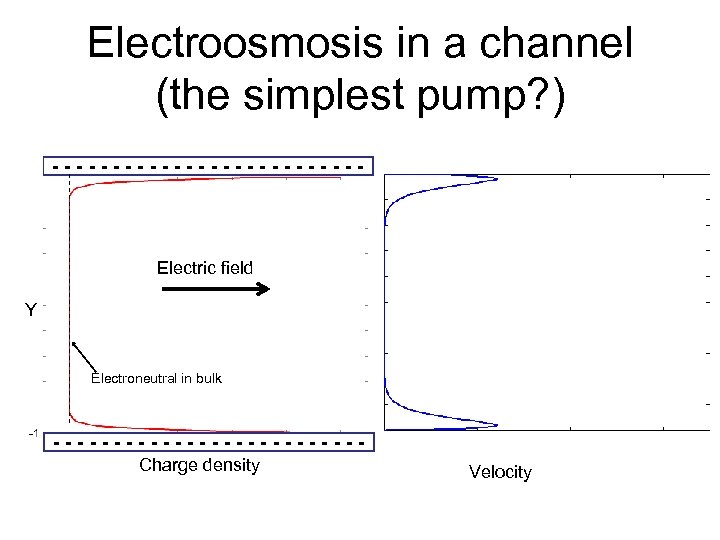
Electroosmosis in a channel (the simplest pump? ) ------------- Y Electric field Y Electroneutral in bulk -------------Charge density Velocity

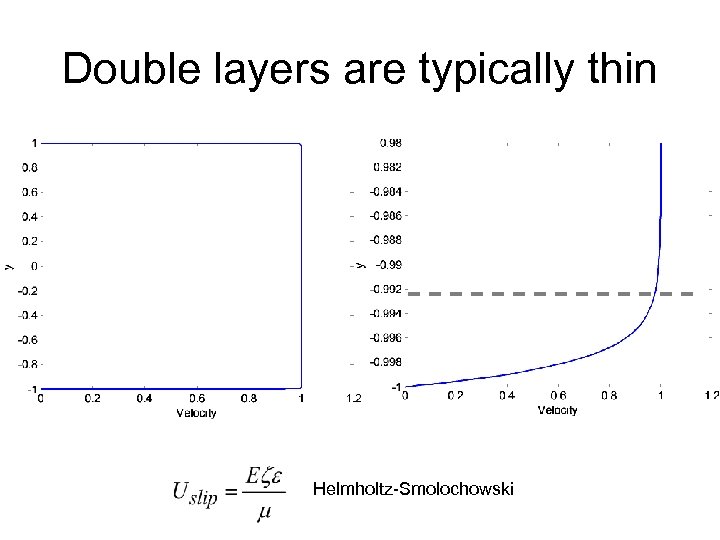
Double layers are typically thin Helmholtz-Smolochowski

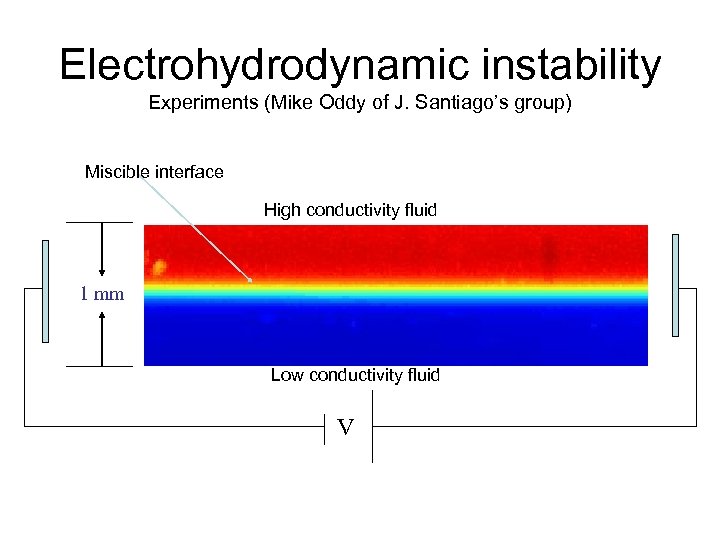
Electrohydrodynamic instability Experiments (Mike Oddy of J. Santiago’s group) Miscible interface High conductivity fluid 1 mm Low conductivity fluid V

Model summary • Incompressible Navier-Stokes plus electric body force • Poisson-Nernst-Planck for ion transport binary, symmetric electrolyte; simplified by assuming fluid is nearly electro-neutral. • Helmholtz-Smolochowski electrokinetic slip boundary conditions m a=F Mass is conserved Fluid conductivity goes with the flow Current is conserved, V=i. R Lin, Storey, Oddy, Chen Santaigo Po. F 2004

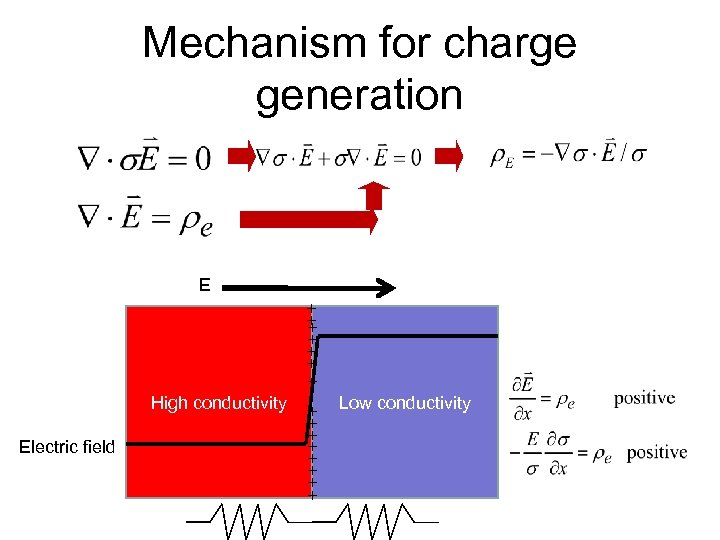
Mechanism for charge generation E + + + + High conductivity Electric field + + + + Low conductivity

Mechanism for flow E

Dimensionless parameters Electric Rayleigh number Reynolds number Electrical conductivity ratio Ratio of electro-osmotic to electroviscous velocity

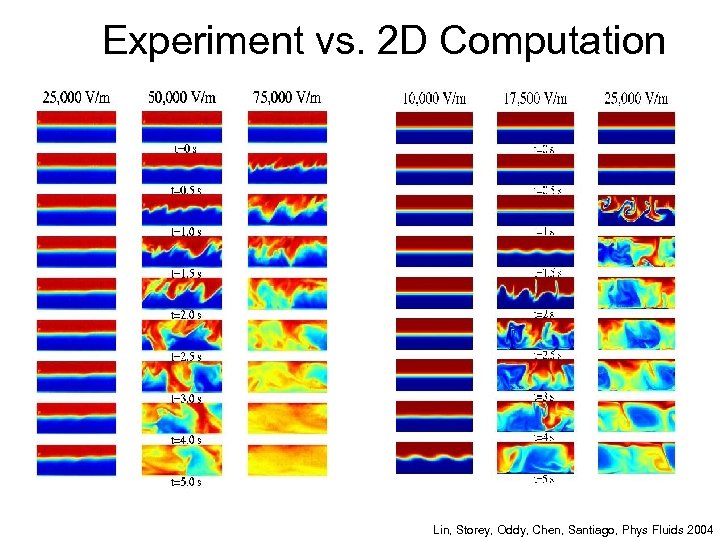
Experiment vs. 2 D Computation Lin, Storey, Oddy, Chen, Santiago, Phys Fluids 2004

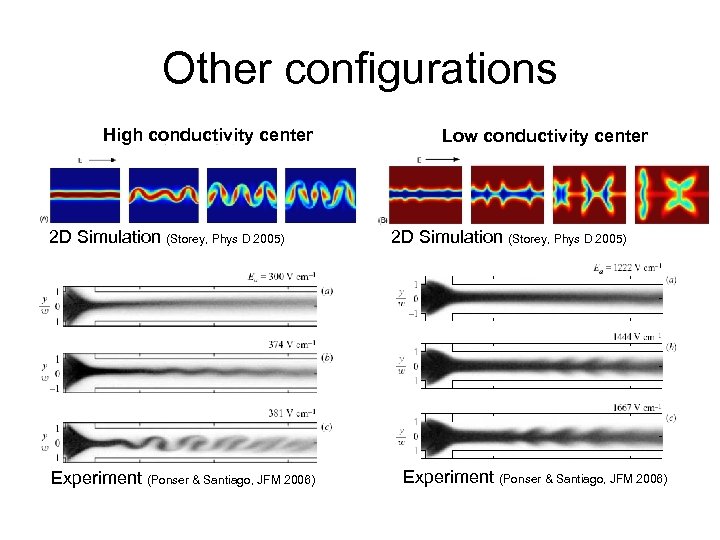
Other configurations High conductivity center 2 D Simulation (Storey, Phys D 2005) Experiment (Ponser & Santiago, JFM 2006) Low conductivity center 2 D Simulation (Storey, Phys D 2005) Experiment (Ponser & Santiago, JFM 2006)

Instability at T-junction 0. 5, 0. 75, 1, & 1. 25 k. V/cm Simulations with same basic model provided good agreement Chen, Lin, Lele, & Santiago, JFM 2005

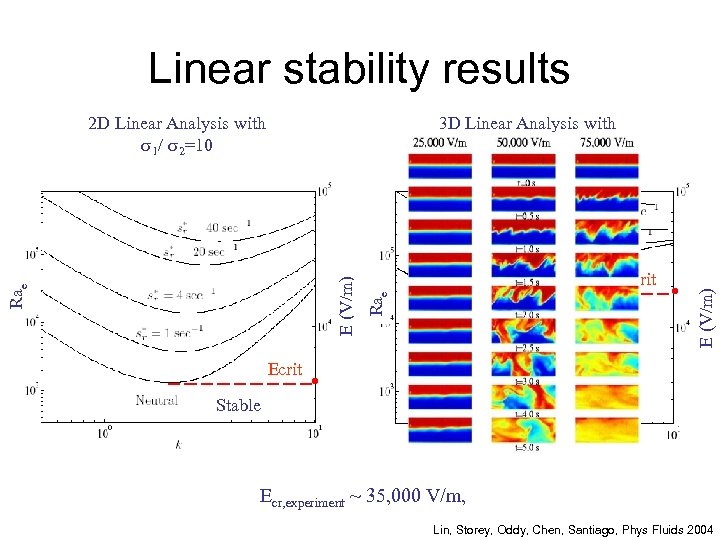
Linear stability results 2 D Linear Analysis with 1/ 2=10 3 D Linear Analysis with 1/ 2=10 Ecrit Stable E (V/m) y x Rae E (V/m) z Ecrit Stable Ecr, experiment ~ 35, 000 V/m, Lin, Storey, Oddy, Chen, Santiago, Phys Fluids 2004

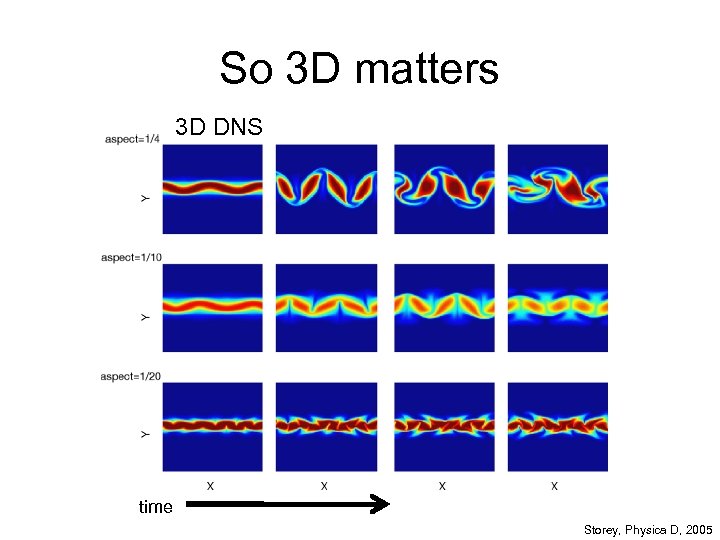
So 3 D matters 3 D DNS time Storey, Physica D, 2005

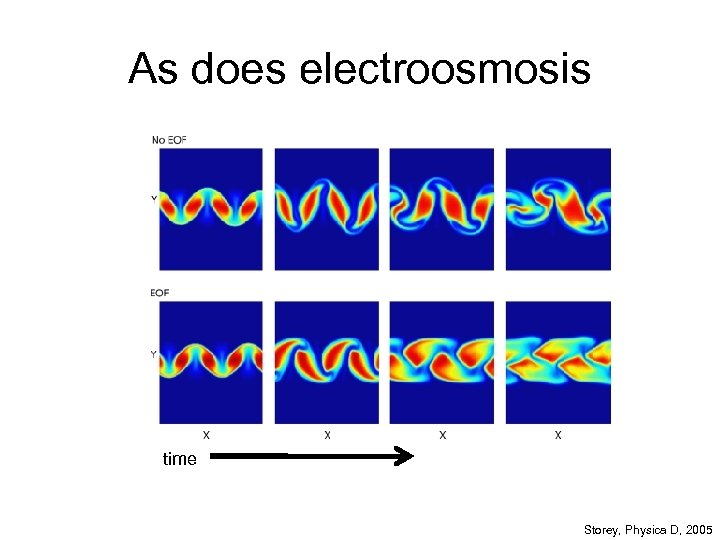
As does electroosmosis time Storey, Physica D, 2005

Thin channels • So aspect ratio matters, but can we model flow in thin channels with a 2 D model? z y H x d 2 E 1

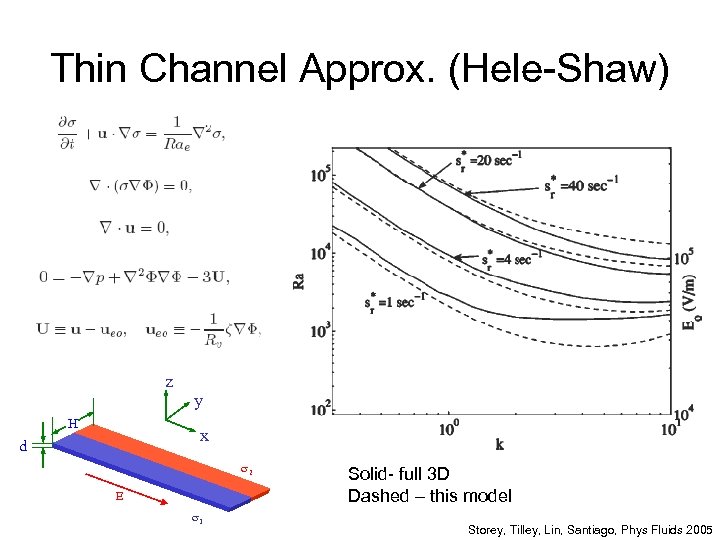
Thin Channel Approx. (Hele-Shaw) z H y x d 2 E 1 Solid- full 3 D Dashed – this model Storey, Tilley, Lin, Santiago, Phys Fluids 2005

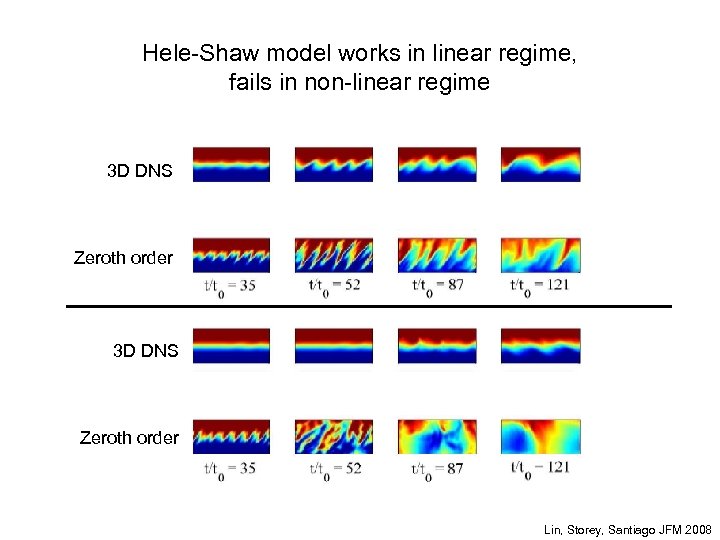
Hele-Shaw model works in linear regime, fails in non-linear regime 3 D DNS Depth Ave Zeroth order Lin, Storey, Santiago JFM 2008

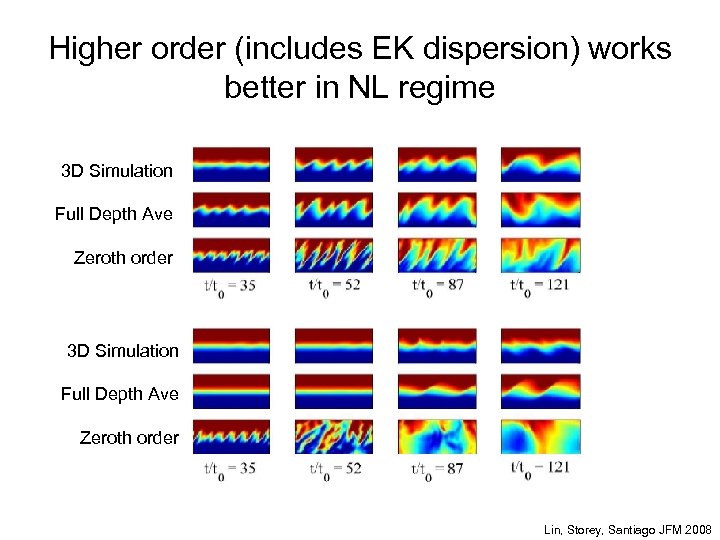
Higher order (includes EK dispersion) works better in NL regime 3 D Simulation Full Depth Ave Zeroth order Lin, Storey, Santiago JFM 2008

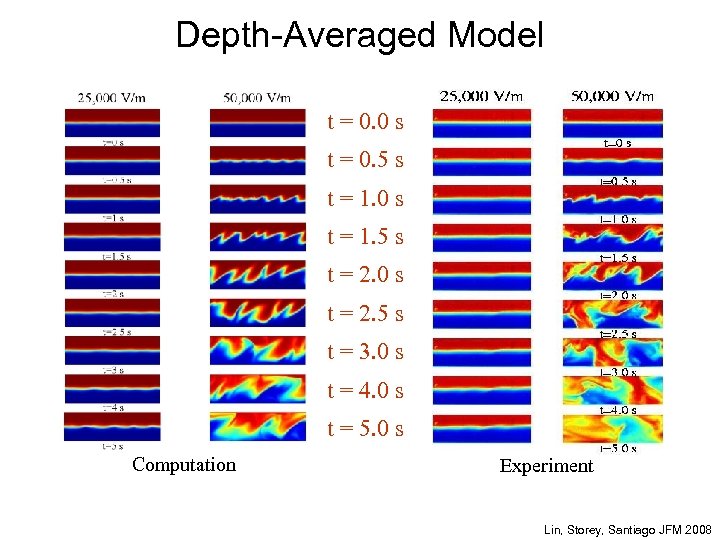
Depth-Averaged Model t = 0. 0 s t = 0. 5 s t = 1. 0 s t = 1. 5 s t = 2. 0 s t = 2. 5 s t = 3. 0 s t = 4. 0 s t = 5. 0 s Computation Experiment Lin, Storey, Santiago JFM 2008

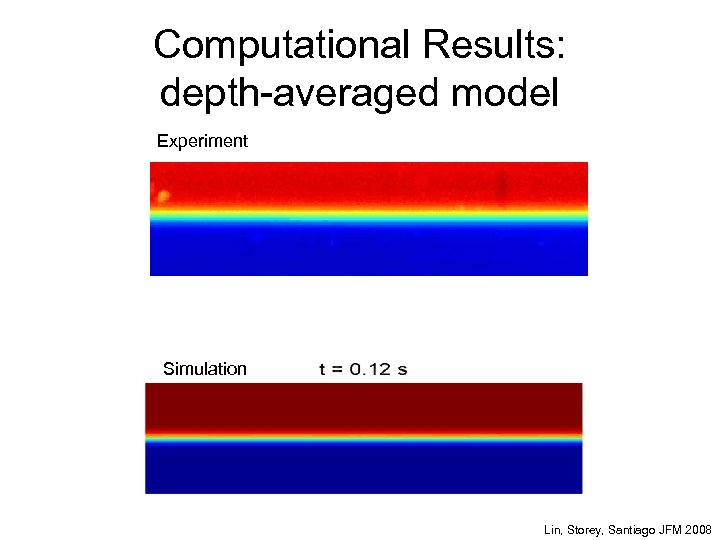
Computational Results: depth-averaged model Experiment Simulation Lin, Storey, Santiago JFM 2008

So… • Depth averaged, 2 D model for electrokinetic flow works. • Need to include electrokinetic dispersion in the model. • But what’s electrokinetic dispersion?

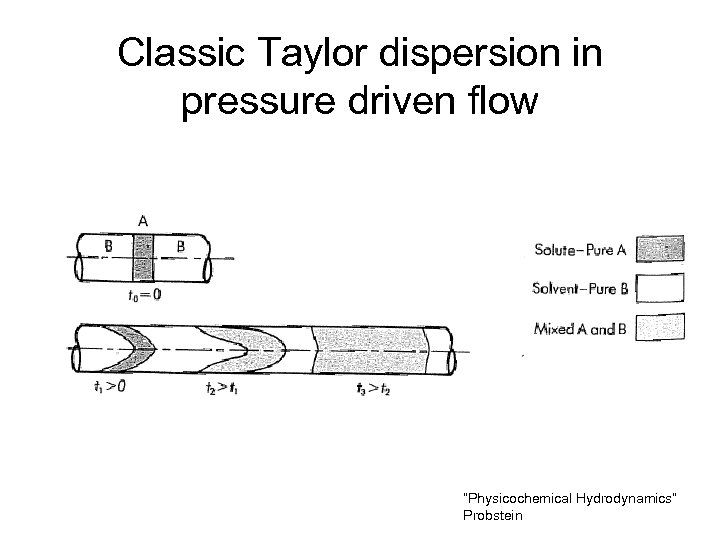
Classic Taylor dispersion in pressure driven flow “Physicochemical Hydrodynamics” Probstein

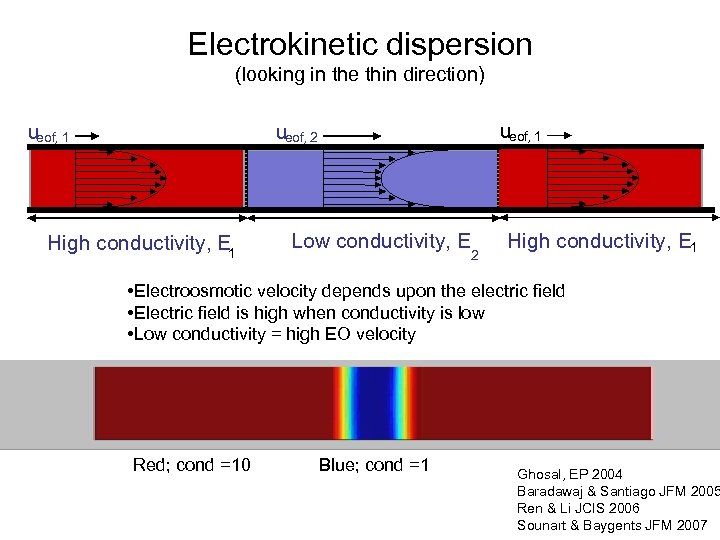
Electrokinetic dispersion (looking in the thin direction) ueof, 1 ueof, 2 High conductivity, E 1 Low conductivity, E 2 High conductivity, E 1 • Electroosmotic velocity depends upon the electric field • Electric field is high when conductivity is low • Low conductivity = high EO velocity Red; cond =10 Blue; cond =1 Ghosal, EP 2004 Baradawaj & Santiago JFM 2005 Ren & Li JCIS 2006 Sounart & Baygents JFM 2007

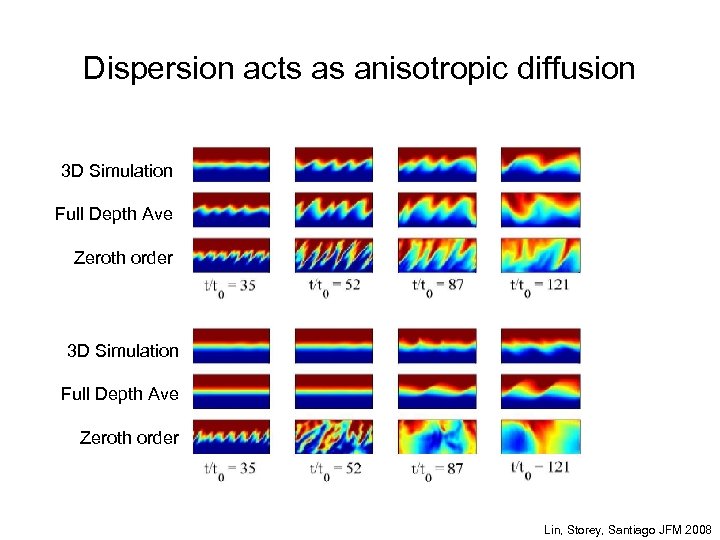
Dispersion acts as anisotropic diffusion 3 D Simulation Full Depth Ave Zeroth order Lin, Storey, Santiago JFM 2008

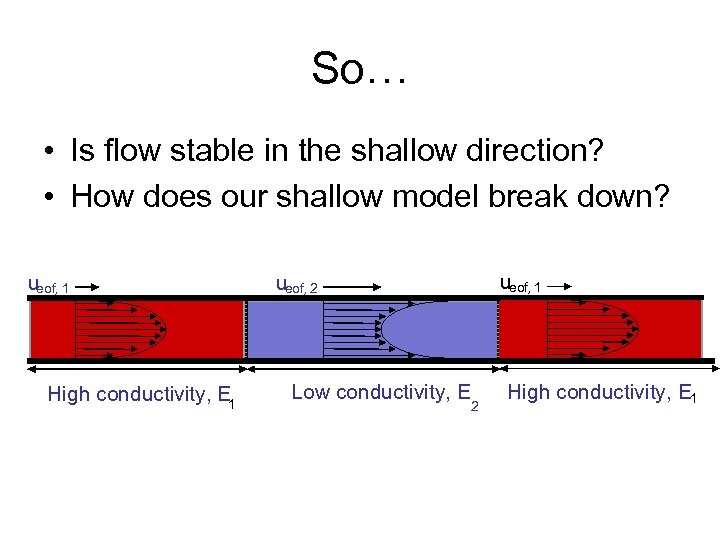
So… • Is flow stable in the shallow direction? • How does our shallow model break down? ueof, 1 High conductivity, E 1 ueof, 2 Low conductivity, E 2 High conductivity, E 1

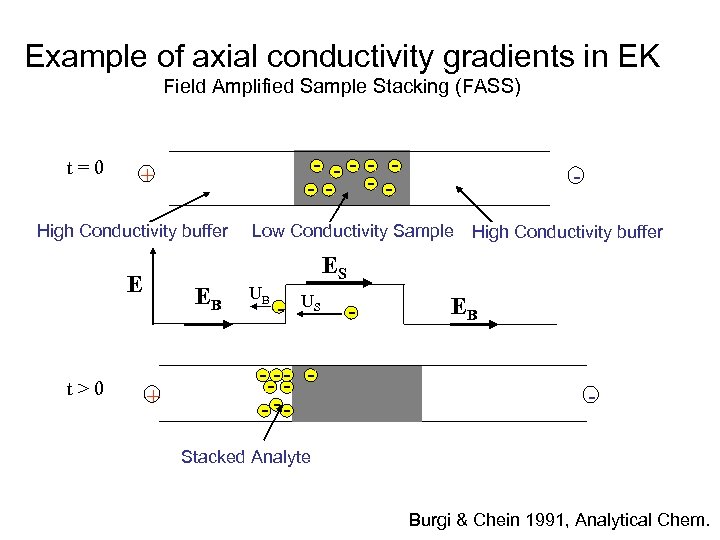
Example of axial conductivity gradients in EK Field Amplified Sample Stacking (FASS) t=0 - -- - - + High Conductivity buffer Low Conductivity Sample High Conductivity buffer ES E t>0 - EB + UB - US --- - - -- - EB - Stacked Analyte Burgi & Chein 1991, Analytical Chem.

Unstable flow E=25, 000 V/m, Conductivity ratio=10 Santos & Storey, PRE 2008

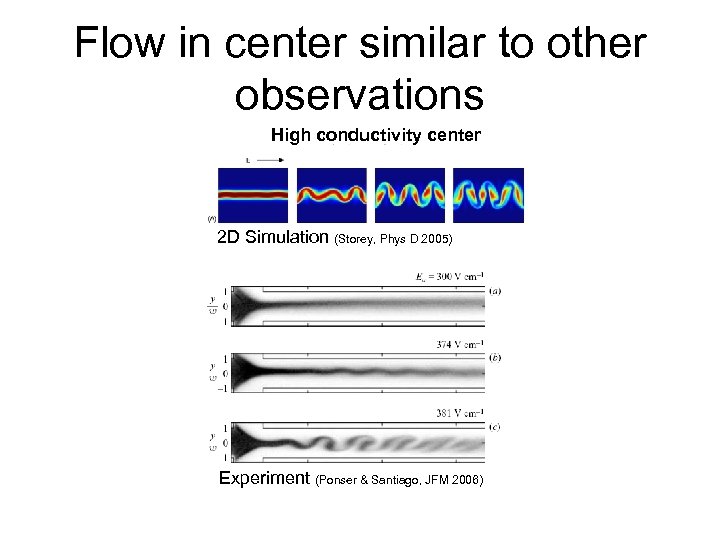
Flow in center similar to other observations High conductivity center 2 D Simulation (Storey, Phys D 2005) Experiment (Ponser & Santiago, JFM 2006)

Observations • “Shock” at the leading edge of the sample. • Vertical velocity at the channel walls pumps fluid toward the centerline. • Unstable flow only inside the sample region. Santos & Storey, PRE 2008

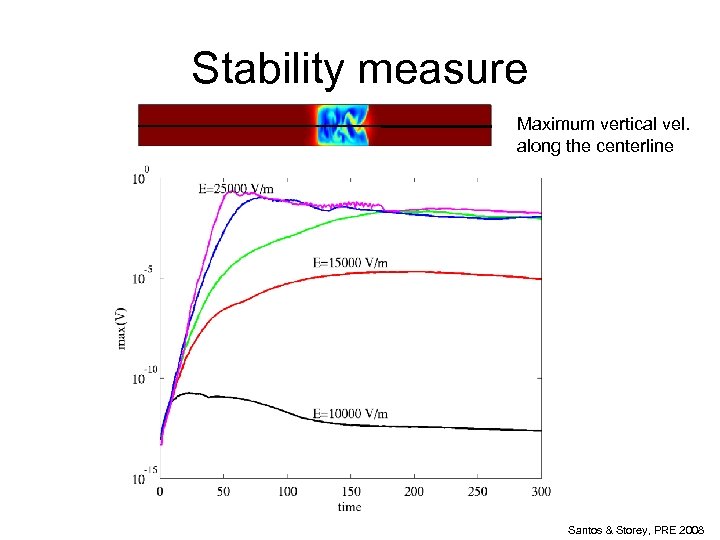
Stability measure Maximum vertical vel. along the centerline Santos & Storey, PRE 2008

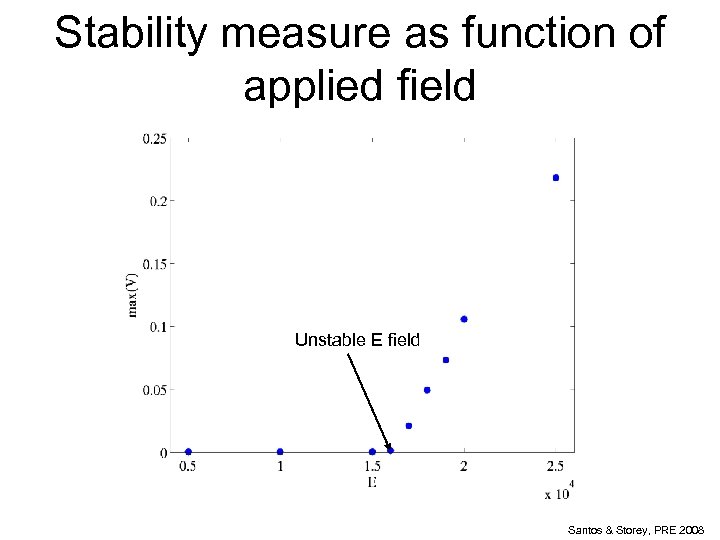
Stability measure as function of applied field Unstable E field Santos & Storey, PRE 2008

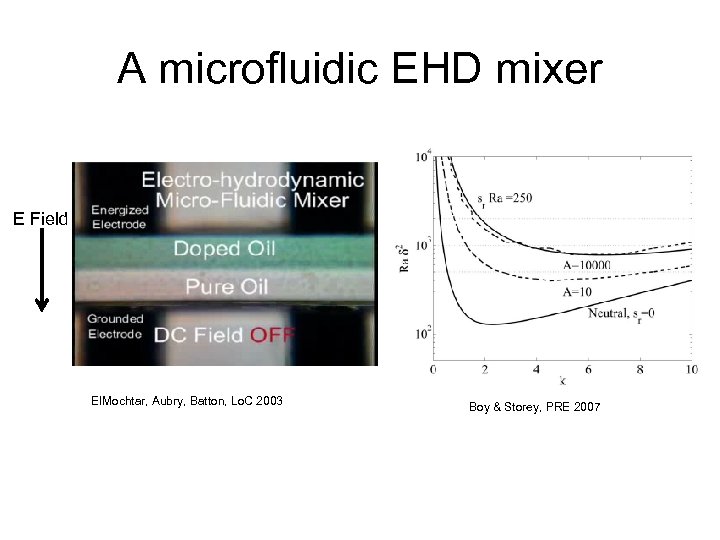
A microfluidic EHD mixer E Field El. Mochtar, Aubry, Batton, Lo. C 2003 Boy & Storey, PRE 2007

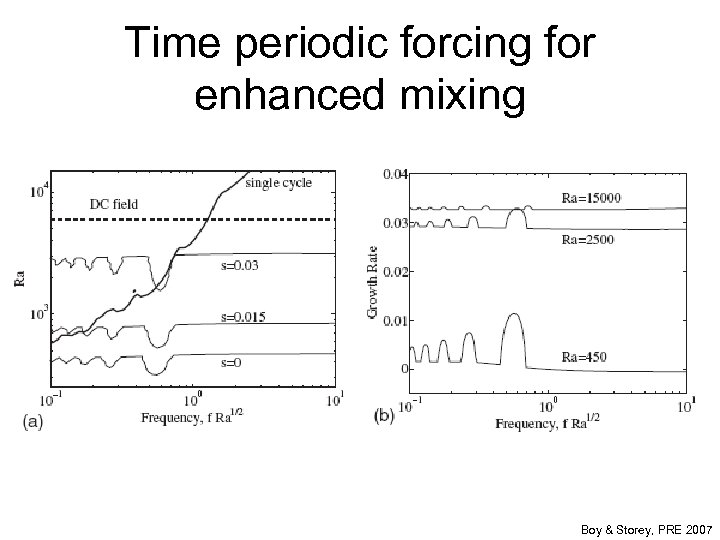
Time periodic forcing for enhanced mixing Boy & Storey, PRE 2007

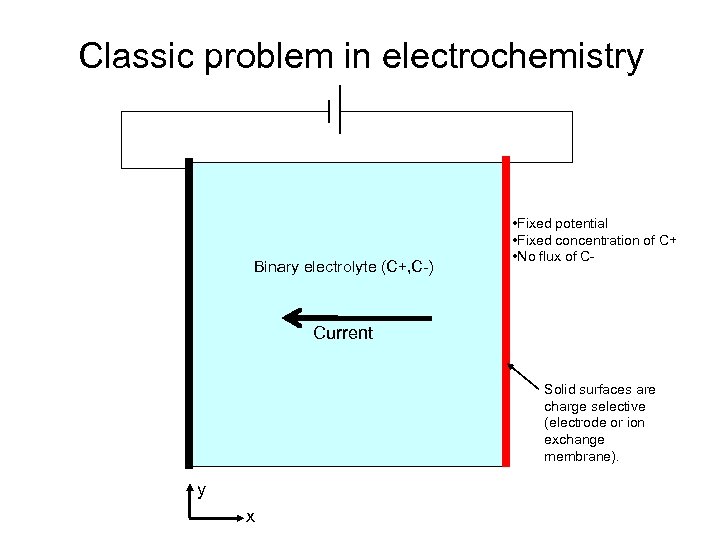
Classic problem in electrochemistry Binary electrolyte (C+, C-) • Fixed potential • Fixed concentration of C+ • No flux of C- Current Solid surfaces are charge selective (electrode or ion exchange membrane). y x

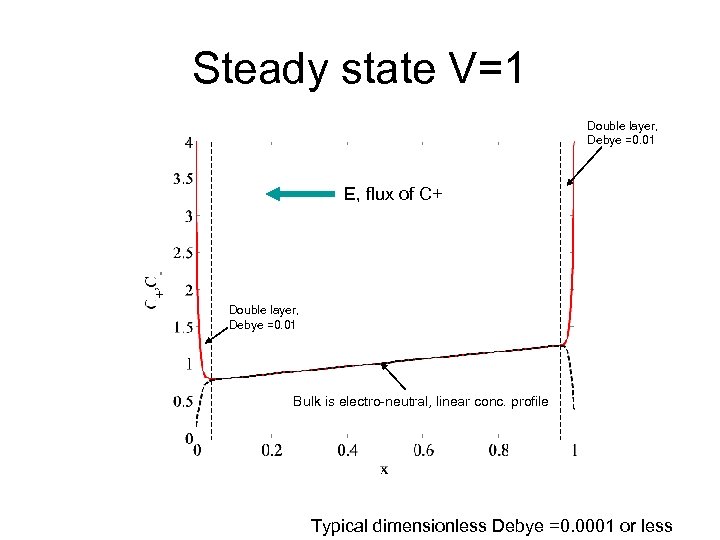
Steady state V=1 Double layer, Debye =0. 01 E, flux of C+ Double layer, Debye =0. 01 Bulk is electro-neutral, linear conc. profile Typical dimensionless Debye =0. 0001 or less

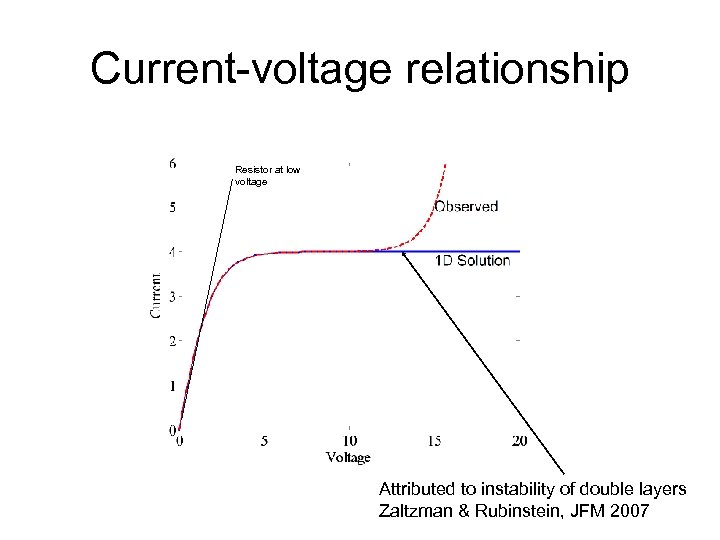
Current-voltage relationship Resistor at low voltage Attributed to instability of double layers Zaltzman & Rubinstein, JFM 2007

Different views on bulk stability • Bulk instability. Grigin (1985, 1992) • Bulk instability, but not sufficient for mixing. Bruinsma & Alexander (1990) • Bulk instability. Rubinstein, Zaltzman, & Zaltzman (1995). • No bulk instability. Buchanan & Saville (1999) • No bulk instability. Highlighted problems with all earlier works reporting instability. Limited parameter space. Lerman, Zaltzman, Rubinstein (2005) Q: The model equations for bulk instability is the same as ours, why is there no bulk instability? Or is there?

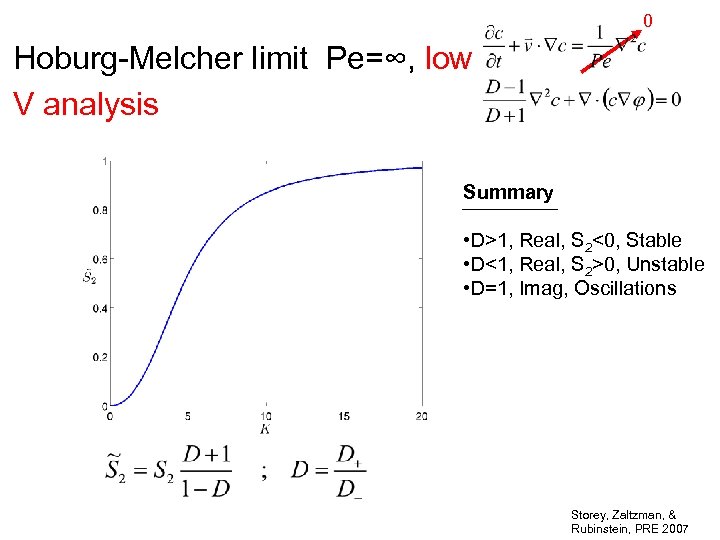
0 Hoburg-Melcher limit Pe=∞, low V analysis Summary • D>1, Real, S 2<0, Stable • D<1, Real, S 2>0, Unstable • D=1, Imag, Oscillations Storey, Zaltzman, & Rubinstein, PRE 2007

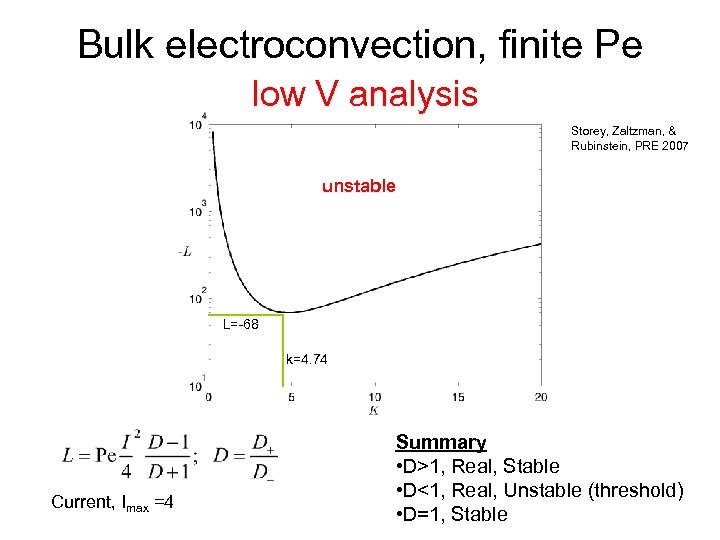
Bulk electroconvection, finite Pe low V analysis Storey, Zaltzman, & Rubinstein, PRE 2007 unstable L=-68 k=4. 74 Current, Imax =4 Summary • D>1, Real, Stable • D<1, Real, Unstable (threshold) • D=1, Stable

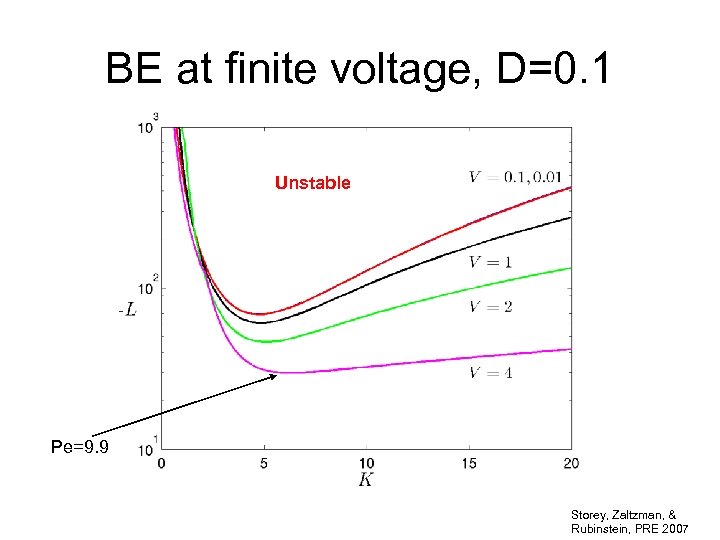
BE at finite voltage, D=0. 1 Unstable Pe=9. 9 Storey, Zaltzman, & Rubinstein, PRE 2007

Relationship between BE and microchannel EHD instability • Bulk instability can exist, in theory. • Threshold is different since conductivity gradient is driven • New bulk instability mechanism found when D+ < D-, that can occur at low V. • Many previous studies only considered D+=D. • An analysis looking for an application…

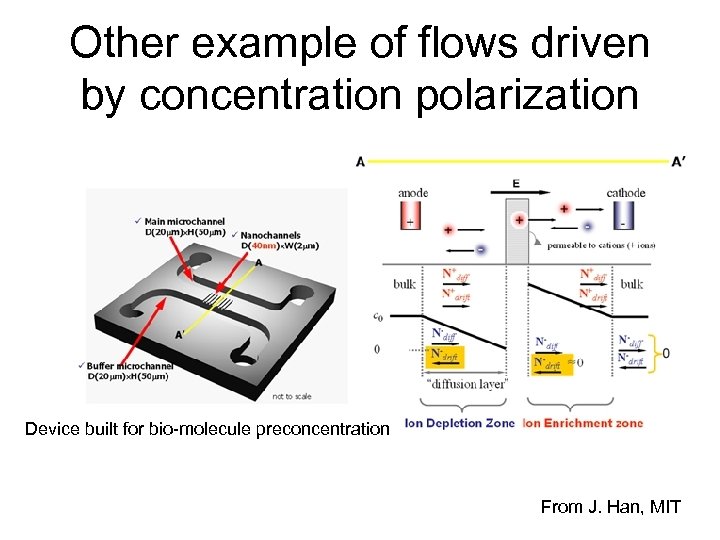
Other example of flows driven by concentration polarization Device built for bio-molecule preconcentration From J. Han, MIT

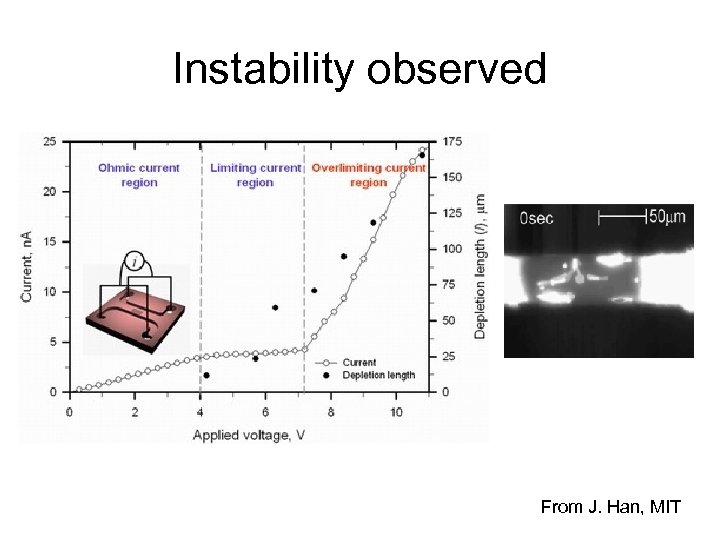
Instability observed From J. Han, MIT

Stuff I didn’t show you. . Colloids, Posner Two phase, Zahn & Reddy Electrothermal, Ramos, Gonzalez, Castellanos, et al Two phase, Aubry et al Multi-species, Oddy & Santiago

Acknowledgements • • • Collaborators: – Hao Lin, Rutgers – Juan Santiago, Stanford – Boris Zaltzman & Isaac Rubinstein, Ben Gurion University of Negev, Israel Undergraduate students – David Boy – Jobim Santos – Lee Edwards – Doug Ellwanger – Allison Schmidt – Mark Cavolowsky – Nina Cary – Angela Mao Funding – NSF – Olin College

Depth averaged equations From the DA equations, we can reconstruct the full 3 D fields.