Electroanalytical chemistry Potentiometry Voltammetry and Polarography Electroanalysis

Electroanalytical chemistry Potentiometry, Voltammetry and Polarography

Electroanalysis • measure the variation of an electrical parameter (potential, current, charge, conductivity) and relate this to a chemical parameter (the analyte concentration) • Conductimetry, potentiometry (p. H, ISE), coulometry, voltammetry

Potentiometry the measure of the cell potential to yield chemical information (conc. , activity, charge) Measure difference in potential between two electrodes: reference electrode (E constant) indicator electrode (signal α analyte)

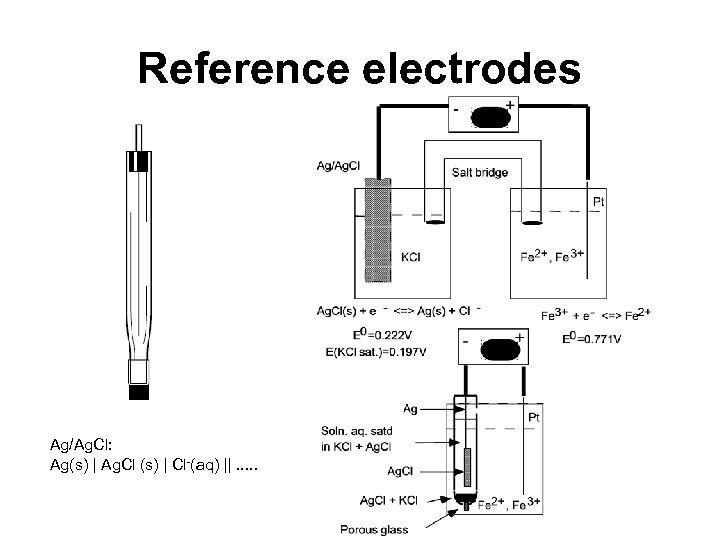Reference electrodes Ag/Ag. Cl: Ag(s) | Ag. Cl (s) | Cl-(aq) ||. . .

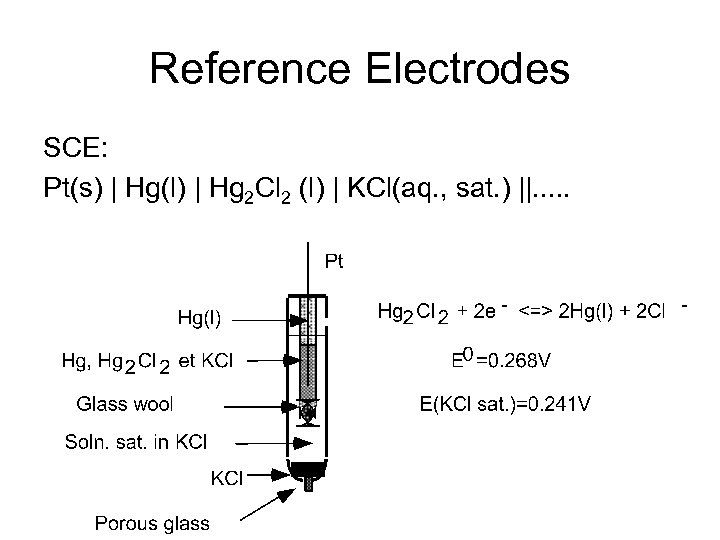Reference Electrodes SCE: Pt(s) | Hg(l) | Hg 2 Cl 2 (l) | KCl(aq. , sat. ) ||. . .

Indicator Electrodes • Inert: Pt, Au, Carbon. Don’t participate in the reaction. example: SCE || Fe 3+, Fe 2+(aq) | Pt(s) • Certain metallic electrodes: detect their ions (Hg, Cu, Zn, Cd, Ag) example SCE || Ag+(aq) | Ag(s) Ag+ + e- Ag(s) E 0+= 0. 799 V Hg 2 Cl 2 + 2 e 2 Hg(l) + 2 Cl. E-= 0. 241 V E = 0. 799 + 0. 05916 log [Ag+] - 0. 241 V

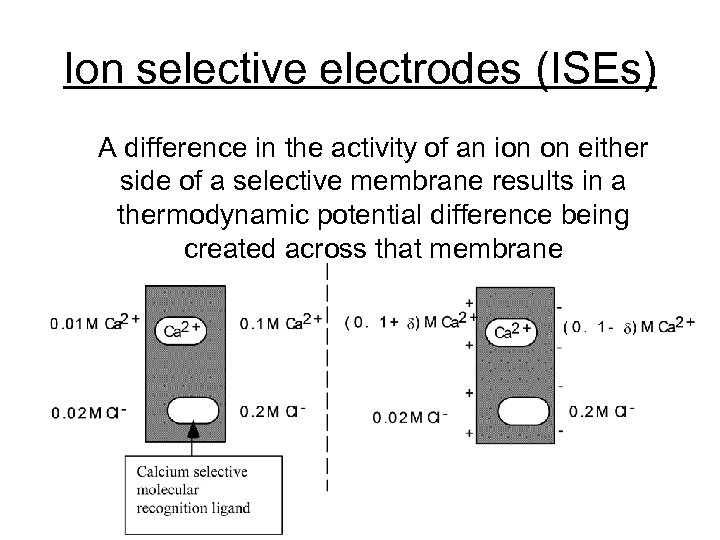Ion selective electrodes (ISEs) A difference in the activity of an ion on either side of a selective membrane results in a thermodynamic potential difference being created across that membrane

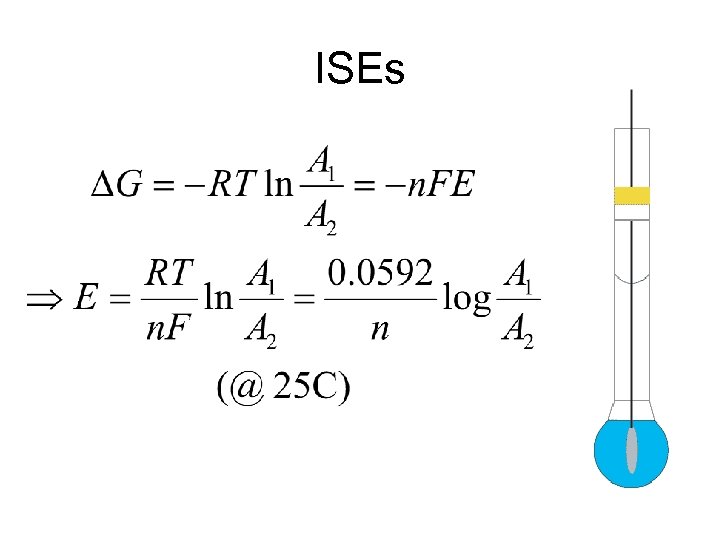ISEs

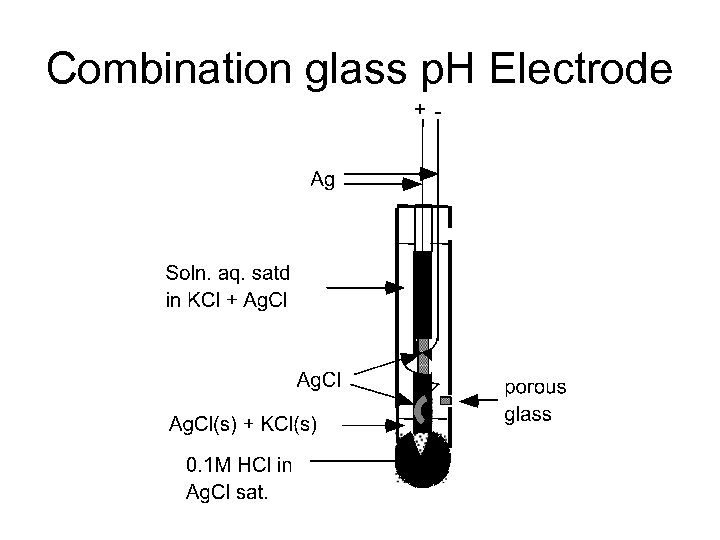Combination glass p. H Electrode

Proper p. H Calibration • E = constant – constant. 0. 0591 p. H • Meter measures E vs p. H – must calibrate both slope & intercept on meter with buffers • Meter has two controls – calibrate & slope • 1 st use p. H 7. 00 buffer to adjust calibrate knob • 2 nd step is to use any other p. H buffer • Adjust slope/temp control to correct p. H value • This will pivot the calibration line around the isopotential which is set to 7. 00 in all meters Slope/temp control pivots line around isopotential without changing it m. V Calibrate knob raises and lowers the line without changing slope 4 7 p. H

Liquid Membrane Electrodes

Solid State Membrane Electrodes Ag wire Filling solution with fixed [Cl-] and cation that electrode responds to Ag/Ag. Cl Solid state membrane (must be ionic conductor) Solid State Membrane Chemistry Membrane Ion Determined La. F 3 F-, La 3+ Ag. Cl Ag+, Cl. Ag. Br Ag+, Br. Ag. I Ag+, IAg 2 S Ag+, S 2 Ag 2 S + Cu. S Cu 2+ Ag 2 S + Cd. S Cd 2+ Ag 2 S + Pb. S Pb 2+

Solid state electrodes

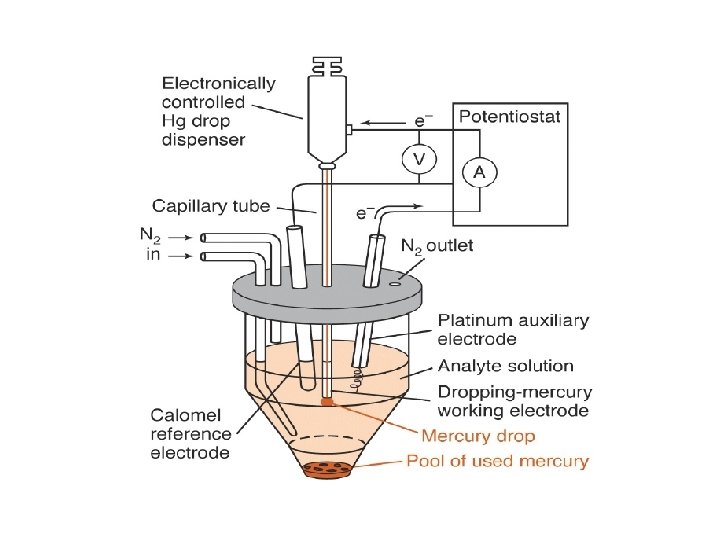
Voltammetry The measurement of variations in current produced by variations of the potential applied to a working electrode polarography: • Heyrovsky (1922): first voltammetry experiments using a dropping mercury working electrode In voltammetry, once the applied potential is sufficiently negative, electron transfer occurs between the electrode and the electroactive species: Cu 2+ + 2 e → Cu(Hg)

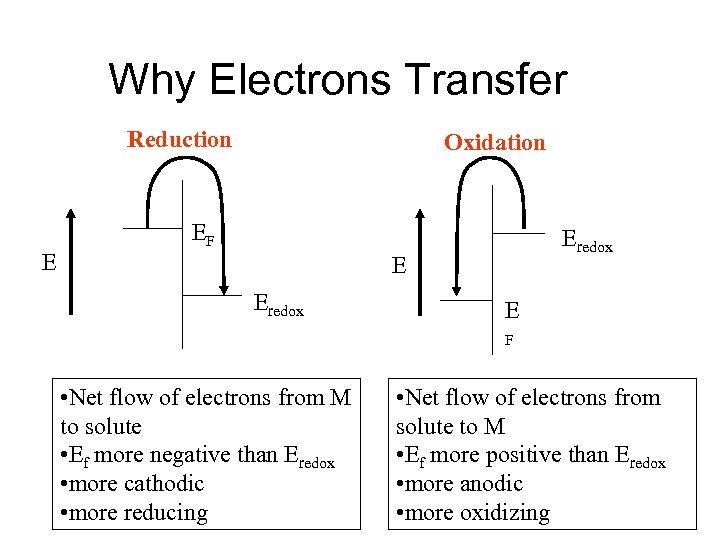Why Electrons Transfer Reduction E Oxidation EF Eredox E F • Net flow of electrons from M to solute • Ef more negative than Eredox • more cathodic • more reducing • Net flow of electrons from solute to M • Ef more positive than Eredox • more anodic • more oxidizing

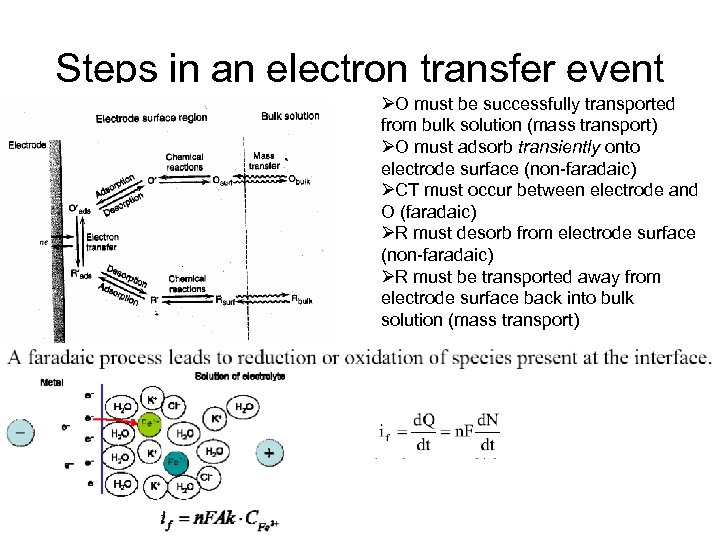Steps in an electron transfer event ØO must be successfully transported from bulk solution (mass transport) ØO must adsorb transiently onto electrode surface (non-faradaic) ØCT must occur between electrode and O (faradaic) ØR must desorb from electrode surface (non-faradaic) ØR must be transported away from electrode surface back into bulk solution (mass transport)

Mass Transport or Mass Transfer • • • Migration – movement of a charged particle in a potential field Diffusion – movement due to a concentration gradient. If electrochemical reaction depletes (or produces) some species at the electrode surface, then a concentration gradient develops and the electroactive species will tend to diffuse from the bulk solution to the electrode (or from the electrode out into the bulk solution) Convection – mass transfer due to stirring. Achieved by some form of mechanical movement of the solution or the electrode i. e. , stir solution, rotate or vibrate electrode Difficult to get perfect reproducibility with stirring, better to move the electrode Convection is considerably more efficient than diffusion or migration = higher currents for a given concentration = greater analytical sensitivity

Nernst-Planck Equation Diffusion Migration Convection Ji(x) = flux of species i at distance x from electrode (mole/cm 2 s) Di = diffusion coefficient (cm 2/s) Ci(x)/ x = concentration gradient at distance x from electrode (x)/ x = potential gradient at distance x from electrode (x) = velocity at which species i moves (cm/s)

Diffusion Fick’s 1 st Law I = n. FAJ Solving Fick’s Laws for particular applications like electrochemistry involves establishing Initial Conditions and Boundary Conditions

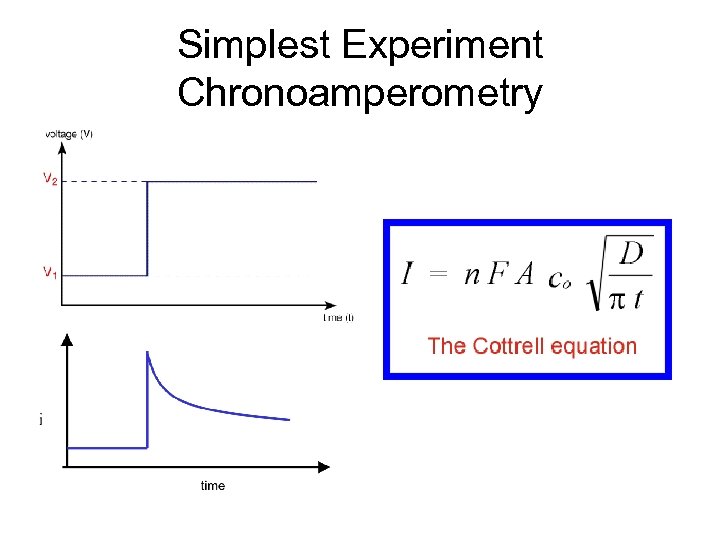Simplest Experiment Chronoamperometry

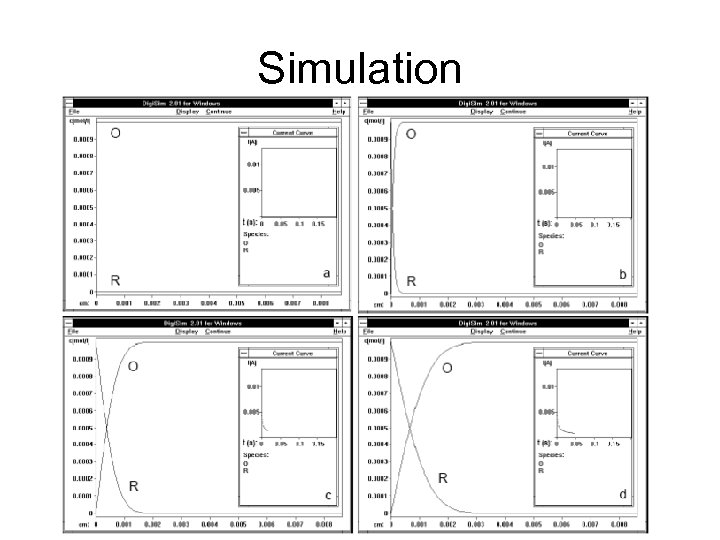Simulation

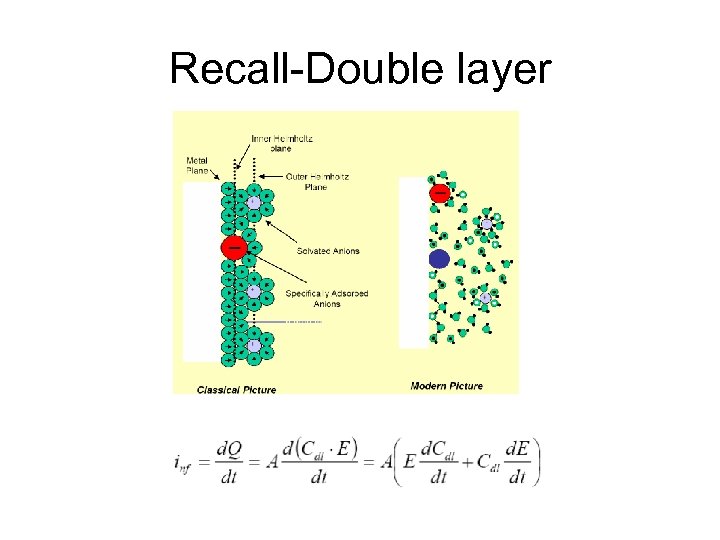Recall-Double layer

Double-Layer charging • Charging/discharging a capacitor upon application of a potential step Itotal = Ic + IF

Working electrode choice • Depends upon potential window desired – Overpotential – Stability of material – Conductivity – contamination

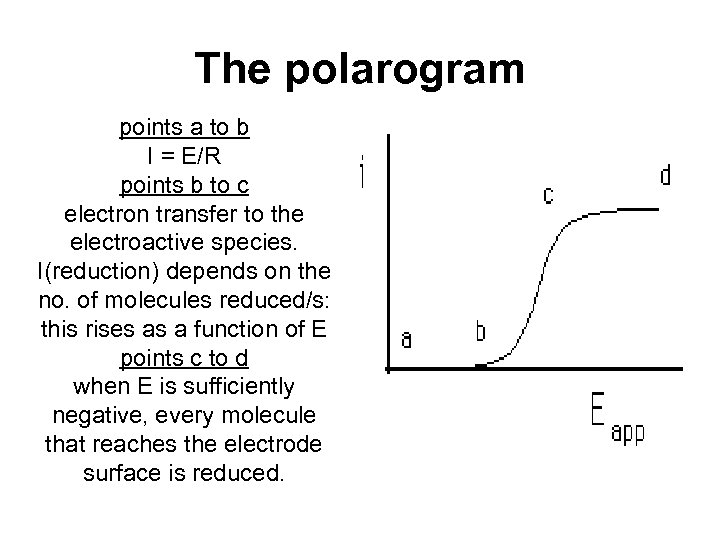The polarogram points a to b I = E/R points b to c electron transfer to the electroactive species. I(reduction) depends on the no. of molecules reduced/s: this rises as a function of E points c to d when E is sufficiently negative, every molecule that reaches the electrode surface is reduced.

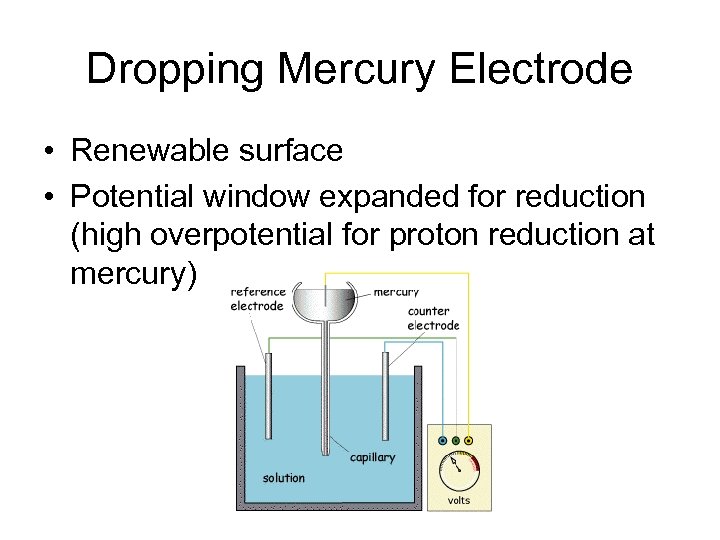Dropping Mercury Electrode • Renewable surface • Potential window expanded for reduction (high overpotential for proton reduction at mercury)

Polarography A = 4 (3 mt/4 d)2/3 = 0. 85(mt)2/3 Density of drop Mass flow rate of drop We can substitute this into Cottrell Equation i(t) = n. FACD 1/2/ 1/2 t 1/2 We also replace D by 7/3 D to account for the compression of the diffusion layer by the expanding drop Giving the Ilkovich Equation: id = 708 n. D 1/2 m 2/3 t 1/6 C I has units of Amps when D is in cm 2 s-1, m is in g/s and t is in seconds. C is in mol/cm 3 This expression gives the current at the end of the drop life. The average current is obtained by integrating the current over this time period iav = 607 n. D 1/2 m 2/3 t 1/6 C

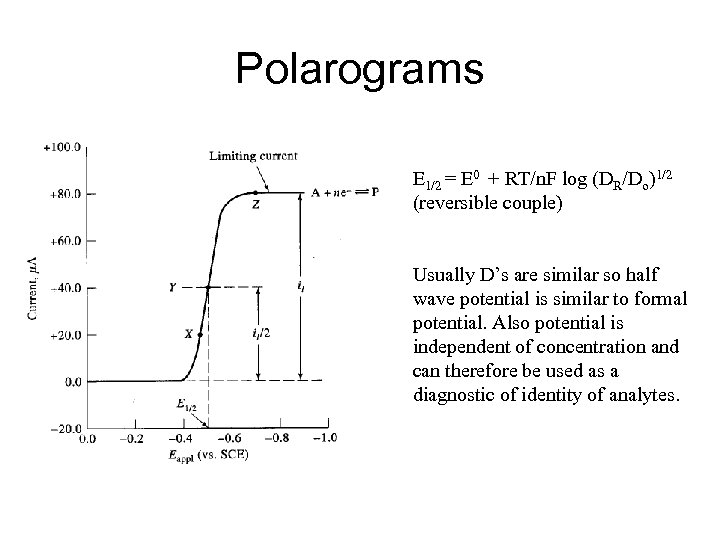Polarograms E 1/2 = E 0 + RT/n. F log (DR/Do)1/2 (reversible couple) Usually D’s are similar so half wave potential is similar to formal potential. Also potential is independent of concentration and can therefore be used as a diagnostic of identity of analytes.

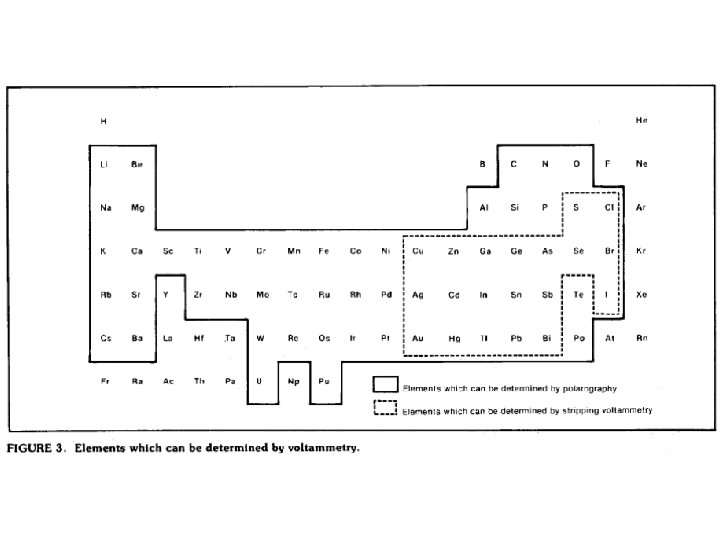
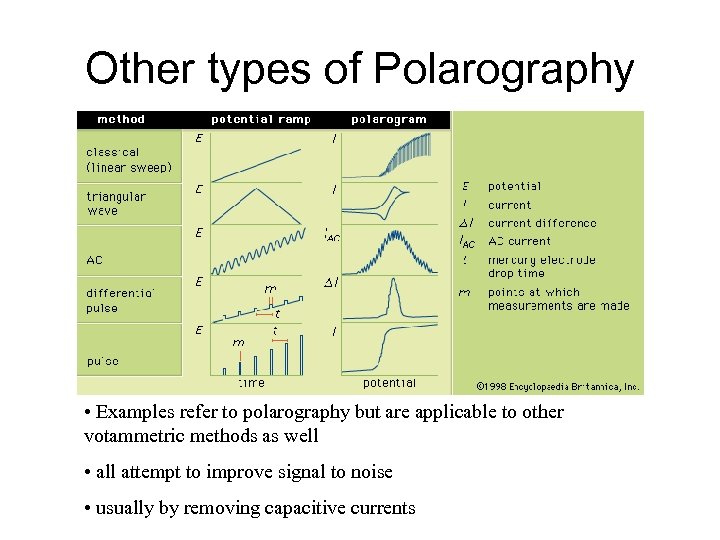Other types of Polarography • Examples refer to polarography but are applicable to other votammetric methods as well • all attempt to improve signal to noise • usually by removing capacitive currents

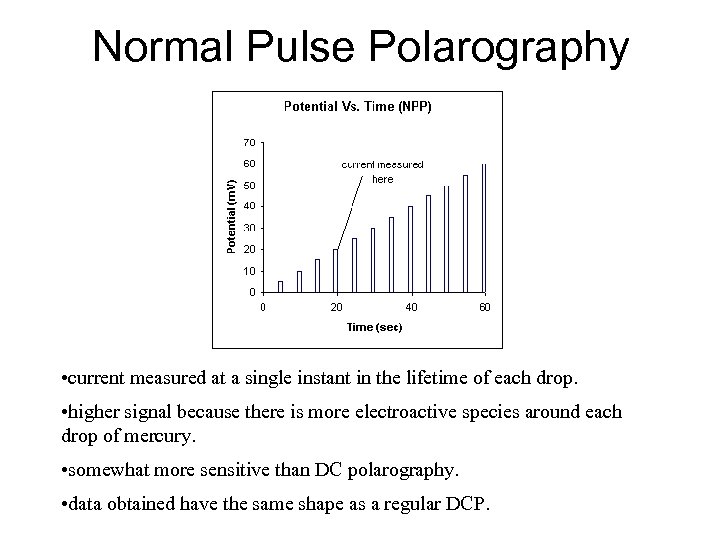Normal Pulse Polarography • current measured at a single instant in the lifetime of each drop. • higher signal because there is more electroactive species around each drop of mercury. • somewhat more sensitive than DC polarography. • data obtained have the same shape as a regular DCP.

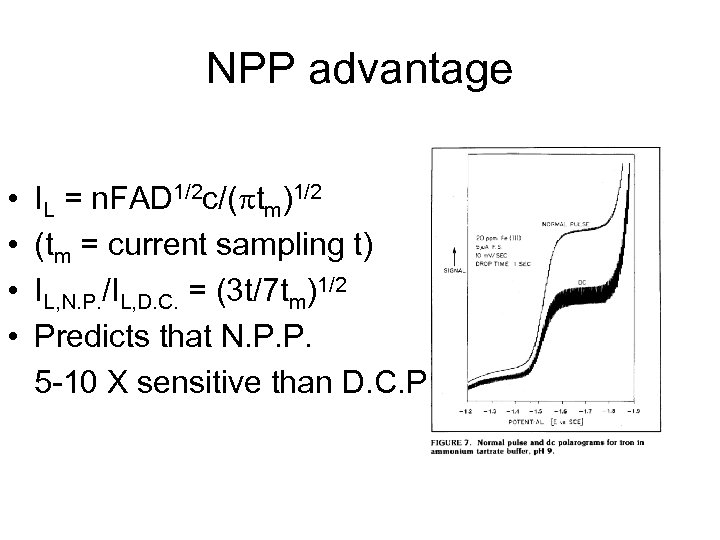NPP advantage • • IL = n. FAD 1/2 c/( tm)1/2 (tm = current sampling t) IL, N. P. /IL, D. C. = (3 t/7 tm)1/2 Predicts that N. P. P. 5 -10 X sensitive than D. C. P.

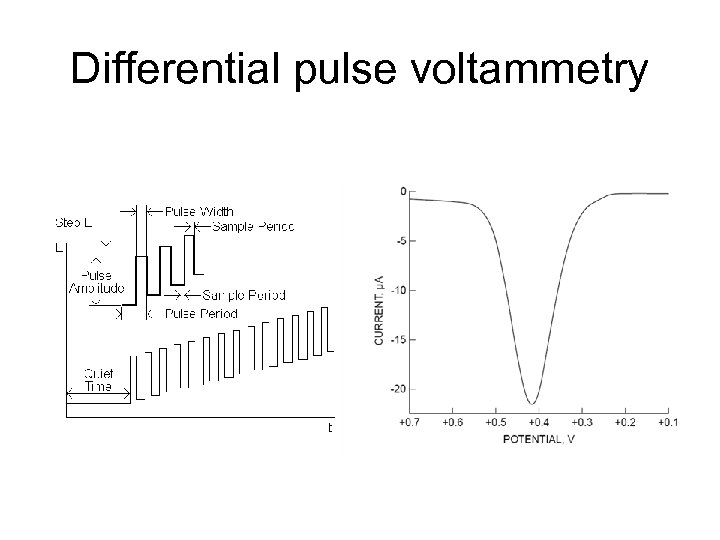Differential pulse voltammetry

DPP • current measured twice during the lifetime of each drop difference in current is plotted. • Results in a peak-shaped feature, where the top of the peak corresponds to E 1/2, and the height gives concentration • This shape is the derivative of the regular DC data. • DPP has the advantage of sensitive detection limits and discrimination against background currents. Traditionally, metals in the ppm range can be determined with DPP. • Derivative improves contrast (resolution) between overlapping waves

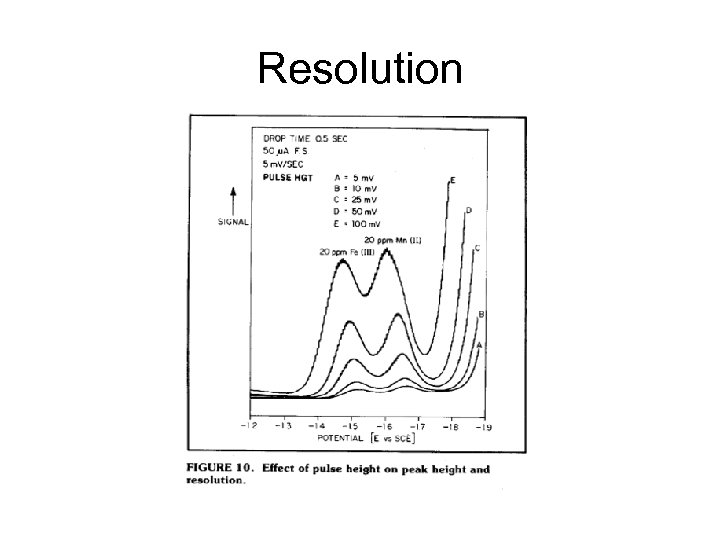
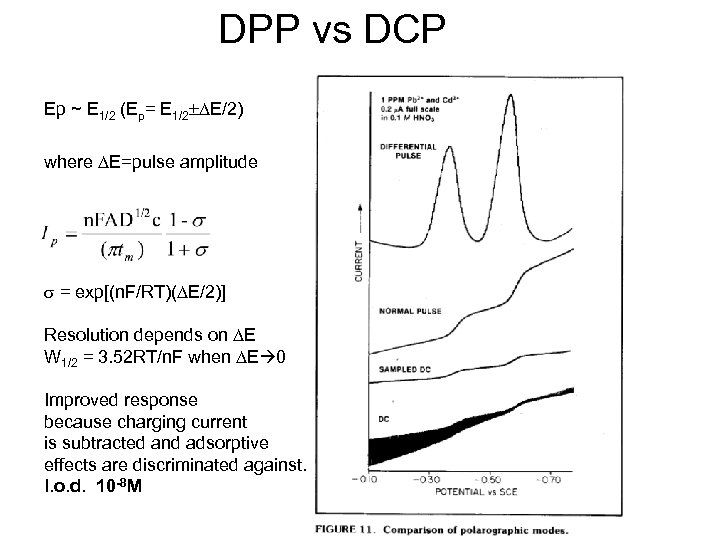DPP vs DCP Ep ~ E 1/2 (Ep= E 1/2±DE/2) where DE=pulse amplitude s = exp[(n. F/RT)(DE/2)] Resolution depends on DE W 1/2 = 3. 52 RT/n. F when DE 0 Improved response because charging current is subtracted and adsorptive effects are discriminated against. l. o. d. 10 -8 M

Resolution

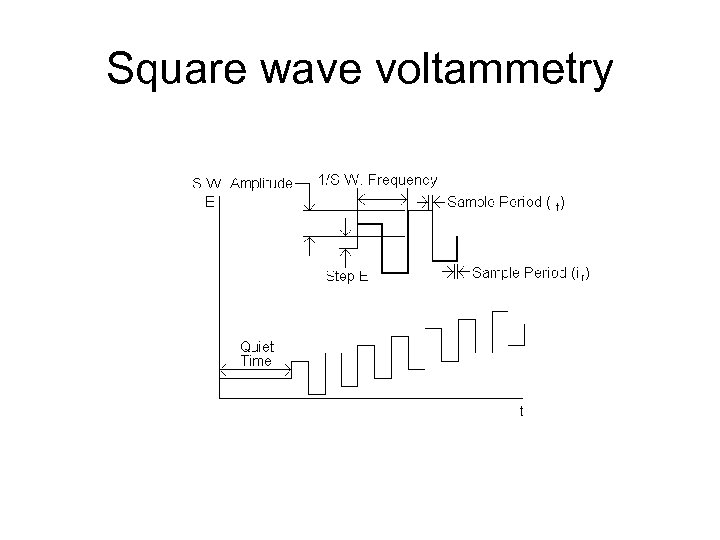Square wave voltammetry

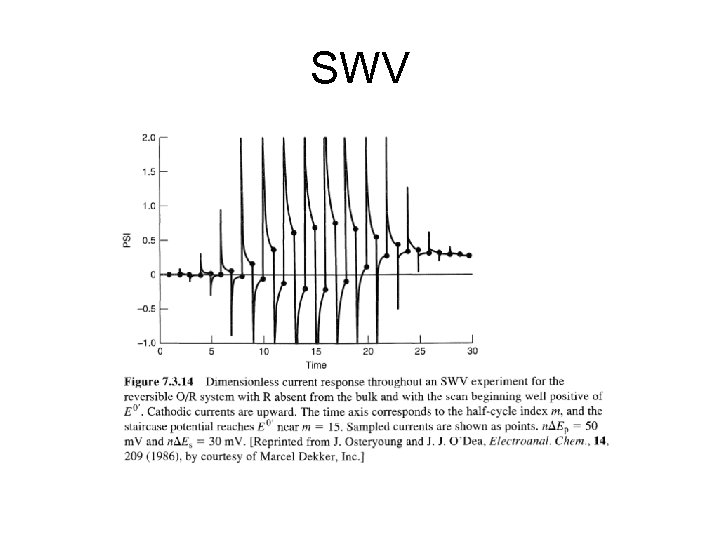SWV

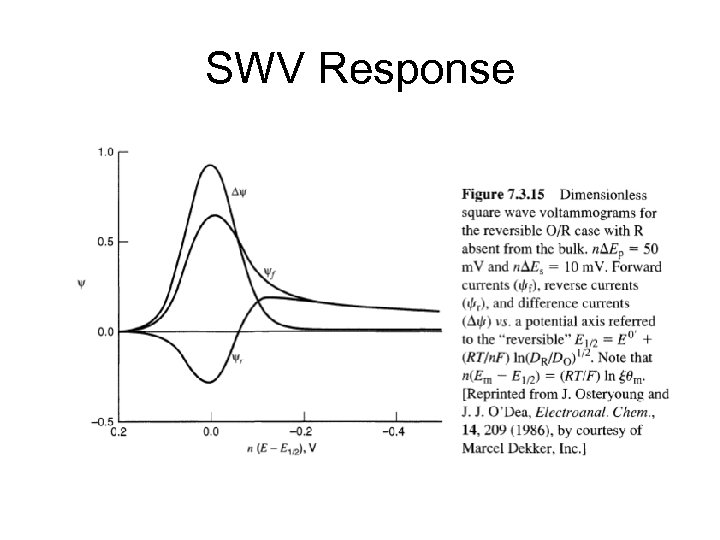SWV Response

SWV • advantage of square wave voltammetry is that the entire scan be performed on a single mercury drop in about 10 seconds, as opposed to about 5 minutes for the techniques described previously. SWV saves time, reduces the amount of mercury used per scan by a factor of 100. If used with a prereduction step, detection limits of 1 -10 ppb can be achieved, which rivals graphite furnace AA in sensitivity. • data for SWV similar to DPP • height and width of the wave depends on the exact combination of experimental parameters (i. e. scan rate and pulse height

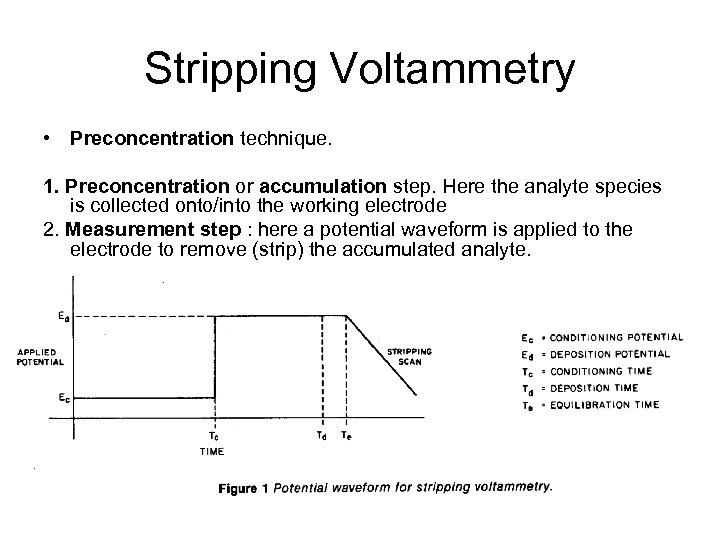Stripping Voltammetry • Preconcentration technique. 1. Preconcentration or accumulation step. Here the analyte species is collected onto/into the working electrode 2. Measurement step : here a potential waveform is applied to the electrode to remove (strip) the accumulated analyte.

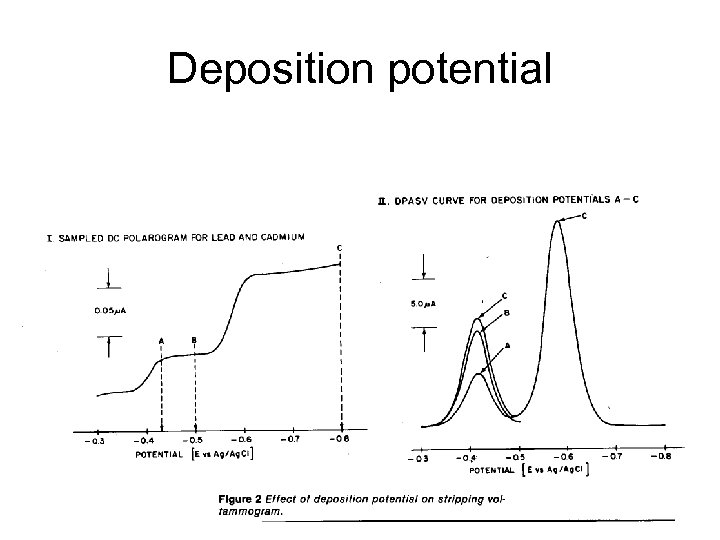Deposition potential

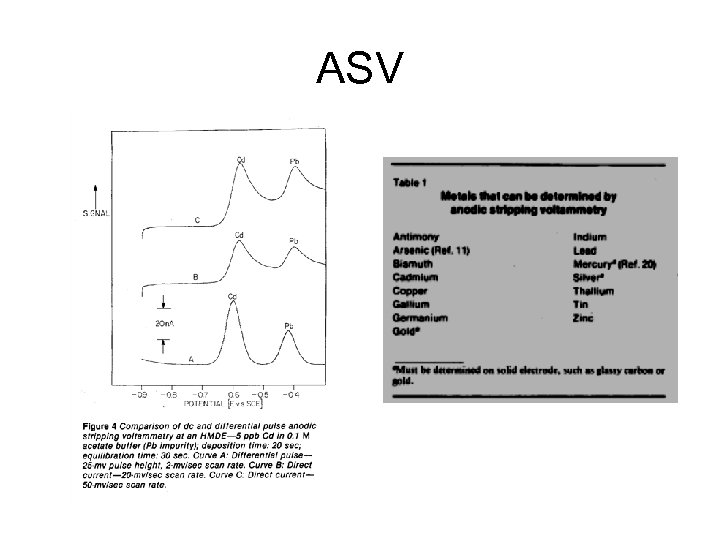ASV

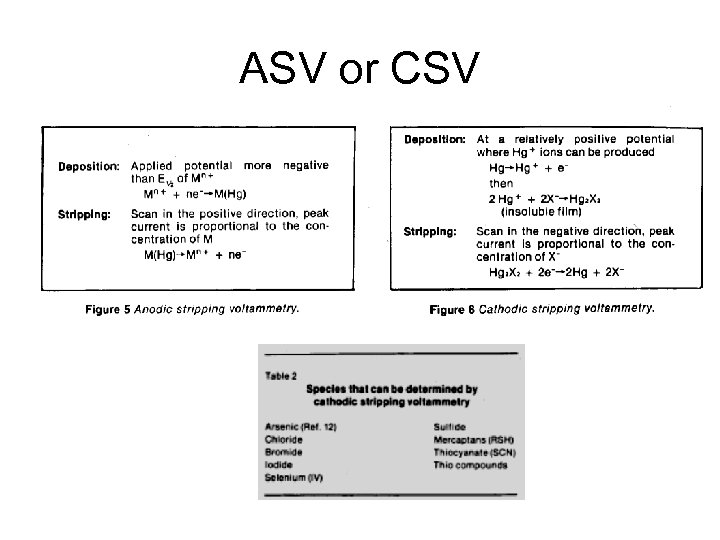ASV or CSV

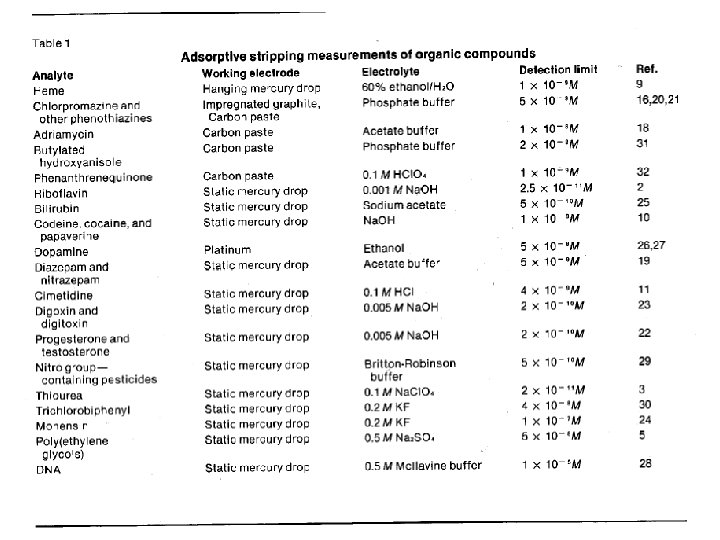
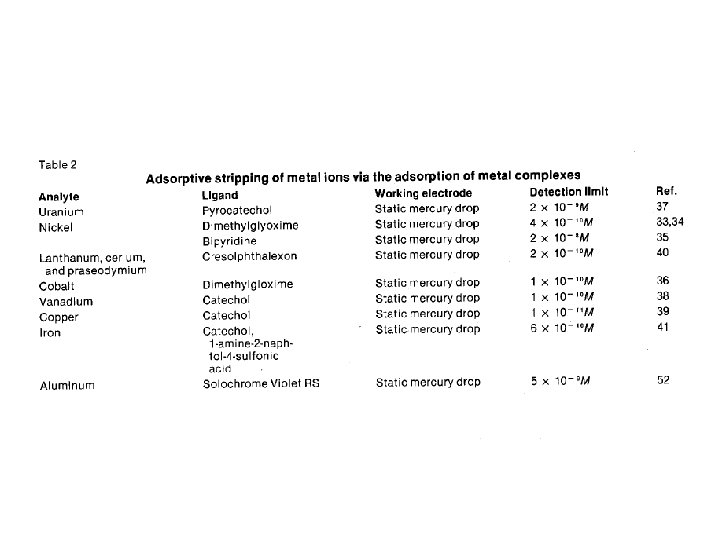
Adsorptive Stripping Voltammetry • Use a chelating ligand that adsorbs to the WE. • Can detect by redox process of metal or ligand.

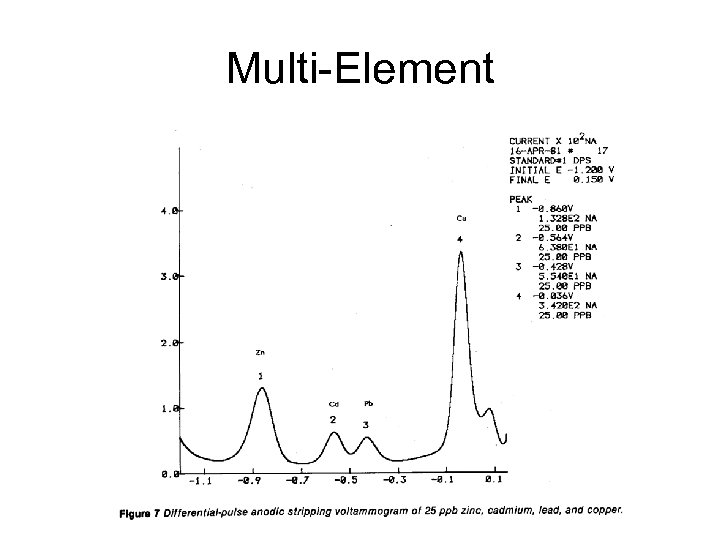Multi-Element

Standard Addition