ELEC 7770 Advanced VLSI Design Spring 2010 Also

ELEC 7770: Advanced VLSI Design Spring 2010 (Also, ELEC 7250 Class on March 11, 2010) Radio Frequency (RF) Testing Vishwani D. Agrawal James J. Danaher Professor ECE Department, Auburn University Auburn, AL 36849 vagrawal@eng. auburn. edu http: //www. eng. auburn. edu/~vagrawal/COURSE/E 7770_Spr 10 Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 1

References 1. S. Bhattacharya and A. Chatterjee, "RF Testing, " Chapter 16, pages 2. 3. 4. 5. 6. 745 -789, in System on Chip Test Architectures, edited by L. -T. Wang, C. E. Stroud and N. A. Touba, Amsterdam: Morgan-Kaufman, 2008. M. L. Bushnell and V. D. Agrawal, Essentials of Electronic Testing for Digital, Memory & Mixed-Signal VLSI Circuits, Boston: Springer, 2000. J. Kelly and M. Engelhardt, Advanced Production Testing of RF, So. C, and Si. P Devices, Boston: Artech House, 2007. B. Razavi, RF Microelectronics, Upper Saddle River, New Jersey: Prentice Hall PTR, 1998. J. Rogers, C. Plett and F. Dai, Integrated Circuit Design for High. Speed Frequency Synthesis, Boston: Artech House, 2006. K. B. Schaub and J. Kelly, Production Testing of RF and System-on-achip Devices for Wireless Communications, Boston: Artech House, 2004. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 2

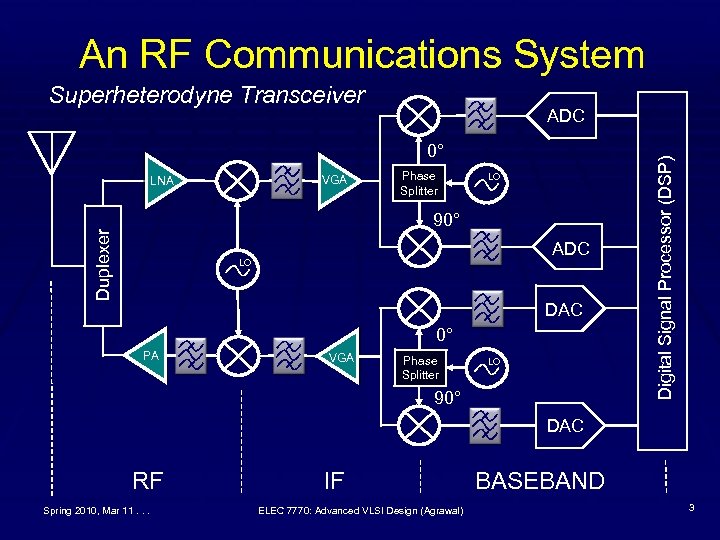An RF Communications System Superheterodyne Transceiver 0° VGA LNA Phase Splitter LO Duplexer 90° ADC LO DAC 0° PA VGA Phase Splitter LO 90° Digital Signal Processor (DSP) ADC DAC RF Spring 2010, Mar 11. . . IF ELEC 7770: Advanced VLSI Design (Agrawal) BASEBAND 3

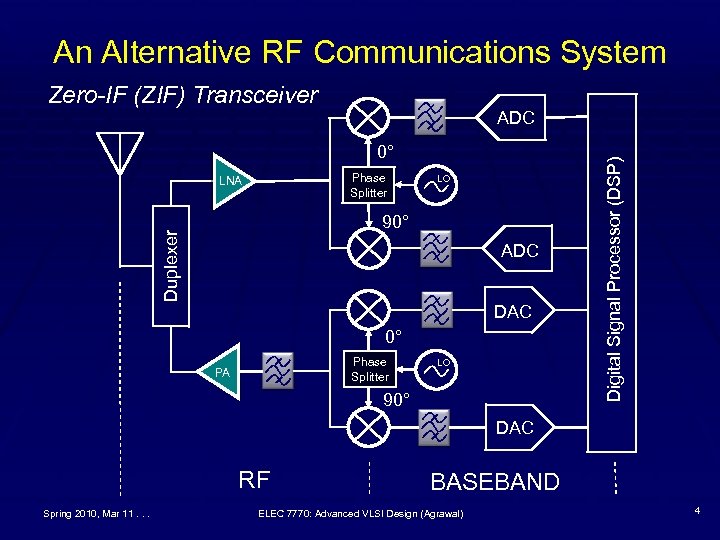An Alternative RF Communications System Zero-IF (ZIF) Transceiver 0° Phase Splitter LNA LO Duplexer 90° ADC DAC 0° Phase Splitter PA LO 90° Digital Signal Processor (DSP) ADC DAC RF Spring 2010, Mar 11. . . BASEBAND ELEC 7770: Advanced VLSI Design (Agrawal) 4

Components of an RF System § Radio frequency § Duplexer § LNA: Low noise amplifier § PA: Power amplifier § RF mixer § Local oscillator § Filter § Mixed-signal § ADC: Analog to digital converter § DAC: Digital to analog converter § Digital signal processor § Intermediate frequency (DSP) § VGA: Variable gain amplifier § Modulator § Demodulator § Filter Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 5

LNA: Low Noise Amplifier § Amplifies received RF signal § Typical characteristics: § Noise figure § IP 3 § Gain § Input and output impedance § Reverse isolation § Stability factor 2 d. B – 10 d. Bm 15 d. B 50Ω 20 d. B >1 § Technologies: § Bipolar § CMOS § Reference: Razavi, Chapter 6. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 6

PA: Power Amplifier § Feeds RF signal to antenna for transmission § Typical characteristics: § § § Output power +20 to +30 d. Bm § Efficiency 30% to 60% § IMD – 30 d. Bc § Supply voltage 3. 8 to 5. 8 V § Gain 20 to 30 d. B § Output harmonics – 50 to – 70 d. Bc § Power control On-off or 1 -d. B steps § Stability factor >1 Technologies: § Ga. As § Si. Ge Reference: Razavi, Chapter 9. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 7

Mixer or Frequency (Up/Down) Converter § Translates frequency by adding or subtracting § local oscillator (LO) frequency Typical characteristics: § Noise figure § IP 3 § Gain § Input impedance § Port to port isolation 12 d. B +5 d. Bm 10 d. B 50Ω 10 -20 d. B § Tecnologies: § Bipolar § MOS § Reference: Razavi, Chapter 6. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 8

LO: Local Oscillator § Provides signal to mixer for down conversion or § upconversion. Implementations: § Tuned feedback amplifier § Ring oscillator § Phase-locked loop (PLL) § Direct digital synthesizer (DDS) Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 9

SOC: System-on-a-Chip § All components of a system are implemented on § § the same VLSI chip. Requires same technology (usually CMOS) used for all components. Components not implemented on present-day SOC: § Antenna § Power amplifier (PA) Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 10

RF Tests § Basic tests § § § Scattering parameters (S-parameters) § Frequency and gain measurements § Power efficiency measurements Distortion measurements Noise measurements Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 11

Scattering Parameters (S-Parameters) § An RF function is a two-port device with § Characteristic impedance (Z 0): § Z 0 = 50Ω for wireless communications devices § Z 0 = 75Ω for cable TV devices § Gain and frequency characteristics § S-Parameters of an RF device § S 11 : input return loss or input reflection coefficient § S 22 : output return loss or output reflection coefficient § S 21 : gain or forward transmission coefficient § S 12 : isolation or reverse transmission coefficient § S-Parameters are complex numbers and can be expressed in decibels as 20 × log | Sij | Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 12

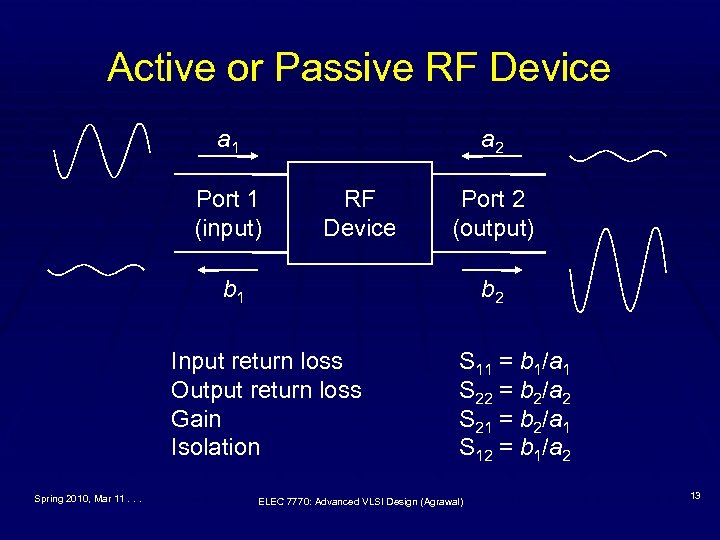Active or Passive RF Device a 1 a 2 Port 1 (input) RF Device Port 2 (output) b 1 b 2 Input return loss Output return loss Gain Isolation Spring 2010, Mar 11. . . S 11 = b 1/a 1 S 22 = b 2/a 2 S 21 = b 2/a 1 S 12 = b 1/a 2 ELEC 7770: Advanced VLSI Design (Agrawal) 13

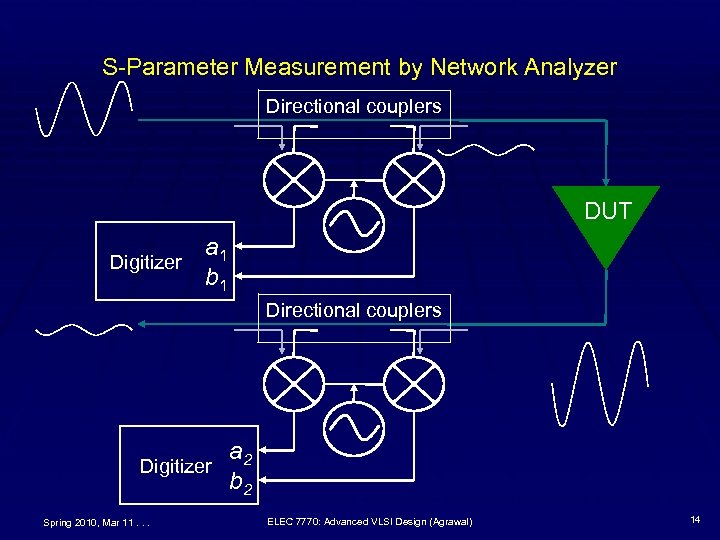S-Parameter Measurement by Network Analyzer Directional couplers DUT a 1 Digitizer b 1 Directional couplers a 2 Digitizer b 2 Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 14

Application of S-Parameter: Input Match § Example: In an S-parameter measurement setup, rms value of input voltage is 0. 1 V and the rms value of the reflected voltage wave is 0. 02 V. Assume that the output of DUT is perfectly matched. Then S 11 determines the input match: § S 11 = 0. 02/0. 1 = 0. 2, or 20 × log (0. 2) = – 14 d. B. § Suppose the required input match is – 10 d. B; this device passes the test. § Similarly, S 22 determines the output match. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 15

Gain (S 21) and Gain Flatness § An amplifier of a Bluetooth transmitter operates over a § § § frequency band 2. 4 – 2. 5 GHz. It is required to have a gain of 20 d. B and a gain flatness of 1 d. B. Test: Under properly matched conditions, S 21 is measured at several frequencies in the range of operation: § S 21 = 15. 31 at 2. 400 GHz § S 21 = 14. 57 at 2. 499 GHz From the measurements: § At 2. 400 GHz, Gain = 20×log 15. 31 = 23. 70 d. B § At 2. 499 GHz, Gain = 20×log 14. 57 = 23. 27 d. B Result: Gain and gain flatness meet specification. Measurements at more frequencies in the range may be useful. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 16

Power Measurements § Receiver § § § Minimum detectable RF power Maximum allowed input power Power levels of interfering tones § Transmitter § § Maximum RF power output Changes in RF power when automatic gain control is used RF power distribution over a frequency band Power-added efficiency (PAE) § Power unit: d. Bm, relative to 1 m. W § § § Power in d. Bm = 10 × log (power in watts/0. 001 watts) Example: 1 W is 10×log 1000 = 30 d. Bm What is 2 W in d. Bm? Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 17

Harmonic Measurements § Multiples of the carrier frequency are called § § harmonics. Harmonics are generated due to nonlinearity in semiconductor devices and clipping (saturation) in amplifiers. Harmonics may interfere with other signals and must be measured to verify that a manufactured device meets the specification. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 18

Power-Added Efficiency (PAE) § Definition: Power-added efficiency of an RF amplifier is § § § the ratio of RF power generated by the amplifier to the DC power supplied: § PAE = ΔPRF / PDC where § ΔPRF = PRF(output) – PRF(input) § Pdc = Vsupply × Isupply Important for power amplifier (PA). 1 – PAE is a measure of heat generated in the amplifier, i. e. , the battery power that is wasted. In mobile phones PA consumes most of the power. A low PAE reduces the usable time before battery recharge. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 19

PAE Example § Following measurements are obtained for an RF § power amplifier: § RF Input power = +2 d. Bm § RF output power = +34 d. Bm § DC supply voltage = 3 V § DUT current = 2. 25 A PAE is calculated as follows: § PRF(input) = 0. 001 × 102/10 = 0. 0015 W § PRF(output) = 0. 001 × 1034/10 = 2. 5118 W § Pdc = 3× 2. 25 = 6. 75 W § PAE = (2. 5118 – 0. 00158)/6. 75 = 0. 373 or 37. 2% Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 20

Distortion and Linearity § An unwanted change in the signal behavior is § § usually referred to as distortion. The cause of distortion is nonlinearity of semiconductor devices constructed with diodes and transistors. Linearity: § Function f(x) = ax + b, although a straight-line is not § referred to as a linear function. Definition: A linear function must satisfy: § f(x + y) = f(x) + f(y), and § f(ax) = a f(x), for all scalar constants a Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 21

Linear and Nonlinear Functions f(x) slope = a b b x x f(x) = ax + b f(x) = ax 2 + b f(x) slope = a x f(x) = ax Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 22

Generalized Transfer Function § Transfer function of an electronic circuit is, in § general, a nonlinear function. Can be represented as a polynomial: § vo = a 0 + a 1 vi + a 2 vi 2 + a 3 vi 3 + · · § Constant term a 0 is the dc component that in RF § circuits is usually removed by a capacitor or highpass filter. For a linear circuit, a 2 = a 3 = · · = 0. Electronic vi Spring 2010, Mar 11. . . circuit ELEC 7770: Advanced VLSI Design (Agrawal) vo 23

Effect of Nonlinearity on Frequency § § Consider a transfer function, vo = a 0 + a 1 vi + a 2 vi 2 + a 3 vi 3 Let vi = A cos ωt Using the identities (ω = 2πf): § cos 2 ωt = (1 + cos 2ωt)/2 § cos 3 ωt = (3 cos ωt + cos 3ωt)/4 We get, § vo Spring 2010, Mar 11. . . = a 0 + a 2 A 2/2 + (a 1 A + 3 a 3 A 3/4) cos ωt + (a 2 A 2/2) cos 2ωt + (a 3 A 3/4) cos 3ωt ELEC 7770: Advanced VLSI Design (Agrawal) 24

Problem for Solution § A diode characteristic is, I = Is ( eαV – 1) § Where, V = V 0 + vin, V 0 is dc voltage and vin is small signal ac § voltage. Is is saturation current and α is a constant that depends on temperature and design parameters of diode. Using the Taylor series expansion, express the diode current I as a polynomial in vin. I 0 V – Is Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 25

Linear and Nonlinear Circuits and Systems § Linear devices: § All frequencies in the output of a device are related to § input by a proportionality, or weighting factor, independent of power level. § No frequency will appear in the output, that was not present in the input. Nonlinear devices: § A true linear device is an idealization. Most electronic devices are nonlinear. § Nonlinearity in amplifier is undesirable and causes distortion of signal. § Nonlinearity in mixer or frequency converter is essential. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 26

Types of Distortion and Their Tests § Types of distortion: § Harmonic distortion: single-tone test § Gain compression: single-tone test § Intermodulation distortion: two-tone or multitone test § Testing procedure: Output spectrum measurement Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 27

Harmonic Distortion § Harmonic distortion is the presence of multiples of a § § fundamental frequency of interest. N times the fundamental frequency is called Nth harmonic. Disadvantages: § Waste of power in harmonics. § Interference from harmonics. Measurement: § Single-frequency input signal applied. § Amplitudes of the fundamental and harmonic frequencies are analyzed to quantify distortion as: § Total harmonic distortion (THD) § Signal, noise and distortion (SINAD) Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 28

Problem for Solution § Show that for a nonlinear device with a single frequency input of amplitude A, the nth harmonic component in the output always contains a term proportional to An. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 29

Total Harmonic Distortion (THD) § THD is the total power contained in all harmonics of a § § signal expressed as percentage (or ratio) of the fundamental signal power. THD(%) = [(P 2 + P 3 + · · · ) / Pfundamental ] × 100% Or THD(%) = [(V 22 + V 32 + · · · ) / V 2 fundamental ] × 100% § Where P 2, P 3, . . . , are the power in watts of second, third, . . . , § harmonics, respectively, and Pfundamental is the fundamental signal power, And V 2, V 3, . . . , are voltage amplitudes of second, third, . . . , harmonics, respectively, and Vfundamental is the fundamental signal amplitude. § Also, THD(d. B) = 10 log THD(%) § For an ideal distortionless signal, THD = 0% or – ∞ d. B Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 30

THD Measurement § THD is specified typically for devices with RF § § output. Separate power measurements are made for the fundamental and each harmonic. THD is tested at specified power level because § THD may be small at low power levels. § Harmonics appear when the output power of an RF device is raised. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 31

Gain Compression § The harmonics produced due to nonlinearity in an § § amplifier reduce the fundamental frequency power output (and gain). This is known as gain compression. As input power increases, so does nonlinearity causing greater gain compression. A standard measure of Gain compression is “ 1 -d. B compression point” power level P 1 d. B, which can be § Input referred for receiver, or § Output referred for transmitter Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 32

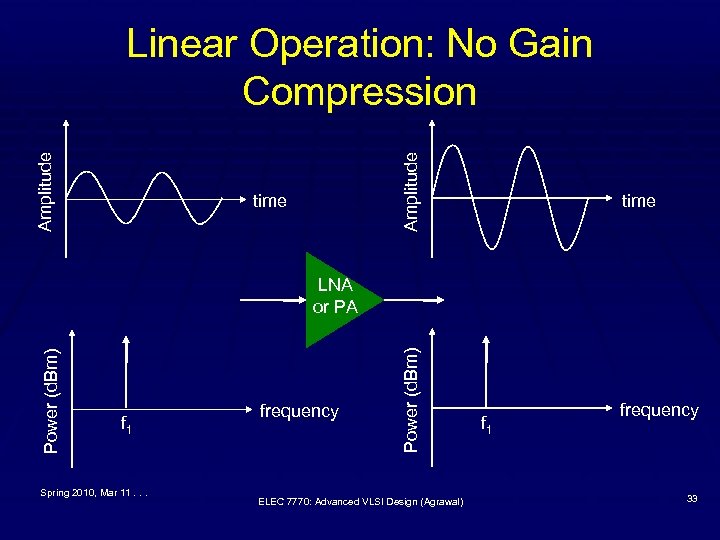Amplitude Linear Operation: No Gain Compression time f 1 Spring 2010, Mar 11. . . frequency Power (d. Bm) LNA or PA ELEC 7770: Advanced VLSI Design (Agrawal) f 1 frequency 33

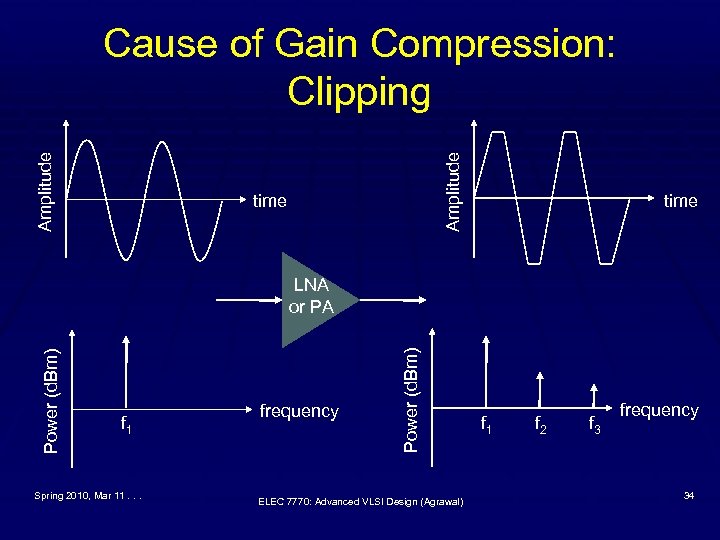Amplitude Cause of Gain Compression: Clipping time f 1 Spring 2010, Mar 11. . . frequency Power (d. Bm) LNA or PA ELEC 7770: Advanced VLSI Design (Agrawal) f 1 f 2 f 3 frequency 34

Effect of Nonlinearity § Assume a transfer function, vo = a 0 + a 1 vi + a 2 vi 2 § Let vi = A cos ωt § Using the identities (ω = 2πf): § + a 3 v i 3 § cos 2 ωt = (1 + cos 2ωt)/2 § cos 3 ωt = (3 cos ωt + cos 3ωt)/4 We get, § vo = a 0 + a 2 A 2/2 + (a 1 A + 3 a 3 A 3/4) cos ωt + (a 2 A 2/2) cos 2ωt + (a 3 A 3/4) cos 3ωt Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 35

Gain Compression Analysis § DC term is filtered out. § For small-signal input, A is small § § § A 2 and A 3 terms are neglected § vo = a 1 A cos ωt, small-signal gain, G 0 = a 1 Gain at 1 -d. B compression point, G 1 d. B = G 0 – 1 Input referred and output referred 1 -d. B power: P 1 d. B(output) – P 1 d. B(input) = G 1 d. B = G 0 – 1 Spring 2010, Mar 11. . . 36 ELEC 7770: Advanced VLSI Design (Agrawal)

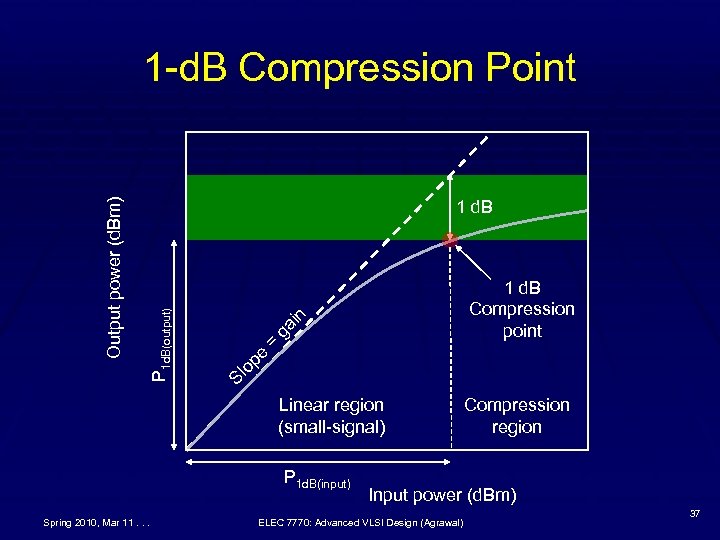1 d. B op e = ga i n 1 d. B Compression point Sl P 1 d. B(output) Output power (d. Bm) 1 -d. B Compression Point Linear region (small-signal) P 1 d. B(input) Spring 2010, Mar 11. . . Compression region Input power (d. Bm) ELEC 7770: Advanced VLSI Design (Agrawal) 37

Testing for Gain Compression § Apply a single-tone input signal: 1. Measure the gain at a power level where DUT is linear. 2. Extrapolate the linear behavior to higher power levels. 3. Increase input power in steps, measure the gain and compare to extrapolated values. 4. Test is complete when the gain difference between steps 2 and 3 is 1 d. B. § Alternative test: After step 2, conduct a binary search for 1 -d. B compression point. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 38

Example: Gain Compression Test § Small-signal gain, G 0 = 28 d. B § Input-referred 1 -d. B compression point power level, § P 1 d. B(input) = – 19 d. Bm We compute: § 1 -d. B compression point Gain, G 1 d. B = 28 – 1 = 27 d. B § Output-referred 1 -d. B compression point power level, P 1 d. B(output) Spring 2010, Mar 11. . . = = = P 1 d. B(input) + G 1 d. B – 19 + 27 8 d. Bm ELEC 7770: Advanced VLSI Design (Agrawal) 39

Intermodulation Distortion § Intermodulation distortion is relevant to devices that handle § § § multiple frequencies. Consider an input signal with two frequencies ω1 and ω2: vi = A cos ω1 t + B cos ω2 t Nonlinearity in the device function is represented by vo = a 0 + a 1 vi + a 2 vi 2 + a 3 vi 3, neglecting higher order terms Therefore, device output is vo = a 0 + a 1 (A cos ω1 t + B cos ω2 t) DC and fundamental + a 2 (A cos ω1 t + B cos ω2 t)2 2 nd order terms + a 3 (A cos ω1 t + B cos ω2 t)3 3 rd order terms Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 40

Problems to Solve § Derive the following: vo = a 0 + a 1 (A cos ω1 t + B cos ω2 t) + a 2 [ A 2 (1+cos 2ω1 t)/2 + AB cos (ω1+ω2)t + AB cos (ω1 – ω2)t + B 2 (1+cos 2ω2 t)/2 ] + a 3 (A cos ω1 t + B cos ω2 t)3 § Hint: Use the identity: § cos α cos β = [cos(α + β) + cos(α – β)] / 2 § Simplify a 3 (A cos ω1 t + B cos ω2 t)3 Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 41

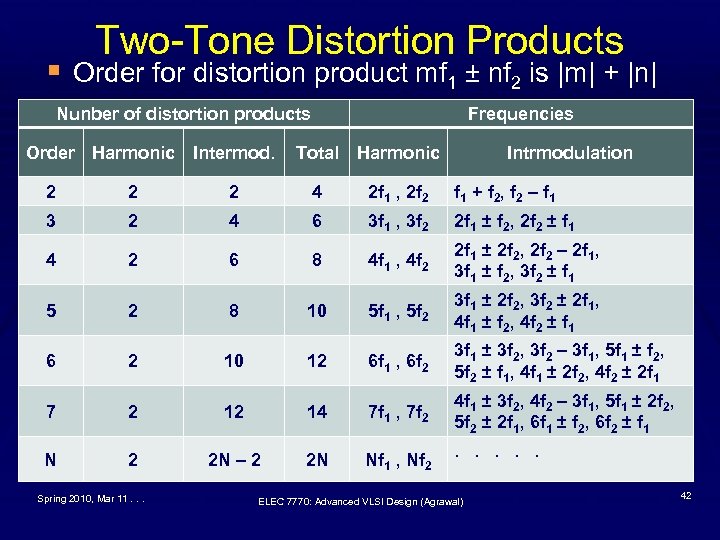Two-Tone Distortion Products § Order for distortion product mf 1 ± nf 2 is |m| + |n| Nunber of distortion products Order Harmonic Frequencies Intermod. Total Harmonic Intrmodulation 2 2 2 4 2 f 1 , 2 f 2 f 1 + f 2 , f 2 – f 1 3 2 4 6 3 f 1 , 3 f 2 2 f 1 ± f 2, 2 f 2 ± f 1 4 2 6 8 4 f 1 , 4 f 2 2 f 1 ± 2 f 2, 2 f 2 – 2 f 1, 3 f 1 ± f 2, 3 f 2 ± f 1 5 2 8 10 5 f 1 , 5 f 2 3 f 1 ± 2 f 2, 3 f 2 ± 2 f 1, 4 f 1 ± f 2, 4 f 2 ± f 1 6 2 10 12 6 f 1 , 6 f 2 3 f 1 ± 3 f 2, 3 f 2 – 3 f 1, 5 f 1 ± f 2, 5 f 2 ± f 1, 4 f 1 ± 2 f 2, 4 f 2 ± 2 f 1 7 2 12 14 7 f 1 , 7 f 2 4 f 1 ± 3 f 2, 4 f 2 – 3 f 1, 5 f 1 ± 2 f 2, 5 f 2 ± 2 f 1, 6 f 1 ± f 2, 6 f 2 ± f 1 N 2 2 N – 2 2 N Nf 1 , Nf 2 Spring 2010, Mar 11. . . . ELEC 7770: Advanced VLSI Design (Agrawal) 42

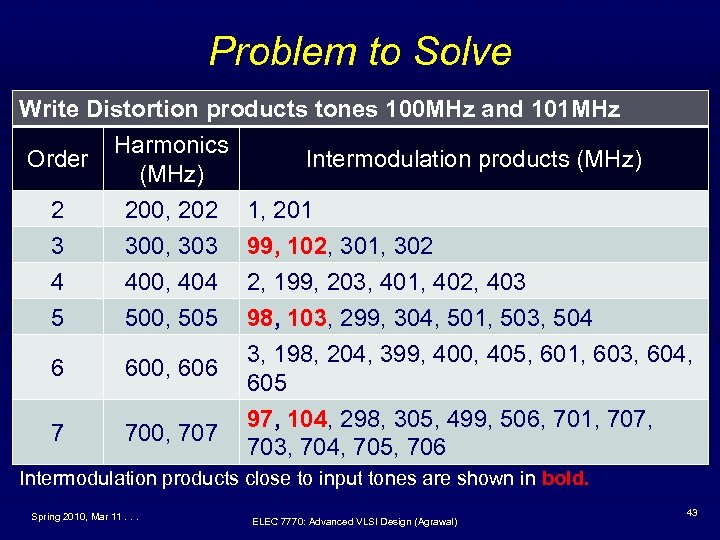Problem to Solve Write Distortion products tones 100 MHz and 101 MHz Harmonics Order Intermodulation products (MHz) 2 200, 202 1, 201 3 4 5 300, 303 400, 404 500, 505 6 600, 606 99, 102, 301, 302 2, 199, 203, 401, 402, 403 98, 103, 299, 304, 501, 503, 504 3, 198, 204, 399, 400, 405, 601, 603, 604, 605 7 700, 707 97, 104, 298, 305, 499, 506, 701, 707, 703, 704, 705, 706 Intermodulation products close to input tones are shown in bold. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 43

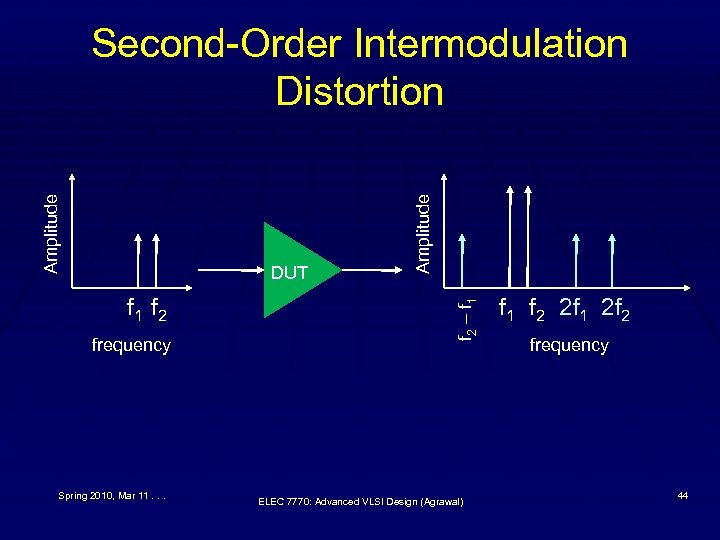f 1 f 2 frequency Spring 2010, Mar 11. . . f 2 – f 1 DUT Amplitude Second-Order Intermodulation Distortion ELEC 7770: Advanced VLSI Design (Agrawal) f 1 f 2 2 f 1 2 f 2 frequency 44

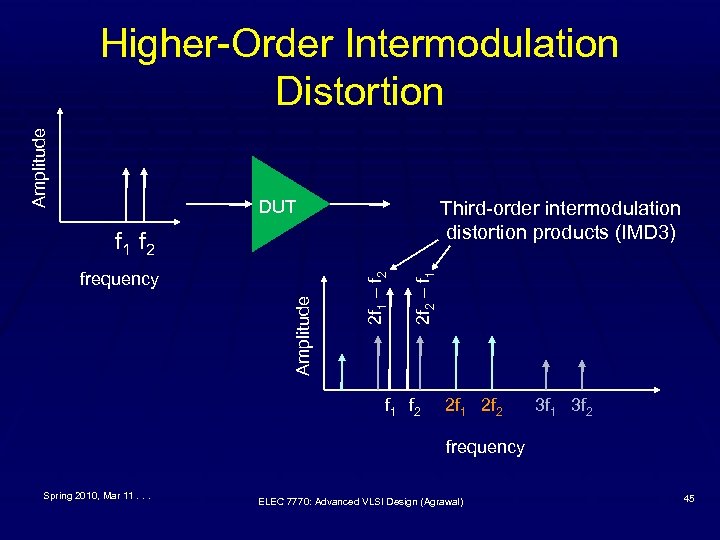Amplitude Higher-Order Intermodulation Distortion DUT Third-order intermodulation distortion products (IMD 3) 2 f 2 – f 1 Amplitude frequency 2 f 1 – f 2 f 1 f 2 2 f 1 2 f 2 3 f 1 3 f 2 frequency Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 45

Problem to Solve § For A = B, i. e. , for two input tones of equal magnitudes, show that: § Output amplitude of each fundamental frequency, f 1 or f 2 , is § 9 a 1 A + — a 3 A 3 ≈ a 1 A 4 Output amplitude of each third-order intermodulation frequency, 2 f 1 – f 2 or 2 f 2 – f 1 , is 3 — a 3 A 3 4 Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 46

Third-Order Intercept Point (IP 3) § IP 3 is the power level of the fundamental for which the § § output of each fundamental frequency equals the output of the closest third-order intermodulation frequency. IP 3 is a figure of merit that quantifies the third-order intermodulation distortion. Assuming a 1 >> 9 a 3 A 2 /4, IP 3 is given by IP 3 = [4 a 1 /(3 a 3 )]1/2 Output a 1 IP 3 = 3 a 3 IP 33 / 4 a 1 A 3 a 3 A 3 / 4 IP 3 Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) A 47

Test for IP 3 § Select two test frequencies, f 1 and f 2, applied in equal § § magnitude to the input of DUT. Increase input power P 0 (d. Bm) until the third-order products are well above the noise floor. Measure output power P 1 in d. Bm at any fundamental frequency and P 3 in d. Bm at a third-order intermodulation frquency. Output-referenced IP 3: OIP 3 = P 1 + (P 1 – P 3) / 2 Input-referenced IP 3: IIP 3 = P 0 + (P 1 – P 3) / 2 = OIP 3 – G Because, Gain for fundamental frequency, G = P 1 – P 0 Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 48

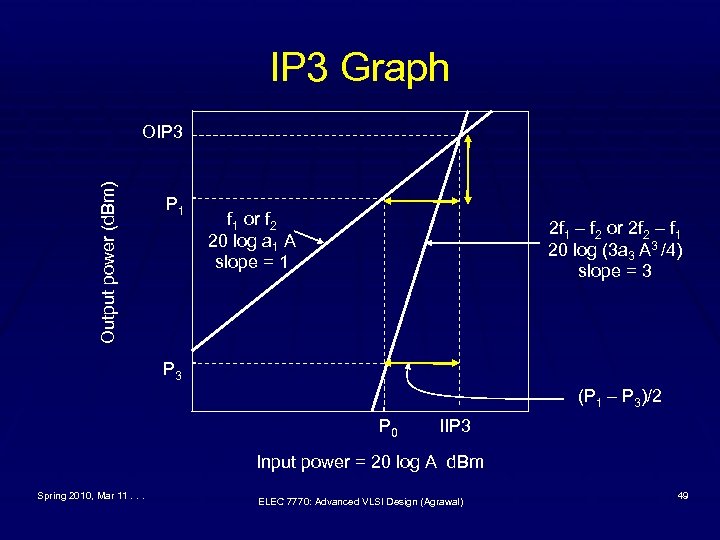IP 3 Graph Output power (d. Bm) OIP 3 P 1 f 1 or f 2 20 log a 1 A slope = 1 2 f 1 – f 2 or 2 f 2 – f 1 20 log (3 a 3 A 3 /4) slope = 3 P 3 (P 1 – P 3)/2 P 0 IIP 3 Input power = 20 log A d. Bm Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 49

Example: IP 3 of an RF LNA § § § Gain of LNA = 20 d. B RF signal frequencies: 2140. 10 MHz and 2140. 30 MHz Second-order intermodulation distortion: 400 MHz; outside operational band of LNA. Third-order intermodulation distortion: 2140. 50 MHz; within the operational band of LNA. Test: § § § Input power, P 0 = – 30 d. Bm, for each fundamental frequency Output power, P 1 = – 30 + 20 = – 10 d. Bm Measured third-order intermodulation distortion power, P 3 = – 84 d. Bm OIP 3 = – 10 + [( – 10 – ( – 84))] / 2 = + 27 d. Bm IIP 3 = – 10 + [( – 10 – ( – 84))] / 2 – 20 = + 7 d. Bm Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 50

What is Noise? § Noise in an RF system is unwanted random fluctuations in a desired § § § signal. Noise is a natural phenomenon and is always present in the environment. Effects of noise: § Interferes with detection of signal (hides the signal). § Causes errors in information transmission by changing signal. § Sometimes noise might imitate a signal falsely. All communications system design and operation must account for noise. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 51

Describing Noise § Consider noise as a random voltage or current § § function, x(t), over interval – T/2 < t < T/2. Fourier transform of x(t) is XT(f). Power spectral density (PSD) of noise is power across 1Ω Sx(f) = lim [ E{ |XT(f)|2 } / (2 T) ] volts 2/Hz T→∞ This is also expressed in d. Bm/Hz. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 52

Thermal Noise § Thermal (Johnson) noise: Caused by random movement § § of electrons due to thermal energy that is proportional to temperature. Called white noise due to uniform PSD over all frequencies. Mean square open circuit noise voltage across R Ω resistor [Nyquist, 1928]: v 2 = 4 hf. BR / [exp(hf/k. T) – 1] § Where § Plank’s constant h = 6. 626 × 1034 J-sec § Frequency and bandwidth in hertz = f, B § Boltzmann’s constant k = 1. 38 × 10 – 23 J/K § Absolute temperature in Kelvin = T 53 Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal)

Problem to Solve § Given that for microwave frequencies, hf << k. T, derive § the following Rayleigh-Jeans approximation: v 2 = 4 k. TBR Show that at room temperature (T = 290 K), thermal noise power supplied by resistor R to a matched load is kt. B or – 174 d. Bm/Hz. Noisy resistor R R Matched load v = (4 k. TBR)1/2 Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 54

Other Noise Types § Shot noise [Schottky, 1928]: Broadband noise due to random § § behavior of charge carriers in semiconductor devices. Flicker (1/f) noise: Low-frequency noise in semiconductor devices, perhaps due to material defects; power spectrum falls off as 1/f. Can be significant at audio frequencies. Quantization noise: Caused by conversion of continuous valued analog signal to discrete-valued digital signal; minimized by using more digital bits. Quantum noise: Broadband noise caused by the quantized nature of charge carriers; significant at very low temperatures (~0 K) or very high bandwidth ( > 1015 Hz). Plasma noise: Caused by random motion of charges in ionized medium, possibly resulting from sparking in electrical contacts; generally, not a concern. Spring 2010, Mar 11. . . 55 ELEC 7770: Advanced VLSI Design (Agrawal)

Measuring Noise § Expressed as noise power density in the units of d. Bm/Hz. § Noise sources: § Resistor at constant temperature, noise power = k. TB W/Hz. § Avalanche diode § Noise temperature: § Tn = (Available noise power in watts)/(k. B) kelvins § Excess noise ratio (ENR) is the difference in the noise output between hot (on) and cold (off) states, normalized to reference thermal noise at room temperature (290 K): § ENR = [k( Th – Tc )B]/(k. T 0 B) = ( Th / T 0) – 1 § Where noise output in cold state is takes same as reference. § 10 log ENR ~ 15 to 20 d. B Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 56

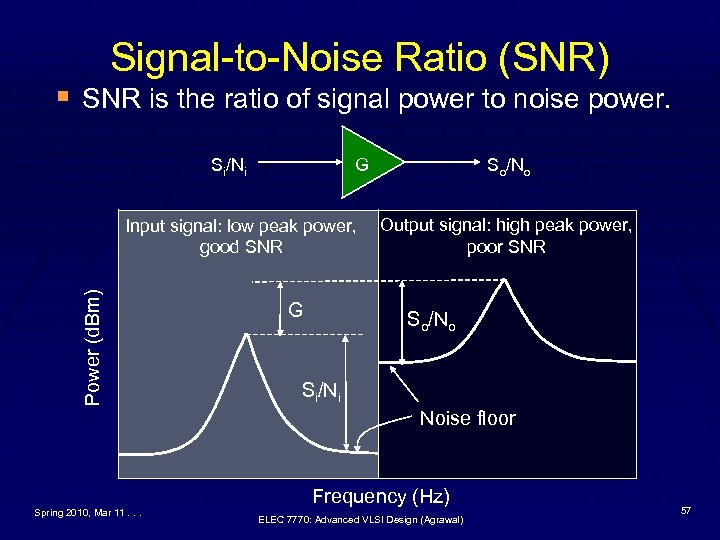Signal-to-Noise Ratio (SNR) § SNR is the ratio of signal power to noise power. Si/Ni G Power (d. Bm) Input signal: low peak power, good SNR G So/No Output signal: high peak power, poor SNR So/No Si/Ni Noise floor Spring 2010, Mar 11. . . Frequency (Hz) ELEC 7770: Advanced VLSI Design (Agrawal) 57

Noise Factor and Noise Figure § Noise factor (F) is the ratio of input SNR to output SNR: § F = (Si /Ni) / (So /No) § = No / ( GNi ), when Si = 1 W and G = gain of DUT = No /( k. T 0 BG), when Ni = k. T 0 B for input noise source § F≥ 1 Noise figure (NF) is noise factor expressed in d. B: § NF = 10 log F d. B § 0 ≤ NF ≤ ∞ Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 58

Cascaded System Noise Factor § Friis equation [Proc. IRE, July 1944, pp. 419 – 422]: Fsys = F 1 Gain = G 1 Noise factor = F 1 Spring 2010, Mar 11. . . F 2 – 1 + ——— G 1 + Gain = G 2 Noise factor = F 2 F 3 – 1 Fn – 1 ——— + · · + ——————— G 1 G 2 · · · G n – 1 Gain = G 3 Noise factor = F 3 ELEC 7770: Advanced VLSI Design (Agrawal) Gain = Gn Noise factor = Fn 59

Measuring Noise Figure: Cold Noise Method § Example: SOC receiver with large gain so noise output is § § measurable; noise power should be above noise floor of measuring equipment. Gain G is known or previously measured. Noise factor, F = No / (k. T 0 BG), where § No is measured output noise power (noise floor) § B is measurement bandwidth § At 290 K, k. T 0 = – 174 d. Bm/Hz Noise figure, NF = 10 log F = No (d. B) – ( – 174 d. Bm/Hz) – B(d. B) – G(d. B) This measurement is also done using S-parameters. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 60

Y – Factor § Y – factor is the ratio of output noise in hot (power on) state to that in cold (power off) state. § Y = Nh / N c = Nh / N 0 § Y is a simple ratio. § Consider, Nh = k. Th. BG and Nc = k. T 0 BG § Then Nh – Nc = k. BG( Th – T 0 ) or k. BG = ( Nh – Nc ) / ( Th – T 0 ) § Noise factor, F = Nh /( k. T 0 BG) = ( Nh / T 0 ) [ 1 / (k. BG) ] = ( Nh / T 0 ) ( Th – T 0 ) / (Nh – Nc ) = ENR / (Y – 1) Spring 2010, Mar 11. . . 61 ELEC 7770: Advanced VLSI Design (Agrawal)

Measuring Noise Factor: Y – Factor Method § Noise source provides hot and cold noise power levels and is § § § characterized by ENR (excess noise ratio). Tester measures noise power, is characterized by its noise factor F 2 and Y-factor Y 2. Device under test (DUT) has gain G 1 and noise factor F 1. Two-step measurement: § Calibration: Connect noise source to tester, measure output power for hot and cold noise inputs, compute Y 2 and F 2. § Measurement: Connect noise source to DUT and tester cascade, measure output power for hot and cold noise inputs, compute Y 12, F 12 and G 1. § Use Friis equation to obtain F 1. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 62

Calibration Noise source ENR Tester (power meter) F 2 , Y 2 § Y 2 = Nh 2 / Nc 2, where § § Nh 2 = measured power for hot source § Nc 2 = measured power for cold source F 2 = ENR / (Y 2 – 1) Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 63

Cascaded System Measurement Noise source ENR Tester (power meter) F 2 , Y 2 DUT F 1 , Y 1 , G 1 F 12, Y 12 § Y 12 = Nh 12 / Nc 12, where § § § Nh 12 = measured power for hot source § Nc 12 = measured power for cold source F 12 = ENR / ( Y 12 – 1 ) G 1 = ( Nh 12 – Nc 12 ) / ( Nh 2 – Nc 2 ) Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 64

Problem to Solve § Show that from noise measurements on a cascaded system, the noise factor of DUT is given by F 2 – 1 F 1 = F 12 – ——— G 1 Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 65

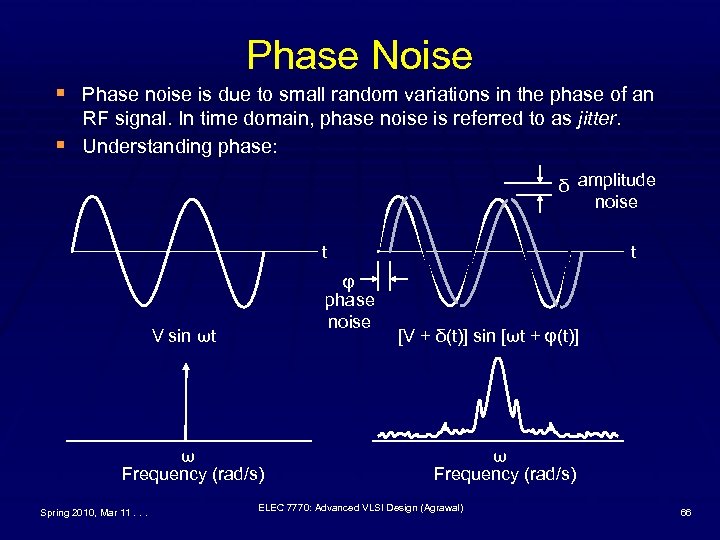Phase Noise § Phase noise is due to small random variations in the phase of an § RF signal. In time domain, phase noise is referred to as jitter. Understanding phase: δ amplitude noise t φ phase noise V sin ωt ω Frequency (rad/s) Spring 2010, Mar 11. . . t [V + δ(t)] sin [ωt + φ(t)] ω Frequency (rad/s) ELEC 7770: Advanced VLSI Design (Agrawal) 66

Effects of Phase Noise § Similar to phase modulation by a random signal. § Two types: § Long term phase variation is called frequency drift. § Short term phase variation is phase noise. § Definition: Phase noise is the Fourier spectrum (power spectral density) of a sinusoidal carrier signal with respect to the carrier power. L(f) = Pn /Pc (as ratio) = Pn in d. Bm/Hz – Pc in d. Bm (as d. Bc) § Pn is RMS noise power in 1 -Hz bandwidth at frequency f § Pc is RMS power of the carrier Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 67

Phase Noise Analysis [V + δ(t)] sin [ωt + φ(t)] = [V + δ(t)] [sin ωt cos φ(t) + cos ωt sin φ(t)] ≈ [V + δ(t)] sin ωt + [V + δ(t)] φ(t) cos ωt In-phase carrier frequency with amplitude noise White noise δ(t) corresponds to noise floor Quadrature-phase carrier frequency with amplitude and phase noise Short-term phase noise corresponds to phase noise spectrum Phase spectrum, L(f) = Sφ(f)/2 Where Sφ(f) is power spectrum of φ(t) Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 68

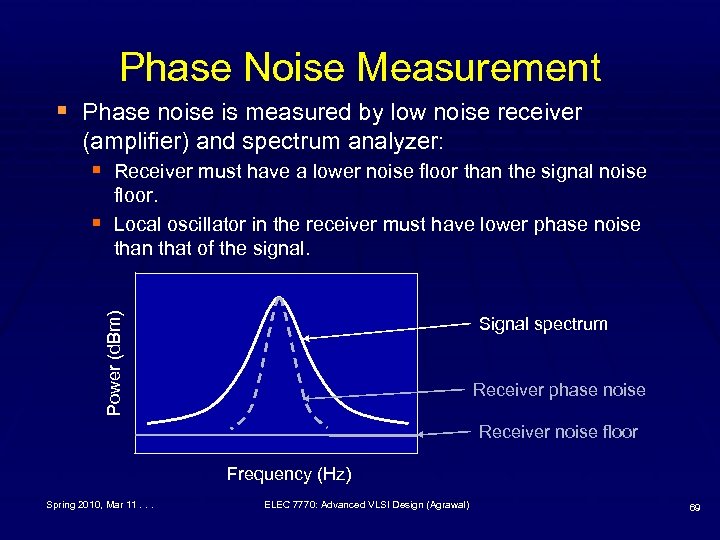Phase Noise Measurement § Phase noise is measured by low noise receiver (amplifier) and spectrum analyzer: § Receiver must have a lower noise floor than the signal noise Power (d. Bm) § floor. Local oscillator in the receiver must have lower phase noise than that of the signal. Signal spectrum Receiver phase noise Receiver noise floor Frequency (Hz) Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 69

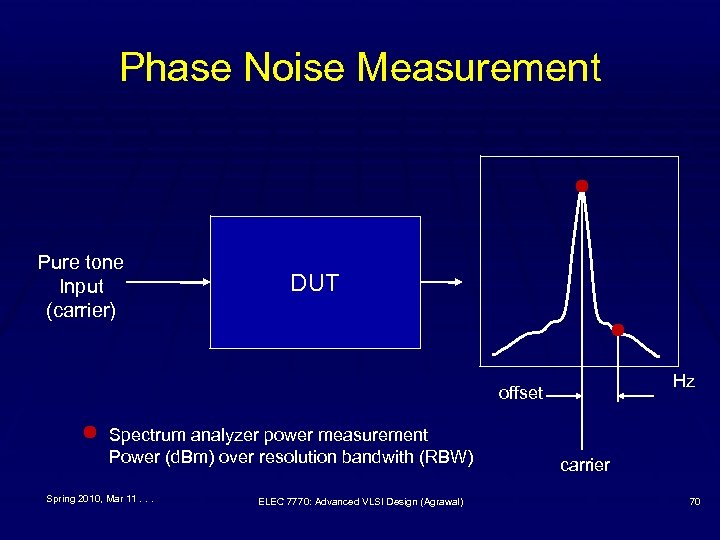Phase Noise Measurement Pure tone Input (carrier) DUT Hz offset Spectrum analyzer power measurement Power (d. Bm) over resolution bandwith (RBW) Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) carrier 70

Phase Noise Measurement Example § Spectrum analyzer data: § RBW = 100 Hz § Frequency offset = 2 k. Hz § Pcarrier = – 5. 30 d. Bm § Poffset = – 73. 16 d. Bm § Phase noise, L(f) = Poffset – Pcarrier – 10 log RBW § = – 73. 16 – ( – 5. 30) – 10 log 100 = – 87. 86 d. Bc/Hz Phase noise is specified as “ – 87. 86 d. Bc/Hz at 2 k. Hz from the carrier. ” Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 71

Problem to Solve § Consider the following spectrum analyzer data: § RBW = 10 Hz § Frequency offset = 2 k. Hz § Pcarrier = – 3. 31 d. Bm § Poffset = – 81. 17 d. Bm § Determine phase noise in d. Bc/Hz at 2 k. Hz from the carrier. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 72

References, Again 1. S. Bhattacharya and A. Chatterjee, "RF Testing, " Chapter 16, pages 2. 3. 4. 5. 6. 745 -789, in System on Chip Test Architectures, edited by L. -T. Wang, C. E. Stroud and N. A. Touba, Amsterdam: Morgan-Kaufman, 2008. M. L. Bushnell and V. D. Agrawal, Essentials of Electronic Testing for Digital, Memory & Mixed-Signal VLSI Circuits, Boston: Springer, 2000. J. Kelly and M. Engelhardt, Advanced Production Testing of RF, So. C, and Si. P Devices, Boston: Artech House, 2007. B. Razavi, RF Microelectronics, Upper Saddle River, New Jersey: Prentice Hall PTR, 1998. J. Rogers, C. Plett and F. Dai, Integrated Circuit Design for High-Speed Frequency Synthesis, Boston: Artech House, 2006. K. B. Schaub and J. Kelly, Production Testing of RF and System-on-a. Chip Devices for Wireless Communications, Boston: Artech House, 2004. Spring 2010, Mar 11. . . ELEC 7770: Advanced VLSI Design (Agrawal) 73