92091c4e18f45dff7092dd4655fcd245.ppt
- Количество слайдов: 16

Экстерналии: продолжение üРешение проблемы экстерналий: аналитический пример üЭкстерналии и асимметричная информация üСетевые экстерналии

Методы решения проблемы экстерналий Аналитический пример: Издержки фирм S и F описываются дифференцируемыми функциями c. S(s, x) и c. F(f, x) со следующими свойствами: То есть, фирма S создает отрицательную экстерналию для фирмы F.

Децентрализованное равновесие Если фирмы S и F действуют независимо, и являются ценополучателями на своих рынках сбыта, они решают следующие задачи: Условия первого порядка: Для фирмы S: Для фирмы F:

Интернализация экстерналии путем объединения фирм Предположим, фирмы S и F принадлежат единому холдингу, который заинтересован в максимизации их суммарной прибыли: Условия первого порядка: Последнее условие: положительный эффект загрязнений (снижение издержек производства стали) должен равняться отрицательному (росту издержек производства рыбы).

Интернализация путем введения налога Пигу Государство вводит налог t на каждую тонну загрязнений. Задача фирмы S: Условия первого порядка: Если установить фирма S будет производить в точности Паретооптимальный объем загрязнений!

Нейтрализация экстерналии путем создания рынка переуступаемых квот Предположим, право на чистую воду закрепляется за фирмой F, и она может продавать фирме S право на некоторый объем загрязнений x по цене q. Задачи фирм принимают вид:

Нейтрализация экстерналии путем создания рынка квот (продолжение) При равновесии на рынке загрязнений мы имеем равенство: Т. е. , значения s* и f*, как и предыдущих методах интернализации, Парето-оптимальны. Мы исходили из того, что изначальное право на чистую воду имеет фирма F. Однако для создания рынка вовсе не обязательно распределять права собственности именно так!

Рынок квот с альтернативным распределением прав собственности Определим права собственности иначе: пусть фирма S имеет право безнаказанно загрязнять реку до некоторого объема. Если она хочет загрязнять больше, она должна заплатить за это фирме F. И наоборот, фирма F может заплатить S за снижение загрязнений, по некоторой цене q. Задача фирмы S: Задача фирмы F: FOC для внутренних решений: При внутренних решениях (т. е. , если торговля загрязнениями вообще происходит), объем загрязнений Парето-оптимален!

Экстерналии и асимметрия информации Почему перечисленные только что способы интернализации экстерналий могут не сработать (и временами не срабатывают)? ПРИМЕР: Пусть производство фирмы связано с отрицательной экстерналией для потребителя, и: h – уровень экстерналии, Φ(h, η) – ущерб потребителя от экстерналии, η – тип потребителя Π(h, θ) – прибыль фирмы от экстерналии, θ – тип фирмы Каждый потребитель и фирма знают свой собственный тип, но о чужих типах знают только то, что η и θ распределены некоторым образом Φ(h, η) и Π(h, θ) – вогнутые функции

Децентрализованное равновесие Ради простоты, пусть возможно только два уровня h: 0 и h. Попробуем создать рынок: наделим потребителей правом на отсутствие экстерналии, и позволим им торговаться с фирмами в режиме «соглашайся или уходи» • • • b(θ) > 0 - выгода фирмы типа θ от экстерналии. c(η) > 0 - потери потребителя типа η от экстерналии. G(b), F(c) – функции распределения b и с (g(b) и f(c) – плотности соответствующих распределений) Заметим, в любом Парето оптимальном распределении, фирмам нужно позволить создавать экстерналии, если b > c! • T – сумма, которую потребитель запросит с фирмы за экстерналию (если b > T, фирма согласится заплатить; вероятность этого события равна 1 – G(T)) • Если потребитель нейтрален к риску, он подберет T так, чтобы максимизировать свою ожидаемую выгоду: max(1 – G(T))(T – c) Решением будет T* > c – и в этом источник неэффективности: обязательно найдутся фирмы, для которых T* > b > c… Можно показать, что и квоты, и налоги тут также не сработают.

Квотирование в условиях асимметричной информации • Φ(h, η) + Π(h, θ) – общественные выгоды от экстерналии в размере h • h*(η, θ) – уровень h, максимизирующий выигрыш общества • hmax – квота на производство экстерналии, установленная так, чтобы максимизировать выигрыш общества при ηa, θa (средних значениях η, θ). Задача фирмы: h* зависит от распределения η и θ, а hmax нет: возможна неэффективность!
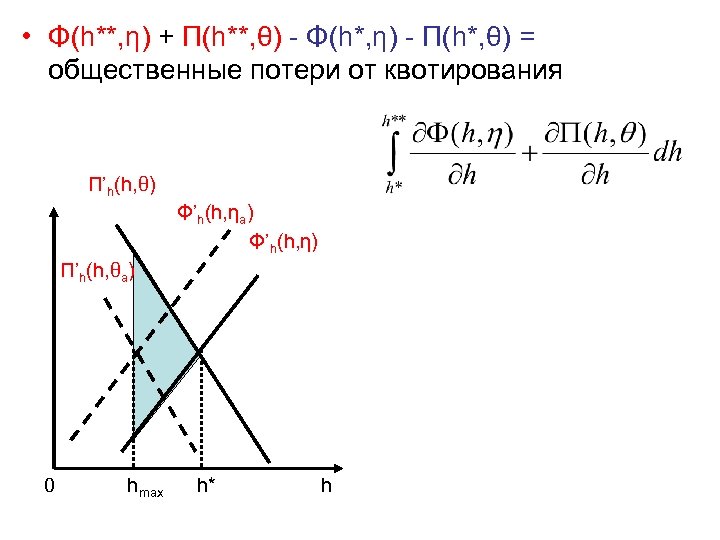
• Φ(h**, η) + Π(h**, θ) - Φ(h*, η) - Π(h*, θ) = общественные потери от квотирования Π’h(h, θ) Φ’h(h, ηa) Φ’h(h, η) Π’h(h, θa) 0 hmax h* h

Налоги Пигу в условиях асимметричной информации Задача фирмы: Налог целесообразно установить на уровне t = Φ’h(h*, ηa) • Φ(ht, η) + Π(ht, θ) - Φ(h*, η) - Π(h*, θ) = общественные потери при налогообложении

Сетевые эффекты Для ряда товаров и услуг, чем больше число пользователей, тем больше выгода каждого. Модель: Рынок товара x (без сетевых экстерналий): • 1000 потребителей, каждый готов купить одну единицу товара x по максимальной цене v = 1… 1000. • проранжируем потребителей так, чтобы номер каждого потребителя соответствовал его резервной цене, v. • если цена товара составляет p, то объем спроса на него составит QD = 1000 – p => получаем стандартную убывающую кривую спроса.

Рынок товара x (с сетевыми экстерналиями): • пусть полезность блага для потребителя v равна vn, где n – общее число потребителей блага. Чем больше людей потребляет благо, тем больше каждый из них готов за него заплатить. Как будет выглядеть спрос на такой товар? • Предположим, технология производства товара характеризуется постоянной отдачей от масштаба, и он продается по цене p. • Рассмотрим потребителя , безразличного между покупкой товара и отказом от него. Его максимальная готовность платить должна быть равна цене товара: Заметим: все потребители, оценивающие товар выше, чем обязательно его купят! Таким образом, равновесие определяется следующим уравнением: p = n(1000 – n)
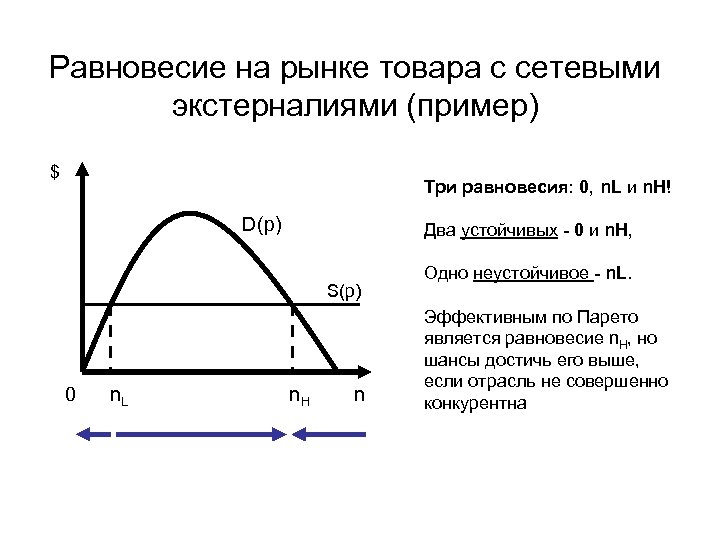
Равновесие на рынке товара с сетевыми экстерналиями (пример) $ Три равновесия: 0, n. L и n. H! D(p) Два устойчивых - 0 и n. H, S(p) 0 n. L n. H n Одно неустойчивое - n. L. Эффективным по Парето является равновесие n. H, но шансы достичь его выше, если отрасль не совершенно конкурентна
92091c4e18f45dff7092dd4655fcd245.ppt