83b159234451ab77c601a07ac2e78f96.ppt
- Количество слайдов: 78

Экспертиза банков тестовых заданий

НЕОБХОДИМОСТЬ ЭКСПЕРТИЗЫ И СЕРТИФИКАЦИИ Концепция модернизации Российского образования Обеспечение современного качества образования Создание условий для повышения уровня качества образования Проблема оценки уровня качества образования Методы дидактического тестирования, БТМ СЕРТИФИКАЦИЯ ТМ

ЗАДАЧИ СЕРТИФИКАЦИИ ТЕСТОВЫХ МАТЕРИАЛОВ 1. Повышение качества ТМ 2. Повышение надежности тестов и уменьшение погрешности тестовых измерений 3. Подтверждение соответствия тестовых материалов методологическим требованиям 4. Стандартизация банков тестовых материалов
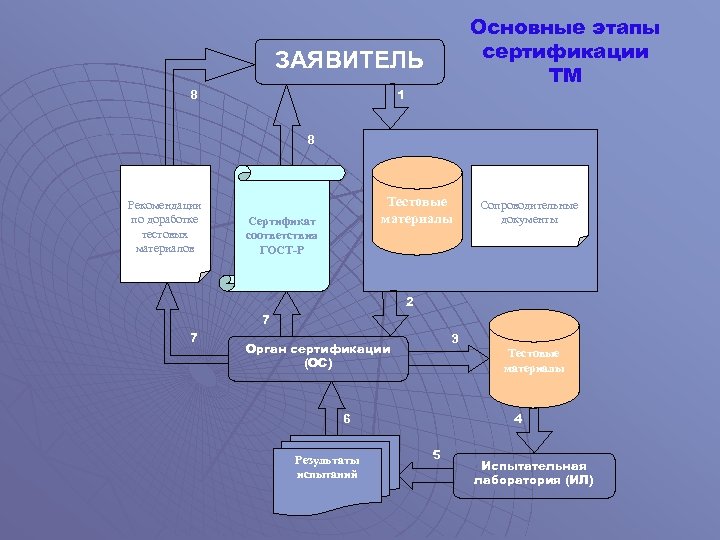
Основные этапы сертификации ТМ ЗАЯВИТЕЛЬ 8 1 8 Рекомендации по доработке тестовых материалов Тестовые материалы Сертификат соответствия ГОСТ-Р Сопроводительные документы 2 7 7 3 Орган сертификации (ОС) 6 Результаты испытаний Тестовые материалы 4 5 Испытательная лаборатория (ИЛ)

ЭТАПЫ СОЗДАНИЯ БТЗ 1 ВЫБОР РЕЗУЛЬТАТА ПРОВЕРКИ 2 СТРУКТУРИЗАЦИЯ УЧЕБНОГО МАТЕРИАЛА 3 СПЕЦИФИКАЦИЯ ТЕСТОВЫХ ЗАДАНИЙ 4 РАЗРАБОТКА КОМПОЗИЦИИ ТЕСТА 5 ОЦЕНКА ВАЛИДНОСТИ ТЕСТА

ЭТАПЫ СОЗДАНИЯ БТЗ 6 ЭКСПЕРТИЗА БТЗ И ЗАДАНИЙ 7 КОРРЕКЦИЯ БТЗ 8 ОРГАНИЗАЦИЯ БАНКА ТЕСТОВЫХ ЗАДАНИЙ 9 КОРРЕКЦИЯ ТЕСТОВЫХ ЗАДАНИЙ 10 ПРЕДВАРИТЕЛЬНОЕ ШКАЛИРОВАНИЕ

ЭТАПЫ СОЗДАНИЯ БТЗ 11 ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТАЛЬНОГО ТЕСТИРОВАНИЯ 12 КОРРЕКЦИЯ ПОКАЗАТЕЛЕЙ БТЗ и ШКАЛЫ ОЦЕНИВАНИЯ 13 СЕРТИФИКАЦИЯ БТЗ

u u Система комплексной экспертизы качества тестовых материалов состоит из четырех основных этапов: Предварительная экспертиза качества тестовых материалов, целью которой является отбор авторского материала, соответствующего требованиям тестов. Экспертное оценивание (внутренняя экспертиза) качества тестов, проводимое после составления первого варианта теста. Тестологическая экспертиза, заключающаяся в проведении апробационного тестирования и расчета на основе его результатов статистических характеристик качества тестов и тестовых заданий. Комплексное оценивание качества тестовых заданий и тестов.

Основные показатели качества тестовых заданий при экспертизе 1. Компактность формулировки ТЗ и вариантов ответов 2. Свернутость ТЗ 3. Логичность (формулировка ТЗ в виде суждения) 4. Корректность (отсутствие лишних слов) 5. Достаточность (необходимое количество вариантов ответов) 6. Содержательность (соответствие ТЗ содержанию ГОС или учебной программе) 7. Значимость (уровень значимости содержания ТЗ) 8. Время вывода заключения(ответа) 9. Однозначность ТЗ 10. Ясность смысла тестовой ситуации

ЭКСПЕРТИЗА КАЧЕСТВА ПЕДАГОГИЧЕСКОГО ТЕСТА u Оценочный лист эксперта

Критерии отбраковки ТЗ u u u тестовое задание должно быть сформулировано в виде повествовательного предложения утвердительного вида; длина тестового задания должна быть меньше 250 символов, длина ответов не превышать 50; количество ответов для закрытой формы ТЗ должно быть от 4 до 6; ТЗ не должно содержать любой формы отрицания; запрещаются повторяющиеся фразы в дистракторах;

Критерии отбраковки ТЗ u u u u количество элементов в ТЗ на упорядочение и на соответствие не должно превышать 9; каждое ТЗ должно иметь хотя бы один ответ, помеченный как правильный; ТЗ не должно начинаться с предлога, частицы, союза; тестовое задание не допускает формы альтернативного вопроса; тестовое задание и варианты ответа к нему могут иметь поясняющие рисунки; по возможности, текст ТЗ не должен содержать сложноподчиненные конструкции; ТЗ, требующие открытый ответ, должны содержать в качестве эталонного ответа одно или два слова,

Математико-статистическая обработка эмпирических данных Интерпретация результатов обработки Статистика, возможно, знает все. Но ее знают не все. (Из статистических данных). Александр Самойленко

Подготовка к апробации Проверьте содержание и формулировку задач во взаимосвязи с другом u Распределите задания в порядке возрастания трудности u Рассчитайте время выполнения заданий u Подготовьте четкие инструкции для учащихся и ведущих апробацию u

Цели апробации тестовых заданий u u u Получение статистических характеристик апробируемых заданий (трудность, дифференцирующая способность и др. ). Получение экспертных характеристик апробируемых заданий (корректность формулировок, значимость для итогового (промежуточного) контроля, соответствие действующим учебникам и др. ). Выявление проблемных заданий.

Апробация тестовых заданий u u u Для получения достоверных результатов при проведении апробационных исследований необходимо, чтобы были выполнены следующие условия: Достаточная мотивированность тестируемых для данной работы Уровень прохождения учебного материала тестируемыми должен соответствовать уровню сложности и содержанию апробационного теста Ответственность и заинтересованность организаторов апробации должны отвечать поставленным задачам Процедура апробационных тестирований должна соответствовать условиям проведения реального испытания

Протокол апробации u u u u Протокол апробации теста по __________ название предмета Дата и время апробации___________________ Учебное заведение_____________________ Класс ___________________________ Количество вариантов теста _________________ Количество заданий в варианте теста _____________ Количество тестируемых __________________ Время тестирования_____________________ Замечания по процедуре тестирования ________________________________________________________ Замечания к содержанию тестовых заданий: Вариант теста, № тестового задания, суть замечания «___» _____ 200__ г.

Характеристики тестовых заданий u u u Показатель трудности заданий Коэффициент дискриминативности Процент учащихся, выбравших отдельные варианты ответа на каждое задание с выбором ответа или процент учащихся, выполнивших отдельные этапы задания со свободным ответом Надежность тестовых заданий Валидность

Этап математико-статистической обработки можно разбить на ряд шагов u Первый шаг связан с формированием матрицы тестовых результатов, в которой количественные данные представляются в систематизированной и сжатой форме, чтобы обеспечить их дальнейшую обработку и интерпретацию
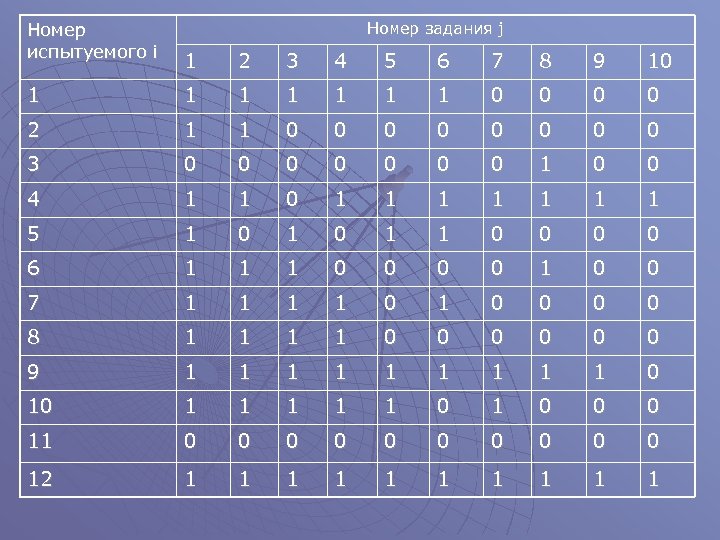
Номер испытуемого i Номер задания j 1 2 3 4 5 6 7 8 9 10 1 1 1 1 0 0 2 1 1 0 0 0 0 3 0 0 0 0 1 0 0 4 1 1 0 1 1 1 1 5 1 0 1 1 0 0 6 1 1 1 0 0 7 1 1 0 1 0 0 8 1 1 0 0 0 9 1 1 1 1 1 0 10 1 1 1 0 0 0 11 0 0 0 0 0 12 1 1 1 1 1

Второй шаг На втором шаге из матрицы тестовых результатов устраняются строки и столбцы, состоящие только из нулей или только из единиц u
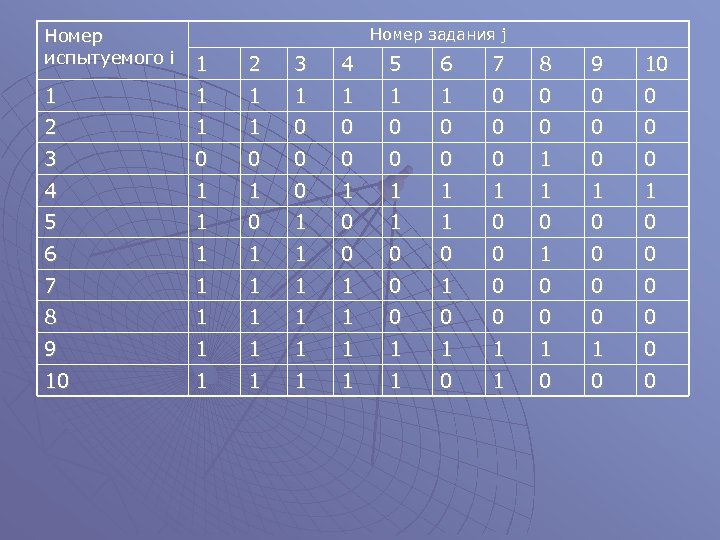
Номер испытуемого i 1 2 3 4 5 6 7 8 9 10 1 1 1 1 0 0 2 1 1 0 0 0 0 3 0 0 0 0 1 0 0 4 1 1 0 1 1 1 1 5 1 0 1 1 0 0 6 1 1 1 0 0 7 1 1 0 1 0 0 8 1 1 0 0 0 9 1 1 1 1 1 0 10 1 1 1 0 0 0 Номер задания j

Третий шаг связан с подсчетом индивидуальных баллов испытуемых и количеством правильных ответов испытуемых на каждое задание теста. Индивидуальный балл испытуемого получается суммированием всех единиц, полученных им за правильно выполненные задания теста. Например, 4 -й испытуемый выполнил правильно 9 заданий, поэтому его индивидуальный балл равен 9. В строке ответов 2 -го испытуемого стоят всего две единицы — его индивидуальный баллл Х= 2 u

u u Четвертый шаг На четвертом шаге осуществляется упорядочение матрицы результатов тестирования. Для этого производят перестановку столбцов, располагая числа R в порядке убывания Пятый шаг На пятом шаге производится графическая интерпретация эмпирических данных. Эмпирические результаты тестирования можно представить в виде полигона, гистограммы, сглаженной кривой или машинописного графика
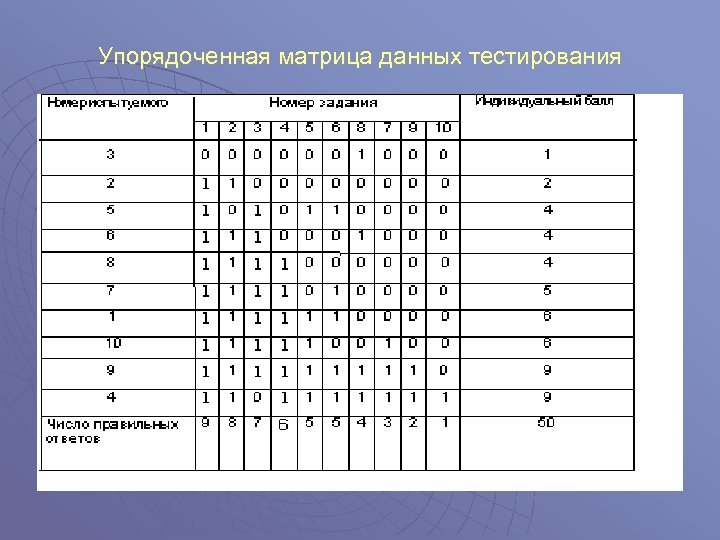
Упорядоченная матрица данных тестирования

Для построения кривых необходимо упорядочить результаты эксперимента Их можно записать в виде: u u несгруппированного ряда произвольной формы ранжированного ряда частотного распределения u распределения сгруппированных частот

Графическое представление результатов тестирования полигон и столбиковая гистограмма

u Шестой шаг На шестом шаге оцениваются меры центральной тенденции совокупности результатов, полученные при выполнении теста. Меры центральной тенденции предназначены для выявления «центрального положения» , вокруг которого в основном группируется множество значений рассматриваемого распределения данных

Гистограмма эмпирического распределения

u Среднее выборочное (среднее арифметическое) определяется суммированием всех значений совокупности и последующим делением на их число. Для совокупности индивидуальных баллов

u Среднее арифметическое индивидуальных баллов испытуемых для рассматриваемого выше примера матрицы будет

Седьмой шаг На седьмом шаге определяются описательные характеристики, служащие мерами изменчивости в группе данных по тесту u Для характеристик степени рассеяния отдельных значений вокруг среднего используются различные меры: размах, дисперсия, стандартное отклонение u

Размах измеряет на шкале расстояние, в пределах которого изменяются все значения показателя в распределении. Например, распределения индивидуальных баллов табл. 1 Размах равен 9 — 1=8. u Дисперсия. Подсчет дисперсии основан на вычислении отклонений каждого значения показателя от среднего арифметического в распределении. Для ученика с индивидуальным баллом выше среднего значение разности Хi-Хср будет положительно, а для тех, у кого результат ниже Xср , отклонение Xi-Xср меньше нуля. u

Дисперсия u u Если Хср=5 то Для 3 -го ученика d 3=x 3 -xср=1 -5=-4 Для 2 -го ученика d 2=x 2 -xср=2 - 5=-3… и. т. д. u u Получаем – Мера изменчивости(дисперсия) обозначается символом

Стандартное отклонение u Кроме дисперсии, для характеристики меры изменчивости распределения удобно использовать еще один показатель вариации, который называется стандартным отклонением. Стандартное отклонение равно корню квадратному из дисперсии:

u u Дисперсия играет важную роль в оценке качества нормативно-ориентированных тестов. Низкая дисперсия индивидуальных баллов говорит о слабой дифференциации испытуемых по уровню подготовки в тестируемой группе, т. е. о той ситуации, которая диаметрально противоположна основной цели создания нормативно-ориентированного теста. Излишне высокая дисперсия, характерная для случая, когда все учащиеся отличаются по числу выполненных заданий, также грозит неприятными последствиями и требует переработки теста. При переработке теста следует руководствоваться простым правилом: величину X сравнивают с утроенным стандартным отклонением. Если это равенство выполняется, то дисперсия оптимально высока и можно принять гипотезу о нормальности распределения.

Трудность заданий u 1. 2. 3. СУБЪЕКТИВНАЯ u СТАТИСТИЧЕСКАЯ Условия Определяется долями решения задачи выборки решивших и Уровень не решивших задачу формирования испытуемых основных навыков Состояние испытуемого

Трудность заданий u Характеристика задачи теста, отражающая статистический уровень её решаемости в данной выборке – Pj (доля правильных ответов). Рассчитывается как отношение числа тестируемых правильно выполнивших задание- Rj, к общему числу тестируемых- N.

Представление о трудности заданий теста легко получить путём анализа гистограммы, такой, как, например, на рисунке. В рассматриваемом примере явно просматриваются недостатки в подборе трудности заданий теста
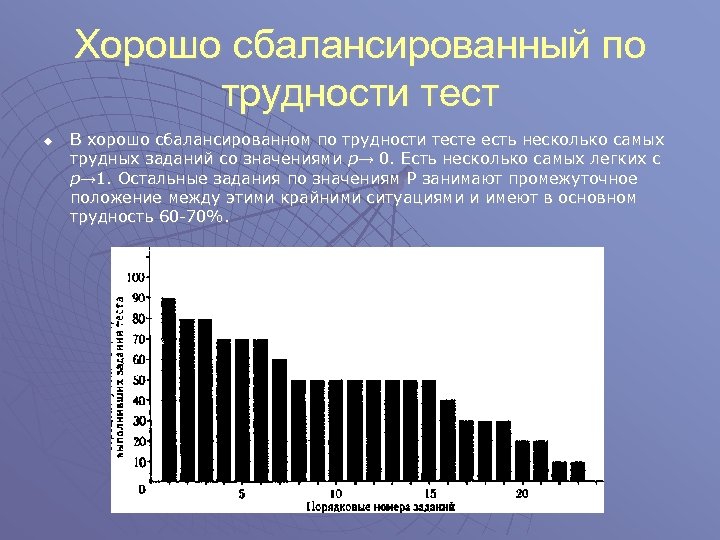
Хорошо сбалансированный по трудности тест u В хорошо сбалансированном по трудности тесте есть несколько самых трудных заданий со значениями р→ 0. Есть несколько самых легких с р→ 1. Остальные задания по значениям P занимают промежуточное положение между этими крайними ситуациями и имеют в основном трудность 60 -70%.

Норма трудности определяется разработчиком ТЗ и указывает субъективную величину того, насколько тяжело будет решить данное тестовое задание испытуемому с минимальным уровнем подготовки. Факторы, влияющие на норму трудности ТЗ • образ мышления, на который направлено ТЗ; • количество концептов, необходимых для решения ТЗ; • форма ТЗ; • глубина расположения ТЗ в спецификации; • количество заключений (вариантов ответов); • уровень значимости ТЗ.

Рекомендации по назначению нормы трудности 1. Норма трудности ТЗ может оцениваться с учетом количества используемых концептов, необходимых для поиска правильного решения. Под концептом в дальнейшем понимается некоторое умозаключение (формула, правило, аксиома и т. д. ), позволяющее приблизить правильное решение ТЗ. Чем больше шагов нужно выполнить для получения правильного ответа, тем выше норма трудности, тем сложнее считается ТЗ.

Рекомендации по назначению нормы трудности 2. Норма трудности ТЗ зависит от образа мышления, на который направлено ТЗ.

Рекомендации по назначению нормы трудности 3. Если ТЗ направлено на «опознание» какого-то объекта или на проверку «знания-знакомства» , то такое ТЗ следует считать простым.

Рекомендации по назначению нормы трудности 4. Если ТЗ направлено на выбор одного варианта ответа из многих с помощью знания всего одного концепта, то такое ТЗ следует считать простым.

5. Если ТЗ открытого типа направлено на выявление знания определения односложного базового термина, то такое ТЗ следует считать простым.

6. Если ТЗ направлено на применение усвоенных ранее знаний в типовых ситуациях (т. е. в тех ситуациях с которыми знаком испытуемый) или на проверку «знаний воспроизведения копии» , то такое ТЗ следует считать ТЗ среднего уровня сложности. К ТЗ такого уровня сложности следует относить высказывания конъюнктивного или дизъюнктивного вида. В некоторых случаях к ТЗ такого уровня сложности могут быть отнесены ТЗ на соответствие и порядок.

7. Если ТЗ направлено на применение усвоенных знаний и умений в нестандартных условиях (т. е. в условиях, ранее не знакомых испытуемому) или на проверку «знаний умения и применения» , то такое ТЗ следует считать сложным. К ТЗ такого уровня сложности относятся задания, сформулированные в виде утверждений импликативного типа. (если…то) Такие задания требуют применения рассуждений в форме дедуктивного, индуктивного вывода и аналогии, причем для получения окончательного ответа необходима некоторая последовательность умозаключения (несколько концептов).

8. Назначение нормы трудности можно производить с учетом формы ТЗ. При этом наиболее простой формой ТЗ считается закрытая форма. Самая сложная форма ТЗ - на упорядочение и на соответствие. Открытая форма довольно часто бывает у ТЗ со средним уровнем сложности.

9. Назначение нормы трудности можно осуществлять, исходя из принадлежности ТЗ основному и дополнительному материалам (уровень значимости ТЗ). Очевидно, что для каждой дисциплины есть определённый набор базовых понятий, например, прописанных в ГОСе, а есть понятия, относящиеся к дополнительному материалу, то есть материалу, который даётся лишь наиболее успешно обучающимся группам учащихся. Поэтому, если ТЗ раскрывает базовое понятие, то такое задание можно считать простым, если же ТЗ принадлежит к дополнительному материалу, то его можно считать сложным.

10. Назначение нормы трудности можно осуществлять, исходя из принадлежности ТЗ уровню «глубины» спецификации теста. Если ТЗ раскрывает самый нижний уровень иерархии спецификации теста (например, некоторое «Понятие» ), то такое задание будет легким. Принадлежность ТЗ средним уровням иерархии спецификации теста (например, некоторой «Теме» или «Подтеме» ) повышает норму трудности - средний уровень сложности. Наконец, ТЗ, относящееся к верхнему уровню, корню дерева иерархии (например, к «Разделу» , «Главе» ), можно считать сложным.

u 11. Увеличение количества дистракторов также влияет на увеличение нормы трудности ТЗ.

Факторы, влияющие на норму трудности ТЗ • образ мышления, на который направлено ТЗ; • количество концептов, необходимых для решения ТЗ; • форма ТЗ; • глубина расположения ТЗ в спецификации; • количество заключений (вариантов ответов); • уровень значимости ТЗ.

ДИСКРИМИНАТИВНОСТЬ ТЕСТОВОГО ЗАДАНИЯ Дискриминативностью (discriminatory power) называется способность задания дифференцировать учеников на лучших и худших Высокая дискриминативность важная характеристика удачного тестового задания

Значения rдис для теста из 42 заданий

u u u Значения индекса rдис для заданий теста обычно представляют собой десятичную дробь, принадлежащую интервалу [-1; 1 ]. Максимального значения 1, 00 индекс rдис достигнет в том случае, когда все ученики из подгруппы лучших верно выполнят j-е задание теста, а из подгруппы худших это задание не выполнит верно ни один ученик. В этом случае задание будет обладать максимальным дифференцирующим эффектом. Нулевого значения индекса rдис достигнет в том случае, когда в обеих подгруппах будут равны доли учеников, правильно выполнивших j-е задание теста. И наконец минимальное значение rдис = -1 будет в ситуации, когда данное задание теста все сильные ученики сделали неверно, а все слабые — верно. Естественно, что задания второго и третьего типа с rдис - 0 или rдис < 0 из теста следует удалить

Типичные недостатки u u u Излишняя сложность, запутанность формулировки Неоднозначность условий Очевидность решения Зависимость результатов от памяти или других индивидуальных особенностей испытуемого Абсурдность, нереальность вариантов ответов Появление двух или более правильных ответов, не оговоренное в условии

u u u Восьмой шаг предназначен для вычисления показателей связи между результатами учеников по отдельным заданиям теста. При оценке качества заданий важно понять, существует ли тенденция, когда одни и те же ученики добиваются успеха в какой-либо паре заданий теста Корреляция в широком смысле этого слова означает связь между явлениями и процессами

Коэффициент корреляции Пирсона

u Для оценки связи между результатами выполнения двух заданий теста коэффициент корреляции Пирсона необходимо преобразовать, поскольку результаты выполнения заданий представляются в дихотомической шкале. Преобразованный коэффициент Пирсона, вычисляемый по дихотомическим данным, называется коэффициентом «фи» . Где Рjl-доля испытуемых, выполнивших правильно оба задания теста, т. е доля тех, кто получил 1 по обоим заданиям; рj — доля испытуемых, правильно выполнивших j-е задание; qj = 1; рl — доля испытуемых, правильно выполнивших l-е задание теста, q=1 -pl
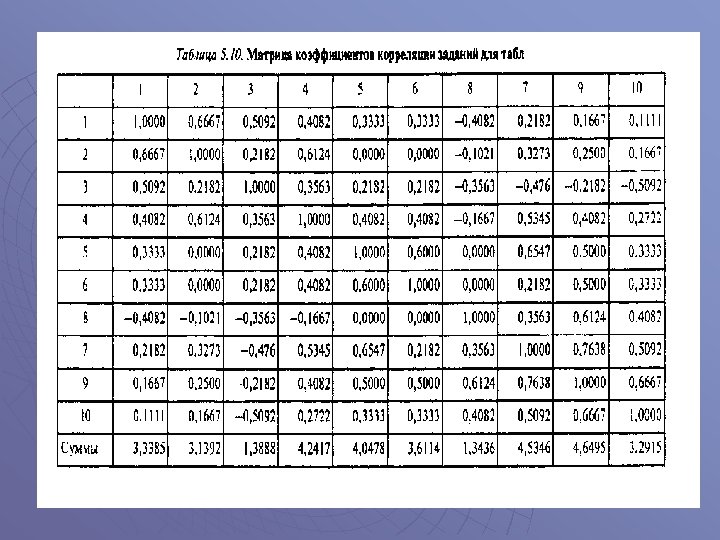

u Для тематических тестов высокая корреляция между заданиями неизбежна, так как задания отражают слабо варьирующее, исходное содержание, что вполне оправдано назначением теста

Анализ распределения ответов учащихся по предложенным вариантам ответа u u u Хорошие задания с выбором ответа, оценивающие достижение отдельного требования стандарта, должны иметь один выраженный максимум, соответствующий верному ответу. Неверные ответы учащихся должны распределяться, как правило, почти одинаково между всеми предложенными дистракторами. "Хороший" неверный ответ (диагностический) может быть выбран большим числом слабых учащихся. Если авторы оставляют задание, в котором один из ответов выбирают менее 5% испытуемых, то в этом случае задание, например, с 4 ответами, превращается в задание с 3 ответами, т. е. теряет один из возможных ответов и превращается в задание с меньшим числом ответов по сравнению с другими заданиями теста. Если ответы испытуемых распределены почти равномерно между всеми предложенными дистракторами и правильный ответ не выделяется, то возможно, что испытуемые отвечали наугад.

Надежность теста Надежность - это степень повторяемости или степень постоянства эмпирических измерений, т. е. результатов тестирования. Надежность теста, отражает точность и устойчивость результатов тестирования к воздействию посторонних случайных факторов. Тест называется надежным, если он дает одни и те же (или очень близкие) показатели для каждого испытуемого при повторном тестировании. Согласно классической теории тестов, развитой в основном на базе нормативно-ориентированного подхода к тестированию, наблюдаемый тестовый балл X состоит из двух компонентов: истинного и ошибочного, что можно выразить в формуле: X=T+E, где X - это индивидуальный балл испытуемого; Т - истинный балл испытуемого по данному тесту; Е - ошибочная компонента индивидуального балла. Если К-(надежность) близко к нулю, то интерпретация результатов тестирования ненадёжна.
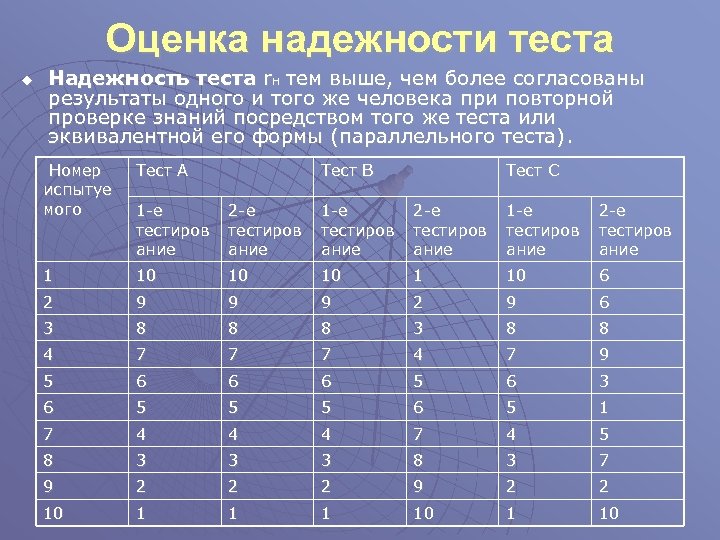
Оценка надежности теста u Надежность теста r. H тем выше, чем более согласованы результаты одного и того же человека при повторной проверке знаний посредством того же теста или эквивалентной его формы (параллельного теста). Номер испытуе мого Тест А Тест В Тест С 1 -е тестиров ание 2 -е тестиров ание 1 10 10 10 1 10 6 2 9 9 9 2 9 6 3 8 8 8 3 8 8 4 7 7 7 4 7 9 5 6 6 6 5 6 3 6 5 5 5 6 5 1 7 4 4 4 7 4 5 8 3 3 3 8 3 7 9 2 2 2 9 2 2 10 1 10

Надежность можно оценить: u Методом повторного тестирования u Методом параллельных форм u Методом расщепления теста

u Для подсчета коэффициента надежности используется формула

Надежность теста 1. Ретестовая надежность 2. Надежность расщепленных частей теста Коэффициент надежности Оценка надежности 0, 9 - 0, 99 Отличная 0, 8 - 0, 89 Хорошая 0, 7 - 0, 79 Удовлетворительная менее 0, 69 Неудовлетворительная

ИСТОЧНИКИ НЕУДОВЛЕТВОРИТЕЛЬНОЙ НАДЕЖНОСТИ ТЕСТА u u u u Субъективизм при оценке результатов выполнения заданий теста. Угадывание Отсутствие логической корректности формулировок заданий теста. Неоправданный выбор весовых коэффициентов Длина теста Отсутствие стандартной инструкции к тесту Другие источники снижения надежности.

Валидность u u u Валидность теста-характеристика инструментария, критерий его качества, который показывает, насколько хорошо тест делает то, для чего он был создан. Определить коэффициент валидности теста – значит определить, как выполнение теста соотносится с другими независимо сделанными оценками знаний испытуемых. Для определения валидности требуется независимый внешний критерий, то есть оценка эксперта (преподавателя). За коэффициент валидности принимают коэффициент корреляции результатов тестовых измерений и критерия.

Точечно-бисериальная корреляция u u Точечно-бисериальная корреляция позволяет оценить валидность задания и ответить на вопрос, как связано выполнение данного задания с выполнением всей работы в целом. Значение точечнобисериального коэффициента можно определить с помощью формулы, где X 1+ - средний балл выполнения теста для тех, кто правильно выполнил задание, X 0_ cредний балл выполнения теста теми, кто неправильно выполнил задание.

u u Числовые значения точечно-бисериального коэффициента могут меняться от 1 до -1. Положительная корреляция для верного ответа показывает, что испытуемые, хорошо справившиеся с работой, хорошо выполняют данное задание, т. е. выбирают или дают правильный ответ. Отрицательная или нулевая корреляция для верного ответа отражают случайный характер ответов учащихся или наличие каких-либо проблем в усвоении проверяемого материала. Можно установить следующий критерий отбора заданий по данному показателю: отбираются задания со значением точечно-бисериального коэффициента для правильного ответа, превышающим критическое значение 0, 20. Хорошим значением точечно-бисериального коэффициента считается интервал 0, 3 - 0, 5. Интервал 0, 2 - 0, 3 считается критическим.

ШКАЛИРОВАНИЕ РЕЗУЛЬТАТОВ u u Операция упорядочения исходных эмпирических данных путем перевода их в шкальные носит название шкалирования. Процесс шкалирования состоит в конструировании шкалы по определенным правилам и включает два этапа. Первый — сбор эмпирических данных. Второй этап — обработка и анализ, по результатам которого строится числовая система, представляющая собой шкалу.

ШКАЛИРОВАНИЕ РЕЗУЛЬТАТОВ Процесс шкалирования – это переход от целых баллов к производным показателям. Сводится к двум задачам: u 1) Определение достаточного уровня в некоторой шкале. u 2) Установление некоего положения в испытуемой группе. u

Z-ШКАЛА u u Наиболее простой метод выявления места результата i-го ученика (Xi) в сравнении с результатами других основан на подсчете отклонения балла Xi от среднего значения баллов X по группе тестируемых учащихся. Отклонение находят путем вычисления разности X— Хi Если разность X — Хi> 0, то результат i-го ученика выше среднего по группе. Отрицательное значение разности указывает на результат ниже среднего значения X. шкалированный результат i-го ученика находят по формуле

Для Z-шкалы результат i-го ученика находят по следующей формуле: Здесь Xi – первичный балл i-го испытуемого

Соотношение между баллами, оценочными эквивалентами и процентами испытуемых в 11 -баллльной шкале баллы 5 - баллы 11 - Оценочный эквивалент баллльной шкалы 2 Z-оценка Процент испытуемых Z<-2, 25 1 -2, 25<Z<-1, 75 3 3 Малоудовлетворительно -1, 75<Z<-1, 25 7 Удовлетворительно -1, 25<Z<-0, 75 12 5 Ниже среднего -0, 75<Z<-0, 25 17 6 Среднее -0, 25<Z<0, 25 20 7 Выше среднего 0, 25<Z<0, 75 17 8 5 Неудовлетворительно 4 4 Низшая оценка 2 3 1 Хорошо 0, 75<Z<1, 25 12 9 Очень хорошо 1, 25<Z<1, 75 7 10 Отлично 1, 75<Z<2, 25 3 11 Высшая оценка 2, 25<Z 1

ШКАЛА ОЦЕНКИ 5+ 5 54+ 4 43+ 3 32+ 2 2 - 12 11 10 9 8 7 6 5 4 3 2 1 Превосходно Отлично Почти отлично Более чем хорошо Хорошо Недостаточно хорошо Более чем удовлетворительно Удовлетворительно Малоудовлетворительно Более чем неудовлетворительно Нет знаний
83b159234451ab77c601a07ac2e78f96.ppt