Экскурс в историю математических символов Название произошло от

Экскурс в историю математических символов Название произошло от введенного Эйлером Черта сверху употреблялась очень долго. Знаки, выполняющие роль скобок появились в XVв. В Фигурные скобки появляются в сочинениях Виета (1593) немецкого термина Klammer – «скобки» . сочинении Шюке (1484) выражение, которое нужно До появления специальных символов перед СА В = С АВ Декарт, Ньютон, Лопиталь заключить в скобки, подчеркивается горизонтальной Широкое применение скобки получили лишь в первой выражением, которое нужно заключить в скобки, чертой. А – M+N половине XVIII века, благодаря Лейбницу и еще больше ставилось слово Collect или буквы сs от communis, Круглые скобки встречаются у Тартальи (1556), Затем у Эйлеру. u от universal или b, означающее binomial, и др. Жирара (1629). Это почти единственное, что осталось в a+b Бомбелли (1550) писал букву L перед L математике от символов , употребляемых Жираром. выражением, а в конце выражения перевернутую букву. От такого обозначения произошли квадратные скобки. L

Мы знаем! Распределительный закон умножения. Раскрытие скобок a ( b + c ) = ab +ac

Мы знаем! Распределительный закон умножения. ( + ) = ab+ac ac Вынесение за скобки общего множителя

+ +(+) + –(–) – –(+)

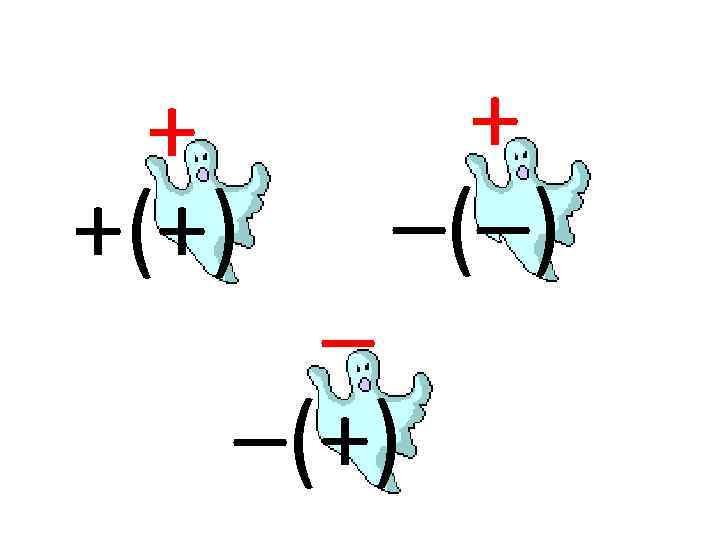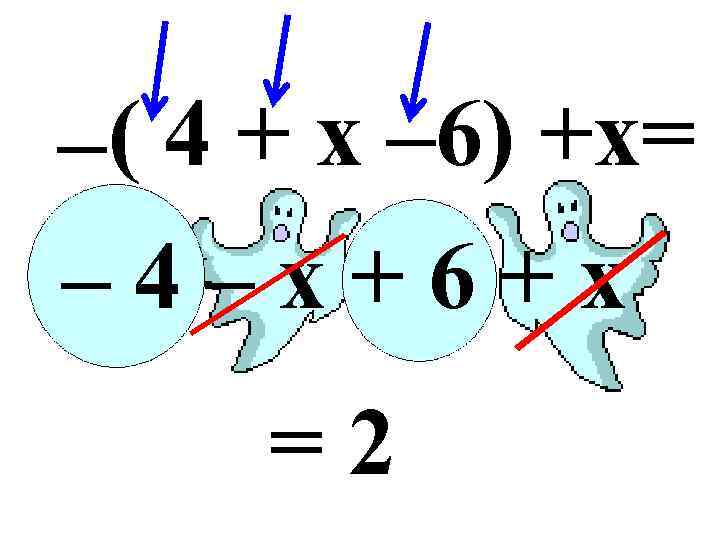–( 4 + x – 6) +x= – 4–x+6+x =2

Для раскрытия скобок используем распределительный закон умножения. -3(4 x – 5)= -12 x+15

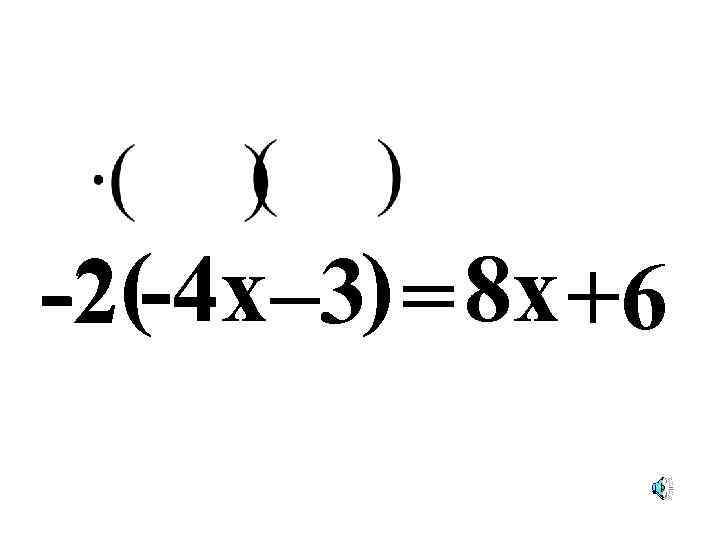-2(-4 x– 3) = 8 x +6

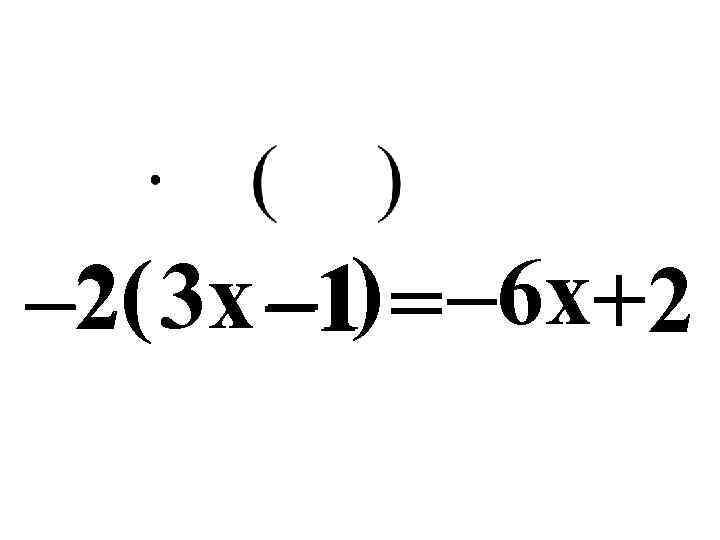– 2( 3 x – 1) = – 6 x+2

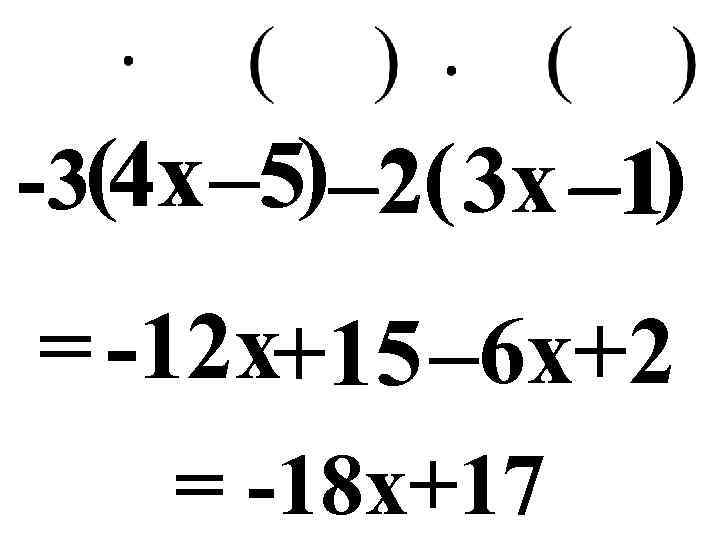-3(4 x – 5) – 2( 3 x – 1) = -12 x+15 – 6 x+2 = -18 x+17

• Уравнение – это равенство, содержащее букву, значение которой нужно найти. • Решить уравнение – это значит найти все его корни или доказать, что корней нет. • Корнем уравнения называется значение буквы, при котором уравнение обращается в верное равенство.

При решении уравнений с одной переменной используются следующие свойства: 1) Обе части уравнения можно менять местами ( если а = b, то и b = а). 2) Если в уравнении перенести слагаемое из одной части в другую, изменив его знак на противоположный, то корень уравнения не изменится; 3) Если обе части уравнения умножить или разделить на одно и то же число ≠ 0, то корень уравнения не изменится.

Алгоритм решения уравнения 1. Раскрыть скобки. 2. Перенести слагаемые, содержащие переменную, в одну часть уравнения, а числа без переменной – в другую часть, поменяв их знак на противоположный. 3. Упростить: привести подобные слагаемые. 4. Найти корень уравнения. 5. Сделать проверку.

Примеры решения уравнений 4(х + 5) = 12; 4(х + 5) = 12 |: 4; 4 х + 20 = 12; х+5 = 3; 4 х =12 – 20; х = 3 – 5; 4 х = – 8; х= – 2; х = – 8 : 4; х = – 2.

Чтобы сумму разделить на число, можно КАЖДОЕ СЛАГАЕМОЕ разделить на это число. 13 х – 26 = – 130; 13 х – 26 = – 130 |: 13; 13 х = – 130+26; х – 2 = – 10; 13 х = – 104 |: 13; х = – 10+2; х = – 8. х = – 8; Самостоятельно: 17 х – 34 = – 170

–+ -3 x + 7 = – x – 9 – 2 x= – 16 х= 8 Слагаемое можно переносить из одной части уравнения в другую, изменяя его знак.

Проверь и исправь ошибки! 7 х +5 = 9 х – 11; 7 х – 9 х = – 11 – 5 ; – 2 х = 16 |: (-2); х = – 8. Самостоятельно: 5 х – 3 = 3 х– 11

Чтобы произведение разделить на число, можно только один из множителей разделить на это число, и результат умножить на другой множитель! 5(х – 6) = 15(х – 8); 5(х – 6) = 15(х– 8) |: 5; 5 х – 30 = 15 х – 120; х – 6 = 3(х – 8); 5 х – 15 х = – 120 +30; х – 6 = 3 х – 24; – 10 х = – 90 |: (– 10); х – 3 х = – 24 +6; х = 9; – 2 х = – 18 |: (– 2); х = 9. Самостоятельно: 4(х+273) = 12(х– 17)

Примеры решения уравнений •

Примеры решения уравнений •

Найди и исправь ошибки: 3 (х + 6) + 4 = 8 – ( 5 х + 2) 3 х + 18 + 4 = 8 – 5 х – 2 3 х + 5 х = - 18 – 4 + 8 - 2 8 х = 16 : 8 х = 2

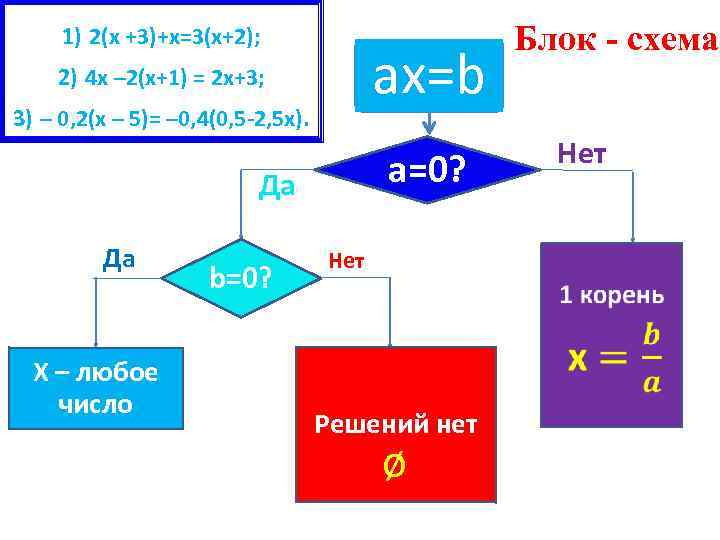1) 2(х +3)+х=3(х+2); aх=b 2) 4 х – 2(х+1) = 2 х+3; 3) – 0, 2(х – 5)= – 0, 4(0, 5 -2, 5 х). Х – любое число b=0? Нет a=0? Да Да Блок - схема Нет Решений нет ø

Задания для самостоятельного решения 1) 2 х + 5 = 2 (- х + 1) + 11; 2) 6 у – 3(у – 1) = 4 + 5 у; 3) 4 ( s – 1) – 3 = - ( s + 7) + 8; 4) 3(0, 4 t + 7) – 4(0, 8 t – 3) = 2; 5) 12 + 4(x – 3) – x = – (5 – 3 х) + 9; 6) 6(1 + 5 а) = 5(1 + 6 а) +1.

Задания для самостоятельного решения. Ответы. 1) 2) 3) 4) 5) 6) 2 - 0, 5 1, 6 -15, 5 нет корней х – любое число

Две фотографии набрали одинаковое число «лайков» . Когда первая фотография набрала ещё 30 «лайков» , а вторая 10, то количество «лайков» у первой фотографии стало в 1, 5 раза больше, чем у второй. Сколько «лайков» было у каждой фотографии первоначально? I фотография было +30 стало х II фотография = в 1, 5 раза > +10 х Показать (3)

Было 1 фото 2 фото х х стало х+30 х+10 в 1, 5 раза < Две фотографии набрали одинаковое число «лайков» . Когда первая фотография набрала ещё 30 «лайков» , а вторая 10, то количество «лайков» у первой фотографии стало в 1, 5 раза больше, чем у второй. Сколько «лайков» было у каждой фотографии первоначально? Уравнение: Х+30=1, 5(х+10) Х+30=1, 5 х+15 х – 1, 5 х = 15 – 30 – 0, 5 х = – 15 0, 5 х = 15 |: 0, 5 Х = 30; значит 30 «лайков» было первоначально. Ответ: 30 «лайков» было первоначально у каждой фотографии.

Реши самостоятельно. В первом волейбольном матче было забито в три раза больше мячей, чем во втором. Если бы в первом матче пропустили 41 мяч, а во втором забили ещё 7, то число мячей, забитых в этих матчах было бы одинаковым. Сколько очков набрала эта команда за два матча? Ответ: 96 мячей было забито за эти матчи.

Древнегреческая задача. – Скажи мне знаменитый Пифагор, сколько учеников посещают твою школу и слушают твои беседы. – Вот сколько, – ответил Пифагор, – половина изучает математику, четверть – природу, седьмая часть проводит время в размышлении, и, кроме того, есть еще три женщины.

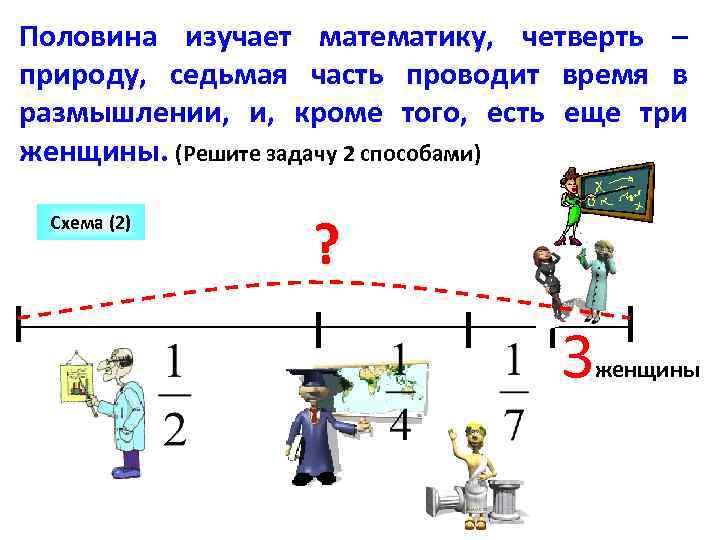Половина изучает математику, четверть – природу, седьмая часть проводит время в размышлении, и, кроме того, есть еще три женщины. (Решите задачу 2 способами) Схема (2) ? 3 женщины