Экономикоматематические методы Модель межотраслевого баланса Межотраслевое моделирование

Экономикоматематические методы Модель межотраслевого баланса

Межотраслевое моделирование является частью макроэкономического моделирования и служит для анализа и оценки состояния общего экономического равновесия национальной экономики. Национальная экономика в межотраслевом балансе представлена рядом чистых отраслей, связанных между собой финансовыми потоками от реализации продукции, работ и услуг. Чистые отрасли – это условные отрасли, представляющие производство одного или нескольких однородных продуктов.

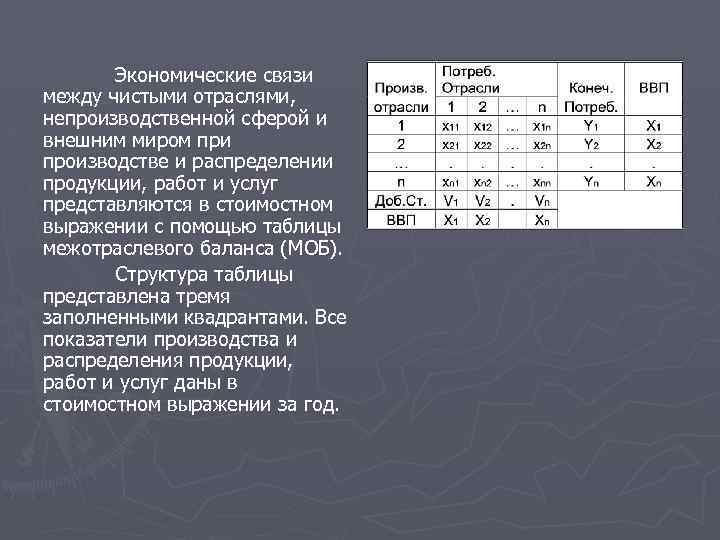
Экономические связи между чистыми отраслями, непроизводственной сферой и внешним миром при производстве и распределении продукции, работ и услуг представляются в стоимостном выражении с помощью таблицы межотраслевого баланса (МОБ). Структура таблицы представлена тремя заполненными квадрантами. Все показатели производства и распределения продукции, работ и услуг даны в стоимостном выражении за год.

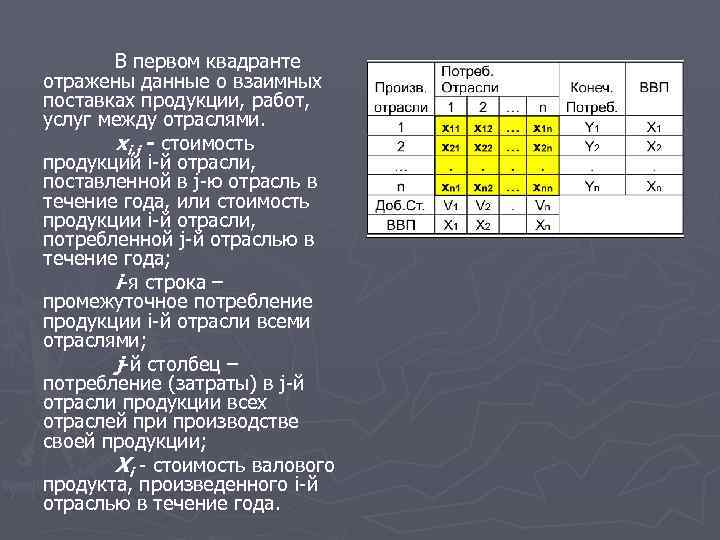
В первом квадранте отражены данные о взаимных поставках продукции, работ, услуг между отраслями. xi, j - стоимость продукции i-й отрасли, поставленной в j-ю отрасль в течение года, или стоимость продукции i-й отрасли, потребленной j-й отраслью в течение года; i-я строка – промежуточное потребление продукции i-й отрасли всеми отраслями; j-й столбец – потребление (затраты) в j-й отрасли продукции всех отраслей при производстве своей продукции; Xi - стоимость валового продукта, произведенного i-й отраслью в течение года.

Второй квадрант называется квадрантом конечного использования (потребления) или конечного спроса. В нем представлено конечное использование продукции отраслей, распределенное на: Сi - конечное потребление; Ii – инвестиции; Ei – экспорт; Mi – импорт; Ei – Mi - сальдо во внешней торговле. Конечное потребление включает потребление домашних хозяйств (населения), государства и некоммерческих организаций.

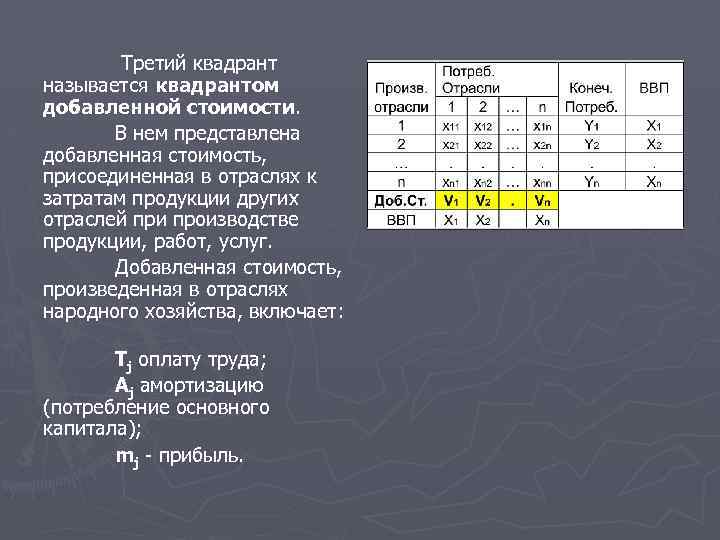
Третий квадрант называется квадрантом добавленной стоимости. В нем представлена добавленная стоимость, присоединенная в отраслях к затратам продукции других отраслей при производстве продукции, работ, услуг. Добавленная стоимость, произведенная в отраслях народного хозяйства, включает: Tj оплату труда; Aj амортизацию (потребление основного капитала); mj - прибыль.

Балансовые соотношения

Для каждой строки справедливо соотношение баланса между производством и потреблением. Указанное отношение означает, что валовой продукт отрасли расходуется полностью на производственное и непроизводственное потребление.

Для любого столбца справедливо равенство. Это равенство представляет стоимостную структуру продукта каждой отрасли. Равенство показывает, что стоимость валового продукта отрасли складывается из затрат других отраслей на его производство и стоимости условно чистой продукции, не производящейся внутри производственной системы.

Еще одно важное соотношение межотраслевого баланса показывает, что суммарный конечный продукт равен суммарной условно-чистой продукции.

Математическая модель межотраслевого баланса

Предположим, что для выпуска некоторого объема продукции отрасли номер i необходимо затратить валовую продукцию отрасли номер j в количестве ai, j xj, где ai, j – постоянный коэффициент, обусловленный существующими технологиями и определяемый по данным отчетного баланса или другим источниками. Соотношение выражает условие линейной зависимости объема производства от издержек или линейности существующей технологии. Коэффициенты называются коэффициентами прямых материальных затрат или технологическими коэффициентами.

Коэффициент прямых материальных затрат отражает стоимость продукции отрасли номер i, вложенной в производство единицы продукции отрасли номер j в стоимостном выражении. Матрицу А называют матрицей прямых материальных затрат. Технологические коэффициенты обладают рядом свойств.

Используя, приведенные выше, балансовые соотношения и коэффициент прямых материальных затрат построим балансовую модель, которая получила название «модель Леонтьева» .

Задачи

Задача 1 По заданному вектору конечного потребления Y = (Y 1 , Y 2 , Y 3 , …, Yn) найти вектор валового продукта. Эта задача содержит основной вопрос межотраслевого анализа: Каким должно быть валовое производство каждой отрасли, чтобы экономическая система в целом произвела заданное количество конечного продукта?

Запишем систему уравнений в матричной форме. Разрешимость системы уравнений в положительных числах зависит от свойства матрицы А, называемого продуктивностью матрицы. Матрица А называется продуктивной, если существует вектор Х > 0 такой, что X > A x X. Смысл этого неравенства заключается в том, что затраты на выпуск продукта должны быть меньше его стоимости. Достаточными условиями продуктивности матрицы являются неравенства:

Для того, чтобы матрица А была продуктивной необходимо и достаточно существования неотрицательной матрицы B = (E - A)-1, которую называют обратной матрицей Леонтьева. Решение системы в матричном виде X=Bx. X Или в развернутой форме.

Задача 2 По заданному вектору валового продукта X = (X 1, X 2, X 3, …, Xn) найти вектор конечного потребления Y = (Y 1, Y 2, Y 3, …, Yn) Какое количество продукции в стоимостном выражении можно направить на потребление при заданном объеме валового продукта?

Индексы цен в модели межотраслевого баланса

Предположим, что в следующем периоде планируется изменение цен в каждой отрасли i в pi раз при тех же натуральных значения векторов Х и Y. Тогда таблица межотраслевого баланса будет выглядеть следующим образом.

В этой таблице также выполняются балансовые соотношения.

Zj – новые значения добавленной стоимости. Разделив уравнения на вектор Хj получим уравнения для вектора индекса цен (модель равновесных цен).

Запишем в матричном виде: p – вектор-строка индексов цен; d – вектор-строка долей добавленной стоимости в валовом продукте отраслей в новом варианте межотраслевого баланса. Таким образом, для определения вектора индекса цен достаточно решить систему уравнений.

Полученную математическую модель называют моделью равновесных цен. Модель равновесных цен позволяет прогнозировать цены на продукцию отраслей при известных значениях величины норм добавленной стоимости. Кроме того, модель равновесных цен позволяет прогнозировать изменение цен и инфляцию, как следствие изменения цены в одной из отраслей.

Модель межотраслевого баланса позволяет решать следующие экономические задачи. 1. Определение матрицы прямых и полных материальных затрат по таблице межотраслевого баланса. 2. Определение вектора валовой продукции по заданному вектору конечного потребления. 3. Определение вектора конечного потребления по заданному вектору валовой продукции. 4. Определение неизвестных значений компонентов векторов добавленной стоимости и валового продукта по отдельным отраслям. 5. Определение индексов цен и построение новой таблицы межотраслевого баланса по новым значениям добавленной стоимости. 6. Определение коэффициента прямых затрат по заданной матрице прямых материальных затрат и вектору конечного потребления.

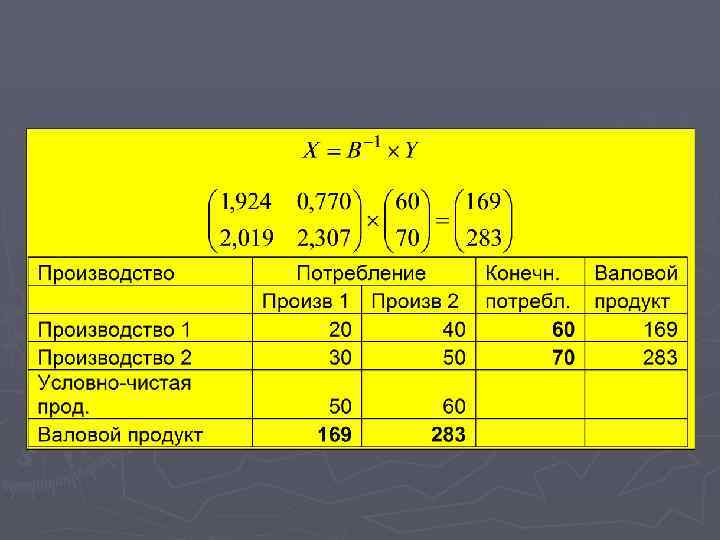
Пример

Таблица межотраслевого баланса

Задача 1 Зададим новые значения вектора конечного потребления.

Определение индекса цен

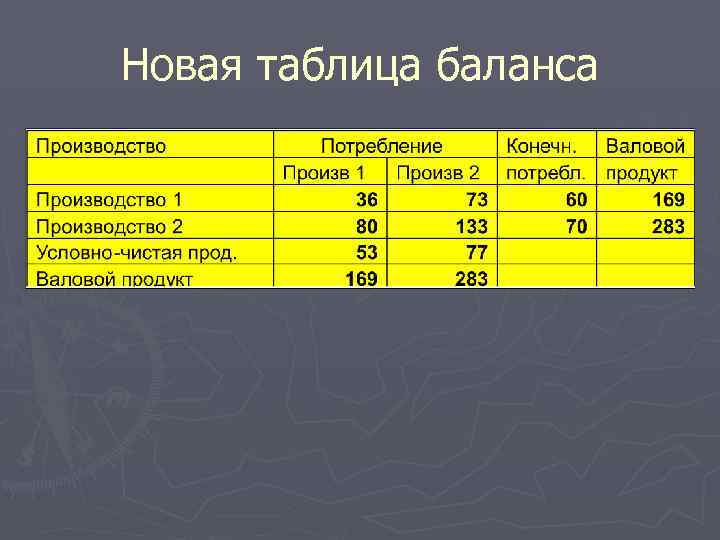
Новая таблица баланса

Динамическая модель Леонтьева

Рассмотренная модель межотраслевого баланса является статической, поскольку в ней все соотношения отнесены к одному определенному моменту времени. Инвестиции (капиталовложения), представленные во втором квадранте таблицы межотраслевого баланса, включены в конечный продукт. В этой модели не анализируется распределение, использование и эффективность инвестиций.

Для изучения процесса развития объектов, событий и явлений используются динамические модели. Для построения динамической модели межотраслевого баланса необходимо капиталовложения выделить из состава конечной продукции и исследовать их структуру, а также влияние на рост объема производства.

В математическую модель необходимо ввести матрицу капиталовложений, элементы которой показывают, какое количество продукции отрасли номер i направлено в отрасль номер j в качестве производственных капитальных вложений в основные и оборотные средства.

В динамической модели конечный продукт включает продукцию отрасли номер i, идущую в личное и общественное потребление, накопление непроизводственной сферы, незавершенное строительство, экспорт. Все показатели выражаются в стоимостной мере. Межотраслевые потоки капитальных вложений относятся к периоду (t-1, t). Динамика изменений задается дополнительным соотношением.

Экономический смысл коэффициентов φ заключается в следующем. Они показывают, какое количество продукции отрасли i должно быть вложено в отрасль номер j для увеличения выпуска ее продукции на единицу в рассматриваемых единицах измерений. Эти коэффициенты называются коэффициентами капитальных вложений или коэффициентами приростной фондоемкости.

Данная модель называется дискретной динамической моделью межотраслевого баланса Леонтьева (ДМОБ) и представляет собой систему линейных разностных уравнений 1 -го порядка. Для исследования этой модели необходимо задать значения X(0) и Y(0). Решением системы будут значения векторов X(t) и Y(t) для моментов времени t=1, 2, 3, …T.