ЭКОНОМИКОМАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ ВВЕДЕНИЕ Данный курс

ЭКОНОМИКОМАТЕМАТИЧЕСКИЕ МЕТОДЫ И МОДЕЛИ

ВВЕДЕНИЕ Данный курс охватывает достаточно обширный круг математических методов и моделей, в том числе и моделей оптимизации, которые нашли широкое применение в экономической науке.

ВВЕДЕНИЕ (продолжение) Например, в модели поведения потребителя предполагается, что он ищет максимум полезности. Модели фирмы основаны на предпосылке максимума прибыли для предпринимателя.

ВВЕДЕНИЕ (продолжение) Модели рынка - на предпосылке оптимальных стратегий участников обмена. Модели общего равновесия – на предпосылке цен оптимального плана. Модели воспроизводства – на предпосылке оптимального роста.

ВВЕДЕНИЕ (продолжение) При изучении дисциплины “ ЭММ и модели “ особое внимание уделяется не только изучению известных моделей и методов моделирования, но и анализу этих моделей, применению их на практике с учетом конкретных условий.

Цели и задачи дисциплины Данный курс предназначен для студентов экономических специальностей и направлен на изучение экономики с помощью математических моделей на макро – и микро – уровне, а также в разряде ее важнейших функциональных подсистем ( производственной, финансово – кредитной, социальной и др. )

Для достижения поставленной цели студенты должны освоить: n n n основные понятия и типы изучаемых моделей; роль и место математического моделирования в различных областях экономики и управления; практическое применение методов и моделей в области постановки и решения задач экономического анализа, прогнозирования и оптимального выбора.

СОДЕРЖАНИЕ КУРСА n n Задачи линейного программирования Двойственные задачи линейного программирования Транспортные задачи линейного программирования Модели целочисленного линейного программирования.

СОДЕРЖАНИЕ КУРСА (продолжение) n n Модели динамического программирования. Теория игр и принятие решений. Сетевое моделирование. Моделирование потребительского поведения и спроса.

СОДЕРЖАНИЕ КУРСА (продолжение) n n Моделирование и прогнозирование покупательского спроса. Моделирование ценовой политики. Моделирование поведения производителей. Моделирование взаимодействия потребителей и производителей.

Список рекомендуемой литературы (основная) n n n К. А. Багриновский, В. М. Матюшок. Экономико-математические методы и модели. – М. : ИРУНД, 1999. О. О. Замков, А. В. Толстопятенко. Математические методы в экономике. – М. : ДИС, 1997. Н. Ш. Кремер, Б. А. Путко. Исследование операций в экономик – М. : ЮНИТИ, 1997

Список рекомендуемой литературы (основная (продолжение)) n n n К. А. Багриновский, В. М. Матюшок. Экономико-математические методы и модели. – М. : ИРУНД, 1999. В. В. Федосеев. Экономикоматематические методы и модели в маркетинге. - М. : ЮНИТИ, 2001. Е. В. Бережная, В. И. Бережной. Математические методы моделирования экономических систем. – М. : Финансы и статистика, 2001.

Дополнительная литература n n n С. А. Жданов. Математические модели и методы в управлении. – М. : Дело и Сервис, 1998. Ю. П. Иванов. А. В. Лотов. Математические модели в экономике. – М. : Наука. 1979 А. С. Солодовников. Математика в экономике. - М. : Финансы и статистика, 1999.

ОБЩАЯ И ОСНОВНАЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Общей ЗЛП называется задача, которая состоит в определении оптимального (максимального или минимального) значения линейной функции

(продолжение) при условиях

Определение Совокупность чисел удовлетворяющих ограничениям ЗЛП, называют допустимым решением (или планом).

Определение Оптимальным решением ЗЛП называют допустимое решение при котором целевая функция принимает максимальное или минимальное значение.

Определение Основной (или канонической) ЗЛП называется задача, которая состоит в определении оптимального значения целевой функции, при условии, что система ограничений представлена в виде системы уравнений

(продолжение) при ограничениях

Определение Стандартной (или симметричной) ЗЛП называется задача, которая состоит в определении оптимального значения целевой функции, при условии , что система ограничений представлена в виде системы неравенств

(продолжение) при ограничениях

ТРАНСПОРТНАЯ ЗАДАЧА Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления A 1, A 2, …, Am в n пунктов назначения В 1, В 2…, Вn При этом в качестве критерия оптимальности берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки.

(продолжение) n Математическая модель транспортной задачи сводится к минимизации целевой функции, выражающей суммарные затраты на перевозку всего груза

(продолжение) при ограничениях

Определение Всякое неотрицательное решение системы ограничений транспортной задачи, определяемое матрицей, называют допустимым решением (или планом) транспортной задачи.

Определение План при котором целевая функция принимает минимальное значение, называется оптимальным.

Определение n Тарифы или стоимости перевозок единицы груза сij также задаются матрицей, которая называется матрицей транспортных издержек или матрицей стоимостей

Обычно исходные данные транспортной задачи записывают в виде таблицы Bj Ai B 1 B 2 A 1 c 11 x 11 c 12 x 12 A 2 c 21 x 21 c 22 x 22 … … Am Потребности Bn Запасы … … c 1 n x 1 n a 1 … cm 1 cm 2 xm 1 xm 2 b 1 … c 2 n x 2 n a 2 … … b 2 … … cmn xmn bn … am ∑a¡=∑bj

Необходимое и достаточное условие разрешимости транспортной задачи Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, то есть, чтобы выполнилось равенство (балансовые условия).

Определение исходного допустимого решения Первоначальное распределение перевозок Xij соответствует первому допустимому решению. Существуют различные методы получения первого допустимого решения.

Метод “ северо-западного угла“ Метод заключается в том, что заполнение клеток таблицы начинают с левой верхней клетки (северо-западная часть таблицы) для перевозки x 11 и продолжают вниз и вправо, заканчивая клеткой для перевозки xmn. При этом способе распределения на тарифы cij не обращают внимания.

Метод “наименьшей стоимости” Метод заключается в том, что заполнение клеток таблицы начинают с клетки, имеющей наименьшую стоимость перевозки. Если таких клеток несколько, то следует выбрать любую из них.

Перераспределение перевозок транспортной таблицы с целью улучшения решения происходит по циклу.

Цикл пересчета Циклом пересчета в транспортной таблице называют несколько клеток, соединенных замкнутой ломаной линией, которая в каждой клетке совершает поворот на 900.

Моделирование потребительского поведения и спроса

Аксиомы n. Ненасыщаемость n. Совершенность n. Транзитивность n. Рефлексивность

Полезность В теории порядковой полезности понятие полезность означает не что иное как порядок предпочтения. Потребитель выбирает предпочтительный набор благ из всех доступных для него.

Функция полезности является индикатором предпочтения, поскольку она обладает следующим характеристическим свойством: тогда и только тогда, когда

Функция полезности (продолжение) рассматривается как некоторая монотонно возрастающая функция, определенная на множестве потребительских наборов

Свойства функции полезности 1. С ростом потребления любого блага полезность растет. Частные производные функции полезности, определяющие предельную полезность всегда положительны

(Продолжение) 2. Небольшой прирост блага при его первоначальном отсутствии резко увеличивает полезность

(Продолжение) 3. Предельная полезность каждого блага уменьшается, если объем его потребления растет, то есть каждая дополнительная единица приобретенного блага используется менее эффективно. Скорость роста полезности замедляется. В этом случае вторые производные функции полезности отрицательны

(Продолжение) 4. При очень большом объеме блага его дальнейшее увеличение не приводит к увеличению полезности

(Продолжение) 5. Предельная полезность каждого блага увеличивается, если растет количество другого блага. В этом случае смешанные производные второго порядка положительны

продолжение Здесь благо, количество которого фиксировано, оказывается относительно дефицитным, поэтому дополнительная его единица приобретает большую ценность и используется более эффективно. Данное свойство справедливо не для всех благ. Если блага могут полностью замещать друга в потреблении, то это свойство не выполняется, но оно гарантирует выпуклость вниз кривых безразличия.

Предельная норма замещения благ первого блага вторым благом, обозначается (marginal rate of substitution) и показывает на сколько единиц увеличится (уменьшится) потребление второго блага, при уменьшении (увеличении) второго блага на единицу без изменения функции полезности.

Предельная норма замещения благ n n n Равна обратному соотношению их предельных полезностей. Знак минус говорит о том, что предельная норма замещения благ есть величина убывающая и увеличение количества одного блага приводит к уменьшению количества другого блага. Итак, кривые безразличия являются кривыми взаимозаменяемости благ, они отражают пропорции замены благ.

Бюджетным множеством называется множество всех наборов благ, которые может приобрести потребитель, имея доход I, где Р –вектор цен, Х – вектор благ.

Бюджетная линия – геометрическое место точек всех комбинаций благ, стоимость которых равна определенной сумме. Она характеризует реальную покупательскую способность потребителя благ и соотношение цен этих благ.

Сформулируем задачу о максимальном выборе потребителя. Имеется потребитель с определенным доходом I, предназначенным для приобретения набора благ по ценам соответственно. Ограниченность возможного выбора потребителя выражается с помощью бюджетного ограничения. Требуется найти максимум функции полезности.

Задача о максимальном выборе потребителя сводится к обычной задаче отыскания условного экстремума целевой функции полезности. Решение этой задачи на условный экстремум находится при помощи метода множителей Лагранжа. Строим функцию Лагранжа относительно λ и Хi. Где множитель Лагранжа является оптимальной оценкой дохода.

Условия оптимальности решения Необходимые условия оптимальности решения определяются системой ограничений

Моделирование покупательского спроса

Функциями спроса n n называются функции, отражающие зависимость объема спроса на различные виды благ от комплекса факторов, влияющих на него. Такие функции применяются в аналитических моделях спроса и потребления и строятся на основе информации о структуре доходов населения, ценах на товары и услуги, составе семей и других факторов.

Эластичность спроса характеризует чувствительность потребителя к изменению цен и показывает на сколько процентов изменяется спрос, при изменении цены на 1 %.

Если , то спрос неэластичен по цене. Если коэффициент эластичности близок к нулю, то спрос на товар практически не зависит от его цены. Это относится в основном к предметам первой необходимости. Цена P P D Q Количество Q

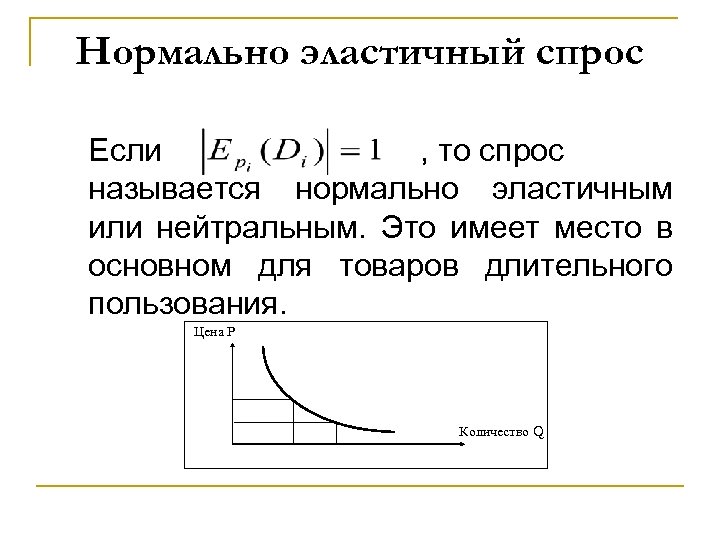Нормально эластичный спрос Если , то спрос называется нормально эластичным или нейтральным. Это имеет место в основном для товаров длительного пользования. Цена P Количество Q

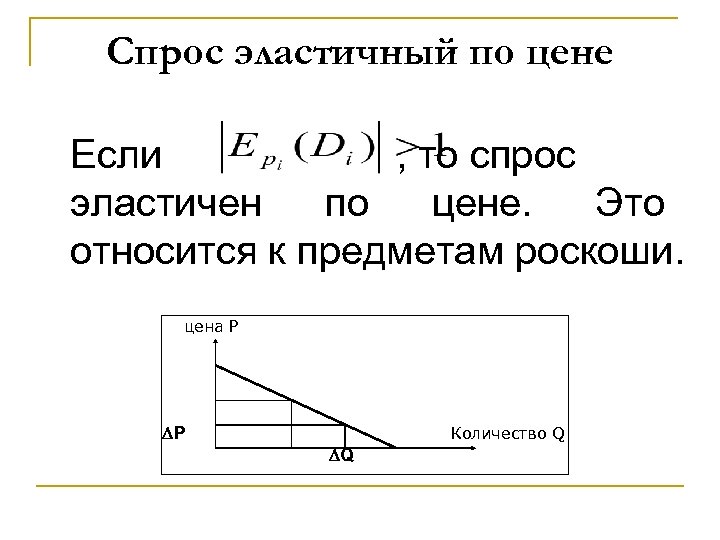Спрос эластичный по цене Если , то спрос эластичен по цене. Это относится к предметам роскоши. цена Р P Количество Q Q

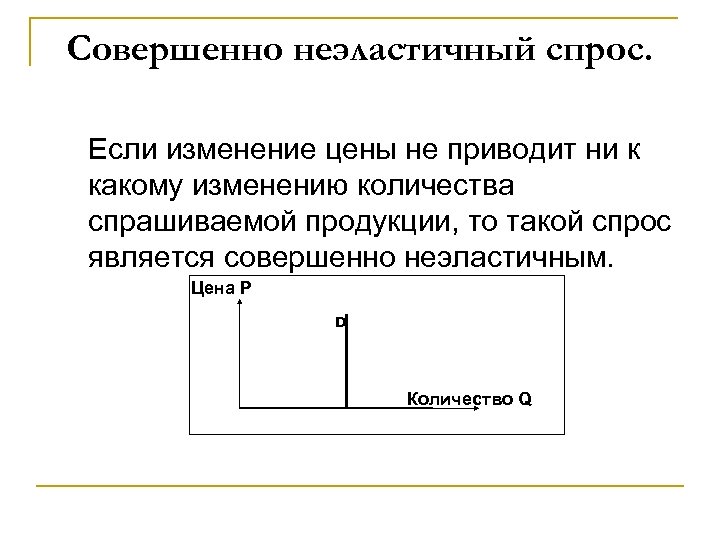Совершенно неэластичный спрос. Если изменение цены не приводит ни к какому изменению количества спрашиваемой продукции, то такой спрос является совершенно неэластичным. Цена P D Количество Q

Совершенно эластичный спрос Если самое малое снижение цены побуждает покупателей увеличивать покупки от нуля до предела своих возможностей, то такой спрос является совершенно эластичным. Цена P D Количество Q

Факторы ценовой эластичности спроса n Заменяемость. Чем больше хороших заменителей данного продукта предлагается потребителю, тем эластичнее бывает спрос на него. Эластичность спроса на продукт зависит от того, насколько узко определены границы этого продукта. n 2. Удельный вес в доходе потребителя. Чем больше места занимает товар в бюджете потребителя, при прочих равных условиях, тем выше эластичность спроса на него.

Факторы ценовой эластичности спроса (продолжение) n 3. Предметы роскоши и предметы необходимости. Спрос на предметы необходимости обычно является неэластичным, спрос на предметы роскоши обычно эластичен. n 4. Фактор времени. Спрос на продукт более эластичен, чем длиннее время для принятия решений. Это зависит от привычек потребителя , долговечности продукта.

Функция Энгеля (Степенного вида) Здесь γ имеет смысл коэффициента эластичности спроса относительно дохода и показывает на сколько процентов изменится спрос, если доход изменится на 1%.

Коэффициент эластичности спроса относительно дохода характеризует относительное (процентное) изменение спроса на какой-либо товар при изменении дохода потребителей на 1% и является мерой реакции спроса на изменение доходов потребителей.

Перекрёстная эластичность спроса по цене. n n Характеризует относительное (процентное) изменение величины спроса на один товар при изменении цены другого товара на 1%. Положительный знак перекрёстной эластичности спроса по цене свидетельствует о замещаемости товаров, а отрицательный - о дополняемости.

Моделирование ценовой политики

Имеем уравнение Вида

Система из линейного уравнения (1) n Относительно (n+1) неизвестного в матричной форме запишется следующим образом , (2) n где Т - означает транспонирование, Р- вектор – строка цен, U* - матрица Гессе, X - вектор – столбец спроса на товары.

Таким образом, увеличение цены на n-й товар привело к следующему изменению спроса на товары:

Рассмотрим такое увеличение дохода на d. M, которое компенсирует потребителю увеличение цены на dpn. Согласно теории потребления это означает, что полезность потребителя сохранилась на прежнем уровне, то есть dun=0. Используя получим

Условие постоянства полезности Теперь можем определить d. M, используя : то есть доход вырос ровно на столько, сколько необходимо было бы дополнительно затратить потребителю на приобретение n-го товара в прежнем объеме при увеличении цены на dpn.

(продолжение) Которые в матричной форме примут вид:

(продолжение) Решение уравнений находим с помощью обратной матрицы:

(продолжение) Таким образом, увеличение цены с компенсацией дохода приводит следующему изменению спроса: к

Объединим уравнения получаем уравнение Слуцкого, которое является стержнем теории полезности:

Ценный и малоценный товар

Валовой заменитель продукта Продукт L называется валовым заменителем продукта i если

Определение. Функция спроса Х*(р; м) обладает свойством валовой заменимости, если с увеличение цены на любой продукт I спрос на остальные продукты не убывает если же , то функция спроса обладает свойством сильной валовой заменимости.

Моделирование поведения производителя

Производственная функция Количественная взаимосвязь м/у затратами ресурсов и выпуском продукции может быть выражена в виде функции, которая получила название производственной.

Производственная функция Математическое выражение зависимости результатов производственной деятельности от обуславливающих эти результаты показателей факторов (ресурсов) называется ПФ.

Производственная функция С учётом изучаемой зависимости и задач исследования применяются многообразные виды ПФ. В простейшем случае рассматривается однофакторная ПФ, описывающая зависимость результативного показателя от одного показателя фактора.

Многофакторные ПФ n Чаще всего встречаются многофакторные ПФ, позволяющие изучать совместное влияние нескольких показателей факторов на величину изучаемого результативного показателя. Уравнение многофакторной ПФ имеет вид: или в неявном виде или где - вектор затрат, а – параметры.

Многофакторные ПФ могут быть так же представлены в виде системы взаимосвязанных уравнений как в аналитическом виде, так и в виде таблиц. , где - совокупность результативных показателей выпуска, - совокупность показателей факторов (ресурсов), - вектор, состоящий из р параметров, их конкретные числовые значения определяются на основе статистических данных с помощью корреляционных методов.

Производственная функция называется ПФ, представленной в каноническом виде, где - параметры постоянные величины, их конкретные числовые значения определяются на основе статистических данных с помощью корреляционных методов. Причем коэффициент α 0 означает размерность и зависит от избранной единицы измерений затрат и выпуска.

Степенные коэффициенты αi n где показывают ту долю в приросте конечного продукта, которую вносит каждый из сомножителей χi, т. е. они показывают на сколько процентов изменится количество выпускаемой продукции, если затраты соответствующего ресурса изменится на 1% следовательно это коэффициенты эластичности относительно затрат

Предельной производительностью i-го ресурса или предельным выпуском по i-му ресурсу называют первую частную производную ПФ и обозначают Эта величина показывает на сколько единиц изменится объём выпускаемой продукции (предельный продукт), если затраты соответствующего i-го ресурса изменится на единицу (при неизменном объёме других ресурсов).

Отношение предельной производительности i-го ресурса к его средней производительности даёт частную эластичность выпуска по i-му ресурсу. и показывает на сколько процентов изменится объём выпускаемой продукции, если затраты соответствующего ресурса изменятся на 1% (при неизменном объёме других ресурсов).

Свойства производственных функций n Без ресурсов выпуск невозможен , n При отсутствии хотя бы одного из ресурсов выпуск невозможен

Свойства производственных функций (продолжение). n Предполагается, что по крайней мере дважды дифференцируема, т. е. переменные X 1 и X 2 меняются непрерывно и результат производственной деятельности достаточно гладко меняется при изменении количества используемых ресурсов.

Свойства производственных функций (продолжение). n При увеличении затрат ресурсов выпуск продукции не уменьшается, т. е не убывает. Это значит, что и т. е. предельные производительности всех ресурсов положительны.

Свойства производственных функций (продолжение). Предельная производительность данного ресурса падает, если объём его затрат растёт, т. е. эффективность использования дополнительной единицы этого ресурса падает. Др. словами: величина прироста продукта на каждую дополнительную единицу i-го ресурса не растёт. Это закон убывающей эффективности. и

Свойства производственных функций (продолжение). Предельная производительность данного ресурса возрастает с ростом затрат другого ресурса, т. е. эффективность использования единицы данного ресурса возрастает с ростом затрат данного ресурса. и Отдача от расширения масштабов производства. Характеризует ПФ с точки зрения выпуска продукции пропорциональном изменении затрат.

Отдача от расширения масштабов производства. Характеризует производственную функцию с точки зрения выпуска продукции пропорциональном изменении затрат. При этом возможны три случая.

Отдача от расширения масштабов производства. 1. ПФ характеризуется постоянной отдачей от расширении масштаба производства, если выпуск возрастает в той же пропорции, что и затраты, т. е. увеличение, например, ресурсов в m раз приводит к увеличению продукции в m раз.

Отдача от расширения масштабов производства. 2. ПФ характеризуется возрастающей отдачей от расширения масштаба производства, если она возрастает в большей степени, чем все затраты. Например, увеличение ресурсов в m раз приводит к росту объёма продукции более чем в m раз. Экономически в этом случае можно говорить о положительном эффекте расширения масштабов производства

Отдача от расширения масштабов производства. 3. ПФ характеризуется убывающей отдачей от расширения масштаба производства, если она возрастает в меньшей степени, чем все затраты. Например, увеличение ресурсов в m раз приводит к росту объёма продукции менее чем в m раз. В этом случае имеет место отрицательный эффект от расширения масштабов производства.

Моделирование производителей и потребителей

Модель равновесных цен Пусть Vi - валовой выпуск продукции i-й отрасли. - столбец цен на рынке. Pi -цена единицы продукции i-й отрасли на рынке. Пусть A=(aij) - матрица прямых материальных затрат

(продолжение) Для первой отрасли рассчитаем стоимость материалов и комплектующих, которые были использованы в процессе производства. - затраты сырья на единицу продукции 1 -й отрасли. (1), где Р 1 V 1 - выручка, Y 1 - добавочная стоимость.

(продолжение) Очевидно, что Если А продуктивна, то и AT продуктивна, следовательно что для выполнимо

Модель международной торговли Имеется n стран с годовыми бюджетами Весь национальный доход Хi страны с номером i складывается от продажи своих товаров либо внутри страны, либо другим странам. Предположим, что мы имеем дело с уже сложившейся структурой международной торговли, а именно, что доля дохода i-й страны, кот тратится на покупку товаров (импорт) у страны с номером j, постоянна. В частности она не зависит от величины Xi этого дохода.

(продолжение) Эта гипотеза – предположение о линейности модели. Природа его следующая: действительно, у каждой страны существует постоянная компонента дохода (малозависящая от общей величины дохода), идущая на самые основные нужды. Т. к. Аij доли , то , т. е. здесь матрица Леонтьева и называется матрицей платёжного баланса международной торговли.

Пусть di доход от международной торговли i-й страны. . В матричном виде где d - доходы стран после первого тура торговли в соответствии с матрицей А. Считая, что ни одна страна не желает снижения своих доходов, требуется выяснить, согласятся ли они торговать в соответствии с матрицей А при существующем векторе доходов X. Ясно, что для этого необходимо, чтобы , т. е.

Теорема 1 Неравенство выполняется только, если т. е. .

Доказательство Предположим противное, т. е. Пусть для определённости Тогда следовательно противоречие, поэтому - обственное число матрицы А.

Теорема 2 Для любой квадратной матрицы, если сумма элементов каждого столбца =1, то матрица имеет собственное число.

Доказательство Рассмотрим матрицу Рассмотрим сумму строк данной матрицы. Она равна 0 следовательно строки линейно зависимы следовательно определитель=0 следовательно матрица вырожденная.

Доказательство (продолжение) Рассмотрим систему линейных уравнений которая имеет бесконечно много решений и решение данной системы. - X – собственный вектор, соответствующий собственному числу следовательно λ=1 матрицы А.

Утверждение Если А>0, то существует такой, что

Доказательство Пусть λА - число Фробениуса матрицы А. Рассмотрим. По теореме Фр. -Пер. X- собственный вектор, соответствующий собственному числу λ=1 и χ>0.

Теорема 3 Если в матрице платёжного баланса международной торговли для существует цепочка взаимного импорта из i-й страны в j-ю, то в уравнении

Доказательство Если в цепочке импорта, содержащей kэлементов 1 -й – i, а последний – j, то Для каждого ί≠j рассмотрим Рассмотрим матрицу X- собственный вектор матрицы В. n=λB число Фр. матицы В, B>0 следовательно по теореме Фр. -Пер. X>0.