Экономико-математические модели Тема 5 Модель Леонтьева затраты-выпуск Идея

Экономико-математические модели Тема 5. Модель Леонтьева «затраты-выпуск» Идея межотраслевого баланса впервые сформулирована в работах советских экономистов в 20 -х годах 20 века и затем получила развитие в трудах В. В. Леонтьева для изучения структуры американской экономики ssp@ugrasu. ru 1

Модель межотраслевого баланса § 11. Модель межотраслевого баланса Целью построения модели МОБ является анализ перетоков товаров между отраслями экономики, обеспечивающего соответствие объема выпуска суммарному спросу на товары. При этом не различаем товары и ресурсы (затраты) Как всякая модель МОБ является упрощением реальной ситуации. Перечислим основные из них: ssp@ugrasu. ru 2

Модель межотраслевого баланса Пусть производственный сектор экономики разбит на n «чистых» отраслей. Каждая отдельная отрасль производит только один продукт и разные отрасли производят различные продукты. Очевидно, что одни отрасли при своем производстве нуждаются в продукции других отраслей, т. о. выпуск каждого продукта либо затрачивается в производстве товаров либо удовлетворяет конечный спрос ssp@ugrasu. ru 3

Модель межотраслевого баланса Еще два важных предположения: т. е. объем выпуска прямо пропорционален объемам затрат ssp@ugrasu. ru 4

Модель межотраслевого баланса ФОРМАЛИЗАЦИЯ: Пусть xi – валовый продукт i-ой отрасли, yi – конечный продукт i-ой отрасли. Часть валового продукта потребляется другими отраслями, обозначим: xi 1 , xi 2 , …, xin. Всего на производственное потребление затрачивается: ssp@ugrasu. ru 5

Модель межотраслевого баланса Таким образом, возникает понятие баланса: ssp@ugrasu. ru 6

Модель межотраслевого баланса Изучая статистические данные экономисты, включая В. Леонтьева, заметили, что независимо от масштаба производства, коэффициенты , определяющие затраты i-й отрасли на производство единицы продукции j-й отрасли почти не меняются в годовом периоде производства ssp@ugrasu. ru 7

Модель межотраслевого баланса Определение: Коэффициенты, определяемые формулами (1) называют технологическими или коэффициентами прямых затрат. Следовательно, баланс можно записать: ssp@ugrasu. ru 8

Модель межотраслевого баланса Если технологическая матрица A известна (например, по данным прошлого года) и задан вектор конечной продукции y, то возникает задача нахождения вектора валовой продукции x. Таким образом, сущность межотраслевого баланса производства состоит в определении валового выпуска по заданному конечному продукту на основе данных о технологических возможностях, выраженных в коэффициентах прямых затрат: ssp@ugrasu. ru 9

Модель межотраслевого баланса Определение: Модель (2) или матрица А называется продуктивной, если система (2) разрешима в неотрицательных числах при любом 0≤ y. Неразложимость матрицы А означает, что каждая отрасль хотя бы косвенно использует продукцию всех отраслей. ssp@ugrasu. ru 10

Модель межотраслевого баланса Теорема (достаточное условие). Если для неразложимой матрицы прямых затрат сумма элементов для каждой строки не превосходит единицы и хотя бы для одной строки она строго меньше единицы, то модель продуктивна. Замечание. Экономическая интерпретация достаточного условия: продукции каждой отрасли хватает для нужд самого производства, более того есть отрасль, продукция которой остается на потребление ssp@ugrasu. ru 11

Модель межотраслевого баланса Пример. Для вектора потребления найти вектор производства ssp@ugrasu. ru 12

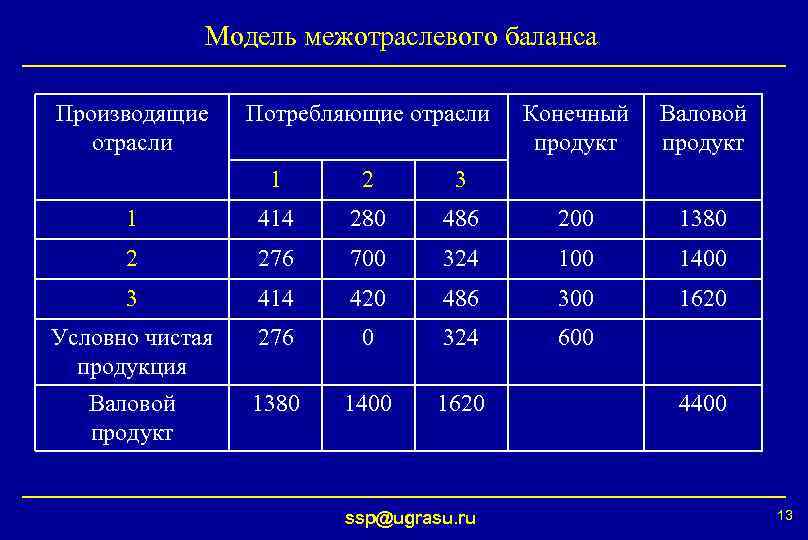Модель межотраслевого баланса Производящие отрасли Потребляющие отрасли Конечный продукт Валовой продукт 1 2 3 1 414 280 486 200 1380 2 276 700 324 100 1400 3 414 420 486 300 1620 Условно чистая продукция 276 0 324 600 Валовой продукт 1380 1400 1620 ssp@ugrasu. ru 4400 13

Модель межотраслевого баланса Систему (3) называют моделью Леонтьева или моделью «затраты-выпуск» ssp@ugrasu. ru 14

Модель межотраслевого баланса § 12. Динамическая модель межотраслевого баланса Рассмотренная ранее модель носила статический характер: ее показатели отнесены к фиксированному (году) промежутку и не зависели от времени в течении этого промежутка. Применим модель для нескольких промежутков, t 1, t 2, …, tk, в каждый год часть вектора конечного продукта y можно пустить на расширение производства ssp@ugrasu. ru 15

Модель межотраслевого баланса Естественно, часть, направляемую на расширение производства, определять в зависимости от прироста валового продукта ssp@ugrasu. ru 16

Модель межотраслевого баланса B – матрица приростных коэффициентов (фондоемкостей) Т. о. , валовой продукт разделяется на три компоненты • производственное потребление • капитальные вложения на расширение производства • конечный продукт Модель (1) называют динамической моделью МОБ, или моделью Неймана ssp@ugrasu. ru 17

Модель межотраслевого баланса ssp@ugrasu. ru 18

Модель межотраслевого баланса Если матрица B приростных фондоемкостей обратима, то получаем динамический баланс Уравнение (2) есть система обыкновенных дифференциальных уравнений от неизвестных функций валовых продуктов отраслей ssp@ugrasu. ru 19

Модель межотраслевого баланса Общее решение системы (2) складывается из общего решения соответствующего однородного уравнения И некоторого частного решения (2) ssp@ugrasu. ru 20

Модель межотраслевого баланса Решение однородного уравнения (3) достаточно хорошо изучено. Решение ОДУ определяется собственными значениями матрицы в правой части системы, т. е. корнями характеристического уравнения: В случае, например, различных корней : ssp@ugrasu. ru 21

Модель межотраслевого баланса Общее решение имеет вид где собственные вектора матрицы отвечающие ssp@ugrasu. ru 22

Модель межотраслевого баланса Для устойчивости экономического показателя x(t) динамического МОБ достаточно, что бы корни характеристического уравнения имели отрицательные действительные части. В этом случае колебания затухают около частного решения в некоторой полосе. Рассмотрим частный случай модели (2). ssp@ugrasu. ru 23

Модель межотраслевого баланса § 13. Модель управления хозяйственной популяцией Рассмотрим одну отрасль, производящей некоторый продукт x(t), например, рыбное хозяйство, или пушной зверь (популяция) Валовый продукт = воспроизводство + конечное потребление ssp@ugrasu. ru 24

Модель межотраслевого баланса Уравнение (2) примет вид Конечным продуктом потребления z(t) можно управлять, и тем самым, влиять на численность популяции x(t) при фиксированных параметрах а и b. Основной вопрос: как влияет природное и искусственное управление z(t) на x(t)? ssp@ugrasu. ru 25

Модель межотраслевого баланса Интересно рассмотреть следующие случаи: 1. z(t)=0 , управления нет 2. z(t)=cx 2 , внутривидовая борьба 3. z(t)=cx 2 +k, управляемый «отлов» ssp@ugrasu. ru 26

Модель развития популяции Рассмотрим несколько другой путь получения той же самой модели Есть мнение, что «Все многообразие мира описывается несколькими моделями» . ssp@ugrasu. ru 27

Модель развития популяции Пусть численность популяции в момент времени. Например, рассматриваем рыбное хозяйство, имеем замкнутый водоем, в который в начальный момент времени запустили рыбу фиксированной породы в количестве x 0. Хотим построить модель, позволяющую прогнозировать динамику изменения количества популяции (рыбы). ssp@ugrasu. ru 28

Модель развития популяции Рассмотрим изменение количества популяции x(t) за промежуток времени [ t, t+Δt] Обозначим Δx = x(t+Δt) – x(t) – прирост популяции за промежуток [ t, t+Δt] Предположим, что прирост Δx прямо пропорционален количеству x(t) с коэффициентом k, т. е. Δx = k∙x(t) Δt ssp@ugrasu. ru 29

Модель развития популяции ssp@ugrasu. ru 30

Модель развития популяции ssp@ugrasu. ru 31

Модель развития популяции ssp@ugrasu. ru 32

Модель развития популяции ssp@ugrasu. ru 33

Модель развития популяции ssp@ugrasu. ru 34

Модель развития популяции ssp@ugrasu. ru 35

Модель развития популяции ssp@ugrasu. ru 36

Модель развития популяции Обозначим: ssp@ugrasu. ru 37

Модель развития популяции Задача (1. 1) примет следующий вид: (2. 1) ssp@ugrasu. ru 38

Модель развития популяции ssp@ugrasu. ru 39

Заменой переменной уравнение можно упростить: ssp@ugrasu. ru 40

Решение: ssp@ugrasu. ru 41

Модель развития популяции Главный вопрос: устойчивость решения ssp@ugrasu. ru 42

Модель развития популяции 1. Решение x=0 устойчиво при a<0 и неустойчиво при a>0. 2. Решение x=1 устойчиво при a>0 и неустойчиво при a<0 ssp@ugrasu. ru 43

a>0 ssp@ugrasu. ru 44

Выводы: Состояние x=1 устойчивое (непроизвольный выход с этой траектории по истечении некоторого времени практически возвращается к x=1); Состояние x=0 неустойчивое (если возникает популяция, то ее численность доходит до 1, в принятом масштабе). Для малых t решение близко к мальтузианскому. ssp@ugrasu. ru 45

Модель межотраслевого баланса Заменой переменной t уравнение можно упростить: ssp@ugrasu. ru 46

Рассмотрим, как скажется численность популяции с постоянной квотой отлова 0

Модель межотраслевого баланса Рассмотрим, как скажется численность популяции с постоянной квотой отлова 0

Модель межотраслевого баланса ssp@ugrasu. ru 49

Модель межотраслевого баланса Ситуация «перелова» , популяция гибнет ssp@ugrasu. ru 50

Модель межотраслевого баланса «Оптимизация, как путь к катастрофе» ssp@ugrasu. ru 51

ssp@ugrasu. ru 52

Модель межотраслевого баланса Контрольные вопросы: 1. Запись модели Леонтьева в координатной и матричной форме 2. Продуктивность матрицы, модели Леонтьева 3. Изолированность множества, неразложимость матрицы 4. Критерии и условия продуктивности матрицы (модели Леонтьева) 5. Схема МОБ 6. Дискретная динамическая модель МОБ 7. Непрерывная динамическая модель МОБ 8. Примеры управления хозяйственной популяцией ssp@ugrasu. ru 53