ЭКОНОМИКА Алгоритмы решения типовых задач Автор презентации

ЭКОНОМИКА Алгоритмы решения типовых задач Автор презентации к. э. н. , доцент кафедры «Национальной экономики» Дальневосточного государственного технического университета (ДВПИ имени В. В. Куйбышева) Чиповская Ирина Степановна

Микроэкономика Тема № 1 Проблема выбора

Задача № 1. 1 На одной лестничной площадке живут соседки Петрова и Максимова. Петрова – квалифицированная портниха, специализирующаяся на пошиве женского платья. Одно платье она шьет в среднем за 20 часов, зарабатывая при этом за каждый час по 80 рублей. Собирается устроить встречу Нового года, сама планирует приготовить праздничный ужин, затратив на его приготовление 10 часов. Максимова – повар. Она работает в кафе, получая 75 рублей в час. Она неплохо шьет и собирается сшить себе платье к Новому году, на пошив планирует затратить 30 часов. На приготовление праздничного ужина у нее уйдет 5 часов. Слайд № 3

Задание: Располагая данной информацией, ответьте на вопрос: Стоит ли Максимовой шить платье, а Петровой – готовить праздничный ужин, если первая не любит шить, а вторая – терпеть не может готовить? Слайд № 4

Решение: Петрова – портниха, готовя праздничный ужин самостоятельно, она потратит 10 часов времени, которое могла бы использовать на шитье платья Максимовой, при этом: 10 часов х 80 рублей = 800 рублей составит потеря в заработке 5 часов х 75 рублей = 375 рублей составит стоимость услуг Максимовой по приготовлению ужина. Слайд № 5

Решение: Максимова – повар, занимаясь шитьем нового платья, она потратит 30 часов времени, которое могла бы использовать на приготовление праздничного ужина Петровой и на другие заказы по профилю, при этом: 30 часов х 75 рублей = 2250 рублей составит потеря в заработке 20 часов х 80 рублей = 1600 рублей составит стоимость услуг Петровой по пошиву платья. Слайд № 6

Вывод: В данном случае, принимая во внимание предпочтения, стоимость услуг и специализацию соседок, выгоднее каждой заниматься тем, в чем они профессионалы. Слайд № 7

Задача № 1. 2 На путешествие самолетом из Москвы в Амстердам менеджер тратит сутки с учетом сопутствующих затрат времени. Поездка на поезде займет двое суток. Авиабилет стоит 300$, а железнодорожный билет – 180 $. Во время передвижения менеджер был лишен возможности зарабатывать. Слайд № 8

Задание: а) Какой способ передвижения дешевле для менеджера, зарабатывающего 150 $ каждый день вне зависимости от того, выходной он или рабочий? б) При каком дневном заработке менеджера ему будет безразличен выбор средства передвижения из Москвы в Амстердам? Слайд № 9

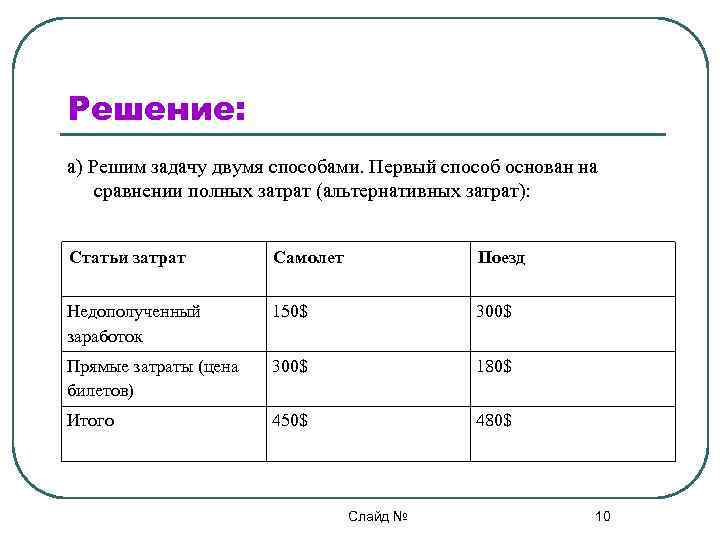Решение: а) Решим задачу двумя способами. Первый способ основан на сравнении полных затрат (альтернативных затрат): Статьи затрат Самолет Поезд Недополученный 150$ 300$ заработок Прямые затраты (цена 300$ 180$ билетов) Итого 450$ 480$ Слайд № 10

Решение: Второй способ принимает во внимание только различия между вариантами Статьи затрат Самолет Поезд Недополученный 0$ 150$ заработок Прямые затраты (цена 300$ 180$ билетв) Итого 300$ 330$ Результат не меняется в зависимости от выбора варианта, авиабилет дешевле на 30$. Слайд № 11

Решение: б) Обозначим через W неизвестный дневной заработок менеджера. Тогда безразличие двух вариантов достигается при 300 +W=180+2 W Откуда находим W=120$. ОТВЕТ: а) авиабилет дешевле на 30$; б) дневной заработок должен быть равен 120$ Слайд № 12

Задача № 1. 3 На путешествие самолетом из Москвы в Красноярск инженер тратит сутки с учетом сопутствующих затрат времени. Поездка в поезде займет 4 дня. Авиабилет стоит 10 тыс. руб, а железнодорожный билет 5800 руб. Сколько должен зарабатывать в будний день инженер (в воскресные дни он не работает), чтобы ему было все равно с чисто экономических позиций – лететь в будний день или ехать поездом 4 будних дня? Слайд № 13

Задача № 1. 4 Программист получил предоплату за заказ в размере 30 тыс. руб. Общая стоимость работы составляет 200 тыс. руб. Она получена исходя из стоимости одного часа работы, равной 1000 руб, и рабочей недели, равной 41 час. Временных ограничений в контракте нет. Наш программист решил посвятить одну неделю ремонту своей квартиры. Чему равна альтернативная стоимость этого решения, если других возможностей, кроме работы над известным заказом и ремонтом в течение длительного времени у него нет? Слайд № 14

Решение С учетом стоимости часа работы недельная загруженность заказом соответствует 41000 руб заработка. Занимаясь ремонтом квартиры, программист на 41 час отодвигает выполнение задания по заказу. С учетом предоплаты альтернативная стоимость выбора будет равна 41000 – 30000 = 11000 руб Слайд № 15

Зачетная самостоятельная задача Семья из трех человек (экономист, его жена и сын) должна выполнять три вида деятельности: работать, вести домашнее хозяйство и делать уроки для сына. Работая, экономист получает 160 руб. в час, жена – 150 руб. в час, сын – 50 руб. в час. Чтобы сделать уроки для сына, экономисту требуется 5, 5 часов в неделю, его жене – 7 часов в неделю, сыну – 17 часов в неделю. Необходимый объем работы по дому экономист может выполнить за 13 часов, жена – за 16 часов, а сын – за 40 часов. Недельный запас времени у экономиста – 60 часов, у его жены – также 60 часов, у сына – 40 часов. Как членам семьи распределить свое время, чтобы доход семьи был максимальным? Слайд № 16

Микроэкономика Тема № 2 Кривая производственных возможностей

Задача № 2. 1 На первом поле фермер может произвести 300 т картофеля или 100 т пшеницы, на втором поле альтернативная стоимость выращивания 1 т пшеницы равна 2 т картофеля при максимальном производстве картофеля – 400 т. Слайд № 18

Задание: а) Какова альтернативная стоимость производства 1 т пшеницы на первом поле? б) Построить кривую производственных возможностей для каждого поля. в) Построить кривую общих производственных возможностей фермера. Слайд № 19

Решение: а) На первом поле, пожертвовав одной тонной пшеницы, фермер высвободил площадь для выращивания трех тонн картофеля. Следовательно, альтернативная стоимость производства 1 т пшеницы на первом поле равна 3 т картофеля. И, наоборот, 1 т картофеля стоит 1/3 т пшеницы (примем условное обозначение 1 П=3 К). Слайд № 20

Решение: б) Построение кривой производственных возможностей показывает, что в нашем случае это прямая, соединяющая точки максимального производства пшеницы и наибольшего производства картофеля. Обозначим на первом поле эти точки следующим образом: (0 П; 300 К) и (100 П; 0 К). Слайд № 21

Решение: Обоснование: Поле можно разделить в любой пропорции. На одной части посеять пшеницу, а на другой картофель. Альтернативная стоимость пшеницы на втором поле выражается следующим соотношением: 1 П=2 К. В результате максимальное производство на этом поле пшеницы равно 200 т (400/2 = 200). Кривая производственных возможностей строится аналогично. Слайд № 22

Решение: в) Построение общей кривой производственных возможностей может вызвать затруднения. Ключом к решению является понятие альтернативной стоимости. Максимум производства пшеницы на двух полях очевиден – это 100+200=300, если засеять оба поля пшеницей. Аналогично можно найти максимум производства картофеля. Таким образом, две точки КПВ мы получили: (300 П; 0 К) и (0 П; 700 К). Слайд № 23

Решение: Далее можно предложить два варианта использования ресурсов. Слайд № 24

Решение: Первый вариант дает верное решение, а второй – нет, т. к. в первом получается выпуклая кривая, а во втором – нет. Но это еще не все. Нужен алгоритм принятия решения. Ведь чем больше у фермера полей, тем больше вариантов для выбора. Слайд № 25

Алгоритм построения общей кривой производственных возможностей: Пусть мы всегда засевали все поля пшеницей, а на следующий год нам потребовалось немного картофеля. На каком поле его посадить? Ясно, что на том, где потери в виде недополученной пшеницы будут минимальными, т. е. там, где альтернативная стоимость картофеля наименьшая. В нашем случае – это первое поле. Если не хватит этого поля, то остаток картофеля надо посадить на поле со следующим по возрастанию значением альтернативной стоимости картофеля и т. д. l Например, ели у фермера три поля, то графически процесс можно иллюстрировать так Слайд № 26

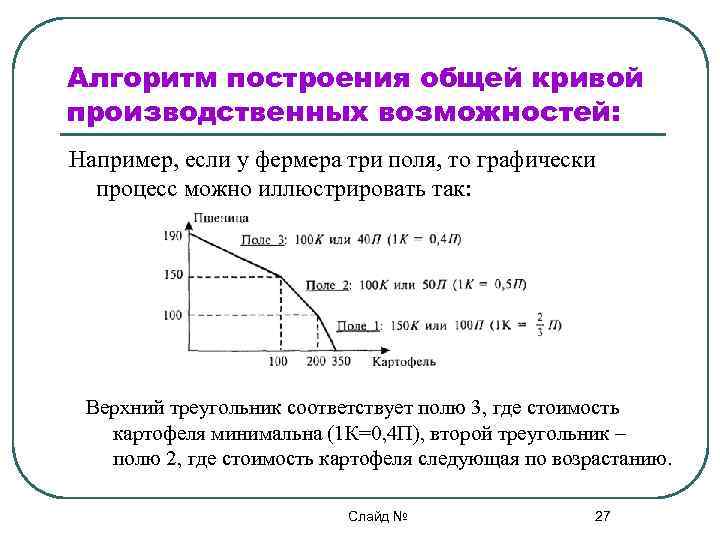Алгоритм построения общей кривой производственных возможностей: Например, если у фермера три поля, то графически процесс можно иллюстрировать так: Верхний треугольник соответствует полю 3, где стоимость картофеля минимальна (1 К=0, 4 П), второй треугольник – полю 2, где стоимость картофеля следующая по возрастанию. Слайд № 27

Задача № 2. 2 Допустим точки А, Б, В, и Г лежат на одной кривой производственных возможностей: А (4000, 11000), Б (8000, 3000), В (7000, Х) и Г (3000, У). Слайд № 28

Задание: Определить полный набор соотношений с участием неизвестных Х и У. Слайд № 29

Решение: Выпуклая форма кривой производственных возможностей и закон возрастающих альтернативных затрат позволяют определить искомые соотношения. Ясно, что Г 3000 У Х<У, 11000<У, 3000<Х, но это еще не все. Прирост производства первого продукта с А 4000 11000 7000 до 8000 был обеспечен большими В 7000 Х потерями второго продукта, чем с 3000 до 4000, т. е. Б 8000 3000 Х – 3000 > У – 11000 Но и это еще не все. Для удобства анализа расположим точки в таблице по возрастанию первой координаты Слайд № 30

Решение: Обратите внимание на расстояние по первой координате между точками В и А. Оно составляет 3000 единиц и в три раза больше, чем расстояние между точками А и Г, а также между точками В и Б. Поэтому Х – 3000 ≥ 1/3 (11000 – Х) ≥ У – 11000 Ответ: У > 11000 > Х > 3000 и Х – 3000 ≥ 1/3 (11000 – Х) ≥ У – 11000 Слайд № 31

Зачетная самостоятельная задача На заводе имеются станки двух типов. Станки первого типа универсальные – их легко можно перенастраивать на производство как деталей вида А, так и деталей вида Б. За смену на одном станке можно изготовить 100 деталей вида А или 200 деталей вида Б. Таких станков на заводе установлено 10. А на станках второго типа можно производить детали только вида Б, однако их производительность в 1, 5 раза больше, чем у станков первого типа. Всего таких станков на заводе 5. В этом году завод закупил 8 новых специализированных станков по производству деталей вида А. Теперь за смену на заводе может производиться деталей вида А в 5 раз больше, чем прежде. а) Покажите на графике, как изменились производственные возможности завода после покупки новых станков. б) Если известно, что на рынке детали можно реализовать только в комплекте: 9 деталей вида А и 5 деталей вида Б, то какое максимальное количество комплектов сможет производить завод за смену? Слайд № 32

Микроэкономика Тема № 3 Теория спроса и предложения

Задача № 3. 1 Рынок некоторого товара представлен следующими функциями спроса и предложения QD=36 -2 P, QS=-4+3 P. Правительство установило на данный товар фиксированную цену в 10 ден. ед. Каков будет объем продаж? Слайд № 34

Решение: При цене в 10 ден. ед. Qсп=36 -2 P = 36 -2∙ 10 =16 Qпр=-4+3 P=-4+3∙ 10 = 26. Ответ: Объем продаж не может быть больше величины спроса, поэтому он будет равен 16 ед. Слайд № 35

Задача № 3. 2 Спрос на товар задается формулой QD=10 -P; предложение данного товара представлено уравнением QS=4 P-5; определите, каким будет абсолютное изменение равновесной цены, если спрос увеличивается на 10%, а предложение – на 20% (в ден. ед. )? Слайд № 36

Решение: Состояние равновесия достигается, когда спрос равен предложению. Поэтому равновесную цену можно определить, приравняв функцию спроса функции предложения. 10 -P=4 P-5 Р=3 ден. ед. Слайд № 37

Решение: Изменение спроса и предложения меняет соответствующим образом их функции. В результате увеличения спроса на 10% функция спроса примет вид: QD=1, 1∙(10 -P)=11 -1, 1 Р Слайд № 38

Решение: В результате увеличения предложения на 20% функция предложения примет вид: QS=1, 2∙(4 P-5)=4, 8 Р-6 Слайд № 39

Решение: Приравняв новую функцию спроса новой функции предложения, находим новую равновесную цену. 11 -1, 1 Р=4, 8 Р-6 Р=2, 88 ден. ед. Ответ: Таким образом, цена снизилась на 0, 12 ден. ед. Слайд № 40

Задача № 3. 3 Рынок некоторого товара характеризовался следующими функциями спроса и предложения: QD=200 -5 P, QS=-50+5 P. Изменившиеся условия рынка привели к тому, что спрос снизился на 20%, а предложение возросло на 30 ед. для каждого уровня цены. Как изменился объем продаж? Слайд № 41

Решение: Состояние равновесия достигается, когда спрос равен предложению. Поэтому равновесную цену можно определить, приравняв функцию спроса функции предложения. 200 -5 P=-50+5 P Р=25 ден. ед. Слайд № 42

Решение: Объем продаж определяем, подставив равновесную цену в функцию спроса либо в функцию предложения. Таким образом, первоначальный объем продаж равен: 200 -5∙ 25=75 ед. Слайд № 43

Решение: Изменение спроса и предложения меняет соответствующим образом их функции. В результате снижения спроса на 20% функция спроса примет вид: QD=0, 8∙(200 -5 P)=160 -4 Р Слайд № 44

Решение: Рост предложения на 30 ед. меняет функцию предложения следующим образом: QS=-50+5 P+30 = -20+5 Р Слайд № 45

Решение: Новое состояние равновесия достигается при условии, что 160 -4 Р=-20+5 Р Р=20 Новый объем продаж будет равен -20+5∙ 20=80. Ответ: Таким образом, объем продаж увеличился на 5 ед. Слайд № 46

Задача № 3. 4 Предложение некоторого товара может быть записано в виде уравнения QS=4 P-100, где Р – цена за единицу товара, ден. ед. Спрос равен 80. В результате совершенствования технологии предложение возрастет на 20 ед. для каждой цены. Определите равновесную цену, при которой будет существовать предложение данного товара после технологических изменений. Слайд № 47

Решение: Изменение спроса и предложения меняет соответствующим образом их функции. Рост предложения на 20 ед. меняет функцию предложения следующим образом: QS=4 P-100+20 = 4 Р-80 Слайд № 48

Решение: Состояние равновесия достигается, когда спрос равен предложению. Поэтому равновесную цену можно определить, приравняв функцию спроса функции предложения. 80=4 Р-80 Р=40 Ответ: Таким образом, равновесная цена, при которой будет существовать предложение данного товара после технологических изменений равна 40 ден. ед. Слайд № 49

Задача № 3. 5 Функции спроса и предложения для некоторого товара имеют вид: QD=100 - P и QS=-20+2 P. Предположим, что результатом неблагоприятной конъюнктуры стало сокращение спроса и предложения для рассматриваемого товара на 50%. Как при этом изменился объем продаж? Слайд № 50

Решение: Состояние равновесия достигается, когда спрос равен предложению. Поэтому равновесную цену можно определить, приравняв функцию спроса функции предложения. 100 -P=-20+2 P Р=40 Слайд № 51

Решение: Объем продаж определяем, подставив равновесную цену в функцию спроса либо в функцию предложения. Таким образом, первоначальный объем продаж равен: 100 -40=60 ед. Слайд № 52

Решение: Изменение спроса и предложения меняет соответствующим образом их функции. В результате снижения спроса на 50% функция спроса примет вид: QD=0, 5∙(100 -P)=50 -0, 5 Р В результате снижения предложения на 50% функция предложения примет вид: QS=0, 5∙(-20+2 P) = -10+Р Слайд № 53

Решение: Новое состояние равновесия достигается при условии, что 50 -0, 5 Р = -10+Р Р=40 Новый объем продаж будет равен -10+40=30. Ответ: Таким образом, объем продаж снизился на 30 ед. Слайд № 54

Задача № 3. 6 Предположим, что при повышении цены на рынке на 2% спрос на товар уменьшился на 5%. Чему равен коэффициент эластичности спроса? Слайд № 55

Решение: Коэффициент эластичности спроса равен: -5% / 2% = -2, 5 Ответ: -2, 5 – мы имеем дело с эластичным спросом. Слайд № 56

Зачетная самостоятельная задача Предложение некоторого товара может быть записано в виде уравнения QS=5 P-120, где Р – цена за единицу товара, ден. ед. Спрос определяется функцией QD=70 -P. В результате совершенствования технологии предложение возрастет на 10 ед. для каждой цены. Определите новый равновесный объем производства. Слайд № 57

Зачетная самостоятельная задача Известно, что при увеличении рыночной цены на 10% производитель увеличил предложение товара на 20%. Чему равен коэффициент эластичности? Слайд № 58

Микроэкономика Тема № 4 Издержки производства и прибыль

Задача № 4. 1 Некий гражданин Н. , отказавшись от должности инженера с окладом 500 долл. в месяц, организовал малое предприятие. Для этого он использовал личные сбережения в сумме 1500 тыс. долл. Кроме того, был привлечен кредит в размере 5000 долл. Какую величину составят экономические и бухгалтерские издержки соответственно, если годовой процент за кредит составляет 20%, а по вкладам граждан – 12% годовых? Слайд № 60

Решение: 1. Бухгалтерские издержки равны =1500 долл. (Личные сбережения) + 5000 долл. (Кредит) + 1000 долл (20% от 5000 долл. за кредит) = 7500 долл. 2. Экономические издержки = бухгалтерские издержки + вмененные издержки = 7500 + (500 долл*12 мес. =6000 Оклад инженера за год) +180 долл. (12% от личных сбережений, равных 1500 долл. ) = 13680 долл. Слайд № 61

Задача № 4. 2 Мистер Скрудж владеет небольшой фирмой по производству керамики. Он нанимает одного помощника за 12 тыс. долл. В год с оплатой в конце года, и 20 тыс. долл. В год уходит на покупку сырья и материалов с оплатой в начале года. В начале года для приобретения нового оборудования, срок эксплуатации которого составляет 8 лет, мистер Скрудж взял в банке кредит в размере 40 тыс. долл. Под 10% годовых с возвратом суммы кредита и процентов в конце года. Процент по депозиту равен 7. Мистер Скрудж использует собственное помещение под мастерскую. Он мог бы сдавать его в аренду за 10 тыс. долл. в год с оплатой в конце года. Конкурент мистера Скруджа предлагает ему рабочее место гончара с зарплатой 15 тыс. долл. в год с условием выплаты этой суммы в конце года. Суммарный годовой доход от продажи керамических изделий составляет 65 тыс. долл. Найти годовую бухгалтерскую и экономическую прибыль мистера Скруджа. Слайд № 62

Решение: Запишем в таблице явные и неявные издержки: Явные издержки, тыс. долл. Неявные издержки, тыс. долл. 1. Зарплата помощника 12 1. Неполученный процент 20 х 0, 07 2. Затраты на сырье 20 2. Неполученная зарплата 15 3. Неполученная арендная 3. Процент 40 х 0, 1 10 плата 4. Амортизация 40 х 0, 125 Всего: 41 Всего: 26, 4 Итого: экономические издержки составляют 67, 4 тыс. долл. Слайд № 63

Решение: Бухгалтерская прибыль = 65 - 41 = 24 тыс. долл. Экономическая прибыль = 65 - 67, 4 = -2, 4 тыс. долл. Ответ: 24 и -2, 4 тыс. долл. Слайд № 64

Задача № 4. 1 Ориентировочная цена будущей книги – 10 ден. ед. Совокупные постоянные издержки на издание данной книги – 200000 ден. ед. Совокупные переменные издержки на один экземпляр данной книги – 6 ден. ед. Рассчитать, при каком тираже издание книги будет безубыточным. Слайд № 65

Решение: Р = 10 ден. ед. FC = 200000 ден. ед. AVC = 6 ден. ед. P = ATC = FC/Q + AVC 10 = 200000/Q + 6 Q = 200000/4 = 50000 шт. Ответ: 50000 шт. Слайд № 66

Задача № 4. 2 На основе данных таблицы рассчитать себестоимость, средние постоянные и средние переменные издержки предприятия Выпуск продукции 0 1000 2000 3000 4000 5000 6000 7000 в единицу времени, шт. Общие затраты, 1000 1400 1800 2200 2600 3000 3400 3800 ден. ед. Слайд № 67

Решение: FC = TC при Q = 0 FC = 1000 ден. ед. AFC = FC/Q VC = TC – FC AVC = VC/Q АТС - 1, 4 0, 9 0, 7 0, 65 0, 6 0, 55 0, 54 (с/с) AFC 1000 1 0, 5 0, 33 0, 25 0, 2 0, 17 0, 14 VC - 400 800 1200 1600 2000 2400 2800 AVC - 0, 4 0, 4 Слайд № 68

Задача № 4. 3 Функционирование условного предприятия в предыдущем квартале характеризовалось следующими показателями: общие постоянные издержки – 15000 ден. ед. ; средние переменные издержки – 10 ден. ед. ; цена за единицу продукции – 20 ден. ед. ; валовая прибыль – 5000 ден. ед. Прогнозируя наступление спада в экономике страны, руководство фирмы принимает решение о снижении постоянных издержек на 20% при одновременном сохранении объема производства и доли прибыли. Определить новую цену продукции. Слайд № 69

Решение: FC 1 = 15000 AVC = 10 G = 5000 P 1 = 20 P = FC/Q + AVC + G/Q 20 = 15000/Q + 10 + 5000/Q 20 Q = 15000 + 10 Q + 5000 Q = 20000/10 = 2000 FC 2 = 0, 8 FC 1 = 0, 8 x 15000 = 12000 P 2 = 12000/2000 + 10 + 5000/2000 P 2 = 6 + 10 + 2, 5 = 18, 5 Ответ: 18, 5 ден. ед. Слайд № 70

Задача № 4. 4 Работа предприятия за истекший период характеризовалась следующими показателями: AVC=20 ден. ед. , AFC=10 ден. ед. , Q=1000 шт. , G (прибыль)=5000 ден. ед. Определите цену (Р) реализации продукции. Слайд № 71

Решение: Прибыль получаем, вычитая из выручки от реализации продукции совокупные издержки. Совокупные издержки равны сумме постоянных и переменных издержек. То же самое верно и для средних величин. Поэтому Прибыль на единицу продукции = Р – (AVC + AFC) Слайд № 72

Решение: Следовательно, Р = Прибыль на единицу продукции + (AVC + AFC) Р = 5000/1000 + 20 + 10 = 35 Ответ: Таким образом, цена реализации продукции равна 35 ден. ед. Слайд № 73

Задача № 4. 5 Предприятие, выпустив 50 изделий, имело следующие издержки: постоянные – 200 д. е. , средние валовые – 60 д. е. Чему равны средние переменные издержки? Слайд № 74

Решение: AVC= AТC- AFC= FC/ Q AVC=60 -200/50=56 Ответ: 56 ден. ед. Слайд № 75

Задача № 4. 6 Производственные мощности предприятия позволяют выпустить за год 20000 изделий при постоянных общих издержках 30 млн. д. е. Максимально возможная цена единицы продукции, по которой может быть полностью реализован такой объем выпуска, составляет 3000 д. е. Руководство предприятия поставило перед собой цель получить 10 млн. д. е. прибыли в год. Какими должны быть средние переменные издержки? Слайд № 76

Решение: Прибыль получаем, вычитая из выручки от реализации продукции совокупные издержки. Совокупные издержки равны сумме постоянных и переменных издержек. 10 млн. д. е. = 20000 х3000 д. е. – (30 млн. д. е. + VC) Слайд № 77

Решение: Следовательно, переменные издержки равны VC = 20 млн. д. е. AVC=20 млн. д. е. /20000 = 1000 д. е. Ответ: 1000 д. е. Слайд № 78

Задача № 4. 7 Работа предприятия в предыдущем году характеризовалась следующими показателями: объем выпуска – 2500 шт. ; общие постоянные издержки – 4000 д. е. ; цена за единицу продукции – 5 д. е. ; средние переменные издержки – 3 д. е. В связи с ожидаемым экономическим спадом предприятие в планируемом отрезке времени должно снизить объем выпуска на 20%. На сколько процентов должны быть снижены постоянные издержки, если предприятие предполагает получить такой же объем прибыли, как и в предыдущем году? Слайд № 79

Решение: Постоянные издержки предыдущего года находим, исходя из того, что прибыль равна разнице между выручкой от реализации продукции и совокупными издержками, а совокупные издержки равны сумме постоянных и переменных издержек. Поэтому: Прибыль = 2500∙ 5 – (4000+2500∙ 3) Прибыль = 1000 Слайд № 80

Решение: Снижение объема выпуска на 20% сделает его равным 2000 шт. Если предприятие желает сохранить прежний объем прибыли в 1000 д. е. , его постоянные издержки должны быть равны 1000 = 2000∙ 5 – (FC+2000∙ 3) FC = 3000 Ответ: Таким образом, постоянные издержки необходимо снизить на 1000 д. е. , или на 25%. Слайд № 81

Задача № 4. 8 Результаты функционирования предприятия в прошедшем году характеризовались следующими показателями: выручка – 16500 д. е. ; общие переменные издержки – 13800 д. е. ; общие постоянные издержки – 2300 д. е. В текущем году ожидается снижение за счет объема производства выручки на 10%. Насколько должны быть сокращены общие переменные издержки в текущем году, чтобы его прибыль осталась на уровне прошлого года? Слайд № 82

Решение: Прибыль получаем, вычитая из выручки от реализации продукции совокупные издержки. Совокупные издержки равны сумме постоянных и переменных издержек. Поэтому Прибыль = 16500 -(13800+2300) = 400 Слайд № 83

Решение: Снижение объема выпуска на 10% уменьшит выручку до 14850 д. е. Если предприятие желает сохранить прежний объем прибыли в 1000 д. е. , его постоянные издержки должны быть равны 400 = 14850 – (VC +2300) VC = 12150 Ответ: Таким образом, переменные издержки необходимо снизить на 1650 д. е. Слайд № 84

Задача № 4. 9 Производство продукции на предприятии характеризовалось следующими параметрами: общие постоянные издержки – 20 млн. д. е. ; средние переменные издержки – 6 тыс. д. е. ; цена за единицу продукции – 12 тыс. д. е. ; объем производства – 6 тыс. шт. С учетом благоприятной конъюнктуры фирме удалось увеличить объем производства на 20% при тех же постоянных издержках. Насколько при этом возросла прибыль? Слайд № 85

Решение: Первоначальную прибыль находим, исходя из того, что она равна разнице между выручкой от реализации продукции и совокупными издержками, а совокупные издержки равны сумме постоянных и переменных издержек. Поэтому Прибыль = 12 тыс. д. е. ∙ 6 тыс. – (20 млн. д. е. + 6 тыс. д. е. ∙ 6 тыс. ) Прибыль =16 млн. д. е. Слайд № 86

Решение: Увеличение объема выпуска на 20% сделает его равным 7200 шт. С учетом благоприятной конъюнктуры прибыль увеличилась и составила Прибыль = 12 тыс. д. е. ∙ 7, 2 тыс. – (20 млн. д. е. + 6 тыс. д. е. ∙ 7, 2 тыс. ) Прибыль =23, 2 млн. д. е. Ответ: Таким образом, прибыль увеличилась на 7, 2 млн. д. е. , или на 45%. Слайд № 87

Зачетная самостоятельная задача Розничные торговцы купили на мелкооптовом рынке по 100 кг бананов по цене 4 р. за килограмм. В течение дня они продавали бананы по цене 6 р. за килограмм. К концу торгового дня бананы начали портиться. У каждого продавца из 100 кг осталось 30 кг. Первый продавец начал сбрасывать цену и только при цене 3 р. продал оставшиеся бананы. Второй продавец решил, что это не выгодно и держал цену на уровне 6 р. , оставшиеся бананы у него сгнили. Слайд № 88

Задание: 1. В чем причина ошибки второго продавца? 2. Найти бухгалтерскую и экономическую прибыль первого продавца, если торговое место стоит 40 р. в день, а альтернативный заработок продавца в лучшем случае составляет 80 р. в день. 3. Рационально ли действовал первый продавец? Слайд № 89

Зачетная самостоятельная задача Рассчитайте по таблице издержки: постоянные (FC), переменные (VC), предельные (MC), средние общие (ATC), средние постоянные (AFC), средние переменные (AVC). Слайд № 90

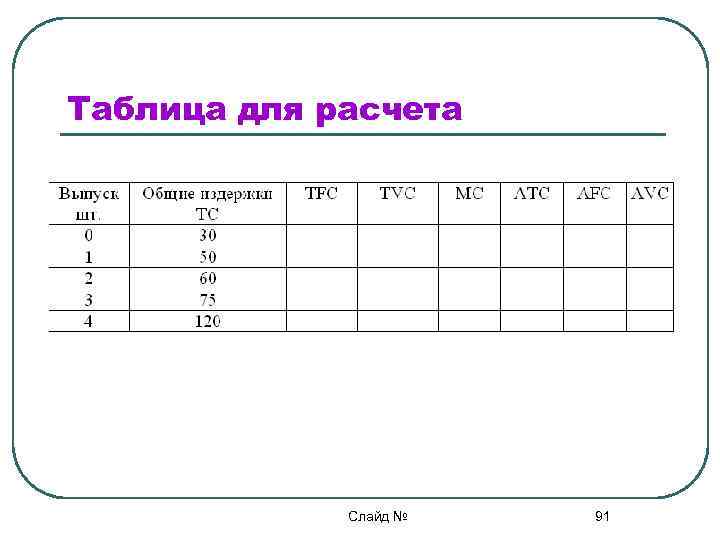Таблица для расчета Слайд № 91

Микроэкономика Тема № 5 Производительность

Задача № 5. 1 Две компании «Юниор» и «Звезда» производят торты «Москвичка» . «Юниор» выпекает за неделю 400 тортов при 4 -х часовом рабочем дне силами 5 человек, работающих 5 дней в неделю. 25 работающих в АО «Звезда» производят значительно больше: 700 тортов при 8 часовом рабочем дне все 7 дней в неделю. Слайд № 93

Задание: Вычислить производительность труда в обеих фирмах за рабочую неделю, день, час. Слайд № 94

Решение: Компания «Юниор» силами 5 рабочих производит в неделю 400 тортов при рабочем времени в 20 ч. Производительность 400 тортов = 4 торта в час труда 5 чел. х 20 ч/чел. Остальные показатели определяются аналогично. Результаты расчетов производительности труда (тортов в единицу времени, производимых в расчете на одного работника) свести в таблицу. Фирма «Юниор» «Звезда» В неделю В день В час 4 Слайд № 95

Ответ: Фирма «Юниор» «Звезда» В неделю 80 280 В день 16 40 В час 4 5 Слайд № 96

Задача № 5. 2 Допустим, компания «Юниор» привлекла еще 3 рабочих для выпечки 360 пирожных в день. Как определить производительность труда и трудоемкость? Слайд № 97

Решение: В натуральном выражении вычислить производительность нельзя, так как никто не знает, как складывать торты и пирожные. Предположим, что в час 8 работников производят 20 тортов и 90 пирожных. Если цена торта составляет 51 р. , а пирожного – 10 р. , то: Производительность 20 х 51 + 90 х 10 = 240 р. /ч. труда 8 Внимание! Производительность измеряется не затратами на производство, а рыночными ценами произведенных товаров и услуг. Трудоемкость составит 1/2, 4 ч, или 25 мин потребуется на выпуск продукции на 1 р. Слайд № 98

Ответ: Производительность труда: 240 р/ч; Трудоемкость: 25 мин потребуется на выпуск продукции на 1 р. Слайд № 99

Задача № 5. 3 В первый год производительность труда на предприятии выросла на 10%, во второй – еще на 20%, а в третьем году производительность снизилась на 5%. На сколько процентов увеличилась или уменьшилась годовая производительность труда в течении этих 3 лет? Слайд № 100

Решение: Применим к решению данной задачи индексную технику: Темп прироста производительности труда, равный 10%, означает увеличение производительности труда в 1, 1 раза; 20% - это увеличение в 1, 2 раза той производительности труда, которая за предыдущий год уже увеличилась в 1, 1 раза; Снижение производительности труда на 5% соответствует индексу, равному 0, 95. Значит, за 3 года производительность труда увеличилась в: 1, 1 х 1, 2 х 0, 95 = 1, 254 раза, или на 25, 4% Слайд № 101

Задача № 5. 4 Рабочий день уменьшился с 8 до 7 ч. На сколько процентов повысилась производительность труда, если при тех же расценках сдельная заработная плата выросла на 5%? Слайд № 102

Задача № 5. 5 Рабочий день уменьшился с 8 до 6 ч. На сколько процентов повысилась производительность труда, если при тех же расценках сдельная заработная плата выросла на 2%? Слайд № 103

Зачетная самостоятельная задача В повестке дня общего собрания компании Я стоит вопрос об открытии нового зарубежного филиала по сборке автомобилей. Специалистами компании были разработаны 2 альтернативных бизнес- плана. Планом А предусмотрено создание филиала в стране Х, а планом Б – в стране Y. Слайд № 104

Задание: Можно ли, на основании информации, представленной в таблице, определить: Какой план будет более выгоден компании? В какой стране производительность труда выше? На сколько процентов? Часовая Цена 1 Стран Денежная производительнос автомобиля, (в а единица (ДЕ) ть 1 работника, (в ДЕ страны) Х Иксики 400 5 Y Игреки 16 000 250 Курс обмена валют 1 иксик = 30 игрекам Слайд № 105

Макроэкономика Тема № 1 Основные макроэкономические показатели и их измерение

Задача № 1. 1 Компания по производству шин продает фирме, производящей автомобили, 4 шины стоимостью 400 долл. Другая автомобильная компания продает автомобильной фирме плеер за 500 долл. Установив все это на новой машине, автомобильная фирма продает ее за 20000 долл. Какая сумма будет включена при подсчете в состав ВВП? Слайд № 107

Решение: При расчете ВВП в его состав будет включена сумма расходов на Ответ: приобретение машины, т. е. 20000 ден. ед. Слайд № 108

Задача № 1. 2 Номинальный ВВП равен 2800 д. е. , дефлятор – 160%. Какова величина реального ВВП? Слайд № 109

Решение: Реальный ВВП = Номинальный ВВП / Дефлятор (в долях единицы) Ответ: Реальный ВВП = 2800 д. е. / 1, 6 = 1750 ден. ед. Слайд № 110

Задача № 1. 3 Определите объем ВНП по следующим данным (ден. ед. ) заработная плата 35000 закупки правительства 5000 импорт 3000 косвенные налоги 3000 процент 210 рентные платежи 7100 экспорт 4000 потребительские расходы 40000 инвестиции 5000 Слайд № 111

Решение: ВНП = С + I + G + Xn Где: C – личные потребительские расходы; I – валовые инвестиции; G – государственные закупки товаров и услуг; Xn – чистый экспорт (экспорт – импорт). ВНП = 40000 + 5000 + 1000 = 51000 (ден. ед. ). Ответ: 51000 ден. ед. Слайд № 112

Задача № 1. 4 Определите объем ВНП по следующим данным (ден. ед. ): импорт 1200; амортизационные отчисления 300; экспорт 1400; заработная плата 8100; процент 200; рента 500; инвестиции 200; косвенные налоги 700; прибыль 1800. Слайд № 113

Решение: ВНП = Z + R + K + P + A + Nб Где: Z - вознаграждение за труд; R – рента; K – процент; P – прибыль; A – амортизационные отчисления; Nб – косвенные налоги. ВНП = 8100 + 500 + 200 + 1800 + 300 + 700 = 11600 (ден. ед. ). Ответ: 11600 ден. ед. Слайд № 114

Макроэкономика Тема № 2 Макроэкономическое равновесие

Задача № 2. 1 В году (t-1) потенциальный ВНП составил 4000, кривая AD описывалась уравнением Y=4200 -2 P. В году t потенциальный ВНП вырос на 1%, а уравнение совокупного спроса приняло вид Y=4280 -2 P. На сколько процентов изменился равновесный уровень цен в году t Слайд № 116

Решение: В году (t-1) уровень цен можно определить как: 4000 = 4200 -2 Р Р=100 В году t уровень цен можно определить как: 4040 = 4280 -2 Р Р=120 Ответ: Следовательно, уровень цен вырос на 20%. Слайд № 117

Макроэкономика Тема № 5 Безработица. Инфляция

Задача № 5. 1 Предположим, Вы заключили трудовое соглашение на выполнение в течение месяца определенного объема работ общей стоимостью 4000 д. е. Определите Ваши абсолютные потери, обусловленные тем, что в условиях 50%-ной инфляции в месяц расчет за выполненные работы осуществляется не в начале, а в конце месяца. Слайд № 119

Решение: Сумма, полученная по трудовому соглашению, в реальном выражении корректируется на темпы инфляции. Она будет равна 4000 д. е. / 1, 5 = 2667 д. е. Следовательно, абсолютные потери, обусловленные тем, что в условиях 50%-ной инфляции в месяц расчет за выполненные работы осуществляется не в начале, а в конце месяца, составят Ответ: 4000 д. е. - 2667 д. е. = 1333 д. е. Слайд № 120

Задача № 5. 2 Определите, во сколько раз в течение года обесценятся 10000 д. е. , хранящихся в банке под 80% годовых, если темп инфляции в стране составляет 20% в месяц. Слайд № 121

Решение: В номинальном выражении 10000 д. е. , хранящихся в банке под 80% годовых, к концу года превратятся в 10000 д. е. + 80%∙ 10000 д. е. = 18000 д. е. Слайд № 122

Решение: Однако инфляция обесценивает средства, хранящиеся в банке, в соответствии с темпами инфляции. Поэтому в реальном выражении 10000 д. е. , хранящихся в банке под 80% годовых, к концу года превратятся в 18000 д. е. / (1, 2)12=2019 д. е. Ответ: Следовательно, в течение года 10000 д. е. , хранящихся в банке под 80% годовых, обесценятся приблизительно в 5 раз. Слайд № 123

Задача № 5. 3 Цена купленной Вами недвижимости за 5 лет возросла на 550%, а инфляция за те же 5 лет по годам составила: 40%; 30%; 15%. Каков индекс реальной стоимости купленной Вами недвижимости? Слайд № 124

Решение: За 5 лет цены возросли в соответствии с ежегодными темпами инфляции. В разах этот рост составил 1, 4∙ 1, 3∙ 1, 15 = 3, 8 Слайд № 125

Решение: Индекс реальной стоимости купленной недвижимости = Индекс роста стоимости недвижимости / Темпы инфляции (в долях единицы) Ответ: Индекс реальной стоимости купленной недвижимости = 6, 5/3, 8 = 1, 7. Слайд № 126

Задача № 5. 4 Вы одолжили 1000 д. е. в условиях 12%- ной инфляции в год и хотите ровно через год получить реальные 1050 д. е. Определите, какую процентную ставку с учетом инфляции Вы должны назначить для этого. Слайд № 127

Решение: В номинальном выражении сумма, подлежащая возврату, должна быть равна 1050 д. е. ∙ 1, 12 = 1176 д. е. Следовательно, процентный доход равен 1176 д. е. - 1100 д. е. = 176 д. е. Уровень процентной ставки равен Ответ: (176 д. е. /1000 д. е. )∙ 100% = 17, 6% Слайд № 128

Макроэкономика Тема № 6 Рынки факторов производства Слайд №

Задача № 6. 1 Как предельная доходность труда рождает спрос на него. В ООО «Матрешка, представляющем собой мастерскую по изготовлению матрешек, месячный выпуск зависит только от количества мастеров. Вопрос первый: Допустим, зарплата мастера составляет в месяц 1600 руб. Какова величина спроса на труд мастеров по изготовлению матрешек со стороны мастерской при отпускной цене матрешки, равной 10 руб? Вопрос второй: Как построить шкалу спроса данной мастерской на труд? Слайд № 130

Решение: 1. Фактически требуется найти число работников, при котором достигается максимум прибыли, если зарплата мастера составляет 1600 руб, а отпускная цена, т. е. оптовая цена по которой ООО продает матрешки оптовым торговцам, равна 10 руб. Применим маржинальный анализ: Количество работников 1 2 3 4 5 6 Месячный выпуск, шт 200 480 801 1000 1150 1315 Прирост выручки, руб 2000 2800 3210 1990 1500 1650 Прирост расходов на оплату 1600 1600 труда, руб Прирост прибыли, руб 400 1200 1610 390 -100 50 Слайд № 131

Решение: 1. Будем гипотетически увеличивать число работников до тех пор, пока прирост выручки при найме дополнительного работника превышает прирост расходов на оплату труда. Таким образом, оптимальное количество работников равно 4. Данная задача интересна тем, что немного нарушен принцип убывающей предельной отдачи (это вполне возможно), поэтому следует рассмотреть также возможность найма 6 рабочих. Прирост выручки при найме с 4 до 6 рабочих составляет 3160 руб, а прирост издержек - 3200 руб. Следовательно, в лучшем случае нужно нанять 4 рабочих, и это означает, что при зарплате равной 1600 руб, величина спроса на труд со стороны ООО «Матрешка» составит 4 работника в месяц. Слайд № 132

Решение: 2. Шкала спроса представляет собой таблицу заданной зависимости величины спроса от цены. Шкала спроса будет специфической. Некоторым целым числам из интервала (0; 6) не найдется места в шкале в качестве величины спроса на труд. Если пропущенное число равно N, то это означает, что ни при какой зарплате не будет выгодным нанимать именно N мастеров. На восходящей части кривой маржинальной выручки этот разрыв «запланирован» . Например, одного работника невыгодно нанимать ни при каких значениях зарплаты. Слайд № 133

Решение: 2. Действительно, можно было бы нанять одного работника при зарплате меньшей, чем прирост выручки, который дает первый работник, т. е. 2000 руб. Но второй работник принесет значительно больше – еще 2800 руб. Таким образом, два работника всегда лучше, чем один. Аналогично получаем, что и двух работников невыгодно нанимать ни при какой зарплате. Так будет продолжаться, пока кривая предельной выручки от дополнительной единицы труда не достигнет своего максимума. В данном случае это произойдет в точке L = 3, т. е. при найме трех работников. Трех мастеров будет выгодно нанимать, если их суммарная оплата труда будет меньше, чем общая выручка, или, что одно и то же, ставка заработной платы будет меньше средней выручки. Поэтому при ставке заработной платы свыше 8010/3 = 2670 руб в месяц, рабочих мест нет, а при 2660 руб – сразу три. Слайд № 134

Решение: 2. С ростом количества труда, вовлеченного в производство, величина предельной выручки рано или поздно начинает убывать. Происходит это в силу закона убывающей предельной отдачи факторов производства. Держать только трех работников следует, если зарплата будет превышать маржинальную отдачу четвертого работника, т. е. 1990 руб. Четвертого работника еще будет целесообразно нанять, если зарплата будет меньше 1990 руб, но больше того предела, при котором выгоднее будет нанять больше мастеров. Поскольку при переходе от точки L = 5 к точке L = 6 опять наблюдается небольшой рост маржинальной отдачи, то пять работников не нужно нанимать ни при какой оплате труда. Это нетипично, но возможно. Именно это создает дополнительную сложность при решении данной задачи. Слайд № 135

Решение: 2. Для ответа на поставленный вопрос следует рассмотреть возможность нанять 6 рабочих. Так как прирост выручки при найме с 4 до 6 рабочих составляет 3350 руб, то при зарплате, меньшей чем: 3350 / (6 -4) = 1675 руб, стоит нанимать максимально возможное количество – 6 мастеров. А при зарплате от 1675 до 1990 руб, в лучшем случае надо нанять 4 рабочих. В результате получаем такую шкалу спроса: Зарплата, руб. от 0 до 1675 от 1675 до 1990 от 1990 до 2670 Величина 6 4 3 0 спроса Слайд № 136

Задача № 6. 2 Рынок труда является конкурентным. Производственная функция фирмы, являющейся совершенным конкурентом на рынке готовой продукции, в краткосрочном периоде имеет вид: Q = 60 L 0, 5 , где L – количество работников. Цена готовой продукции – 5 долл. , а уровень заработной платы – 10 долл. Сколько работников наймет фирма, максимизирующая свою прибыль? Слайд № 137

Решение: MPL = (60 L 0, 5 )’ = 30/ ; MRPL = P x MPL = 5 x 30/ = W = 10. Отсюда L = 225. Слайд № 138

Зачетная самостоятельная задача Допустим, что на нижегородском рынке неквалифицированной рабочей силы кривая спроса на труд выражается зависимостью Ld = 900 – 2 W, А предложение труда неэластично: LS = 300, где W – месячная оплата труда в рублях, Ld и LS - величины спроса и предложения в тысячах человек в год Слайд № 139

Задание: 1. Выяснить, как изменится занятость на этом рынке, если нижегородский губернатор введет минимальную оплату труда на уровне 400 р. ? Возникнет ли дефицит рабочей силы? 2. Что произойдет на этом рынке в результате уменьшения минимальной оплаты труда до 300 р. ? Слайд № 140

Макроэкономика Тема № 6 Денежно-кредитная система

Задача № 6. 1 Предположим, что норма обязательных резервов равна 15%. Величина депозитов коммерческого банка составляет 15000. Банк может выдать ссуды объемом не более 12150. Каковы избыточные резервы банка в процентах от депозитов? Слайд № 142

Решение: Обязательные резервы = 0, 15∙ 15000=2250 Избыточные резервы = 15000 -12150 - 2250 = 600. Ответ: В процентах от депозитов они равны (600/15000)*100% = 4% Слайд № 143

Задача № 6. 2 Норма резервов равна 10%. С помощью операций на открытом рынке Центральный Банк может увеличить предложение денег максимум на 500 млрд. руб. На какую сумму в этом случае он должен выкупить облигации? Слайд № 144

Решение: Покупая облигации, Центральный Банк увеличивает резервы коммерческих банков и расширяет денежное предложение на 500 млрд. руб. Сумма выкупленных облигаций составит: 500 млрд. руб. ∙ 0, 1 = 50 млрд. руб. Ответ: 50 млрд. руб. Слайд № 145

Задача № 6. 3 Норма резервов равна 0, 25. С помощью операций на открытом рынке Центральный Банк может увеличить предложение денег максимум на 440 млрд. руб. На какую сумму в этом случае он должен выкупить облигации? Слайд № 146

Решение: Покупая облигации, Центральный Банк увеличивает резервы коммерческих банков и расширяет денежное предложение на 440 млрд. руб. Сумма выкупленных облигаций составит: 440 млрд. руб. ∙ 0, 25 = 110 млрд. руб. Ответ: 110 млрд. руб. Слайд № 147

Задача № 6. 4 Деньги совершают 5 оборотов в год и объем безналичных платежей равен нулю. Определить количество денег, необходимых для обращения, относительно ВНП. Слайд № 148

Решение: PQ = MV ВНП = PQ ВНП = MV ВНП = М х 5 М = 1/5 ВНП = 0, 2 ВНП Ответ: количество денег, необходимое для обращения составляет 0, 2 ВНП. Слайд № 149

Задача № 6. 5 Если кол-во денег равно 2500 ден. ед. , сумма цен товаров равна 13500 ден. ед. , скорость обращения денег составляет 3 оборота, определить, какова величина безналичных платежей в экономике. Слайд № 150

Решение: PQ = MV Σ PQ – сумма цен товаров 13500 = 2500 х 3 + Х Х = 6000 ден. ед. Ответ: сумма безналичных платежей составит 6000 ден. ед. Слайд № 151

Задача № 6. 6 По данным таблицы определить физический объем производства в текущем году если скорость обращения осталась неизменной Показатели Предыдущий год Текущий год Предложение денег 250 300 Физический объем 100 производства Уровень цен 10 15 Слайд № 152

Решение: P 1 Q 1 = M 1 V 1 10 х 100 = 250 х V 1 = 1000/250 = 4 P 2 Q 2 = M 2 V 1 15 х Q 2 = 300 х 4 Q 2 = 1200/15 = 80 Ответ: 80 ед. Слайд № 153

Задача № 6. 7 Допустим, реальный (физический) объем ВНП увеличился в 1, 2 раза, а денежная масса возросла на 8%. Определить, как изменится уровень цен при стабильной скорости обращения денег. Слайд № 154

Решение: P 1 Q 1 = ВНП 1 = M 1 V 1 ВНП 2 = 1, 2 х ВНП 1 M 2 = 1, 08 М 1 = 300 х 4 V 1 = V 2 Ответ: 80 ед. Слайд № 155