Эконометрика Семинар 6 Ранговая корреляция Для измерения

Эконометрика Семинар 6

Ранговая корреляция Для измерения тесноты связи в случае изучения неколичественных признаков с непрерывными или неизвестными законами распределения применяются методы непараметрической статистики, среди которых наиболее распространены методы ранговой корреляции.

Основные понятия Вариационный ряд для признака x Ранг – номер наблюдения в вариационном ряду Например, суммы баллов, набранные студентами за 5 коллоквиумов были следующими: 40 43 34 10 21 35 8 20 43 8 Вариационный ряд: 43 43 40 35 Задание: присвоить ранги 34 21 20 10 8 8

Коэффициент ранговой корреляции Спирмэна Коэффициент ранговой корреляции Спирмэна вычисляется по формуле: Коэффициент Спирмэна находится в диапазоне: Коэффициент ранговой корреляции Спирмэна должен быть дополнен проверкой значимости!

Проверка значимости для малой выборки (n≤ 30) Полученное расчетное значение коэффициента ранговой корреляции Спирмэна сравнивается с табличным значением. Если , коэффициент значим на определенном уровне значимости α, и наоборот.

Проверка значимости для больших выборок Рассчитывается статистика Стьюдента по формуле: Расчетное значение t-статистики сравнивается с табличным значением t-статистики с (n-2) степенями свободы на уровне значимости α: ◦ Если , коэффициент ранговой корреляции Спирмэна значим на соответствующем уровне α; ◦ Если , коэффициент не значим на соответствующем уровне α

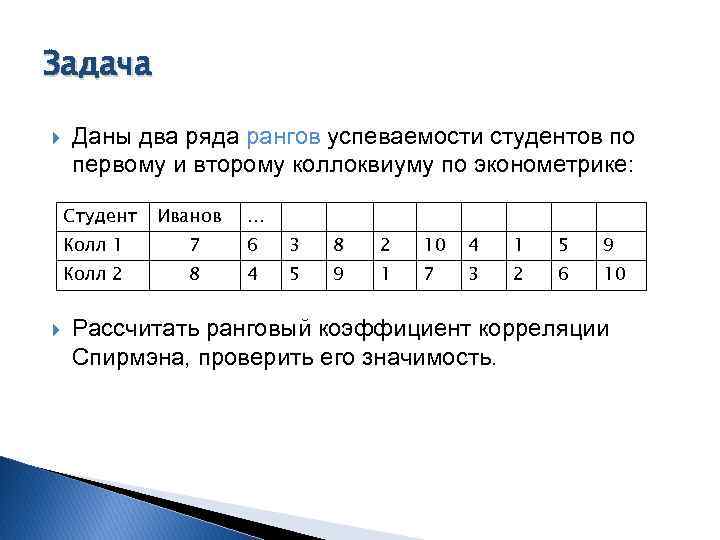Задача Даны два ряда рангов успеваемости студентов по первому и второму коллоквиуму по эконометрике: Студент Иванов … Колл 1 6 3 8 2 10 4 1 5 9 Колл 2 7 8 4 5 9 1 7 3 2 6 10 Рассчитать ранговый коэффициент корреляции Спирмэна, проверить его значимость.

Решение Рассчитаем D и Студент Иванов в таблице: … Колл 1 7 6 3 8 2 10 4 1 5 9 Колл 2 8 4 5 9 1 7 3 2 6 10 -1 2 -2 -1 1 3 1 -1 -1 -1 1 4 4 1 1 9 1 1 D Табличные значения:

Коэффициент ранговой корреляции Кэндалла Вся необходимая информация представлена в дополнительном материале!