ЭКОНОМЕТРИКА Лекция Статистические процедуры оценки параметров линейных моделей

ЭКОНОМЕТРИКА Лекция. Статистические процедуры оценки параметров линейных моделей

Свойства оценок Несмещенность. Совпадение математического ожидания оценки параметра с его истинным значением Эффективность. Оценка считается эффективной, если она имеет минимальную дисперсию среди других оценок того же параметра Состоятельность. Оценка считается состоятельной, если свойство несмещенности выполняется при неограниченном увеличении объема выборки

Выборка и ее свойства Определение. Выборка – это случайный вектор, составленный из результатов наблюдений, каждое из которых суть независимая случайная величина Пусть y 1, y 2, …, yn результаты наблюдения за поведением случайной величины Y c законом распределения Py(t, A) Тогда выборка есть вектор, собранный из результатов наблюдений Y=(y 1, y 2, …, yn)T Каждый элемент выборки есть случайная величина и , следовательно, имеет свой закон распределения Py(y 1, a 2, …, ak) Py(y 2, a 1, a 2, …, ak) …………………. . Py(yn, a 1, a 2, …, ak);

Выборка и ее свойства Свойства случайной выборки: 1. Каждый элемент выборки есть случайная величина с тем же законом распределения, что и случайная величина Y 2. Все значения, входящие в выборку независимые величины Тогда для них справедлива теорема умножения вероятностей: Py(y 1, y 2, …, yn. A)=Py(t 1, A) Py(t 2, A)… Py(tn, A) Задача заключается в том, чтобы найти процедуры, с Это выражение – закон распределения выборки помощью которых можно найти значения параметров распределения A = F(y 1, y 2, …, yn)

Метод наименьших квадратов Теорема Гаусса-Маркова Постановка задачи. Имеем уравнение множественной регрессии в виде: (1. 1) где: ai – неизвестные параметры модели xit – регрессоры (экзогенные переменные модели) yt – эндогенная переменная Задача. Подобрать некоторую процедуру (правило) расчета неизвестных параметров модели, которые удовлетворяли хотя бы свойству состоятельности

Схема Гаусса - Маркова Постановка задачи: Имеем случайную выборку наблюдений за поведением экономического объекта объемом n Выборка наблюдений за переменными модели (1. 1) Первый индекс – номер регрессора Второй индекс – номер наблюдения (1. 2) - Система уравнений наблюдений, связывающая наблюдения в выборке

Схема Гаусса - Маркова Найти: 1. Оценки параметров линейной модели множественной регрессии 2. Стандартные ошибки (СКО) оценок параметров 3. Стандартную ошибку случайного возмущения 4. Стандартную ошибку прогноза эндогенной переменной

Схема Гаусса - Маркова Сформируем вектора и матрицу коэффициентов на основе системы (1. 2) Y – вектор выборочных значений эндогенной переменной U – вектор выборочных значений случайного возмущения A - вектор неизвестных параметров модели X – матрица коэффициентов при неизвестных параметрах

Карл Фридрих Гаусс Время жизни 30. 04. 1777 - 23. 02. 1855 Научная сфера – математика, физика, астрономия Андрей Андреевич Марков Время жизни 14. 06. 1856 - 20. 07. 1922 Научная сфера - математика

Теорема Гаусса - Маркова Теорема Если матрица Х неколлинеарна и вектор случайных возмущений удовлетворяет следующим требованиям: Математическое ожидание всех случайных возмущений равно нулю Дисперсия случайных возмущений постоянна во всех наблюдениях (условие ГОМОСКЕДАСТИЧНОСТИ) Случайные возмущения в разных наблюдениях не зависимы Случайные возмущения и регрессоры не зависимы

Теорема Гаусса - Маркова Тогда наилучшей линейной процедурой оценки параметров модели (1. 1) является: (1. 3) которая удовлетворяет методу наименьших квадратов

Теорема Гаусса - Маркова Доказательство: Воспользуемся методом наименьших квадратов (1. 4) где (1. 5) Подставив (1. 5) в (1. 4) получим (1. 6)

Теорема Гаусса - Маркова Для получения необходимого условия экстремума дифференцируем (7. 6) по вектору параметров Откуда система нормальных уравнений для определения искомых параметров получает вид (1. 7) Решение системы (7. 7) в матричном виде есть Выражение (1. 3) доказано

Теорема Гаусса - Маркова Докажем несмещенность оценок (1. 3) Несмещенность оценки (1. 3) доказана Вычислим ковариационную матрицу оценок (1. 3) В результате получено выражение (1. 4)

Уравнение парной регрессии Построить модель типа Y=a 0+a 1 x +u, по данным выборки наблюдений за переменными Y и x объемом n В схеме Гаусса-Маркова имеем: 1. Вычисляем матрицы (XTX) и (XTX)-1

Уравнение парной регрессии 2. Вычисляем XTY Система нормальных уравнений (1. 7) принимает вид:

Уравнение парной регрессии 3. Вычисляем оценку вектора параметров а

Уравнение парной регрессии Вычислим дисперсии (ковариационную матрицу) параметров модели Следовательно: 1. 8 1. 9 1. 10

Уравнение парной регрессии Расчет дисперсии прогнозирования Прогноз осуществляется в точке Z={1, z}Т (1. 11)

Решение задачи в EXCEL В табличном процессоре Excel Существуют как минимум две функции, позволяющих получить оценки параметров линейной модели: - ЛИНЕЙН - РЕГРЕССИЯ Функция ЛИНЕЙН размещена в разделе ФУНКЦИИСТАТИСТИЧЕСКИЕ Функция РЕГРЕССИЯ в разделе АНАЛИЗ ДАННЫХ

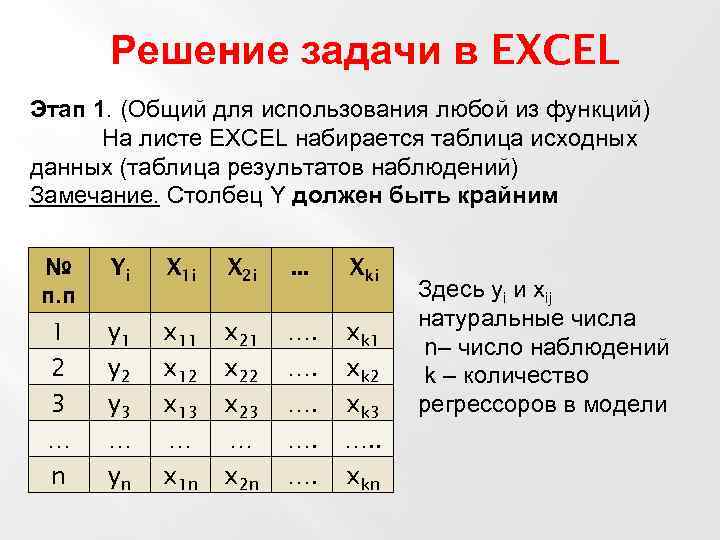Решение задачи в EXCEL Этап 1. (Общий для использования любой из функций) На листе EXCEL набирается таблица исходных данных (таблица результатов наблюдений) Замечание. Столбец Y должен быть крайним № п. п Yi X 1 i X 2 i . . . Xki 1 2 3 … n y 1 y 2 y 3 … yn x 11 x 12 x 13 … x 1 n x 21 x 22 x 23 … x 2 n …. …. …. xk 1 xk 2 xk 3 …. . xkn Здесь yi и xij натуральные числа n– число наблюдений k – количество регрессоров в модели

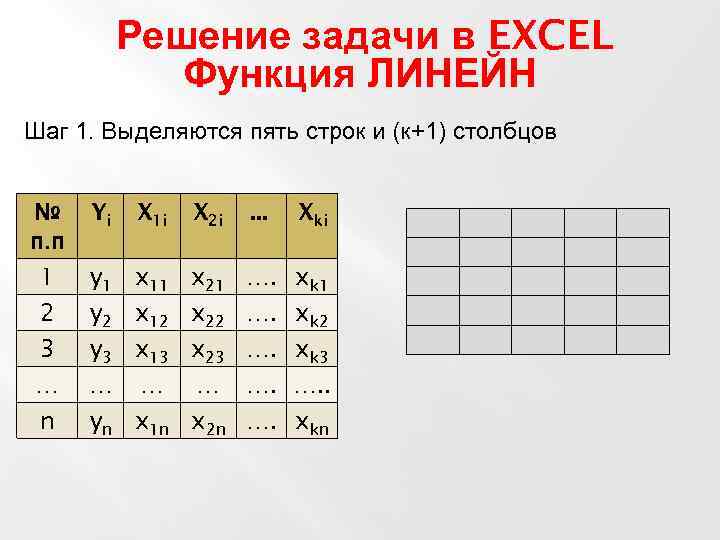Решение задачи в EXCEL Функция ЛИНЕЙН Шаг 1. Выделяются пять строк и (к+1) столбцов № п. п Yi X 1 i X 2 i . . . Xki 1 2 3 … n y 1 y 2 y 3 … yn x 11 x 12 x 13 … x 1 n x 21 x 22 x 23 … x 2 n …. …. …. xk 1 xk 2 xk 3 …. . xkn

Решение задачи в EXCEL Функция ЛИНЕЙН Шаг 2. Вызывается функция ЛИНЕЙН Вместо «ОК» Набирается комбинация Cntr+Shift+Enter

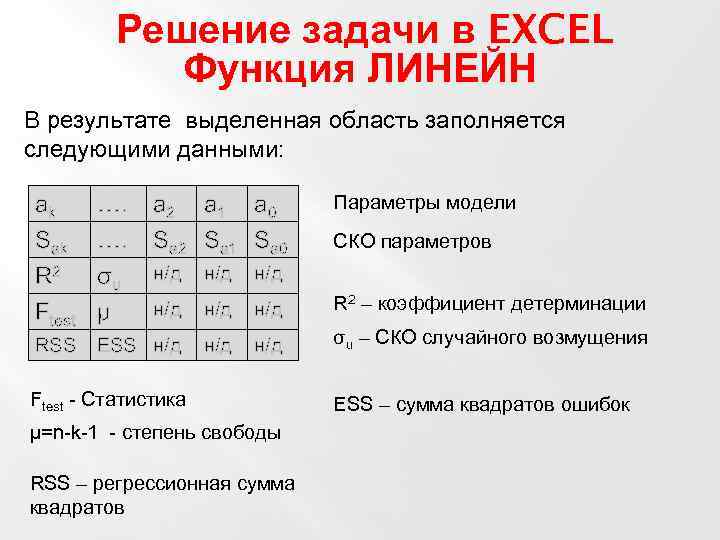Решение задачи в EXCEL Функция ЛИНЕЙН В результате выделенная область заполняется следующими данными: a 2 a 1 a 0 Sa 2 Sa 1 Sa 0 Параметры модели ak Sak R 2 Ftest …. …. σu μ н/д н/д R 2 – коэффициент детерминации RSS ESS н/д н/д σu – СКО случайного возмущения н/д СКО параметров н/д Ftest - Статистика μ=n-k-1 - степень свободы RSS – регрессионная сумма квадратов ESS – сумма квадратов ошибок

Обобщенный метод наименьших квадратов Пусть ковариационная матрица случайных возмущений имеет вид: (1. 8)

Обобщенный метод наименьших квадратов Теорема Эйткена. Если матрица Х коэффициентов уравнения наблюдений имеет полный ранг, М(ui)=0, а матрица ковариаций случайных возмущений имеет вид (11. 9), то наилучшие оценки параметров линейной модели множественной регрессии дает процедура: (1. 9) Если: Ω=E, то (1. 9) превращается в МНК pi≠Const, а Cij=0 – (1. 9) превращается в ВМНК

Взвешенный метод наименьших квадратов Частный случай:

Метод максимального правдоподобия ММП позволяет получить по крайней мере асимптотически несмещенные и эффективные оценки параметров распределения В основе ММП лежит понятие функции правдоподобия выборки Определение. Пусть имеем случайную величину Y, которая имеет функцию плотности вероятностей Py(t, a 1, a 2, …, ak) и случайную выборку Y(y 1, y 2, …, yn )наблюдений за поведением этой величины. Тогда функцией правдоподобия выборки Y(y 1, y 2, …, yn) называется функция L, зависящая от аргументов а={a 1, a 2, …, ak}, и от элементов выборки как от параметров и определяется равенством:

Метод максимального правдоподобия Функция правдоподобия: Основные свойства функции правдоподобия 1. Правая часть равенства имеет смысл значения закона распределения выборки при случайных значениях параметров t 1=y 1, t 2=y 2, …, tn=yn Следовательно, функция правдоподобия L также случайная величина при любых значениях аргументов а={a 1, a 2, …, ak} 2. Все значения функции правдоподобия L ≥ 0 Эти свойства являются следствием свойств выборки

Метод максимального правдоподобия Идея метода В качестве оценки неизвестного параметра принимается такое, которое обеспечивает максимум функции правдоподобия при всех возможных значениях случайной величины Y Математически это выражается так: ãj= argmax(L(a 1, a 2, …, ak, y 1, y 2, …, yn) Очевидно, что оценка ãj зависит от случайной выборки, следовательно, ãj= f(y 1, y 2, …, yn), где f есть процедура вычисления оценки ãj по результатам выборки

Метод максимального правдоподобия Алгоритм решения задачи Предполагается: 1. Вид закона распределения известен; 2. Функция плотности вероятности гладкая во всей области определения Последовательность решения: 1. Составляется функция правдоподобия 2. Вычисляется логарифм функции правдоподобия 3. Оценки параметров получаются в результате решения системы уравнений вида: 4. Проверяется условие максимума функции правдоподобия

Оценка параметров уравнения парной регрессии с помощью ММП Исходные предположения 1. Уравнение имеет вид: yt=a 0 + a 1 xt + ut 2. Случайное возмущение имеет нормальное распределение с параметрами 0 и σu 3. Для получения ММП-оценок имеем выборку из n наблюдений Тогда: Закон распределения для случайного возмущения принимает вид:

Оценка параметров уравнения парной регрессии с помощью ММП 1. Функция правдоподобия получит вид: 2. Логарифм функции правдоподобия

Оценка параметров уравнения парной регрессии с помощью ММП 3. Составляем уравнения для вычисления оценок a 0 и a 1 1. 11 Решение системы (1. 11) совпадает с выражениями (1. 8) и (1. 9), полученными методом наименьших квадратов

Эффективность ММП-оценок Метод проверки условия эффективности базируется на использовании неравенства Рао-Крамера Оно позволяет оценить нижнюю границу точности, с которой можно несмещенно оценить неизвестные параметры Нижняя граница соответствует минимальной дисперсии оценки Следовательно, если дисперсия полученной оценки равна нижней границе, то эта оценка удовлетворяет условию эффективности

Эффективность ММП-оценок Теорема. Для любой ковариационной матрицы любой несмещенной оценки вектора параметров «а» неравенство Рао-Крамера имеет вид: Cov(ã, ã) ≥ I-1 где: I – квадратная матрица, информационная матрица Фишера: Если число оцениваемых параметров равно 1, то матрица Фишера вырождается в число, которое называют информационным количеством Фишера

Эффективность ММП-оценок Замечание. Можно показать, если случайная переменная u имеет нормальный закон распределения, то оценки параметров модели будут несмещенными и эффективными. В противном случае ММП обеспечивает получение состоятельных оценок Замечание. ММП обеспечивает получение состоятельных оценок без каких-либо дополнительных условий В этом его преимущество перед МНК Необходимость знания закона распределения случайной переменной затрудняет его реальное применение

Оценка параметров уравнения парной регрессии с помощью ММП Исходные предположения 1. Уравнение имеет вид: yt=a 0 + a 1 xt + ut 2. Случайное возмущение имеет нормальное распределение с параметрами 0 и σu 3. Для получения ММП-оценок имеем выборку из n наблюдений Тогда: Закон распределения для случайного возмущения принимает вид:

Оценка параметров линей ной модели Выводы: 1. Применяются два основных метода для получения по крайней мере состоятельных оценок параметров линейной модели множественной регрессии: метод максимального правдоподобия и метод наименьших квадратов 2. В общем случае получение состоятельных оценок обеспечивает процедура ОМНК, сформулированная в теореме Эиткена 3. В условия гетероскедастичности случайных возмущений состоятельные оценки дает ВМНК (частный случай ОМНК) 4. При выполнении условий теоремы Гаусса-Маркова МНК обеспечивает состоятельные оценки