ЭКОНОМЕТРИКА Лекция 10 Тестирование модели на гомоскедастичность остатков

ЭКОНОМЕТРИКА Лекция 10 Тестирование модели на гомоскедастичность остатков Взвешенный метод наименьших квадратов 1

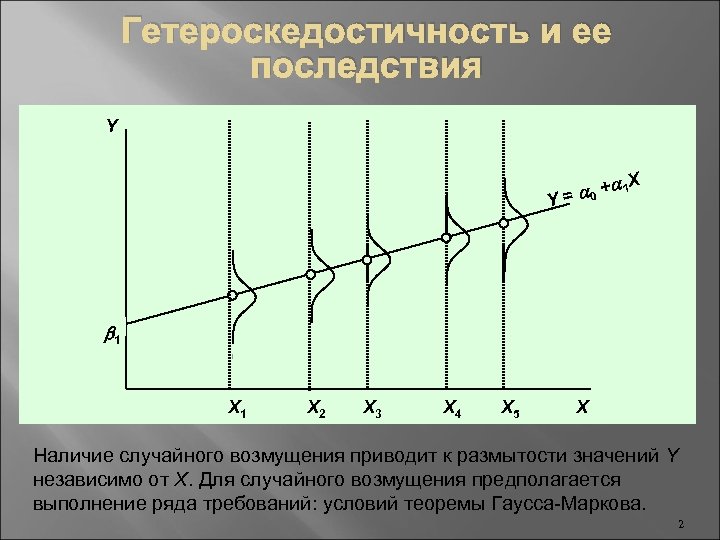Гетероскедостичность и ее последствия Y X +a 1 = a 0 Y b 1 X 2 X 3 X 4 X 5 X Наличие случайного возмущения приводит к размытости значений Y независимо от X. Для случайного возмущения предполагается выполнение ряда требований: условий теоремы Гаусса-Маркова. 2

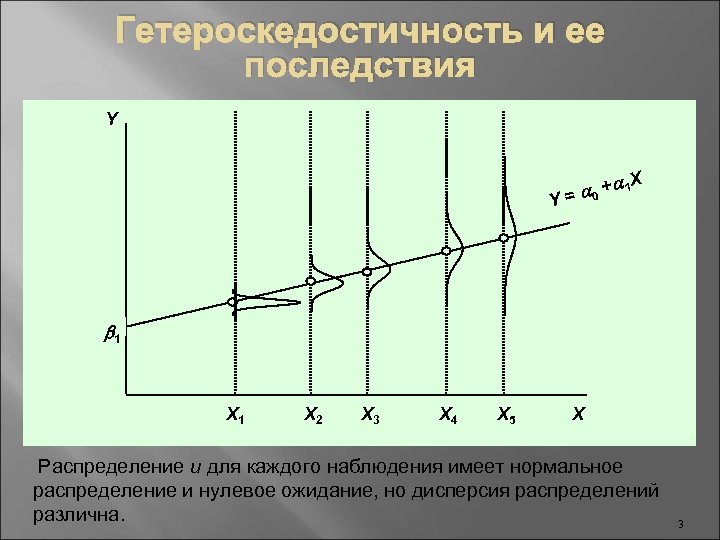Гетероскедостичность и ее последствия Y X +a 1 = a 0 Y b 1 X 2 X 3 X 4 X 5 X Распределение u для каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия распределений различна. 3

Гетероскедостичность и ее последствия Условия обеспечивающие гомоскедастичность (однородность) случайных возмущений: 1. Средние значения случайных возмущений в каждом наблюдении равно нулю 2. Распределения одинаковы для всех наблюдений 4

Гетероскедостичность и ее последствия Последствия нарушения условия гомоскедастичности случайных возмущений: 1. Потеря эффективности оценок коэффициентов регрессии, т. е. можно найти другие, отличные от МНК и более эффективные оценки 2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки 5

Тест Голдфелда-Квандта Данный тест предназначен для того, чтобы проверить гипотезу об отсутствии гетероскедастичности случайных возмущений в схеме Гаусса-Маркова 1. Случай уравнения парной регрессии Имеем спецификацию модели в виде: Yt=a 0 + a 1 xt+ut Имеем выборку в объеме n наблюдений за переменными Yt и xt для оценки параметров этой модели Задача: проверить гипотезу об отсутствии гетероскедастичности в полученной модели 6

Тест Голдфелда-Квандта В основе теста лежат два предположения: 1. Случайные возмущения подчиняются нормальному закону распределения 2. Стандартные ошибки случайных возмущений σ(ut) пропорциональны значениям регрессора xt. 7

Алгоритм применения теста Голдфелда-Квандта Шаг 1. Имеющаяся выборка из n наблюдений сортируется по возрастанию значений регрессора х Шаг 2. Полученная в результате сортировки выборка делится на три примерно равные части Шаг 3. Для первой и третьей частей выборки строятся модели парной регрессии, т. е. для них вычисляются оценки параметров a 0 и a 1 В результате получаются две модели парной регрессии (для каждой части общей выборки): Y 1=ã 01 + ã 11 x +u 1 (10. 1) Y 3=ã 03 + ã 13 x +u 3 (10. 2) Исходя из принятых допущений, считается, что, если ошибки случайных возмущений в «первой» и «третьей» частях выборки будут равны, то условие гомоскедостичности выполняется 8

Алгоритм применения теста Голдфелда-Квандта Шаг 4. Для уравнений (10. 1) и (10. 2) вычисляются значения ESS 1 и ESS 3. Где ESS=Σ(ui 2)=Σ(yi-ã 0 -ã 1 xi)2 Шаг 5. Проверяется гипотеза о равенстве σu 1 и σu 3 5. 1. Формируется случайная переменная GQ в виде: В схеме Гаусса-Маркова переменная GQ имеет закон распределения Фишера. 9

Алгоритм применения теста Голдфелда-Квандта 5. 2. Вычисленное значение GQ сравнивается с критическим значением Fкр(Pдов, n 1, n 3): Если GQ ≤ Fкр(Pдов, n 1, n 3) и 1/GQ ≤ Fкр(Pдов, n 1, n 3), то гипотеза о гомоскедастичности случайных возмущений принимается Случай уравнения множественной регрессии. Yt=a 0+a 1 x 1 t+a 2 x 2 t+a 3 x 3 t+ut Сортировка проводится по величине р=|x 1|+|x 2|+|x 3| Если интерес представляет конкретный регрессор, который приводит к гетероскедастичности, алгоритм повторяется для каждого регрессора в отдельности В результате обнаруживается регрессор вызывающий 10 гетероскедастичность

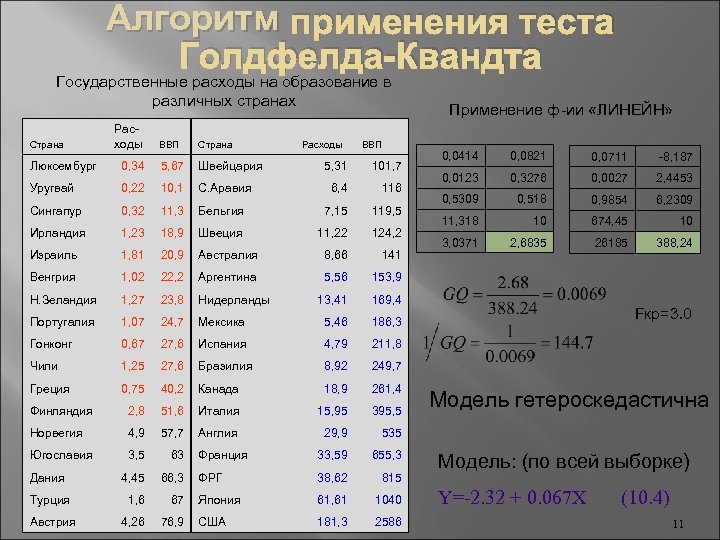Алгоритм применения теста Голдфелда-Квандта Государственные расходы на образование в различных странах Страна Расходы ВВП Страна Люксембург 0, 34 5, 67 Швейцария Уругвай 0, 22 10, 1 С. Аравия Сингапур 0, 32 11, 3 Ирландия 1, 23 Израиль Расходы ВВП 5, 31 101, 7 6, 4 116 Бельгия 7, 15 119, 5 18, 9 Швеция 11, 22 124, 2 1, 81 20, 9 Австралия 8, 66 141 Венгрия 1, 02 22, 2 Аргентина 5, 56 1, 27 23, 8 Нидерланды 13, 41 1, 07 24, 7 Мексика 5, 46 0, 67 27, 6 Испания 4, 79 1, 25 27, 6 Бразилия 8, 92 0, 75 40, 2 Канада 18, 9 261, 4 Финляндия 2, 8 51, 6 Италия 15, 95 395, 5 Норвегия 4, 9 57, 7 Англия 29, 9 3, 5 63 Франция 33, 59 655, 3 Дания 4, 45 66, 3 ФРГ 38, 62 815 Турция 1, 6 67 Япония 61, 61 1040 Австрия 4, 26 76, 9 США 181, 3 2586 0, 3276 0, 0027 2, 4453 0, 5309 0, 518 0, 9854 6, 2309 11, 318 10 674, 45 10 3, 0371 2, 6835 26185 388, 24 535 Югославия 0, 0123 249, 7 Греция -8, 187 211, 8 Чили 0, 0711 186, 3 Гонконг 0, 0821 169, 4 Португалия 0, 0414 153, 9 Н. Зеландия Применение ф-ии «ЛИНЕЙН» Fкр=3. 0 Модель гетероскедастична Модель: (по всей выборке) Y=-2. 32 + 0. 067 X (10. 4) 11

Алгоритм применения теста Голдфелда-Квандта Случай уравнения множественной регрессии Имеем: 1. Спецификацию модели: Yt=a 0+a 1 x 1 t+a 2 x 2 t+a 3 x 3 t+ut (10. 5) 2. Выборку наблюдений за переменными {Y, x 1, x 2, x 3} 3. Модель по этим данным гетероскедастична 4. Известны значения σ(ut) в каждом наблюдении Задача: преобразовать модель так, чтобы случайные возмущения были гомоскедастичны 12

Метод исправления гетероскедастичности Способ 1. Делится каждое уравнение наблюдений на свое σ(ut) и получается: (10. 6) Тогда дисперсия случайного возмущения в каждом уравнении наблюдений есть: Модель (10. 6) в каждом уравнении наблюдения имеет одинаковые дисперсии случайного возмущения равные 1 Недостаток способа – оценить σ(ut) не возможно! 13

Метод исправления гетероскедастичности Способ 2. Предполагаем, что σ(ut)=λxkt, где xkt регрессор «вызывающий» гетероскедастичность Пусть для примера это регрессор x 2 t Уравнение (10. 5) делится на значение этого регрессора. (10. 7) Дисперсия случайного возмущения при этом есть: Уравнения модели (10. 7) имеют постоянную дисперсию случайного возмущения равную λ 2

Метод исправления гетероскедастичности Если регрессоров, приводящих к гетероскедастичности, несколько, то делается предположение: Обе части модели (10. 5) делятся на величину Σ│xj│ Тогда дисперсия случайного возмущения полученной модели есть: 15

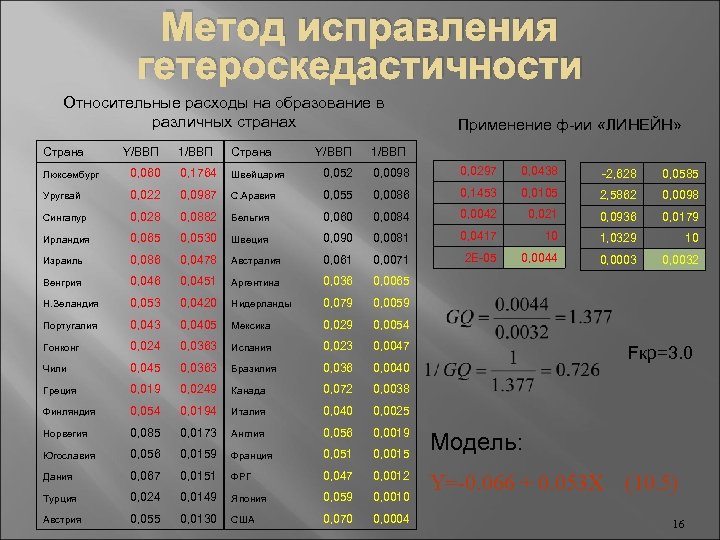Метод исправления гетероскедастичности Относительные расходы на образование в различных странах Страна Y/ВВП 1/ВВП Страна Y/ВВП Применение ф-ии «ЛИНЕЙН» 1/ВВП Люксембург 0, 060 0, 1764 Швейцария 0, 052 0, 0098 0, 0297 0, 0438 -2, 628 0, 0585 Уругвай 0, 022 0, 0987 С. Аравия 0, 055 0, 0086 0, 1453 0, 0105 2, 5862 0, 0098 Сингапур 0, 028 0, 0882 Бельгия 0, 060 0, 0084 0, 0042 0, 021 0, 0936 0, 0179 Ирландия 0, 065 0, 0530 Швеция 0, 090 0, 0081 0, 0417 10 1, 0329 10 Израиль 0, 086 0, 0478 Австралия 0, 061 0, 0071 2 E-05 0, 0044 0, 0003 0, 0032 Венгрия 0, 046 0, 0451 Аргентина 0, 036 0, 0065 Н. Зеландия 0, 053 0, 0420 Нидерланды 0, 079 0, 0059 Португалия 0, 043 0, 0405 Мексика 0, 029 0, 0054 Гонконг 0, 024 0, 0363 Испания 0, 023 0, 0047 Чили 0, 045 0, 0363 Бразилия 0, 036 0, 0040 Греция 0, 019 0, 0249 Канада 0, 072 0, 0038 Финляндия 0, 054 0, 0194 Италия 0, 040 0, 0025 Норвегия 0, 085 0, 0173 Англия 0, 056 0, 0019 Югославия 0, 056 0, 0159 Франция 0, 051 0, 0015 Дания 0, 067 0, 0151 ФРГ 0, 047 0, 0012 Турция 0, 024 0, 0149 Япония 0, 059 0, 0010 Австрия 0, 055 0, 0130 США 0, 070 0, 0004 Fкр=3. 0 Модель: Y=-0. 066 + 0. 053 X (10. 5) 16

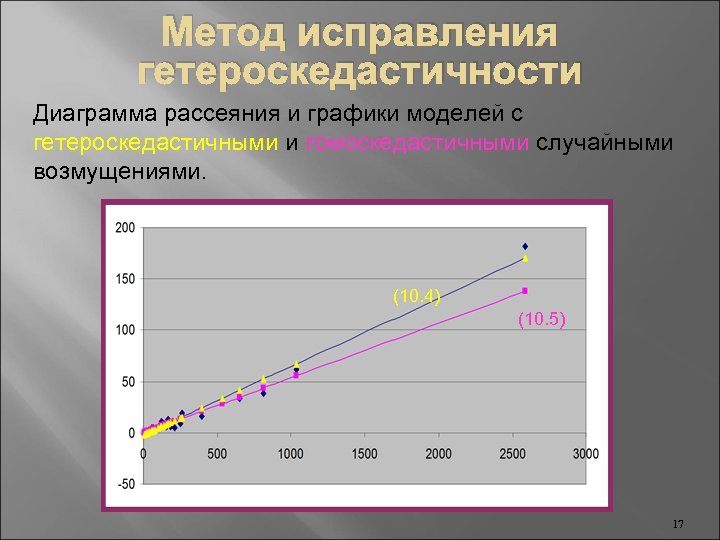Метод исправления гетероскедастичности Диаграмма рассеяния и графики моделей с гетероскедастичными и гомоскедастичными случайными возмущениями. (10. 4) (10. 5) 17

Метод исправления гетероскедастичности 2. Случай уравнения множественной регрессии Продолжим рассмотрение предыдущего примера, но в качестве дополнительного регрессора примем х2 – численность населения Здесь: Y – расходы на образование x 1 - размер ВВП x 2 - численность населения 18

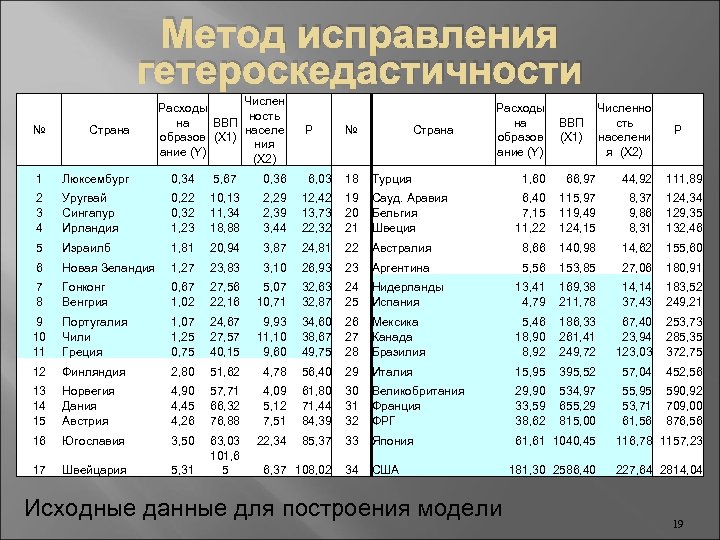Метод исправления гетероскедастичности Числен Расходы ность на ВВП населе образов (X 1) ния ание (Y) (X 2) № Страна Р № 1 Люксембург 0, 34 5, 67 2 3 4 Уругвай Сингапур Ирландия 0, 22 0, 32 1, 23 5 Израилб 6 Страна 0, 36 6, 03 18 Турция 10, 13 11, 34 18, 88 2, 29 2, 39 3, 44 12, 42 13, 73 22, 32 19 20 21 Сауд. Аравия Бельгия Швеция 1, 81 20, 94 3, 87 24, 81 22 Новая Зеландия 1, 27 23, 83 3, 10 26, 93 7 8 Гонконг Венгрия 0, 67 1, 02 27, 56 22, 16 5, 07 10, 71 9 10 11 Португалия Чили Греция 1, 07 1, 25 0, 75 24, 67 27, 57 40, 15 12 Финляндия 2, 80 13 14 15 Норвегия Дания Австрия 16 17 Расходы на образов ание (Y) ВВП (X 1) Численно сть населени я (X 2) Р 1, 60 66, 97 44, 92 111, 89 6, 40 7, 15 11, 22 115, 97 119, 49 124, 15 8, 37 9, 86 8, 31 124, 34 129, 35 132, 46 Австралия 8, 66 140, 98 14, 62 155, 60 23 Аргентина 5, 56 153, 85 27, 06 180, 91 32, 63 32, 87 24 25 Нидерланды Испания 13, 41 4, 79 169, 38 211, 78 14, 14 37, 43 183, 52 249, 21 9, 93 11, 10 9, 60 34, 60 38, 67 49, 75 26 27 28 Мексика Канада Бразилия 5, 46 18, 90 8, 92 186, 33 261, 41 249, 72 67, 40 23, 94 123, 03 253, 73 285, 35 372, 75 51, 62 4, 78 56, 40 29 Италия 15, 95 395, 52 57, 04 452, 56 4, 90 4, 45 4, 26 57, 71 66, 32 76, 88 4, 09 5, 12 7, 51 61, 80 71, 44 84, 39 30 31 32 Великобритания Франция ФРГ 29, 90 33, 59 38, 62 534, 97 655, 29 815, 00 55, 95 53, 71 61, 56 590, 92 709, 00 876, 56 Югославия 3, 50 22, 34 85, 37 33 Япония 61, 61 1040, 45 116, 78 1157, 23 Швейцария 5, 31 63, 03 101, 6 5 6, 37 108, 02 34 США 181, 30 2586, 40 227, 64 2814, 04 Исходные данные для построения модели 19

Взвешенный метод наименьших квадратов Предполагается, что дисперсию случайного возмущения можно представить в виде: где: σ02 – дисперсия единицы веса λ – заданная константа, например ± 0. 5; ± 1; ± 2; Вес случайного остатка вычисляется по правилу: 20

Взвешенный метод наименьших квадратов Рассмотренные способы устранения гетероскедастичности носят название «Взвешенный метод наименьших квадратов» . Теорема. Если в схеме Гаусса-Маркова не выполняется предпосылка о гомоскедастичности случайных возмущений, то наилучшей линейной процедурой оценки параметров модели является: где: Р матрица ковариаций случайных возмущений в уравнения наблюдений: 21

Проблема гетероскедастичности Выводы: 1. Гетероскедастичность приводит к смещенности оценок параметров модели 2. Одним из способов обнаружения гетероскедастичности является тест Голдфелда-Квандта 3. Взвешенный метод наименьших квадратов позволяет получить несмещенные оценки параметров модели в условиях гетероскедастичности 22