ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ Эконометрика наука изучающая конкретные количественные

ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ Эконометрика – наука, изучающая конкретные количественные взаимосвязи экономических объектов и процессов с помощью математических и статистических методов и моделей. Переменные, участвующие в любой эконометрической модели: результирующая (зависимая, эндогенная или результативный признак) переменная У - характеризует результат или эффективность функционирования экономической системы. Результирующая переменная всегда случайна (стохастична); объясняющие (независимые, экзогенные или факторные признаки) переменные X - поддаются регистрации и описывают условия функционирования реальной системы. Это аргументы результирующей функции У, могут быть как случайными, так и неслучайными.

Модели временных рядов представляют собой модели зависимости результативного признака от времени • • • Временной ряд экономического показателя имеет тренд, т. е. преобладающую тенденцию. Основная цель создания трендовых моделей экономической динамики – сделать прогноз о развитии изучаемого процесса на предстоящий промежуток времени. Чтобы правильно подобрать наилучший тренд, необходимо знать особенности каждого вида кривых. Наиболее часто в экономике используются полиномиальные, экспоненциальные и S-образные кривые. Простейшие полиномиальные кривые имеют вид: у=а 0+а 1 t (полином первой степени) у=а 0+а 1 t+а 2 t 2 (полином второй степени) у=а 0+а 1 t+а 2 t 2 +а 3 t 3 (полином третьей степени) Параметр а 1 называется линейным приростом, параметр а 2 – ускорением роста, параметр а 3 – изменением ускорения роста. Полиномиальные кривые роста можно использовать для аппроксимации (приближения) и прогнозирования экономических процессов, в которых последующее развитие не зависит от достигнутого уровня .

Корреляция, вычисление коэффициента парной корреляции • Рассматривая зависимости между признаками, необходимо выделить два типа связей. • Первый тип связей – функциональные, которые характеризуются полным соответствием между изменением факторного признака и изменением результативной величины. Этот тип связей выражается в виде формульной зависимости. • Второй тип связей - корреляционные, которые проявляются тогда, когда между изменением двух признаков нет полного соответствия, воздействие отдельных факторов возможно лишь в среднем, при массовом наблюдении фактических данных.

Основная задача корреляционного анализа заключается в выявлении взаимосвязи между случайными переменными путем точечной и интервальной оценки парных (частных) коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации. • С помощью корреляционного анализа решаются следующие задачи: • отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения тесноты связи между ними; • обнаружение ранее неизвестных причинных связей.

Для двух переменных X и Y коэффициент парной корреляции определяется следующим образом: • r y, x= = = Коэффициент корреляции r y, x - число, не имеющее размерности, и принимает значения от -1 до +1.

• где Sx 2, Sy 2 - оценки дисперсий величин X и У. Эти оценки характеризуют степень разброса значений х1, х2, . . . , хn (y 1, y 2, . . . , уn) вокруг своего среднего или вариабельность (изменчивость) этих переменных на множестве наблюдений. • Дисперсия (оценка дисперсии) определяется по формуле: • Sx 2= • В общем случае для получения несмещенной оценки дисперсии сумму квадратов следует делить на число степеней свободы оценки (n-p), где n - объем выборки, р - число наложенных на выборку связей. среднеквадратическое отклонения (стандартное отклонение) или стандартной ошибки переменной X (переменной У) по формуле: • Sx=

• Для качественной оценки коэффициента корреляции применяются шкала Чеддока. Связь может иметь одну из оценок: 0, 1— 0, 3 - слабая; 0, 3— 0, 5 - заметная; 0, 5— 0, 7 - умеренная; 0, 7— 0, 9 - высокая; 0, 9— 1, 0 - весьма высокая. • Оценка значимости коэффициента корреляции при малых объемах выборки, дающая возможность распространить выводы по результатам выборки на генеральную совокупность, выполняется с использованием t-критерия Стьюдента. Фактическое (наблюдаемое) значение этого критерия определяется по формуле t набл =

• Вычисленное по формуле значение t набл сравнивается с критическим значением t-критерия, которое берется из таблицы значений t-критерия Стьюдента с учетом заданного уровня значимости α и числа степеней свободы (n-2). • Если t набл>tтабл, то полученное значение коэффициента корреляции признается значимым (т. е. нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). И между исследуемыми переменными есть тесная статистическая взаимосвязь. • Если значение ry, x близко к нулю, связь между переменными слабая. • Если корреляция между случайными величинами: положительная, то при возрастании одной случайной величины другая имеет тенденцию в среднем возрастать; отрицательная, то при возрастании одной случайной величины другая имеет тенденцию в среднем убывать.

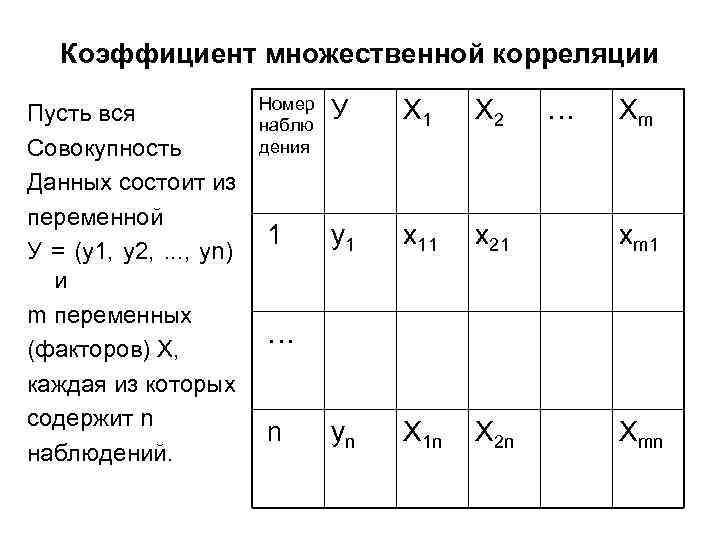Коэффициент множественной корреляции Номер У Пусть вся наблю дения Совокупность Данных состоит из переменной 1 y 1 У = (y 1, y 2, . . . , уn) и m переменных … (факторов) X, каждая из которых содержит n n yn наблюдений. Х 1 Х 2 … Хm x 11 x 21 xm 1 X 1 n X 2 n Xmn

Матрица коэффициентов парной корреляции R симметрична относительно главной диагонали: • • R=

В многомерном корреляционном анализе рассматривается две задачи: , • Определение тесноты связи одной случайной величины с совокупностью остальных величин, включенных в анализ. • Определение тесноты связи между двумя величинами при фиксировании или исключении влияния остальных величин. • Эти задачи решаются соответственно с помощью коэффициентов множественной и частной корреляции.

• Решение первой задачи (определение тесноты связи одной случайной величины с совокупностью остальных величин, включенных в анализ) осуществляется с помощью выборочного коэффициента множественной корреляции по формуле • R j, 1, 2, …, j-1, j+1, …, m= определитель корреляционной матрицы R; Rjj -алгебраическое дополнение элемента rjj матрицы R.

Квадрат коэффициента множественной корреляции R 2 j, 1, 2, …, j-1, j+1, …, m называется выборочным множественным коэффициентом детерминации; он показывает, какую долю вариации (случайного разброса) исследуемой величины Xj. объясняет вариация остальных случайных величин X 1, Х 2, …, Хm. Коэффициенты множественной корреляции и детерминации являются величинами положительными, принимающими значения в интервале от 0 до 1. При приближении коэффициента R 2 к единице можно сделать вывод о тесноте взаимосвязи случайных величин, но не о ее направлении.

• Проверка значимости коэффициента детерминации осуществляется путем сравнения расчетного значения F-критерия Фишера: • Fрасч = • с табличным Fтабл. Табличное значение определяется заданным уровнем значимости α и степенями свободы ν 1=p-1 и ν 2= n-p (где p – количество параметров модели). Коэффициент R 2 значимо отличается от нуля, если выполняется неравенство • Fрасч >Fтабл

• Решение второй задачи (определение тесноты связи между двумя величинами при фиксировании или исключении влияния остальных величин) осуществляется с помощью исследования частной корреляции между величинами при исключении влияния других случайных величин (одной или нескольких). • Выборочный частный коэффициент корреляции определяется по формуле • r j k(1, 2, …, m)= • где Rjk, Rjj, Rkk - алгебраические дополнения к соответствующим элементам матрицы R. Частный коэффициент корреляции, изменяется от -1 до +1.

Линейная модель парной регрессии. • Связь между переменной У и k независимыми факторами X можно охарактеризовать функцией регрессии У= f(Х 1, Х 2, . . . , Хк), которая показывает, каково будет в среднем значение переменной У, если переменные Хi примут конкретные значения. • Линейная связь между переменной У и независимым фактором Х может быть представлена функцией линейной регрессии: у=α+βх

• Для оценки параметров регрессионного уравнения используют метод наименьших квадратов. • Оценки α, β находят путем минимизации суммы квадратов Q(α, β)= Искомые значения α, β удовлетворяют соотношениям:

При анализе качества модели регрессии используется • Коэффициент детерминации • R 2= • εi=yi- • Данный коэффициент показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов, Чем ближе R 2 к единице, тем выше качество модели.

• Коэффициент множественной корреляции (индекс корреляции): • R= • Данный коэффициент универсален, так как он отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных. • Для парной модели регрессии индекс корреляции равен коэффициенту парной корреляции.

• Для оценки качества регрессионных моделей используется также средняя относительная ошибка аппроксимации: • Еотн= Чем меньше рассеяние эмпирических точек вокруг теоретической линии регрессии, тем меньше средняя ошибка аппроксимации; Еотн<7% свидетельствует о хорошем качестве модели.

• Оценка значимости уравнения регрессии позволяет узнать, пригодно уравнение регрессии для практического использования Для проверки значимости модели регрессии используется Fкритерий Фишера, Если расчетное значение, c ν 1=k и ν 2= n-k-1 степенями свободы (k - количество факторов, включенных в модель), больше табличного при заданном уровне значимости α, то модель считается значимой. • Для модели парной регрессии: • Fрасч= • Если Fрасч> Fтабл, то модель значима

В качестве меры точности применяют несмещенную оценку дисперсии остаточной компоненты S 2 Стандартная ошибка Se – корень квадратный из S 2 и вычисляется по формуле: Se= • где k – количество факторов, включенных в модель. • Для модели парной регрессии Se=

• Для анализа статистической значимости параметров модели парной регрессии вычисляют стандартные ошибки коэффициентов • S α= • Sβ=

• Проверка значимости отдельных коэффициентов регрессии связана с определением расчетных значений tкритерия (t-статистики Стьюдента) для соответствующих коэффициентов регрессии: • t α расч= t β расч= . • Расчетные значения t расч сравниваются с табличными t табл. Табличное значение критерия определяется при (n-2) степенях свободы (n – число наблюдений) и соответствующем уровне значимости α. • Если t расч с (n-k-1) степенями свободы больше t табл при заданном уровне значимости , то коэффициент регрессии считается значимым. В противном случае фактор, соответствующий этому коэффициенту, должен быть исключен из модели, а оставшиеся в модели параметры пересчитаны.

• Прогнозированное значение переменной У получается при подстановке в уравнение регрессии ожидаемой величины фактора Х: у= α+βхпрогн. Такой прогноз называется точечным. • у с вероятностью (1 -α) попадут в доверительный интервал: • уЄ[

Полиномиальные модели • Квадратичная модель парной регрессии • у=а 0+а 1 х+а 2 х2 Длянахождения неизвестных коэффициентов а 0, а 1, а 2 используется МНК , который преобразуется в систему уравнений

Оценка качества модели • Коэффициент детерминации R 2 • Коэффициент множественной корреляции (индекс корреляции) R • Стандартная ошибка Se – корень квадратный из S 2 • Анализ статистической значимости параметров модели парной регрессии используют стандартные ошибки коэффициентов S а 1 , S а 2

Оценка тесноты нелинейной связи • При отклонении парной статистической зависимости от линейной коэффициент корреляции теряет свой смысл как характеристика тесноты связи. В этом случае можно воспользоваться таким измерителем связи, как индекс корреляции (корреляционное отношение). • Для определения эмпирического корреляционного отношения совокупность значений результативного признака У разбивают на отдельные группы. В основу группировки кладется исследуемый фактор X.

Методика вычисления корреляционного отношения. . • Группирование данных произведено по оси x, при этом k – число интервалов группирования; mj (j= ) количество элементов выборки в j-ом интервале группирования; n – объем совокупности (n= ) - общее среднее. • Вычисляем среднее значение У в j–й группе: • Вычисляем общую среднюю У:

• Вычисляем межгрупповую дисперсию и общую дисперсию: S yj 2= S y 2= • Корреляционное отношение ή зависимой переменной У по независимой переменной Х : • ή=

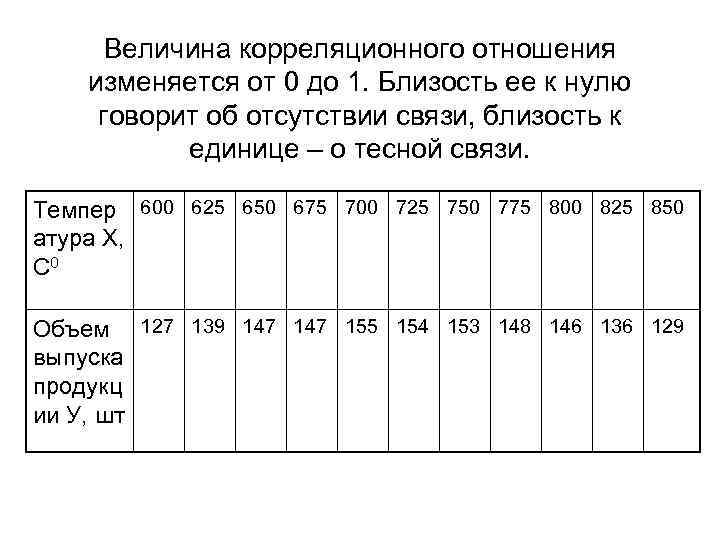Величина корреляционного отношения изменяется от 0 до 1. Близость ее к нулю говорит об отсутствии связи, близость к единице – о тесной связи. Темпер 600 625 650 675 700 725 750 775 800 825 850 атура Х, С 0 Объем 127 139 147 155 154 153 148 146 136 129 выпуска продукц ии У, шт

Пример. • Оценить тесноту связи между объемом выпуска продукции и температурой определенного технологического процесса. Данные, полученные в результате эксперимента, представлены в Таблице. Решение. Значение результативного признака У разобьем на пять групп, т. е. k=5. В основе группировки – исследуемый фактор Х. Вычисления в таблице

Общая средняя: =1/11(2*133+2*147+3*154+2*147+1*132, 5)=143, 727. Межгрупповая дисперсия: S yj 2= =841, 6816/ 11=76, 5165 Общая дисперсия: S y 2 = =942, 18/11=85, 6529. Корреляционное отношение: ή= = 0, 945. Значение ή=0, 945 свидетельствует о наличии сильного нелинейного влияния температуры на объем выпуска продукции. Номер Кол-во Значения yi Среднее значение У ( - )2 группы элементов в j–й группе mj попавшие в j-ю группу в j–й группе 1 2 127; 139 133 17689 2 2 147; 147 21609 3 3 155; 154; 153 154 23716 4 2 148; 146 147 21609 5 2 136; 139 132, 5 17556, 25