EKOHOMI 4 HA KI 6 EPHETUKA
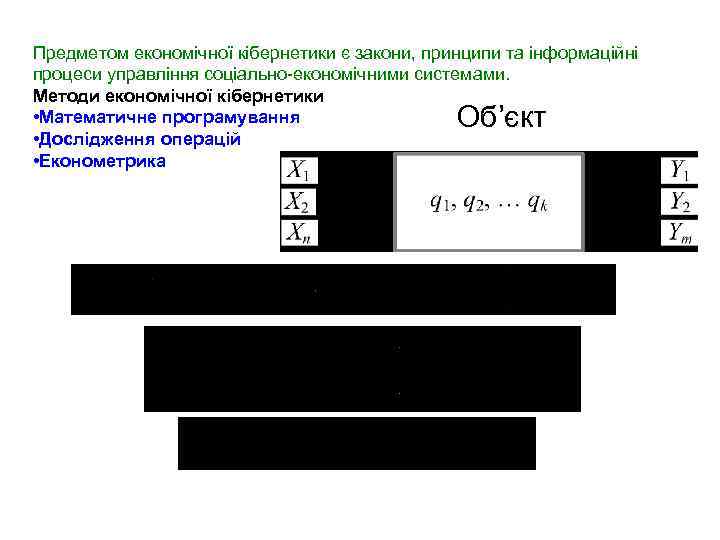Предметом економічної кібернетики є закони, принципи та інформаційні процеси управління соціально-економічними системами. Методи економічної кібернетики • Математичне програмування • Дослідження операцій • Економетрика Об’єкт
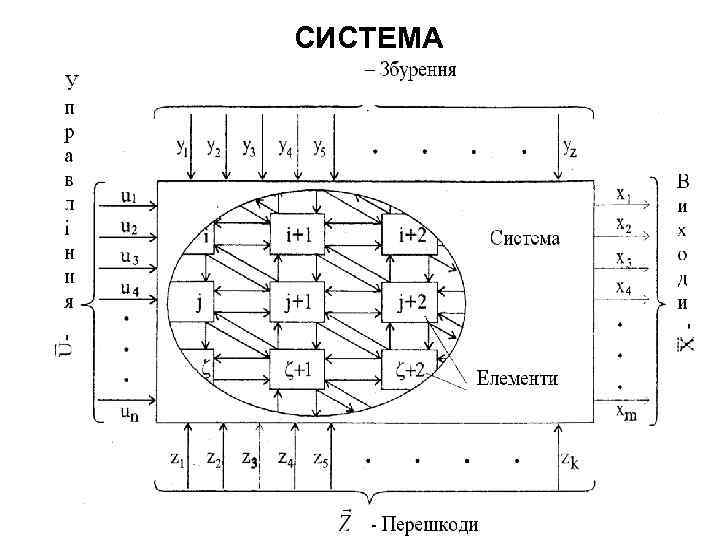СИСТЕМА
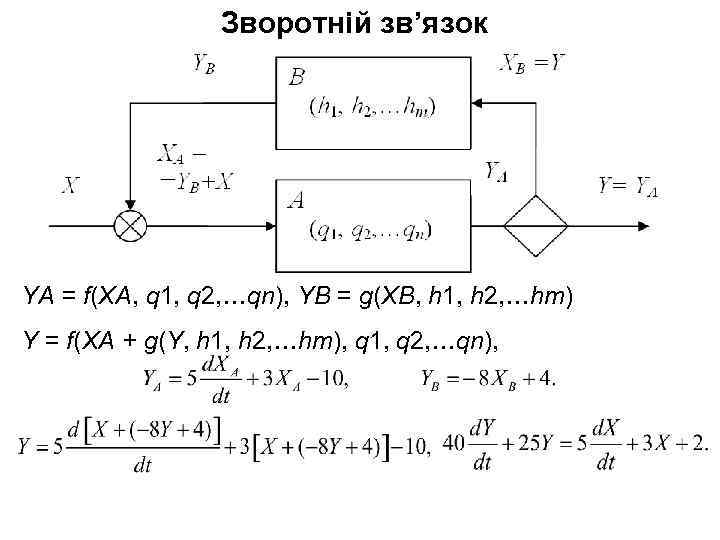Зворотній зв’язок YА = f(XА, q 1, q 2, …qn), YВ = g(XВ, h 1, h 2, …hm) Y = f(XА + g(Y, h 1, h 2, …hm), q 1, q 2, …qn),
ВИКОРИСТАННЯ КОМП'ЮТЕРА (ПАКЕТ MAXIMA) ДЛЯ РОЗВ’ЯЗУВАННЯ ДИФЕРЕНЦІАЛЬНИХ РІВНЯНЬ Синтаксис: Приклад : Розв'язати задачу Коші для диференціального рівняння першого порядку . Початкова умова: Для початкової умови призначений оператор ic 1.
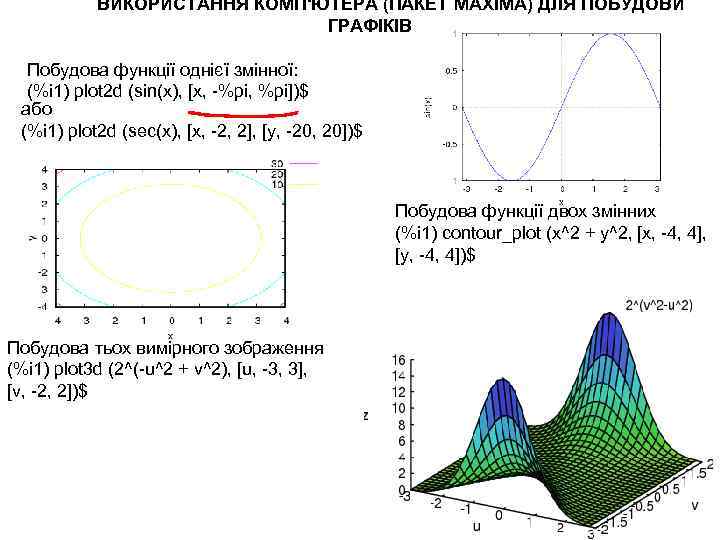ВИКОРИСТАННЯ КОМП'ЮТЕРА (ПАКЕТ MAXIMA) ДЛЯ ПОБУДОВИ ГРАФІКІВ Побудова функції однієї змінної: (%i 1) plot 2 d (sin(x), [x, -%pi, %pi])$ або (%i 1) plot 2 d (sec(x), [x, -2, 2], [y, -20, 20])$ Побудова функції двох змінних (%i 1) contour_plot (x^2 + y^2, [x, -4, 4], [y, -4, 4])$ Побудова тьох вимірного зображення (%i 1) plot 3 d (2^(-u^2 + v^2), [u, -3, 3], [v, -2, 2])$
Інформація ОСНОВНІ ЗАКОНИ ТА ПРИНЦИПИ КІБЕРНЕТИКИ • Закон необхідної різноманітності. • Принцип вибору рішень на підставі відбору і перетворення інформації • Принцип обов'язковості зворотного зв'язку • Принцип зовнішнього доповнення
Основний порядок побудови системи управління об’єктами та системами 1. 2. 3. 4. 5. 6. 7. 8. Визначити межі об‘єкту та його тип (об‘єкт чи система). У випадку визначення системи, розбити її на об‘єкти і визначити структуру зв’язків поміж ними. Визначити перелік вхідних та вихідних факторів Розкласифікувати вхідні фактори на 3 типи. Зібрати числові дані про діяльність об’єкту чи системи за якомога більший період і розташувати їх у вигляді таблиці , в якій праворуч стоять колонки зі вхідними, а ліворуч – колонки з вихідними факторами. Провести статистичний аналіз даних з визначенням їх достовірності та достатності. Якщо перевірка показала недостатність, провести додаткове спостереження і доповнити таблицю. Визначитися з типом моделі, яка описуватиме дії об‘єкту чи системи Розрахувати числові коефіцієнти моделі та визначити її адекватність та прогнозуючі властивості. Розрахувати такі значення для факторів управління, які б дозволили отримати найкращі значення вихідних факторів.
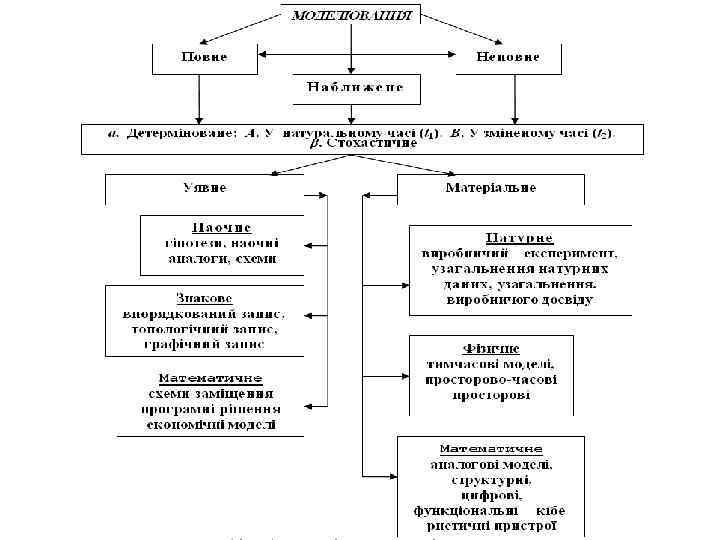
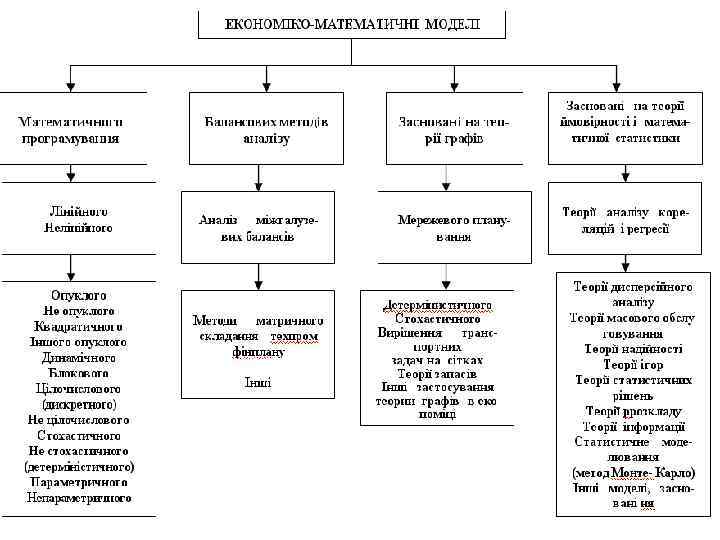
Приклади кібернетичних моделей соціально-економічних систем Модель нарахування відсотків Моделі фінансових розрахунків Модел Кобба-Дугласа z=b 0 xb 1 yb 2 Динамічні моделі Пістунова-Чухлєбової схильності до банкрутства торгово-транспортних підприємств Дніпропетровської області
АНАЛІЗ Статистичний
Дисперсійний аналіз Аналіз експертних висновків За Спірменом За Кендалом
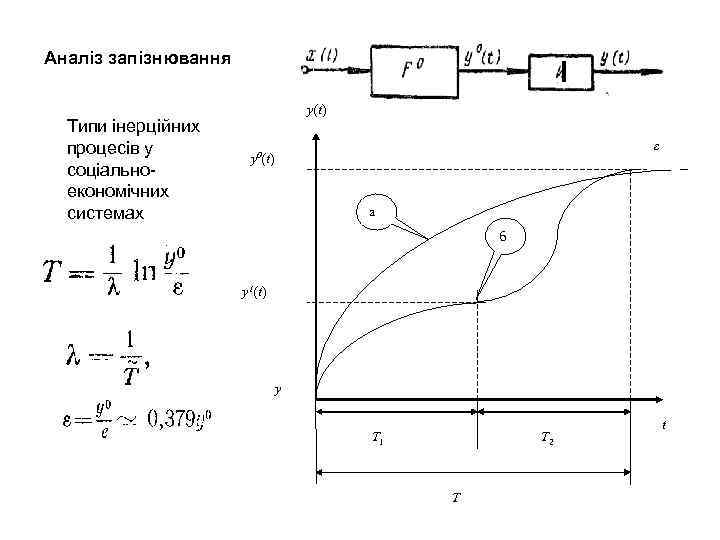Аналіз запізнювання Типи інерційних процесів у соціальноекономічних системах І y(t) ε y 0(t) а б y 1(t) y T 1 T 2 T t
Спектральний аналіз Ряд Фур'є — в математиці — спосіб представлення довільної складної функції сумою простіших. В загальному випадку кількість таких функцій може бути нескінченною, при цьому чим більше таких функцій враховується при розрахунку, тим вищою стає кінцева точність представлення даної функції. В більшості випадків в якості найпростіших використовуються тригонометричні функції синуса і косинуса. В цьому випадку ряд Фур'є називаеться тригонометричним, а обчислення такого ряду часто називаютьрозкладом на гармоніки.
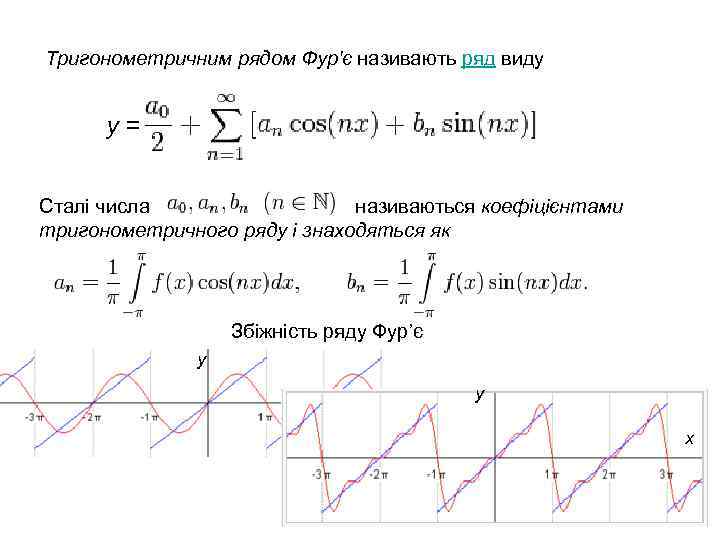Тригонометричним рядом Фур'є називають ряд виду y = Сталі числа називаються коефіцієнтами тригонометричного ряду і знаходяться як Збіжність ряду Фур’є y y x
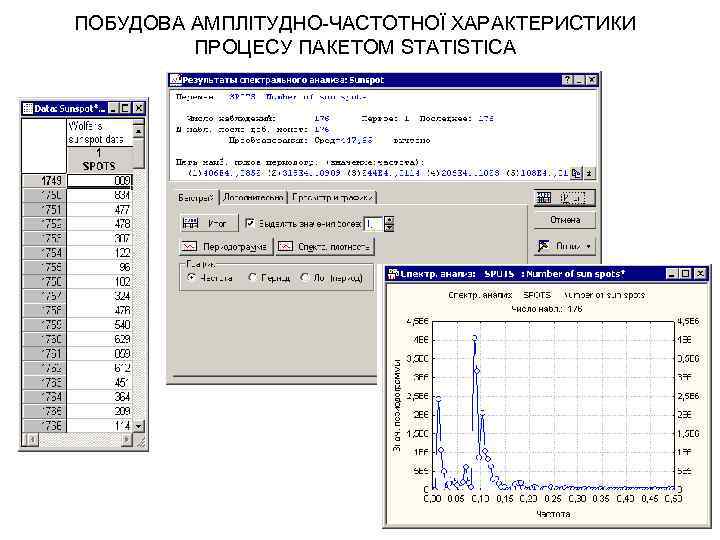ПОБУДОВА АМПЛІТУДНО-ЧАСТОТНОЇ ХАРАКТЕРИСТИКИ ПРОЦЕСУ ПАКЕТОМ STATISTICA
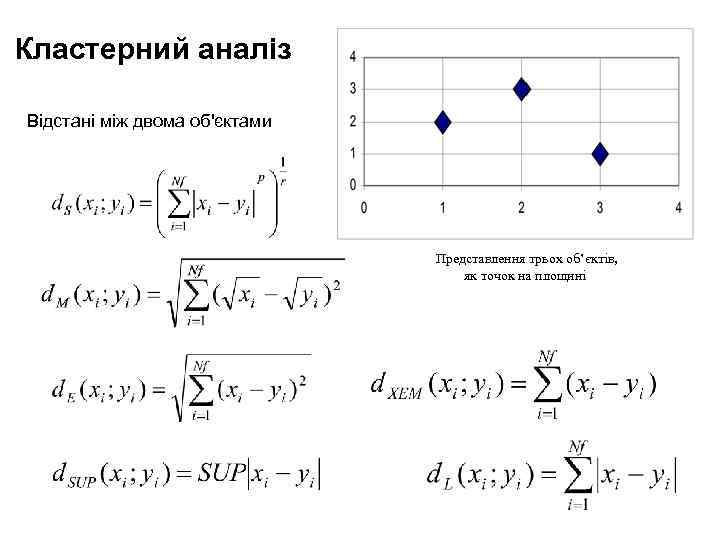Кластерний аналіз Відстані між двома об'єктами Представлення трьох об’єктів, як точок на площині
Кластеризація повним перебором об'єктів Об'єкти 1 2 3 4 5 1 0 0 0 1 2 1 0 0 1 3 0 0 0 1 1 2 4 0 0 1 5 0 0 0 Сума по стов пцям 1 1 1 5 1 2 3 4 1 0 2 0, 89 3 0, 41 0, 86 4 0, 74 0, 87 0, 96 5 0, 46 0, 61 0, 66 0, 62 5 0, 89 0, 41 0, 74 0, 46 0 0, 86 0, 87 0, 61 0 0, 96 0, 66 0 0, 62 0 Сума по клас тера м Кла с т е р и
Синтез статистичних лінійних та квазілінійних моделей Можливі перетворення х1 х2, х1/ х2, х1 -х2, log х1 х2, Приклад нормування-денормування у = а 0 + а 1 x + а 2 x 2 Lnу = а 0 + а 1*Lnx 1 + а 2*Lnx 2
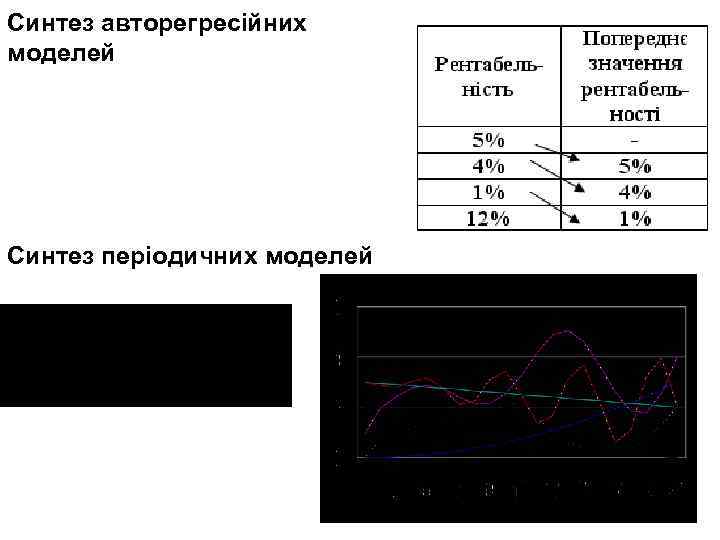Синтез авторегресійних моделей Синтез періодичних моделей
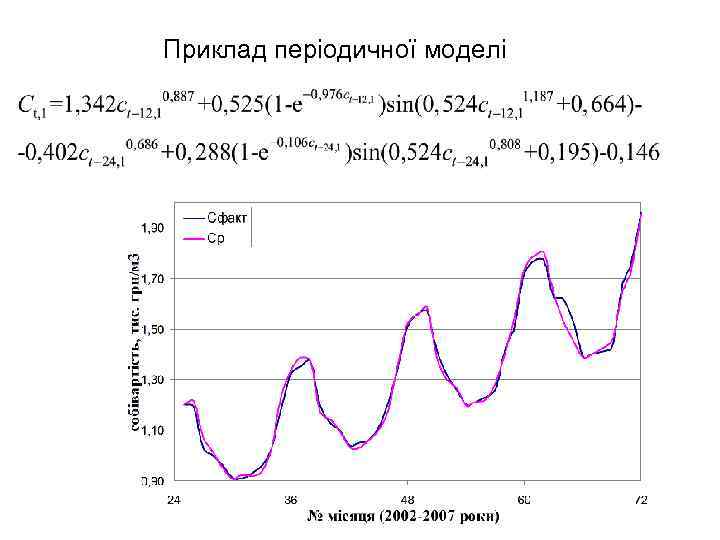Приклад періодичної моделі
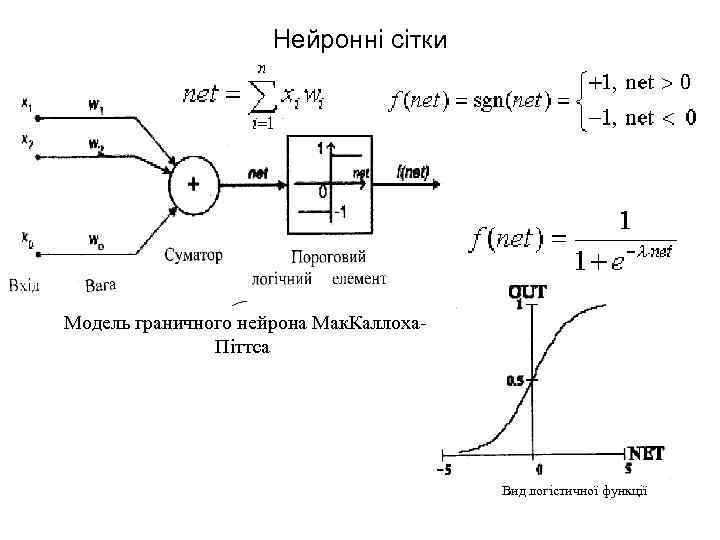Нейронні сітки Модель граничного нейрона Мак. Каллоха. Піттса Вид логістичної функції
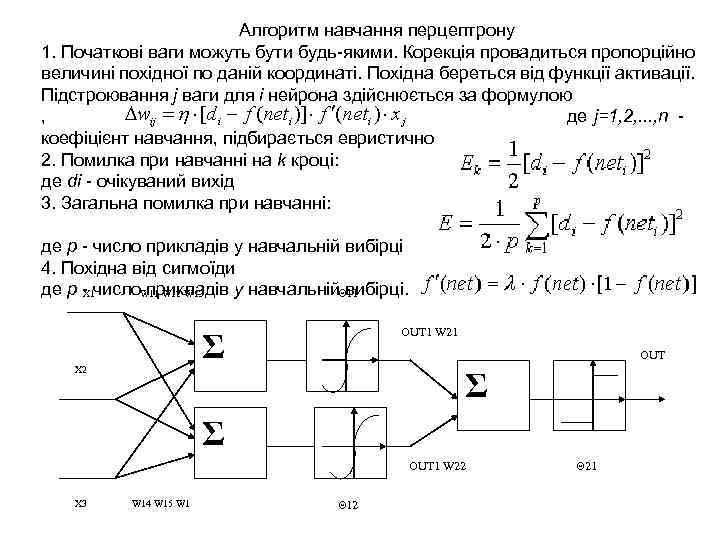Алгоритм навчання перцептрону 1. Початкові ваги можуть бути будь-якими. Корекція провадиться пропорційно величині похідної по даній координаті. Похідна береться від функції активації. Підстроювання j ваги для i нейрона здійснюється за формулою , де j=1, 2, . . . , n - коефіцієнт навчання, підбирається евристично 2. Помилка при навчанні на k кроці: де di - очікуваний вихід 3. Загальна помилка при навчанні: де p - число прикладів у навчальній вибірці 4. Похідна від сигмоїди де p - число прикладів у навчальній вибірці. X 1 W 11 W 12 W 13 Θ 11 X 2 OUT 1 W 21 Σ OUT Σ Σ OUT 1 W 22 X 3 W 14 W 15 W 1 Θ 12 Θ 21
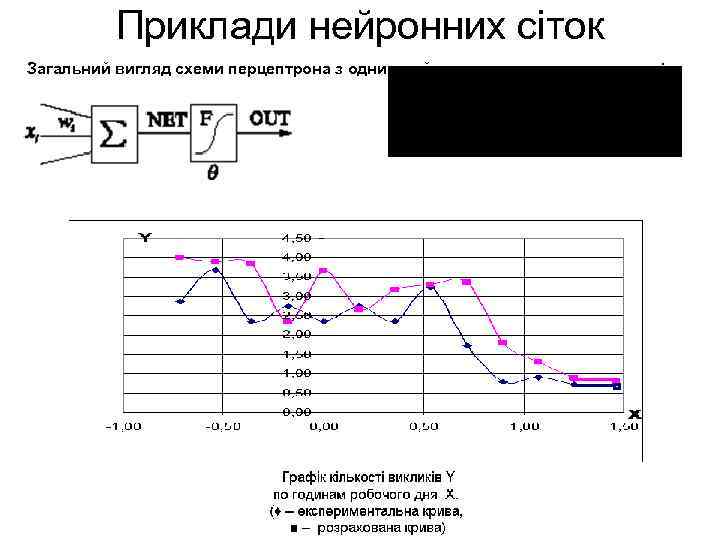Приклади нейронних сіток Загальний вигляд схеми перцептрона з одним нейроном та суматором на вході
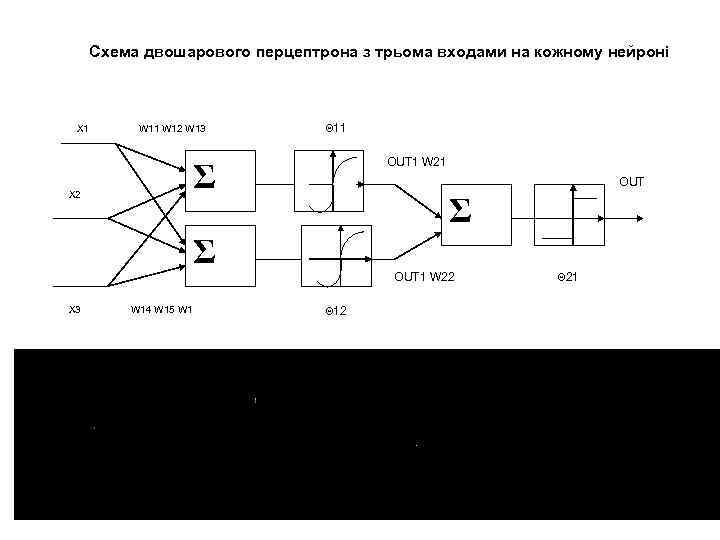Схема двошарового перцептрона з трьома входами на кожному нейроні X 1 W 11 W 12 W 13 X 2 Θ 11 OUT 1 W 21 Σ OUT Σ Σ OUT 1 W 22 X 3 W 14 W 15 W 1 Θ 12 Θ 21
ОЦІНКА ЯКОСТІ АПРОКСИМАЦІЇ ТА ПРОГНОЗУВАННЯ
Оцінка адекватності апроксимації та якості прогнозування 1. Для перевірки адекватності апроксимації проводиться розрахунок вихідних значень математичної моделі, підставляючи в неї реальні вхідні значення, за якими ця модель була побудована. Для визначення якості прогнозування в модель підставляються ті значення вхідних факторів, які не було використано при розрахунках коефіцієнтів моделі. 2. Для кожної пари розрахованих у. Пі та реальних у. Рі значень розраховується критерій «хі-квадрат» за формулою 3. Визначається число ступенів свободи як r = n - 2. 4. Знаходиться теоретичне значення «хі-квадрат» за наперед визначеною довірчою ймовірністю. Ця довірча ймовірність має бути достатньо високою, щоб дослідник міг довіряти отриманим результатам (0, 8 -0, 99). Якщо це значення більше розрахованого, модель вважається адекватною з визначеною довірчою ймовірністю. В іншому випадку – модель не адекватна, тобто, погано описує процес. Якість прогнозування теж розуміється з цією довірчою ймовірністю.
Синтез динамічних моделей Просте запізнювання Часто вживана модель Дискретні моделі запізнювання
Нечіткі моделі Функція приналежності A = {x/m. A(x)>0}. Типи функцій приналежності Трикутна Трапецевидна в інших випадках Гаусіана Кругова
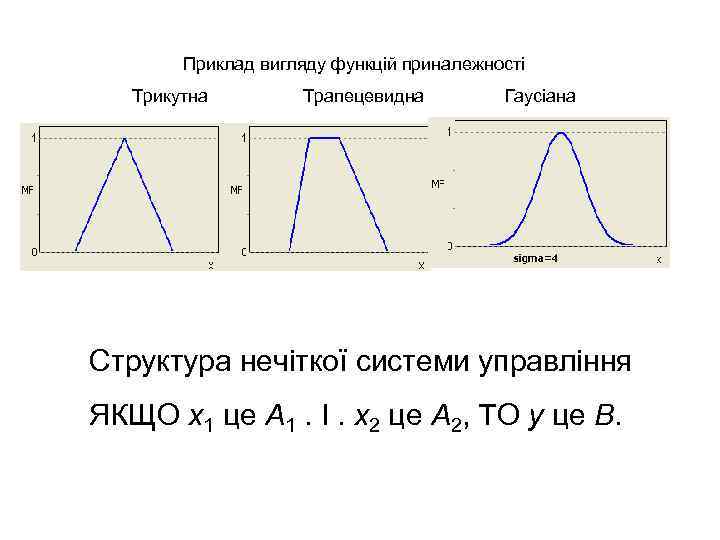Приклад вигляду функцій приналежності Трикутна Трапецевидна Гаусіана Структура нечіткої системи управління ЯКЩО x 1 це A 1. І. x 2 це A 2, ТО у це B.
ТЕОРІЯ ОПТИМАЛЬНИХ СИСТЕМ ТА ЇЇ ЗАСТОСУВАННЯ В ОПТИМІЗАЦІЇ ПРОЦЕСІВ УПРАВЛІННЯ В ЕКОНОМІЦІ
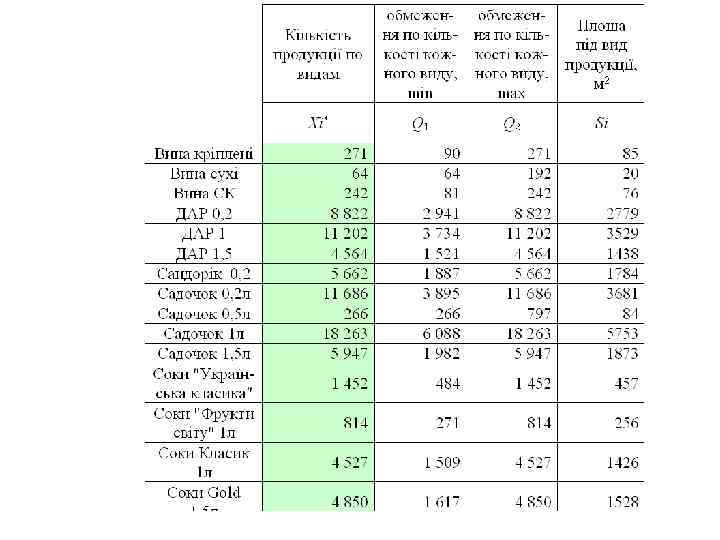
ПРИКЛАД ПОБУДОВИ ОПТИМІЗАЦІЙНОЇ ЗАДАЧІ Ціна товарної продукції: телевізор – 180 у. о. , відеомагнітофон – 260 у. о. , музичний центр - 420 у. о. Собівартість складається з витрат на оренду площі – 4000 у. о. , витрат на комплектуючі – 100, 170, 315 відповідно на випуск одного телевізора, відеомагнітофона та музичного центру; інших витрат – 4500 у. о. Необхідна зарплата інженерів складає 400, директора - 600, робітників на конвеєрі - 350. Для підприємства нашого масштабу необхідно 3 директори незалежно від випуску і 1 на кожні 150 одиниць продукції. Необхідно 1 -2 інженери на кожні 150 одиниць випуску продукції. Фонд заробітної платні, обмежений через податкові проблеми у 260, 5 млн. у. о. Всього в наявності є 230 місць, кожне з яких займає 7, 4 квадратних метрів, враховуючи проходи до них. Необхідно також розвернути мінімум 10 робочих місць для інженерів, кожне з яких займає 8, 5 квадратних метрів. Загальна площа виробничих приміщень становить 2000 квадратних метрів. Площа, необхідна для розміщення готової продукції кожного виду становить: 0, 3 - для телевізорів, що випускаються за місяць; 0, 35 - для відеомагнітофонів, що випускаються за місяць; 0, 4 – для музичних центрів, що випускаються за місяць.
Оптимізація типова постановка задачі
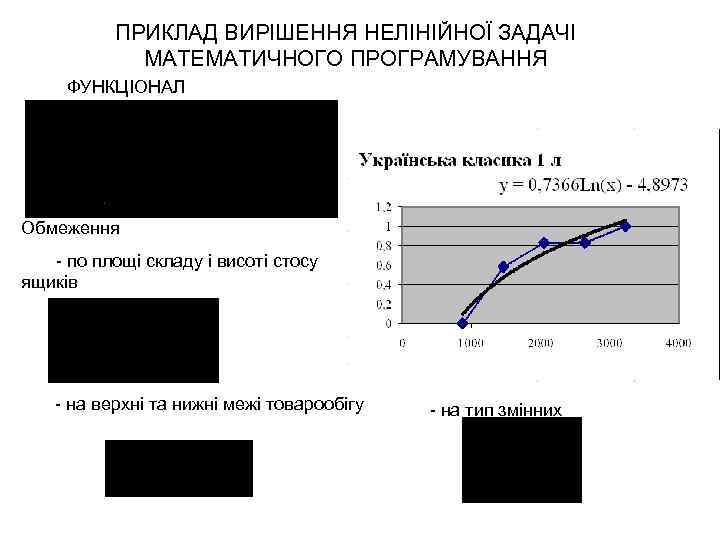ПРИКЛАД ВИРІШЕННЯ НЕЛІНІЙНОЇ ЗАДАЧІ МАТЕМАТИЧНОГО ПРОГРАМУВАННЯ ФУНКЦІОНАЛ Обмеження - по площі складу і висоті стосу ящиків - на верхні та нижні межі товарообігу - на тип змінних
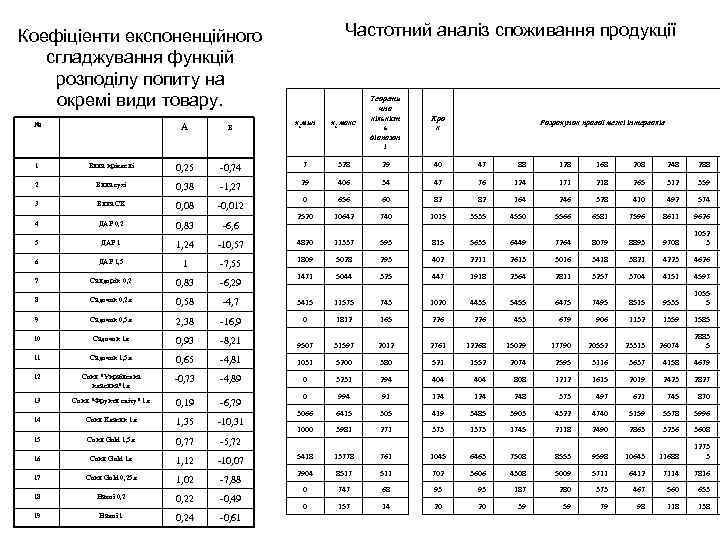Частотний аналіз споживання продукції Коефіціенти експоненційного сгладжування функцій розподілу попиту на окремі види товару. А № в хі мин хі макс Теорети чна кількіст ь діапазон і Кро к Розрахунок правої межі інтервалів 1 Вина кріплені 0, 25 -0, 74 7 328 29 40 47 88 128 168 208 248 288 2 Вина сухі 0, 38 -1, 27 29 406 34 47 76 124 171 218 265 312 359 3 Вина СК 0, 08 -0, 012 0 656 60 82 82 164 246 328 410 492 574 4 ДАР 0, 2 0, 83 -6, 6 2520 10642 740 1015 3535 4550 5566 6581 7596 8611 9626 5 ДАР 1 1, 24 -10, 57 4820 11337 593 815 5635 6449 7264 8079 8893 9708 1052 3 6 ДАР 1, 5 1 -7, 55 1809 5028 293 402 2211 2613 3016 3418 3821 4223 4626 7 Сандорік 0, 2 0, 83 -6, 29 1471 5044 325 447 1918 2364 2811 3257 3704 4151 4597 8 Садочок 0, 2 л 0, 58 -4, 7 3415 11575 743 1020 4435 5455 6475 7495 8515 9535 1055 5 9 Садочок 0, 5 л 2, 38 -16, 9 0 1812 165 226 453 679 906 1132 1359 1585 10 Садочок 1 л 0, 93 -8, 21 9507 31597 2012 2761 12268 15029 17790 20552 23313 26074 2883 5 11 Садочок 1, 5 л 0, 65 -4, 81 1031 5200 380 521 1552 2074 2595 3116 3637 4158 4679 12 Соки "Українська класика"1 л -0, 73 -4, 89 0 3231 294 404 808 1212 1615 2019 2423 2827 13 Соки "Фрукти світу" 1 л 0, 19 -6, 79 0 994 91 124 248 373 497 621 745 870 14 Соки Класик 1 л 1, 35 -10, 31 3066 6415 305 419 3485 3903 4322 4740 5159 5578 5996 1000 3981 271 373 1745 2118 2490 2863 3236 3608 15 Соки Gold 1, 5 л 0, 77 -5, 72 16 Соки Gold 1 л 1, 12 -10, 07 5418 13778 761 1045 6463 7508 8553 9598 10643 11688 1273 3 17 Соки Gold 0, 25 л 1, 02 -7, 88 2904 8517 511 702 3606 4308 5009 5711 6412 7114 7816 18 Напої 0, 22 -0, 49 0 747 68 93 93 187 280 373 467 560 653 0 157 14 20 20 39 59 79 98 118 138 19 Напої 1 0, 24 -0, 61
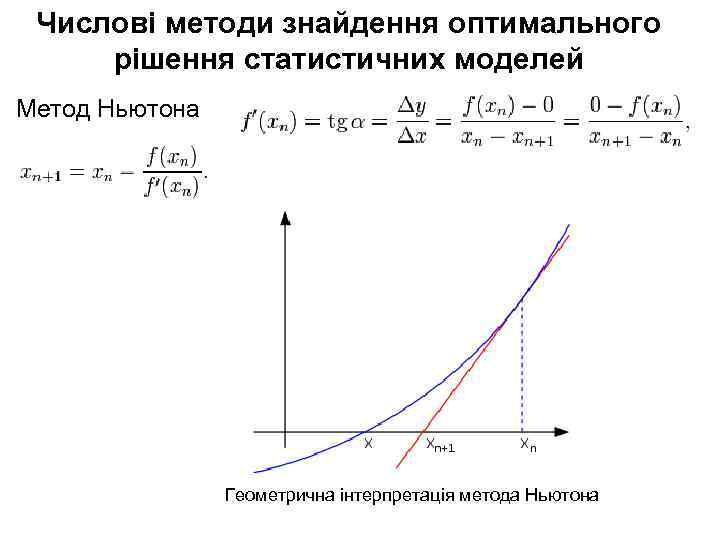Числові методи знайдення оптимального рішення статистичних моделей Метод Ньютона Геометрична інтерпретація метода Ньютона
Метод зв'язаних градієнтів Формально порядок розрахунку наступний: 1. Задаються початковим наближенням і погрішністю: 2. Розраховують початковий напрям: 3. Якщо або то , то розрахунок закінчено, потрібна точність досягнута. 4. Інакше якщо то і перехід до п. 3; 5. інакше і перехід до п. 2.
ТРАНСПОРТНА ЗАДАЧА
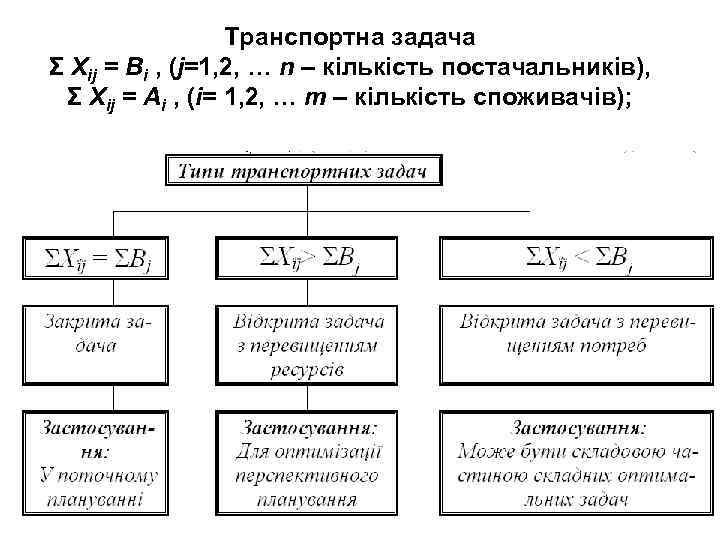Транспортна задача Σ Хij = Bi , (j=1, 2, … n – кількість постачальників), Σ Хij = Ai , (i= 1, 2, … m – кількість споживачів);
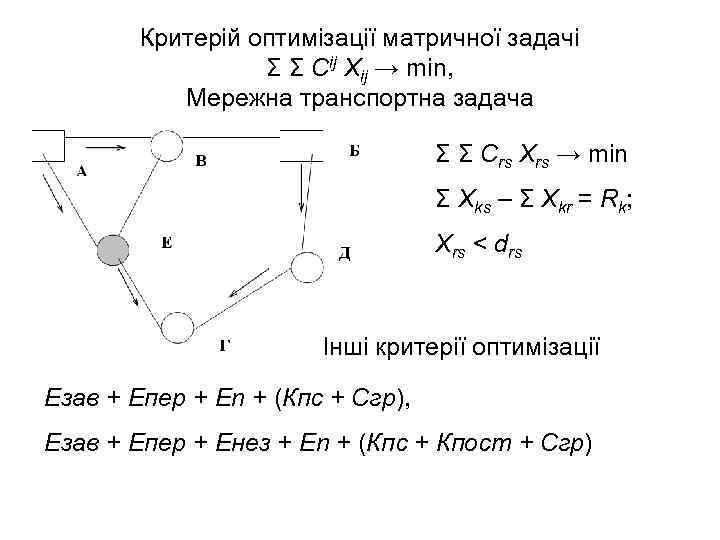Критерій оптимізації матричної задачі Σ Σ Сij Хij → min, Мережна транспортна задача Σ Σ Сrs Хrs → min Σ Xks – Σ Xkr = Rk; Хrs < drs Інші критерії оптимізації Езав + Епер + Еn + (Кпс + Cгр), Езав + Епер + Енез + Еn + (Кпс + Кпост + Cгр)
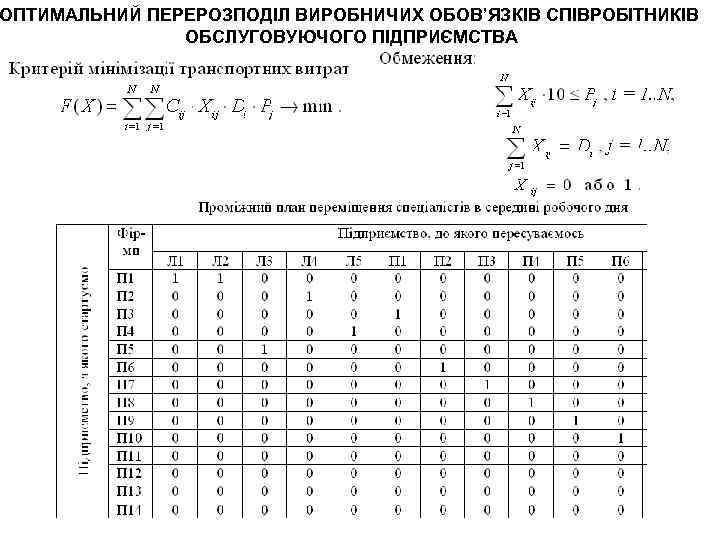ОПТИМАЛЬНИЙ ПЕРЕРОЗПОДІЛ ВИРОБНИЧИХ ОБОВ’ЯЗКІВ СПІВРОБІТНИКІВ ОБСЛУГОВУЮЧОГО ПІДПРИЄМСТВА
Багатокритеріальні задачі Формальне визначення -оптимальності рішення х, записується як вимога про відсутність такого рішення х Dx, при якому б були виконані умови і хоча б одне з них – строго (зі знаком >).
Зведення до задачі математичного програмування Метод гарантованого результату
Метод згортки часткових критеріїв
ТЕОРІЯ ІГОР Антагоністична гра
Кооперативна (біматрична) гра
Ігри з природою Прийняття рішень при відомих ймовірностях стану природи
Ігри з природою в умовах повної невизначеності Критерії максимакса Максимінний критерій Вальда Критерій мінімаксного ризику Севіджа Критерій песимізму-onmимізму Гурвіца
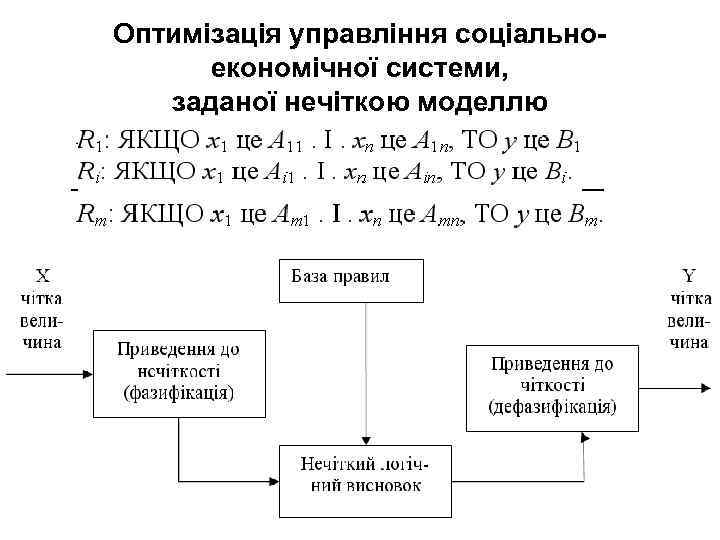Оптимізація управління соціальноекономічної системи, заданої нечіткою моделлю
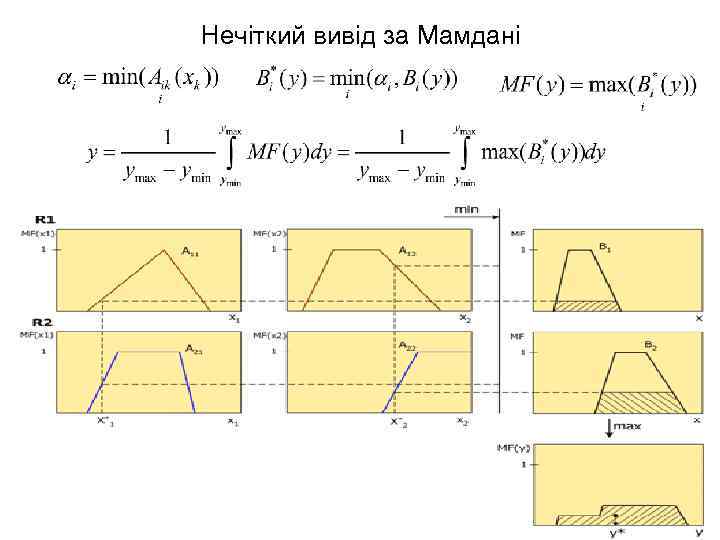Нечіткий вивід за Мамдані