Эйлеровы графы Эйлеровым путём графа G V E называется

Эйлеровы графы. Эйлеровым путём графа G(V, E) называется такой путь, такой, что каждое ребро появляется в нём ровно 1 раз. Граф G(V, E) называется эйлеровым, если он имеет замкнутый эйлеров путь (эйлеров цикл), и полуэйлеровым, если эйлеров путь, не являющийся замкнутым, но содержащий все вершины по 1 разу.

ТЕОРЕМА (критерий эйлеровости графа): связный граф G является эйлеровым тогда и только тогда, когда каждая вершина G имеет чётную степень. Доказательство: Пусть Р – эйлеров цикл в графе G. Тогда при каждом прохождении цикла через вершину графа используется одно ребро для входа и одно ребро для выхода. Поскольку каждое ребро используется 1 раз, то каждая вершина должна иметь чётную степень.

Обратно. Индукцией по числу рёбер в графе. Базис индукции: каждая компонента связности графа имеет эйлеров цикл. Докажем, что весь граф имеет эйлеров цикл. Пусть граф G связен и степень каждой вершины чётна. Если степень каждой вершины не меньше 2, то граф имеет цикл. Следовательно граф содержит цикл С. Если С содержит каждое ребро, то теорема доказана.

Если нет, то удаляем из графа G все рёбра, принадлежащие циклу С. Получаем новый граф G 1, возможно несвязный. Число рёбер в G 1 меньше, чем в G, и каждая вершина имеет чётную степень. По предположению индукции, в каждой компоненте графа G 1 имеется эйлеров цикл. В силу связности графа G каждая компонента графа G 1 имеет общие вершины с циклом С.

Проходим рёбра G следующим образом: идём по рёбрам цикла С до первой неизолированной вершины графа G 1. Затем проходим эйлеров цикл в компоненте графа G 1, затем снова двигаемся по циклу С до следующей неизолированной вершины графа G 1. Процесс закончится в исходной вершине, что и показывает существование эйлерова цикла.

Алгоритм построения эйлерова пути в эйлеровом графе: Теорема: Пусть G – эйлеров граф. Тогда следующая процедура всегда возможна и приводит к построению эйлеровой цепи графа G. Выходя из произвольной вершины, идём по рёбрам графа произвольным образом, соблюдая следующие правила: • Стираем рёбра по мере их прохождения (вместе с изолированными вершинами, которые при этом образуются); • На каждом этапе идём по ребру, удаление которого нарушает связность, только в том случае, когда нет других возможностей.

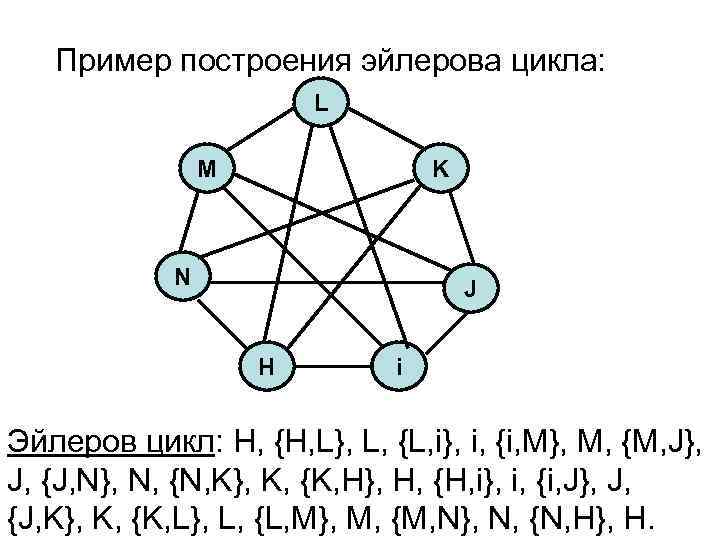Пример построения эйлерова цикла: L M K N J H i Эйлеров цикл: H, {H, L}, L, {L, i}, i, {i, M}, M, {M, J}, J, {J, N}, N, {N, K}, K, {K, H}, H, {H, i}, i, {i, J}, J, {J, K}, K, {K, L}, L, {L, M}, M, {M, N}, N, {N, H}, H.

Гамильтоновы графы. Граф называется гамильтоновым, если в нём существует цикл, проходящий ровно один раз через каждую вершину.

Теорема (Дирака): Если в графе G (V, E) с n вершинами (n 3) выполняется условие для v V. Тогда граф G является гамильтоновым. Доказательство: Заметим следующее. Если к любому графу G добавить некоторое количество новых вершин, соединяя каждую из них с каждой вершиной графа, то получим гамильтонов граф G/. Пусть добавили к графу минимальное число k новых вершин, k>0, после чего граф стал гамильтоновым.

Рассмотрим гамильтонов цикл v 1, w, v 2, …, v 1 в графе G/, где vi V, w – одна из новых вершин. Следовательно, v 2 не является смежной с v 1 в графе G/, поскольку тогда можно не использовать вершину w, что противоречило бы минимальности числа k. Далее, пусть вершина v 2/ смежная с v 2, а v 1/ смежная с v 1. Тогда v 2/ не может следовать за v 1/ в цикле. Действительно, в этом случае цикл v 1, w, v 2, …, v 1/, v 2/ , …, v 1 можно заменить на v 1, v 1/, …, v 2/ , …, v 1 и снова высвободить вершину w.

Значит, число вершин графа G/, не являющихся смежными с v 2, не меньше числа вершин, смежных с v 1, поскольку на гамильтоновом цикле за любой вершиной, смежной с v 1, следует вершина не смежная с v 2. Число вершин, смежных с v 1, не меньше, чем (n/2)+k, то же и для вершины v 2. Далее, поскольку любая вершина графа G/ является либо смежной, либо не смежной вершине v 2, то значит общее число вершин n+k не меньше, чем Полученное противоречие показывает, что k=0, т. е. Исходный граф гамильтонов.