Эйлерова характеристика и числа Бетти3.pptx
- Количество слайдов: 33

ЭЙЛЕРОВА ХАРАКТЕРИСТИКА И ЧИСЛА БЕТТИ Выполнили: Зейнолла Айбар Сыздыков Ербол

* Главная цель научной работы исследовать инварианты различных геометрических объектов, а именно эйлерову характеристику * Актуальность проекта состоит в том. что везде, где можно моделировать практическую задачу при помощи комплексов, подсчитав числа Бетти и эйлерову характеристику, можно определить возможность получения из одного объекта другой объект. То есть числа Бетти и эйлерова характеристика имеют практическое важное применение не только для чисто математических задач, решаемых с помощью моделирования комплексами.

* Каждое семейство прямых разбивает плоскость на части, называемые гранями разбиения; их число будем обозначать Г. Вершинами разбиения называются точки пересечения данных прямых, а ребрами разбиения - части, на которые прямые делятся вершинами. *Теорема В - Р + Г = 1, где В - число вершин, Р число ребер , Г – число граней
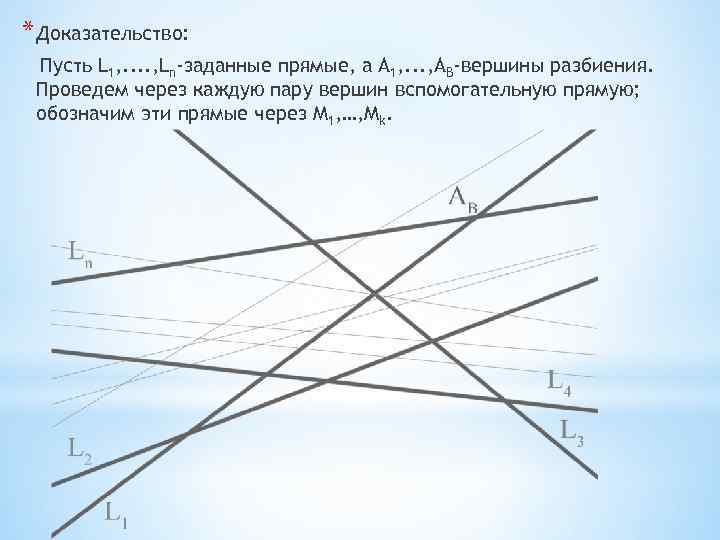
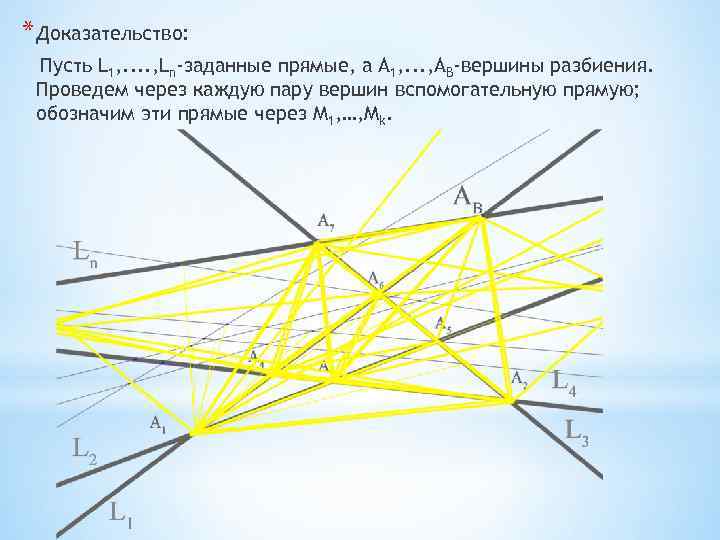
* Доказательство: Пусть L 1, . . , Ln-заданные прямые, а А 1, . . . , AB-вершины разбиения. Проведем через каждую пару вершин вспомогательную прямую; обозначим эти прямые через М 1, …, Мk.
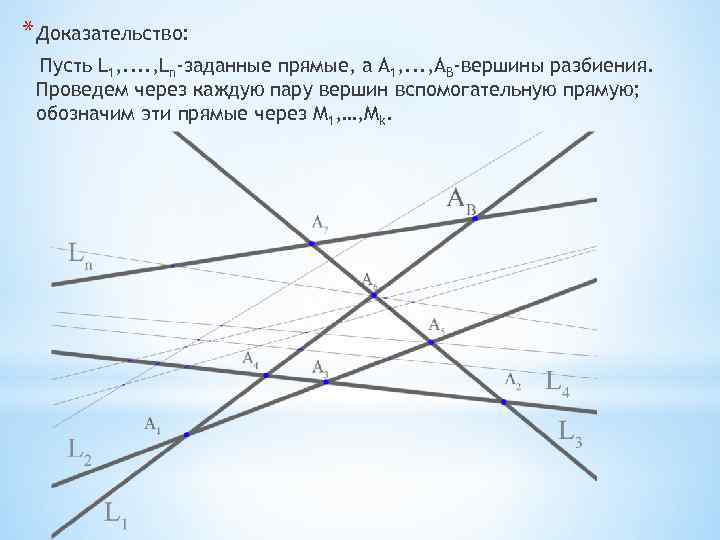
* Доказательство: Пусть L 1, . . , Ln-заданные прямые, а А 1, . . . , AB-вершины разбиения. Проведем через каждую пару вершин вспомогательную прямую; обозначим эти прямые через М 1, …, Мk.
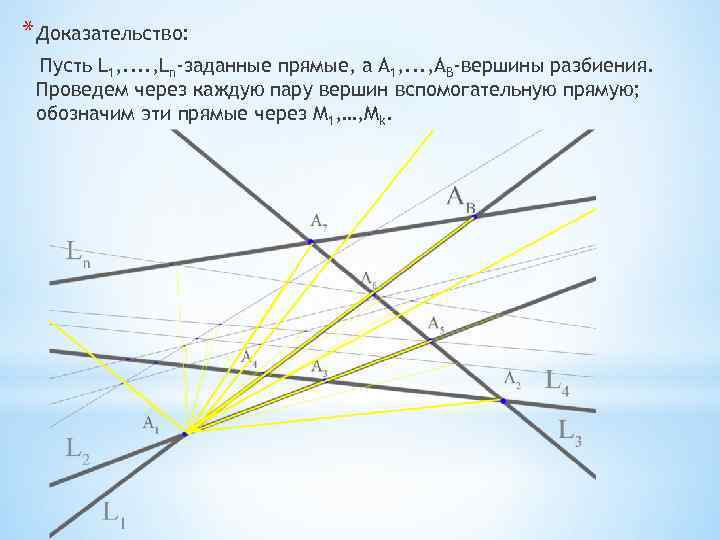
* Доказательство: Пусть L 1, . . , Ln-заданные прямые, а А 1, . . . , AB-вершины разбиения. Проведем через каждую пару вершин вспомогательную прямую; обозначим эти прямые через М 1, …, Мk.
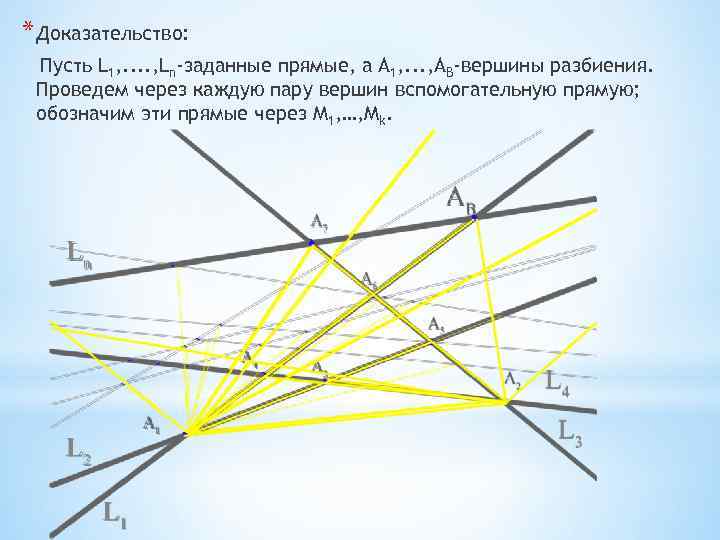
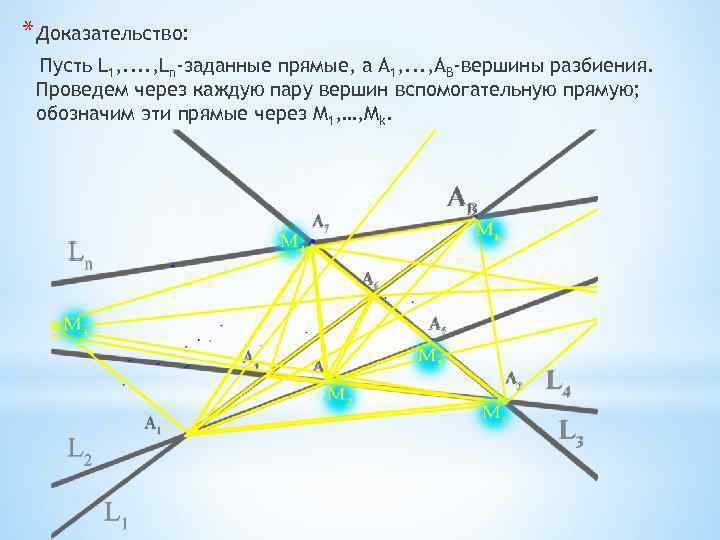
* Доказательство: Пусть L 1, . . , Ln-заданные прямые, а А 1, . . . , AB-вершины разбиения. Проведем через каждую пару вершин вспомогательную прямую; обозначим эти прямые через М 1, …, Мk.
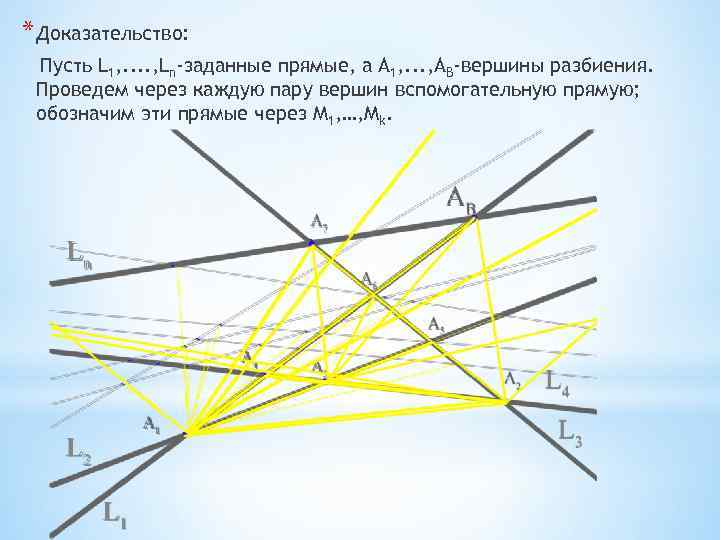
* Доказательство: Пусть L 1, . . , Ln-заданные прямые, а А 1, . . . , AB-вершины разбиения. Проведем через каждую пару вершин вспомогательную прямую; обозначим эти прямые через М 1, …, Мk.
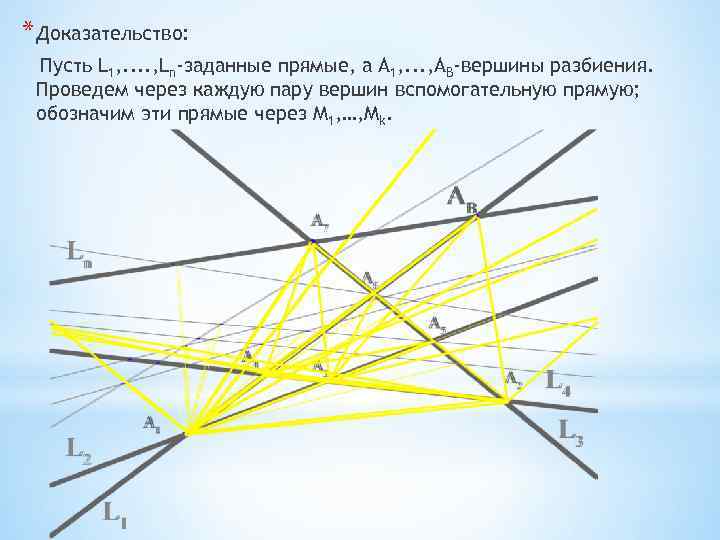
* Доказательство: Пусть L 1, . . , Ln-заданные прямые, а А 1, . . . , AB-вершины разбиения. Проведем через каждую пару вершин вспомогательную прямую; обозначим эти прямые через М 1, …, Мk.
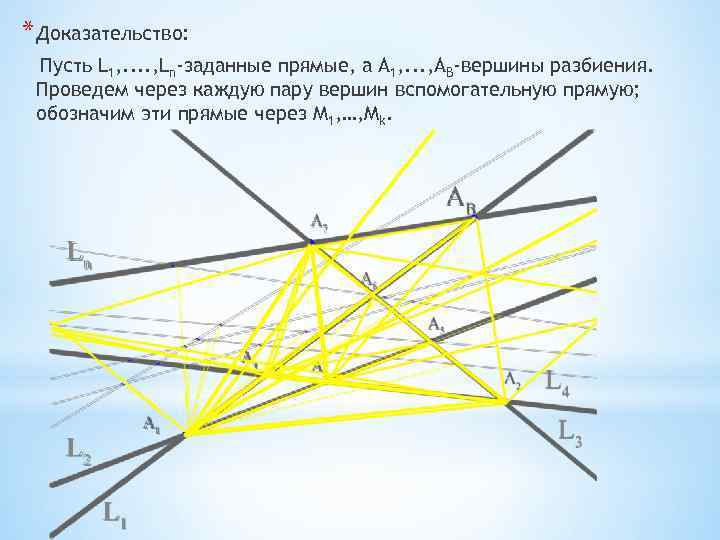
* Доказательство: Пусть L 1, . . , Ln-заданные прямые, а А 1, . . . , AB-вершины разбиения. Проведем через каждую пару вершин вспомогательную прямую; обозначим эти прямые через М 1, …, Мk.
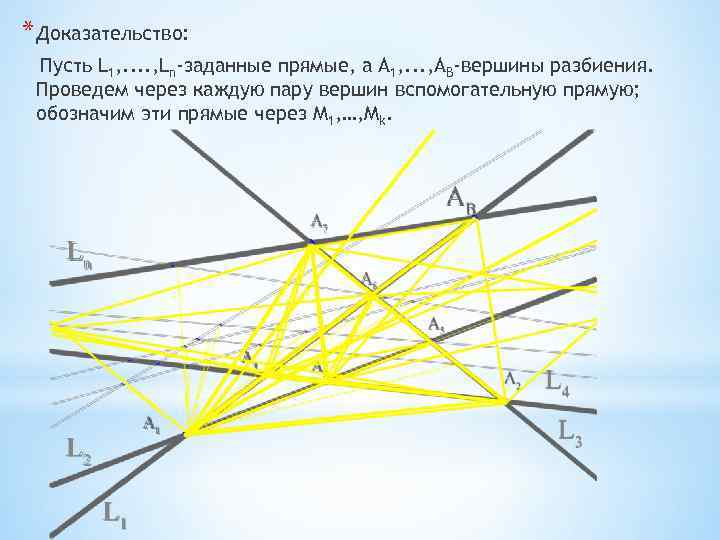
* Доказательство: Пусть L 1, . . , Ln-заданные прямые, а А 1, . . . , AB-вершины разбиения. Проведем через каждую пару вершин вспомогательную прямую; обозначим эти прямые через М 1, …, Мk.
* Доказательство: Пусть L 1, . . , Ln-заданные прямые, а А 1, . . . , AB-вершины разбиения. Проведем через каждую пару вершин вспомогательную прямую; обозначим эти прямые через М 1, …, Мk.
* Доказательство: Пусть L 1, . . , Ln-заданные прямые, а А 1, . . . , AB-вершины разбиения. Проведем через каждую пару вершин вспомогательную прямую; обозначим эти прямые через М 1, …, Мk.
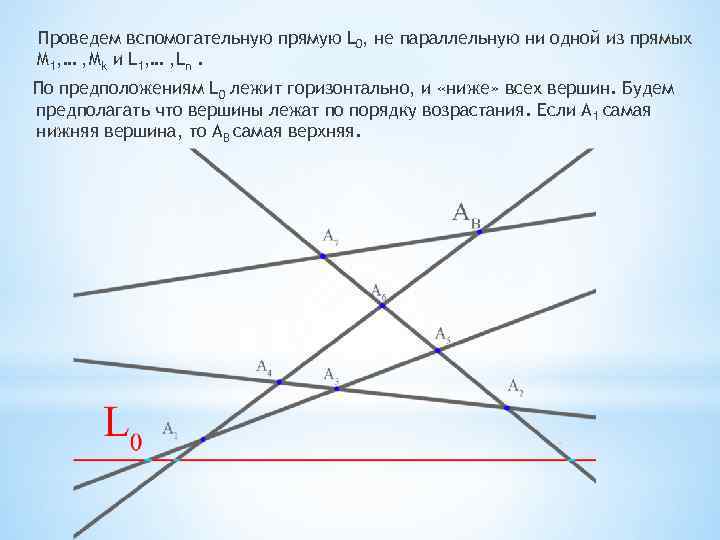
Проведем вспомогательную прямую L 0, не параллельную ни одной из прямых М 1, … , Мk и L 1, … , Ln. По предположениям L 0 лежит горизонтально, и «ниже» всех вершин. Будем предполагать что вершины лежат по порядку возрастания. Если А 1 самая нижняя вершина, то AB самая верхняя.
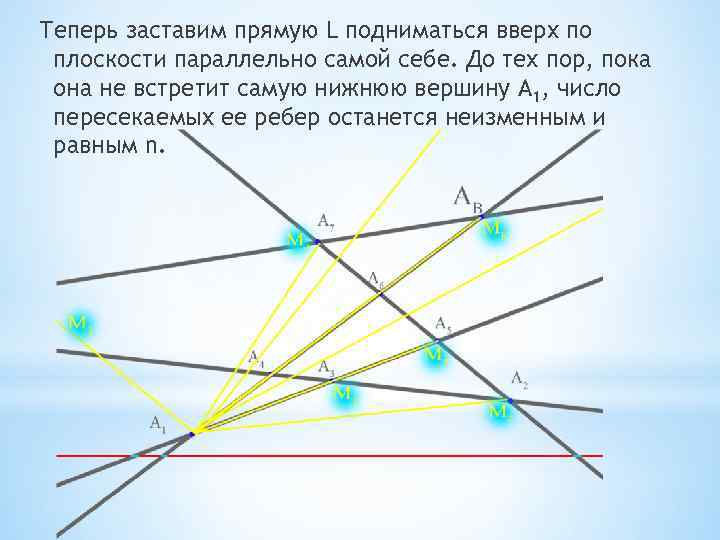
Теперь заставим прямую L подниматься вверх по плоскости параллельно самой себе. До тех пор, пока она не встретит самую нижнюю вершину А 1, число пересекаемых ее ребер останется неизменным и равным n.
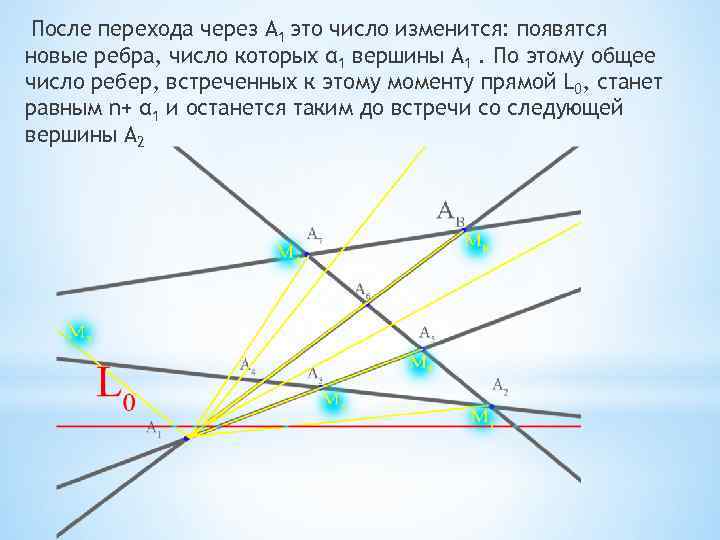
После перехода через А 1 это число изменится: появятся новые ребра, число которых α 1 вершины А 1. По этому общее число ребер, встреченных к этому моменту прямой L 0, станет равным n+ α 1 и останется таким до встречи со следующей вершины А 2
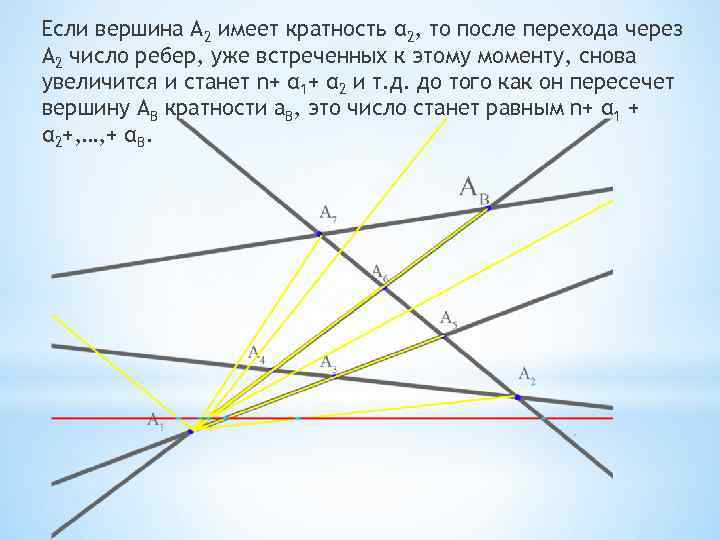
Если вершина А 2 имеет кратность α 2, то после перехода через А 2 число ребер, уже встреченных к этому моменту, снова увеличится и станет n+ α 1+ α 2 и т. д. до того как он пересечет вершину АB кратности а. B, это число станет равным n+ α 1 + α 2+, …, + αB.
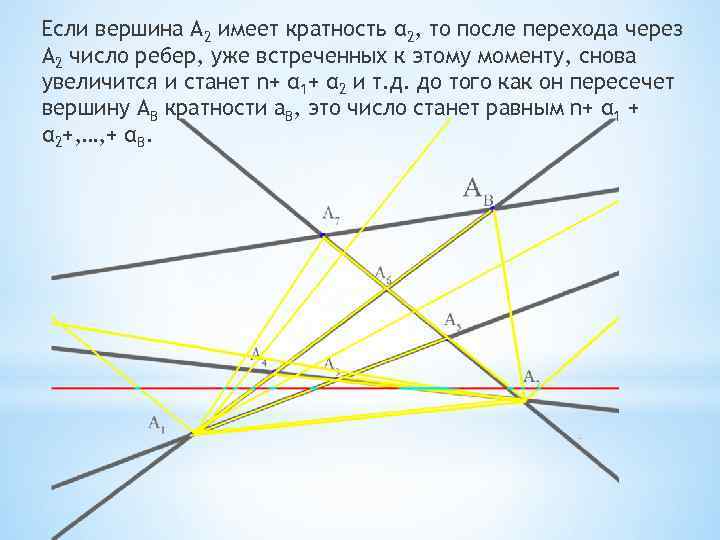
Если вершина А 2 имеет кратность α 2, то после перехода через А 2 число ребер, уже встреченных к этому моменту, снова увеличится и станет n+ α 1+ α 2 и т. д. до того как он пересечет вершину АB кратности а. B, это число станет равным n+ α 1 + α 2+, …, + αB.
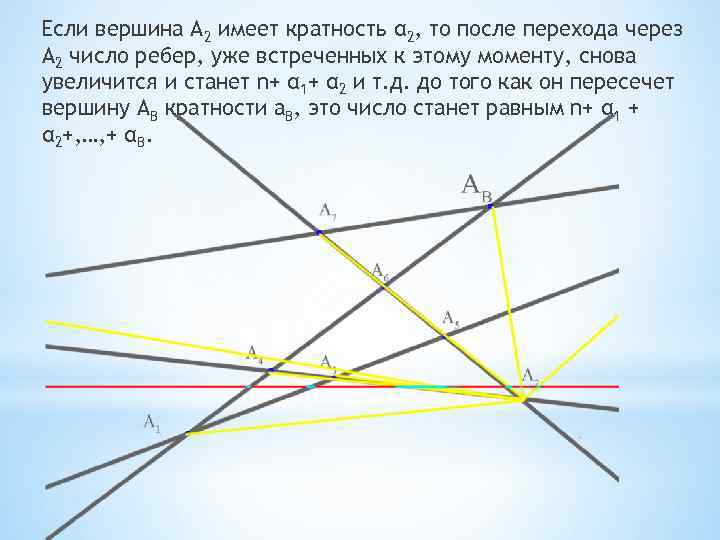
Если вершина А 2 имеет кратность α 2, то после перехода через А 2 число ребер, уже встреченных к этому моменту, снова увеличится и станет n+ α 1+ α 2 и т. д. до того как он пересечет вершину АB кратности а. B, это число станет равным n+ α 1 + α 2+, …, + αB.
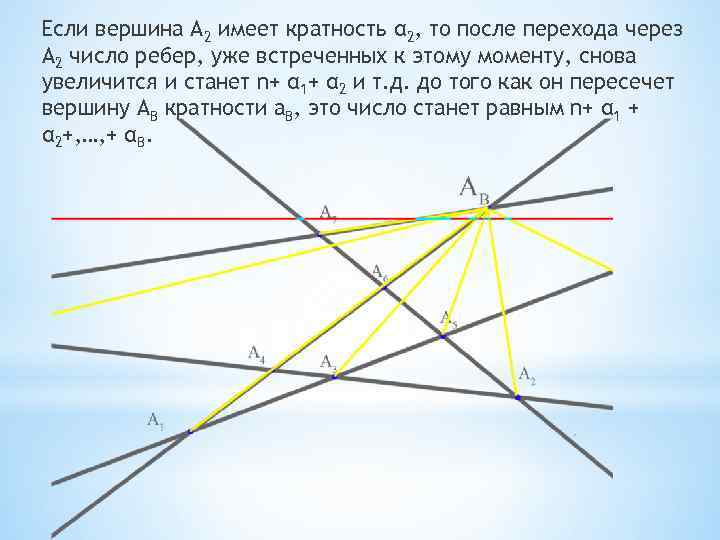
Если вершина А 2 имеет кратность α 2, то после перехода через А 2 число ребер, уже встреченных к этому моменту, снова увеличится и станет n+ α 1+ α 2 и т. д. до того как он пересечет вершину АB кратности а. B, это число станет равным n+ α 1 + α 2+, …, + αB.

Поэтому:
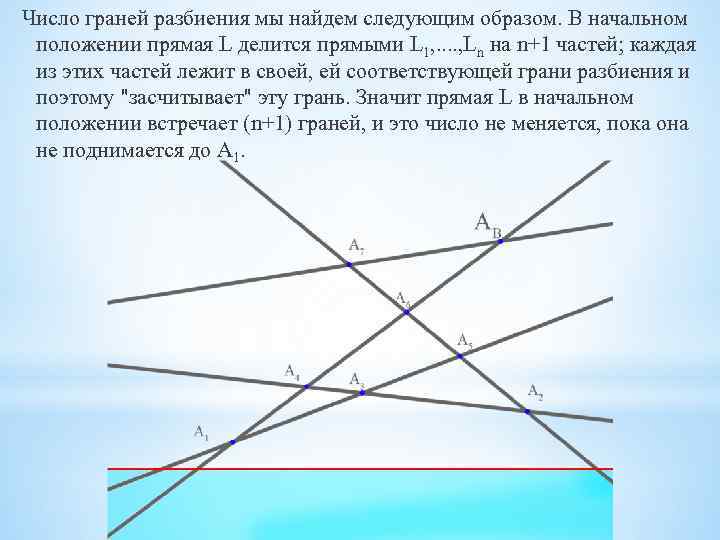
Число граней разбиения мы найдем следующим образом. В начальном положении прямая L делится прямыми L 1, . . , Ln на n+1 частей; каждая из этих частей лежит в своей, ей соответствующей грани разбиения и поэтому "засчитывает" эту грань. Значит прямая L в начальном положении встречает (n+1) граней, и это число не меняется, пока она не поднимается до А 1.
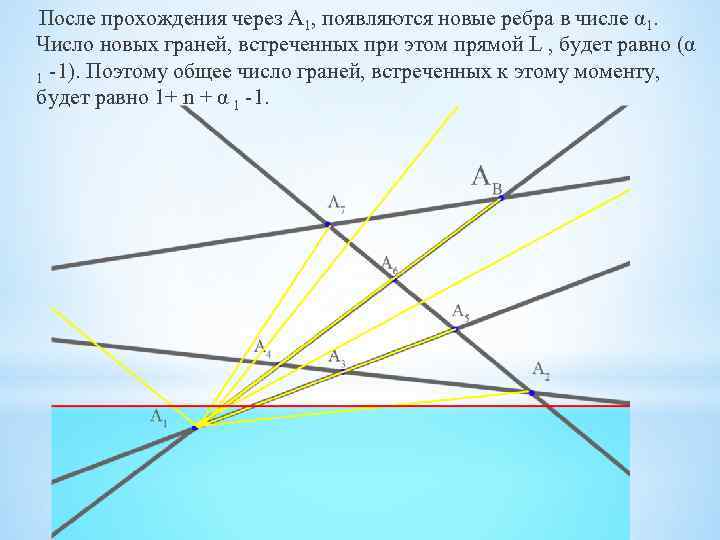
После прохождения через А 1, появляются новые ребра в числе α 1. Число новых граней, встреченных при этом прямой L , будет равно (α 1 -1). Поэтому общее число граней, встреченных к этому моменту, будет равно 1+ n + α 1 -1.
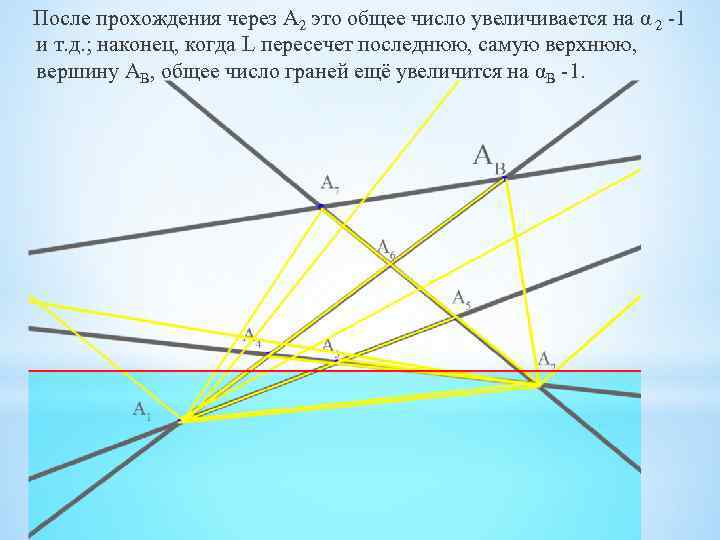
После прохождения через А 2 это общее число увеличивается на α 2 -1 и т. д. ; наконец, когда L пересечет последнюю, самую верхнюю, вершину АB, общее число граней ещё увеличится на αB -1.
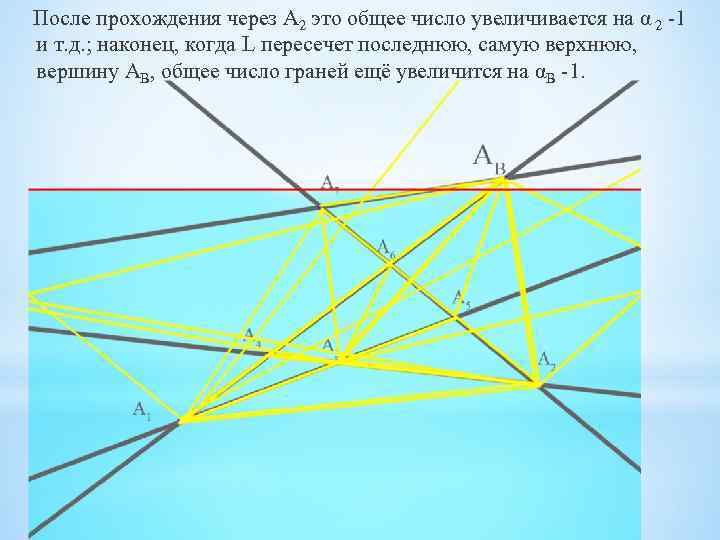
После прохождения через А 2 это общее число увеличивается на α 2 -1 и т. д. ; наконец, когда L пересечет последнюю, самую верхнюю, вершину АB, общее число граней ещё увеличится на αB -1.
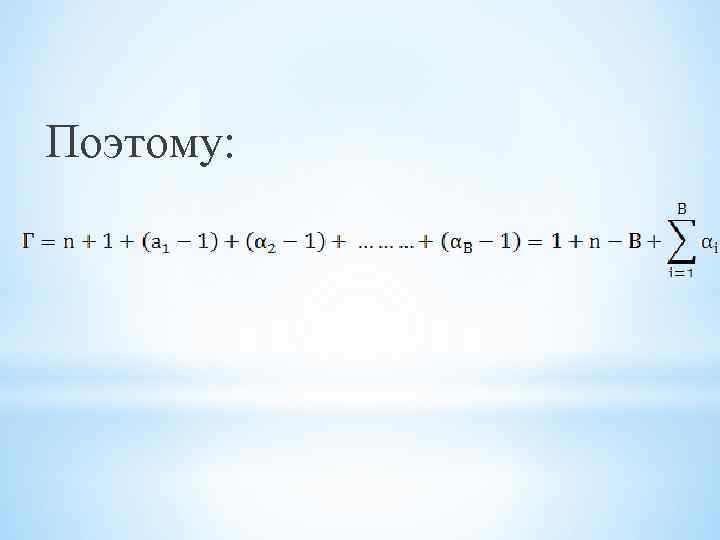
Поэтому:

В итоге мы получаем числа разбиения ребер и граней. Наконец мы вставляем ее в формулу В-Р+Г=1, что бы её доказать.

* Многоугольником называется плоская фигура М, состоящая из объединения конечного числа выпуклых многоугольников так, что выполнены следующие два условия: 1. Любые два выпуклые многоугольника либо совсем не имеют общих точек, либо имеют только общую вершину, либо имеют общую сторону. 2. Фигура М связна, т. е. любые две её точки можно соединить простой незамкнутой ломаной, целиком лежащей в М. * Под разбиением многоугольника на клетки следует понимать, что гранями разбиения будем называть те выпуклые многоугольники, из которых составлен многоугольник М, ребра-стороны этих выпуклых многоугольников, вершины разбиения-их вершины. * Многоугольник называется простым, если его граница состоит из одного контура * Теорема : Эйлерова характеристика простого многоугольника равна 1.
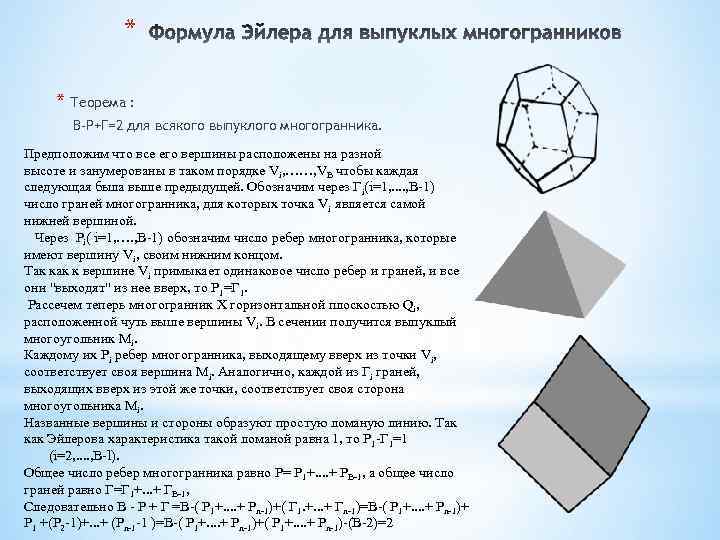
* * Теорема : В-Р+Г=2 для всякого выпуклого многогранника. Предположим что все его вершины расположены на разной высоте и занумерованы в таком порядке Vi, ……, VB чтобы каждая следующая была выше предыдущей. Обозначим через Гi(і=1, . . , В-1) число граней многогранника, для которых точка Vi является самой нижней вершиной. Через Pi( і=1, …. , В-1) обозначим число ребер многогранника, которые имеют вершину Vi, своим нижним концом. Так к вершине Vi примыкает одинаковое число ребер и граней, и все они "выходят" из нее вверх, то P 1=Г 1. Рассечем теперь многогранник X горизонтальной плоскостью Qi, расположенной чуть выше вершины Vi. В сечении получится выпуклый многоугольник Мi. Каждому их Рi ребер многогранника, выходящему вверх из точки Vi, соответствует своя вершина Мi. Аналогично, каждой из Гi граней, выходящих вверх из этой же точки, соответствует своя сторона многоугольника Мi. Названные вершины и стороны образуют простую ломаную линию. Так как Эйлерова характеристика такой ломаной равна 1, то Р 1 -Г 1=1 (i=2, . . , B-l). Общее число ребер многогранника равно Р= P 1+. . + РB-1, а общее число граней равно Г=Г 1+. . . + ГB-1, Следовательно В - Р + Г =В-( Р 1+. . + Рn-1)+( Г 1. +. . . + Гn-1)=В-( Р 1+. . + Рn-1)+ Р 1 +(Р 2 -1)+. . . + (Рn-1 -1 )=В-( Р 1+. . + Рn-1)+( Р 1+. . + Рn-1)-(В-2)=2

* Определение: Множество с операцией сложения +: Gx. G→G называется группой, если 1) ∀a, b, c ∈G (a+b)+c=a+(b+c) 2) ∃! 0∈G т. ч. ∀a∈G а+0 = 0+а=а 3) ∀ a ∈G ∃(-а) ∈G, т. ч а+(-а) =(-а)+а=0 Если кроме того выполнено условие коммутативности: 4) ∀a, B ∈G a+b = b+a то G называется абелевой группой. Далее в нашей работе мы рассматриваем только абелевы группы. Н ⊂G Н называется подгруппой G, если 1. ∀ h 1, h 2, ∈ Н ⇒ h 1+ h 2 ∈ H 2. ∀ h ∈ H⇒ (-h) ∈ Н Левым смежным классом G по подгруппе Н с * * Представителем а называется множество = { а + h, где h ∈ Н } которое обозначается а + Н Если G - абелева, то для любой подгруппе Н можно определить новую группу, называемой факторгруппой и обозначаемой G/H. Элементами G/H являются левые смежные классы G по Н с операцией сложения: (а+ H)+(b+H) (а+ b)+Н

* а 0 , а 1, а 2, а 3 - система независимых точек пространства R 3 А 3 ={х ∈R|х= λ 0 а 0+ λ 1 а 1+ λ 2 а 2 + λ 3 а 3, λ 0+ λ 1 + λ 2+ λ 3 =1 и λ 0 ≥ 0, λ 1 ≥ 0, λ 2 ≥ 0 и λ 3 ≥ 0} называется 3 -мерным симплексом. Будем писать А 3 =( а 0, а 1, а 2, а 3). Исходные точки а 0, а 1, а 2, а 3 называются вершинами симплекса А 3 * Говорят, что симплексы А и В эвклидова пространства R 3 расположены правильно, если они или вовсе не пересекаются или их пересечение А⋂В является гранью каждого из симплексов А и В. Одномерными гранями А являются: (а 0, а 1), ( а 0, а 2), ( а 0, а 3), ( а 1, а 2), ( а 1, а 3), ( а 2, а 3) * Двумерными гранями А являются: (а 0, а 1, а 2), (а 0, а 2, а 3), (а 0, а 1, а 3), (а 1, а 2, а 3) Конечная совокупность К симплексов называется комплексом, если: • Наряду с каждым симплексом А совокупность К, в К входит также и любая грань симплекса А • Каждые два симплекса К расположены правильно 1. Подкомплекса К называется всякий комплекс L , все симплексы которого принадлежат К. 2. Связность : Комплекс К будем называть связным, если его невозможно разбить в сумму двух не пустых подкомплексов L и М без общих симплексов.

1, 2 - примеры комплексов 3, 4, 5 - не комплексы ( )

Заключение Мы разобрались с основами теории групп и использовали две фундаментальные теоремы, теорема о структуре конечно порожденных абелевых групп и теория о ранге группы, подгруппы и факторгруппы. Также мы ввели понятие симплекса и комплекса и использовали оператор взятия границы. С помощью данной теории ввели числа Бетти и доказали топологическую инвариантность Эйлеровой характеристики. С помощью триангуляции Вороного строится комплекс Делоне и считаются геометрические инварианты числа Бетти молекул протеина. С помощью чисел Бетти можно определить можно ли химическим путем получить из одного протеина другой.
Эйлерова характеристика и числа Бетти3.pptx