Efficient Reachability Analysis of Hierarchic Reactive Modules R

Efficient Reachability Analysis of Hierarchic Reactive Modules R. Alur, R. Grosu, M. Mc. Dougall University of Pennsylvania www. cis. upenn. edu/~alur, grosu, mmcdougall

Motivation Scalable analysis demands modular reasoning: • modeling language has to support syntactically and semantically modular constructs, • model checking has to exploit modular design. Close the gap between: • software design languages (UML, Statecharts, Rsml, …), • model checking languages (Spin, SMV, Mocha, …).

Talk Outline ü Motivation • • Mode diagrams From statecharts to mode diagrams Model checking Wrap-up

Mode Diagrams 1. Visual language for hierarchic reactive machines • • • hierarchic modes, mode sharing, group transitions, history, mixed and/or hierarchies. 2. Observational trace semantics • • mode refinement, modular reasoning. 3. Model checker • • exploits the hierarchy information, exploits the type information.

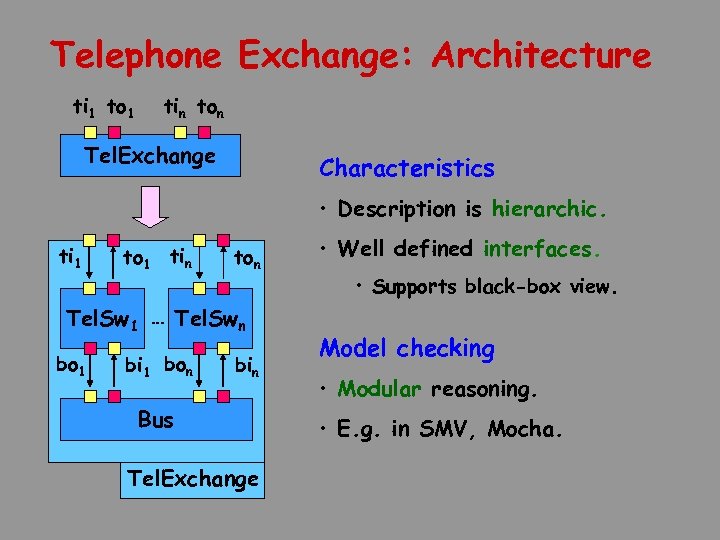
Telephone Exchange: Architecture ti 1 to 1 tin ton Tel. Exchange Characteristics • Description is hierarchic. ti 1 to 1 tin ton Tel. Sw 1 … Tel. Swn bo 1 bi 1 bon bin Bus Tel. Exchange • Well defined interfaces. • Supports black-box view. Model checking • Modular reasoning. • E. g. in SMV, Mocha.

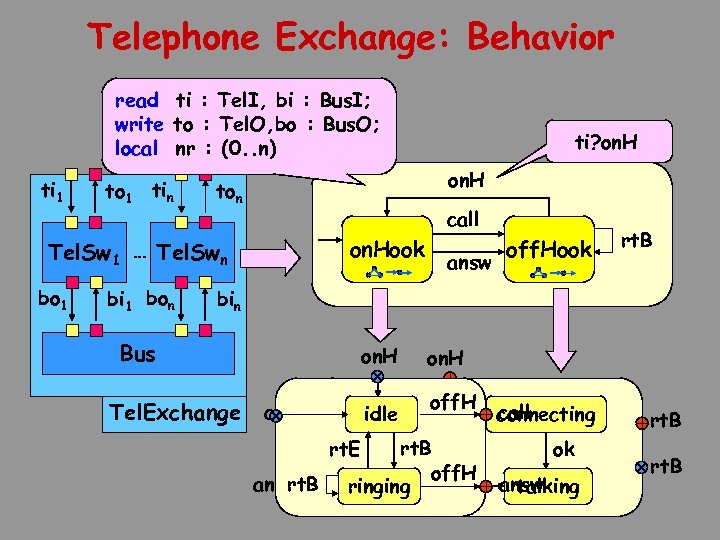
Telephone Exchange: Behavior read ti : Tel. I, bi : Bus. I; write to : Tel. O, bo : Bus. O; local nr : (0. . n) ti 1 to 1 tin on. H ton call on. Hook Tel. Sw 1 … Tel. Swn bo 1 bi 1 bon ti? on. H answ off. Hook rt. B bin Bus Tel. Exchange on. H call ok off. H call idle getting. No connecting rt. B off. H ringing rt. E answ rt. B on. H ok answ talking rt. B

Statecharts Formalism • Introduced: 1987 by David Harel, • Related notations: Rsml, Modecharts, Roomcharts, • Key component in OO Methods: UML, ROOM, OMT, etc. Difficulties • No denotational trace semantics (no refinement notion), • No scoping for variables. Previous attempts compile statecharts to flat diagrams.

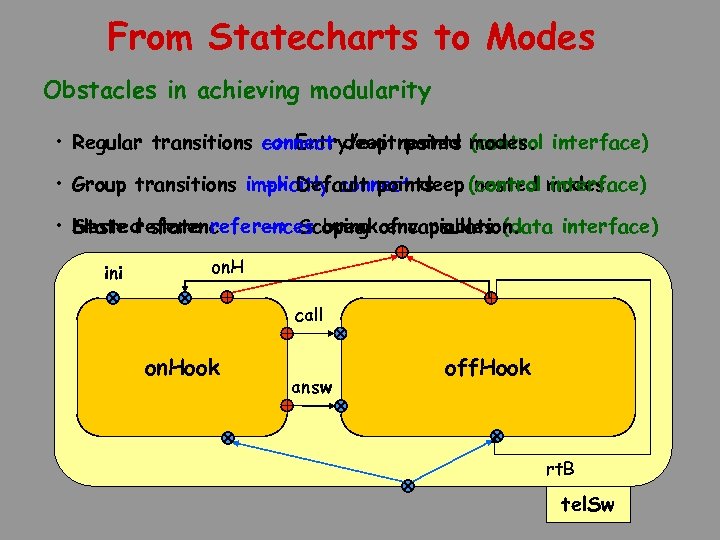
From Statecharts to Modes Obstacles in achieving modularity connect deep points (control • Regular transitions -> Entry/exitnested modes. interface) • Group transitions implicitly connect deep (control modes. -> Default points nested interface) • Nested state references break of variables (data interface) State reference -> Scoping encapsulation. H ini idle off. H rt. B on. Hook rt. E off. H rt. B ringing on. Hook on. H call answ getting. No ok connecting off. Hook ok talking off. Hook rt. B tel. Sw

Model Checking Graphical editor and both an enumerative and a symbolic model checker. Reachability analysis exploits the structure: • Reached state space indexed by control points, • Transition relation is indexed by control points, • Transition type exploited in mdd construction, • Mode definitions are shared among instances.

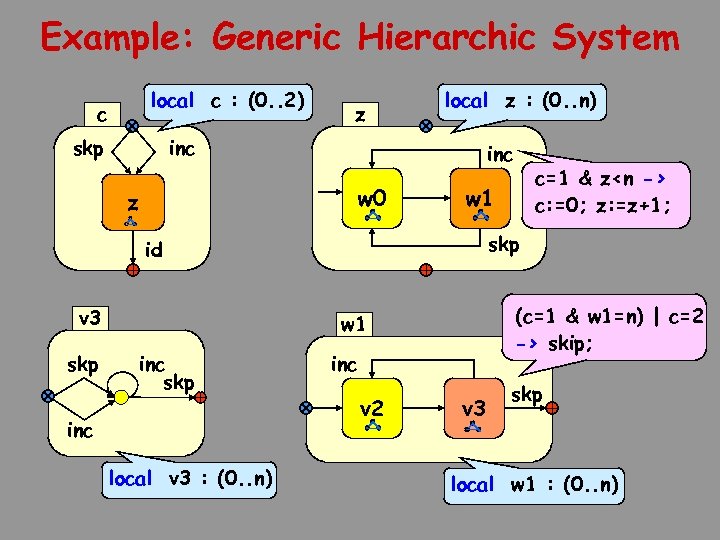
Example: Generic Hierarchic System local c : (0. . 2) c skp z local z : (0. . n) inc w 0 z w 1 skp id v 3 skp (c=1 & w 1=n) | c=2 -> skip; w 1 inc skp inc local v 3 : (0. . n) c=1 & z<n -> c: =0; z: =z+1; inc v 2 v 3 skp local w 1 : (0. . n)

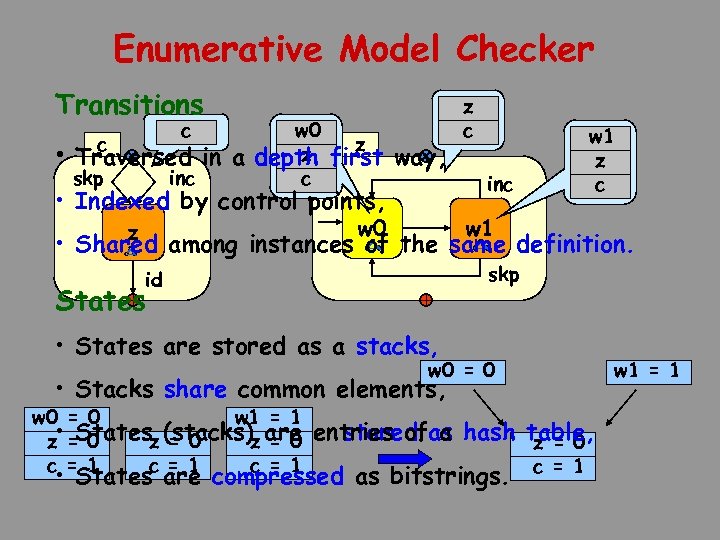
Enumerative Model Checker Transitions c c • Traversed in a skp inc w 0 z depth c z first way, • Indexed by control points, w 0 z z c inc w 1 z c w 1 • Shared among instances of the same definition. skp id States • States are stored as a stacks, w 0 = 0 • Stacks share common elements, w 0 = 0 w 1 = 1 z • =States (stacks) are 0 z = 0 c = 1 entries ofas hash table, stored a z = 0 • States are compressed as bitstrings. c = 1 w 1 = 1

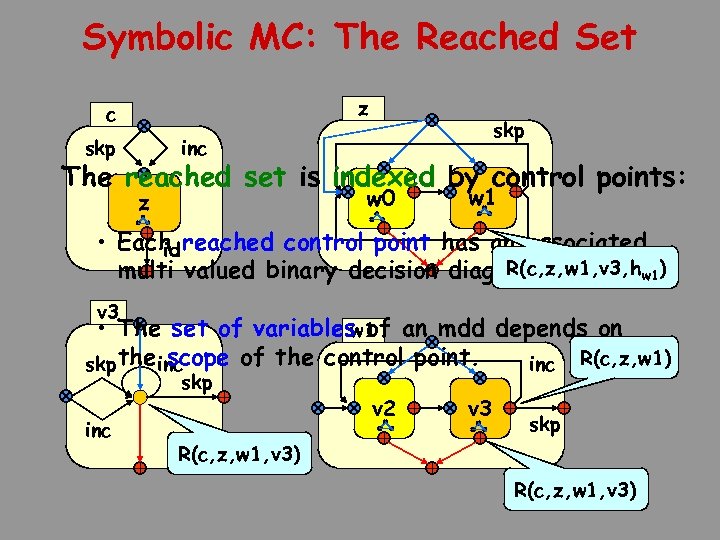
Symbolic MC: The Reached Set z c skp inc The reached set is indexed by control points: w 0 z w 1 • Each reached control point has an associated id inc R(c, z, w 1, v 3, h multi valued binary decision diagram (mdd), w 1) v 3 • The set of variables of an mdd depends on w 1 scope of the control point. inc R(c, z, w 1) skp the inc skp inc v 2 v 3 skp R(c, z, w 1, v 3)

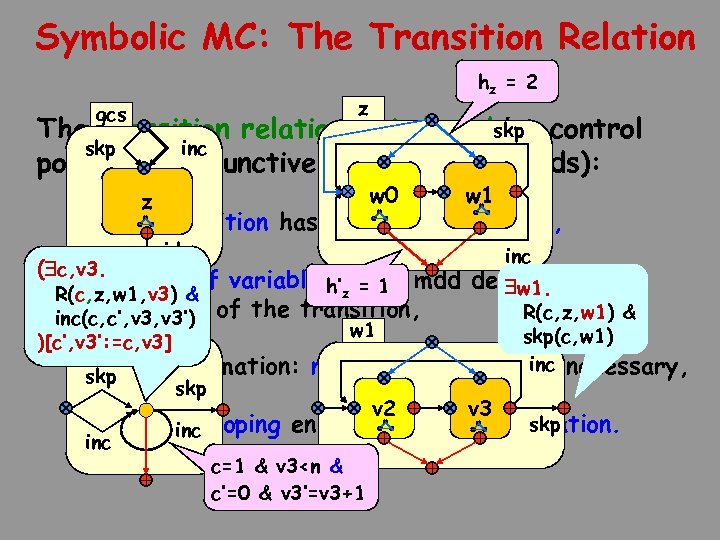
Symbolic MC: The Transition Relation hz = 2 z gcs The transition relation is indexedskp control by skp inc points (> conjunctively partitioned mdds): w 0 z w 1 • Each transition has an associated mdd, ( c, v 3. id inc • The set of variables z = an mdd depends on h’ of 1 w 1. R(c, z, w 1, v 3) & the scope R(c, z, w 1) & inc(c, c’, v 3’) of the transition, v 3 w 1 )[c’, v 3’: =c, v 3] • skp Type information: no identity skp v 2 skp(c, w 1) inc extension necessary, v 3 skp • Variable scoping enables early quantification. inc c=1 & v 3<n & c’=0 & v 3’=v 3+1

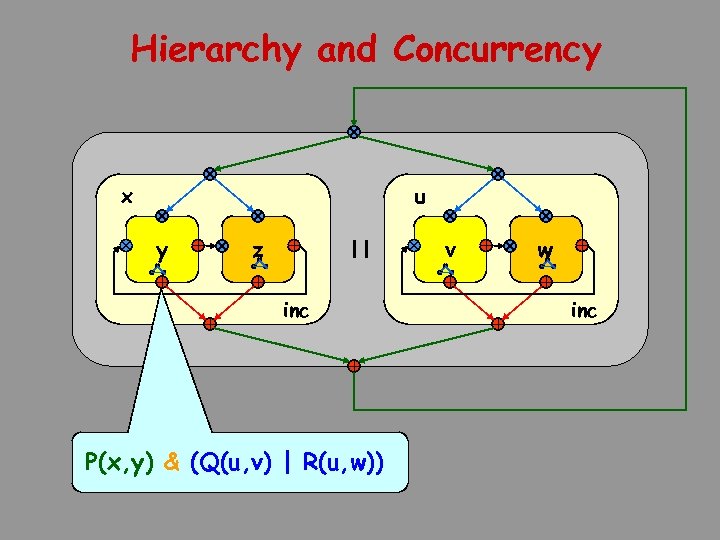
Hierarchy and Concurrency x u y z v inc P(x, y) & (Q(u, v) | R(u, w)) w inc

Results As expected, the model checker for modes is superior to current model checkers when: • sequential behavior is hierarchical, • modes have local variables.

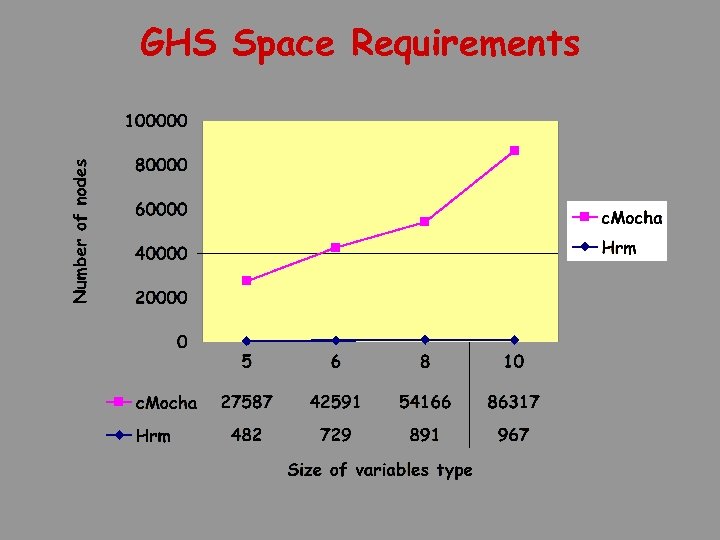
GHS Space Requirements

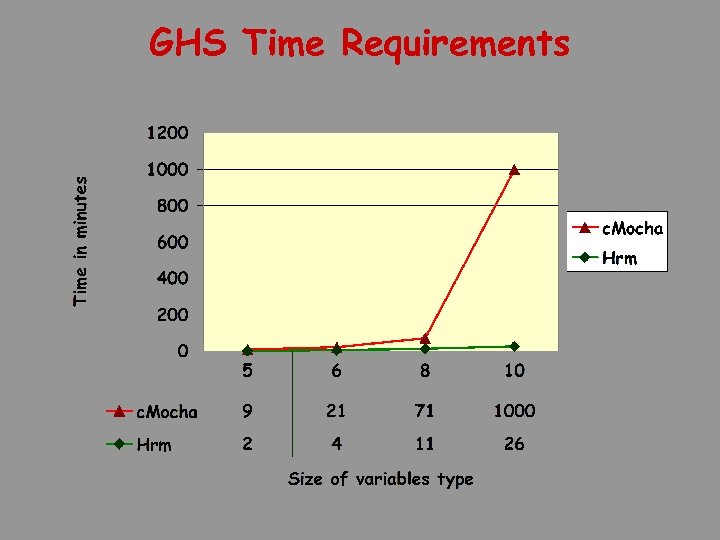
GHS Time Requirements

Project He. RMes Current status: • • visual language for behavior hierarchy, compositional semantics, modular refinement rules, model checking exploits hierarchic structure. Future work: • • • improve heuristics exploiting hierarchy, improve use of sharing, integrate/automate modular reasoning, collaboration with NEC on case studies, connection to Rational Rose/Objec. Time.

Demos at CAV j. Mocha v 2. 0 (released soon): • joint project U. C. Berkeley & UPenn, • a new version written in java, • several new features: • MSC-like simulator, proof manager, script language. He. RMes v 1. 0 (prototype): • developed at UPenn, • supports mode diagrams in this talk, Demos: • Tuesday morning, • Wednesday afternoon.

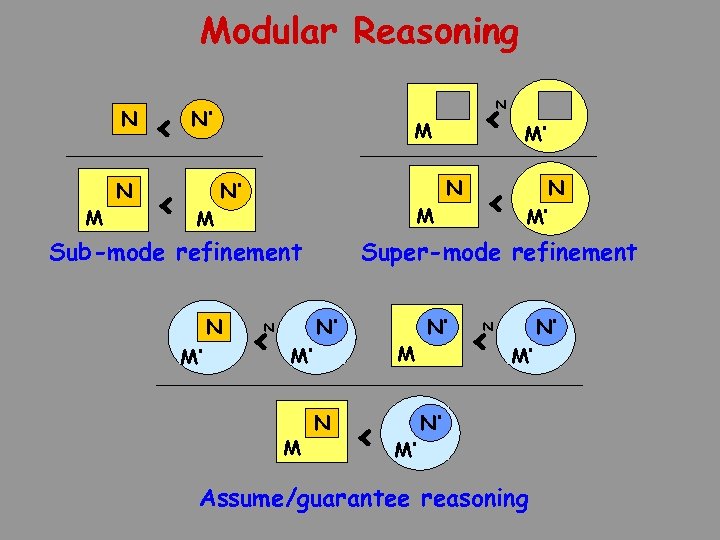
Modular Reasoning N M < N’ M M N N’ M Sub-mode refinement N M’ < N < M M’ M N M’ Super-mode refinement N’ N < M’ N’ < N’ N M’ N’ Assume/guarantee reasoning

A Macro Step A macro step is a breadth first traversal of the hierarchic mode graph starting at: • the default entry point of the top level mode and ending at: • the default exit point of the top level mode or • inside the mode if no new states are produced.

Semantics of Modes Game Semantics • Environment round: from exit points • Mode round: to entry points. from entry points to exit points. The set of traces of a mode • Constructed solely from the traces of the sub-modes and the mode’s transitions. Refinement • Defined as usual by inclusion of trace sets. • Is compositional w. r. t. mode encapsulation.

Modular Reasoning Terminology • Compositional and assume/guarantee reasoning based on observable behaviors. Application area • Only recently is being automated by model checkers, • Until now restricted to architecture hierarchies. Compositional Reasoning • Central to many formalisms: CCS, I/O Automata, TLA, etc. Circular Assume/Guarantee Reasoning • Valid only when the interaction of a module with its environment is non-blocking.

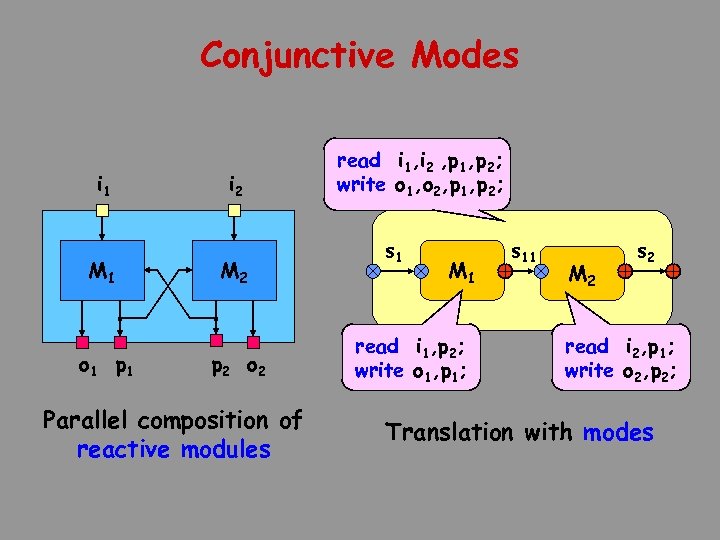
Conjunctive Modes Synchronous semantics i 1 M 1 o 1 p 1 i 2 M 2 p 2 o 2 Parallel composition of reactive modules read i , p , p ; 2 State o 1 , o , p 1 , p 2 ; write 1 2 s = (i 1, i 2, o 1, o 2, p 1, p 2) s 1 Execution M 1 s 11 syst read i 1, p 2; M 1 M write o 1, p 1; 2 M 2 syst read i , p ; M 1 M 22 1 write o 2, p 2; s 0 s 11 s 2 … sk sk 1 sk+1 Translation with modes env

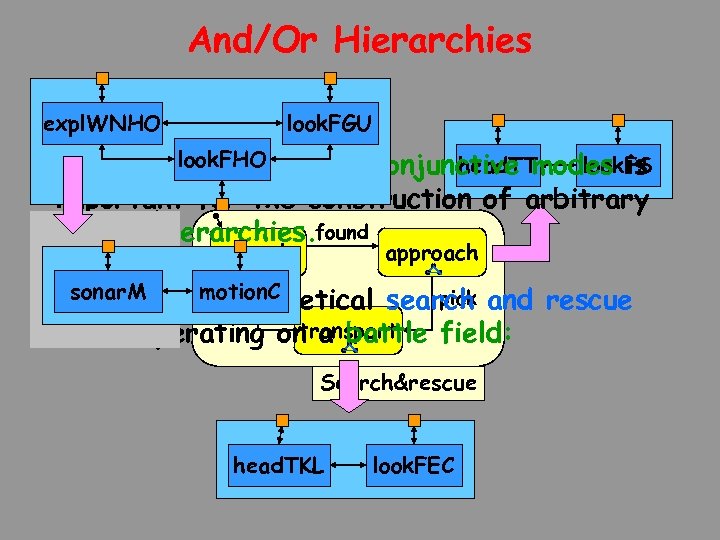
And/Or Hierarchies expl. WNHO look. FGU look. FHO head. TT look. FS The ability to express conjunctive modes is important for the construction of arbitrary and/or hierarchies. found search approach sonar. M done pick Consider a motion. C hypothetical search and rescue transport robot operating on a battle field: Search&rescue head. TKL look. FEC

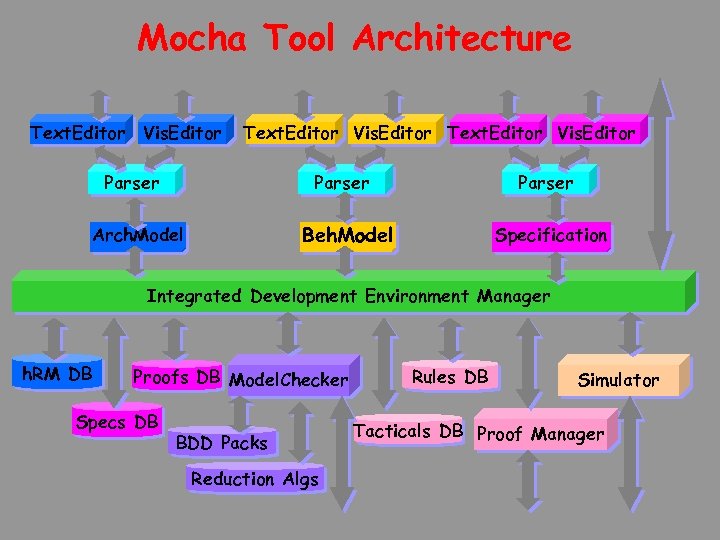
Mocha Tool Architecture Text. Editor Vis. Editor Parser Beh. Model Arch. Model Specification Integrated Development Environment Manager h. RM DB Proofs DB Model. Checker Specs DB BDD Packs Reduction Algs Rules DB Simulator Tacticals DB Proof Manager

Wrap-up Consider differential equations for activities: • • • Hybrid hierarchic modes, Avionics, robotics, automotive industry. Global and modular symulation, Exploit hierarchy in analysis, Relate to hybrid sequence diagrams. • Activity Diagrams Behavioral View