Efficient Processing of Top-k Spatial Preference Queries João

Efficient Processing of Top-k Spatial Preference Queries João B. Rocha-Junior, Akrivi Vlachou, Christos Doulkeridis, and Kjetil Nørvåg www. ntnu. no VLDB’ 2011 - Seattle, USA 1

Outline • Top-k spatial preference queries • Current approaches • Our approach – Mapping to distance-score space – Query processing – Materialization (index construction) • Experimental evaluation • Conclusion www. ntnu. no VLDB’ 2011 - Seattle, USA 2

Motivation • Increasing number of Web information systems specialized in location-based queries • Systems are limited to simple spatial queries – Example: return objects in a given spatial location • Top-k spatial preference query – Ranks data objects based on the score of feature objects in their spatial neighborhood – Combines spatial and non-spatial scores www. ntnu. no VLDB’ 2011 - Seattle, USA 3

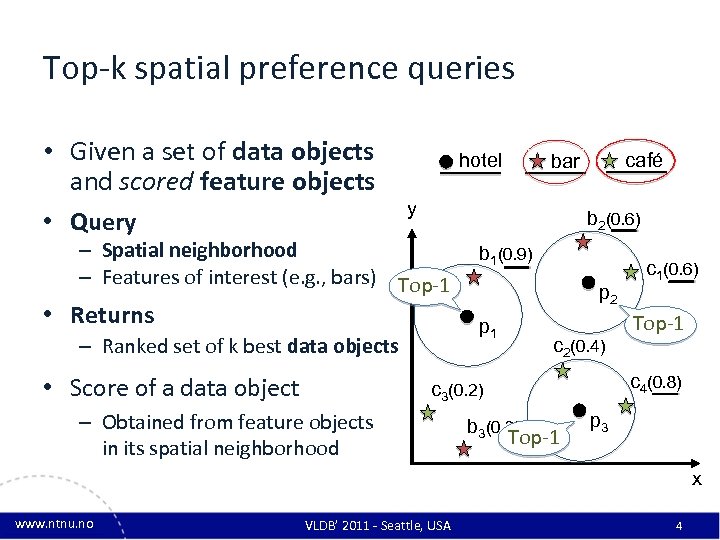Top-k spatial preference queries • Given a set of data objects and scored feature objects • Query hotel y b 2(0. 6) – Spatial neighborhood – Features of interest (e. g. , bars) Top-1 • Returns b 1(0. 9) p 2 p 1 – Ranked set of k best data objects • Score of a data object café bar c 2(0. 4) Top-1 c 4(0. 8) c 3(0. 2) – Obtained from feature objects in its spatial neighborhood c 1(0. 6) b 3(0. 3) Top-1 p 3 x www. ntnu. no VLDB’ 2011 - Seattle, USA 4

Score function • Aggregation of partial scores – Any monotone function: sum, max, and min • Partial score – Score of a data object for a set of feature objects – Defined by the score of a single feature object • Highest score • Satisfies the spatial constraint • Spatial constraint – Range, nearest neighbor, and influence www. ntnu. no VLDB’ 2011 - Seattle, USA 5

Example (agg=sum) Range score(p)=1. 5 www. ntnu. no Nearest neighbor score(p)=1. 0 VLDB’ 2011 - Seattle, USA Influence score(p)=0. 6 6

Current approaches • Naïve – Compute the score of all objects, select the top-k – Very costly • State-of-the-art [1, 2] – Data objects and feature objects are indexed by multi-dimensional indices [1] Yiu, M. L. , Dai, X. , Mamoulis, N. , Vaitis, M. , : “Top-k spatial preference queries”, ICDE, 2007. [2] Yiu, M. L. , Lu, H. , Mamoulis, N. , Vaitis, M. : “Ranking spatial data by quality preferences”, TKDE, 2011. www. ntnu. no VLDB’ 2011 - Seattle, USA 7

Current approaches • Probing algorithms (SP and GP) – Requires computing the score for all objects • Branch and bound algorithms (BB and BB*) – Compute an upper-bound score for the entries in the data objects R-tree – Prune entries whose upper-bound score is smaller than the score of the k-th object found • Feature join algorithm (FJ) – Create combinations of feature sets with high score – Combinations whose score is smaller than the score of the k-th object found are pruned www. ntnu. no VLDB’ 2011 - Seattle, USA 8

Motivation behind our idea… • Few feature objects are necessary to compute the score of a data object y c 2(0. 6) c 1(0. 5) – Features not dominated by any other feature in terms of both distance and score p 1 ? c 4(0. 4) c 3(0. 2) • Nice properties c 5(0. 8) x hotel www. ntnu. no – Small size in practice – Sufficient to support any neighborhood condition and query parameter café VLDB’ 2011 - Seattle, USA 9

Our framework • Mapping to distance-score space – Pairs of objects (p, t) with t Fi to be examined • Identify SKY(p, Fi) – Minimum set of pairs required to compute the score of p according to Fi for any query • Materialize SKY(p, Fi) – Stored in a R-tree, one R-tree Ri per feature set Fi – Efficient query processing and maintenance • Query processing algorithm www. ntnu. no VLDB’ 2011 - Seattle, USA 10

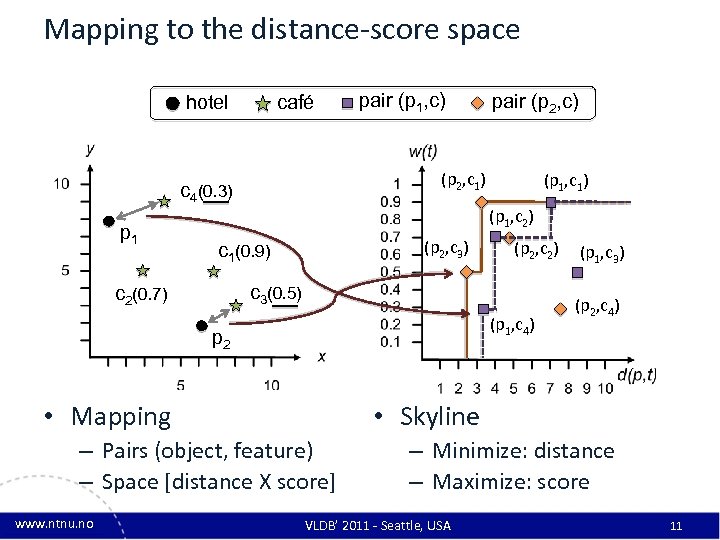Mapping to the distance-score space hotel café (p 1, c 1) (p 1, c 2) (p 2, c 3) c 1(0. 9) (p 2, c 2) c 3(0. 5) c 2(0. 7) (p 1, c 4) p 2 • Mapping (p 1, c 3) (p 2, c 4) • Skyline – Pairs (object, feature) – Space [distance X score] www. ntnu. no pair (p 2, c) (p 2, c 1) c 4(0. 3) p 1 pair (p 1, c) – Minimize: distance – Maximize: score VLDB’ 2011 - Seattle, USA 11

Theoretical properties • SKY(p, Fi) is sufficient to determine the partial score of p for any spatial preference query – Maintaining SKY(p, Fi) is sufficient to answer any spatial preference query (stored in an R-tree) • SKY(p, Fi) is the minimum set required – The data required to process range queries permits processing nn and influence queries • The proofs of theorems can be found in the paper www. ntnu. no VLDB’ 2011 - Seattle, USA 12

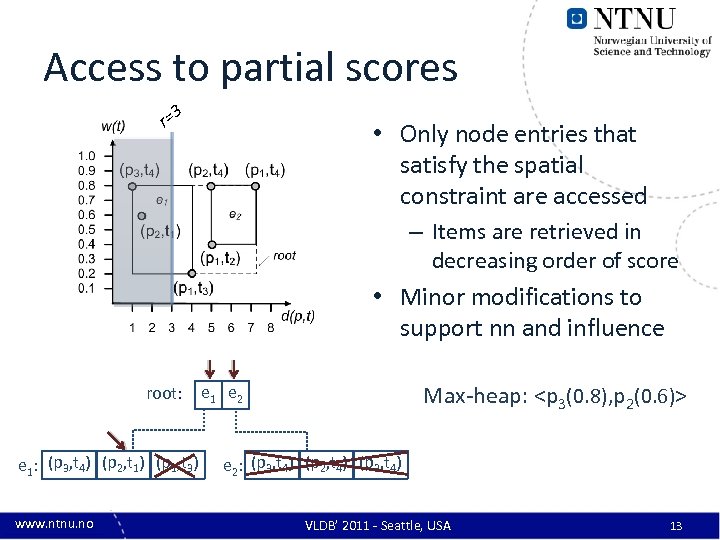Access to partial scores 3 r= • Only node entries that satisfy the spatial constraint are accessed – Items are retrieved in decreasing order of score • Minor modifications to support nn and influence root: e 1: (p 3, t 4) (p 2, t 1) (p 1, t 3) www. ntnu. no Max-heap:

e 1 e 2: (p 3, t 4) (p 2, t 4) (p 3, t 4) VLDB’ 2011 - Seattle, USA 13

Query processing • Compute top-k data objects progressively aggregating partial scores retrieved from Ri – Similar to Fagin’s algorithm (NRA) • Algorithm – Each time an object p is retrieved from Ri, any unseen object p’ in Ri has a score(p’) ≤ score(p) – Keep track of lower and upper-bound score of the seen objects – Terminates when the lower-bound of the k-th object is better than the upper-bound of the remaining objects www. ntnu. no VLDB’ 2011 - Seattle, USA 14

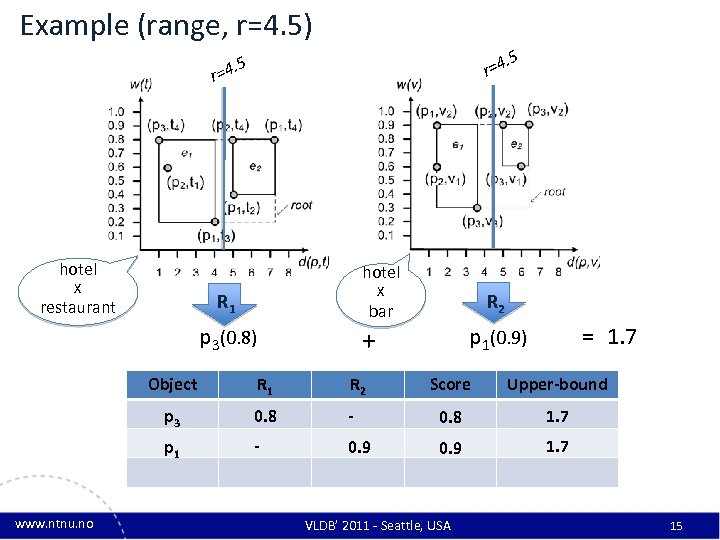Example (range, r=4. 5) 5 . r=4 . 5 r=4 hotel X X R 1 restaurant p 3(0. 8) p 1(0. 9) + Object R 1 R 2 p 3 0. 8 p 1 www. ntnu. no R 2 bar - = 1. 7 Score Upper-bound - 0. 8 1. 7 0. 9 1. 7 VLDB’ 2011 - Seattle, USA 15

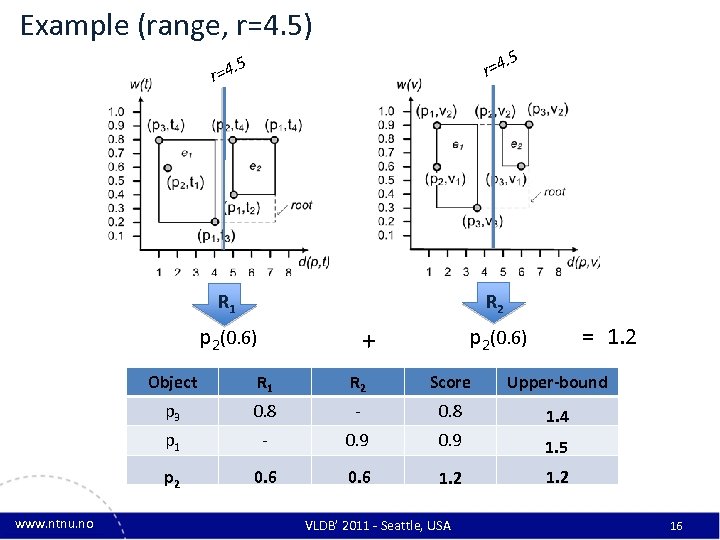Example (range, r=4. 5) 5 . 5 r=4 R 1 R 2 p 2(0. 6) + = 1. 2 Object R 2 Score Upper-bound p 3 0. 8 - 0. 8 1. 4 p 1 - 0. 9 1. 5 p 2 www. ntnu. no R 1 0. 6 1. 2 VLDB’ 2011 - Seattle, USA 16

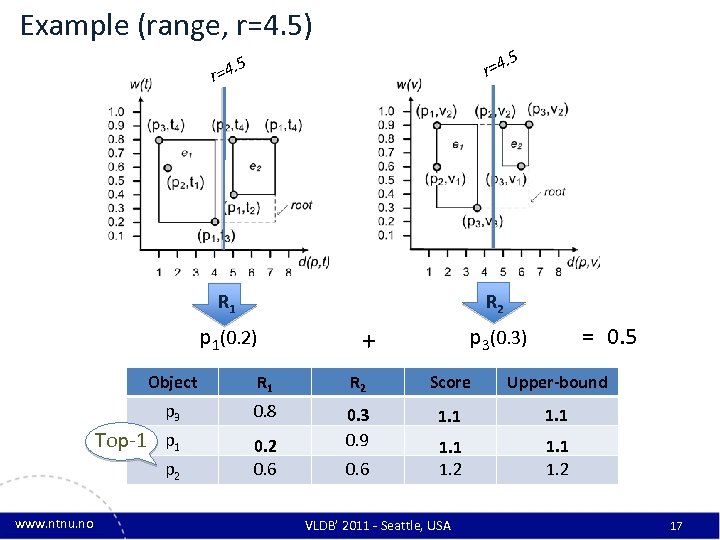Example (range, r=4. 5) 5 . 5 r=4 R 1 R 2 p 1(0. 2) p 3(0. 3) + = 0. 5 Object R 1 R 2 Score Upper-bound p 3 0. 8 1. 1 Top-1 p 1 0. 2 0. 6 0. 3 0. 9 1. 1 1. 2 p 2 www. ntnu. no 0. 6 VLDB’ 2011 - Seattle, USA 17

Materialization • Objects are partitioned into regions – The distance among objects in the same region is small – The skyline set of the objects in the same region is similar with high probability • Compute SKY(R, Fi) for the region R – SKY(p, Fi) SKY(R, Fi), ∀p R • Advantage – The feature set is accessed only once to compute the dynamic skyline of all objects in the region www. ntnu. no VLDB’ 2011 - Seattle, USA 18

Experimental evaluation • We compare our approach (SFA) against SP, GP, BB*, and FJ algorithms [1, 2] • All approaches are implemented in Java • Measures: response time, I/O, update time, index construction time, and index size [1] Yiu, M. L. , Dai, X. , Mamoulis, N. , Vaitis, M. , : “Top-k spatial preference queries”, ICDE, 2007. [2] Yiu, M. L. , Lu, H. , Mamoulis, N. , Vaitis, M. : “Ranking spatial data by quality preferences”, TKDE, 2011. www. ntnu. no VLDB’ 2011 - Seattle, USA 19

Variables studied • Data distribution – Uniform (UN), Synthetic (CN), Real (RL) • Cardinality (object and features) – 50 K, 100 K, 200 K, 400 K, 800 K, 1600 K • Number of results (k) – 10, 20, 30, 40, 50 • Number of feature sets – 1, 2, 3, 4 5 • Query range (r), for range and influence queries – 10, 40, 160, 640, 2560 www. ntnu. no VLDB’ 2011 - Seattle, USA 20

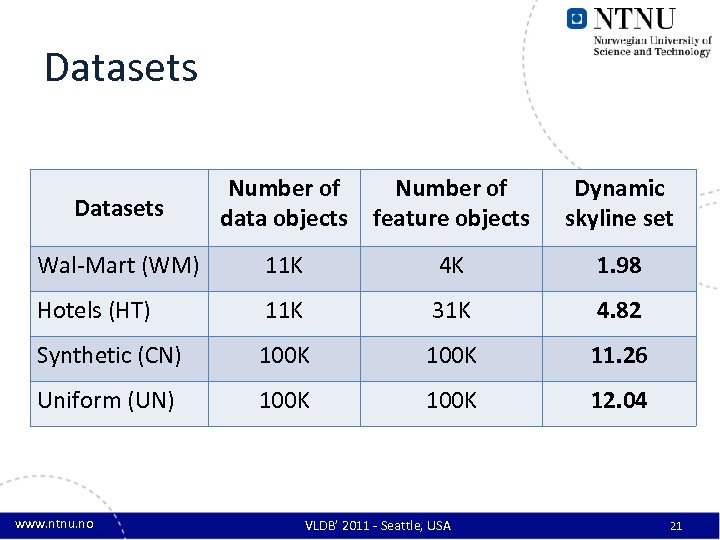Datasets Number of data objects Number of feature objects Dynamic skyline set Wal-Mart (WM) 11 K 4 K 1. 98 Hotels (HT) 11 K 31 K 4. 82 Synthetic (CN) 100 K 11. 26 Uniform (UN) 100 K 12. 04 www. ntnu. no VLDB’ 2011 - Seattle, USA 21

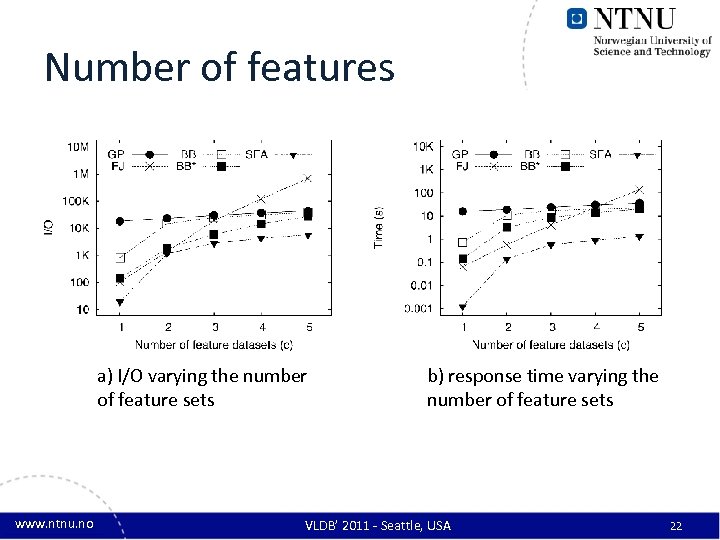Number of features a) I/O varying the number of feature sets www. ntnu. no b) response time varying the number of feature sets VLDB’ 2011 - Seattle, USA 22

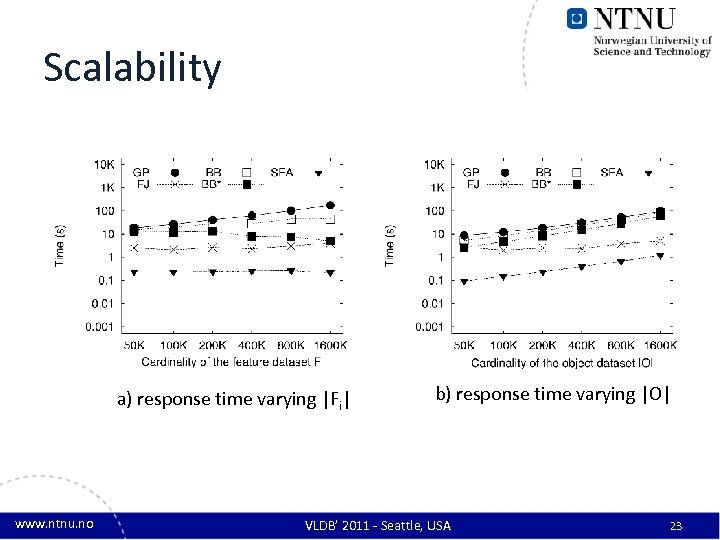Scalability a) response time varying |Fi| www. ntnu. no b) response time varying |O| VLDB’ 2011 - Seattle, USA 23

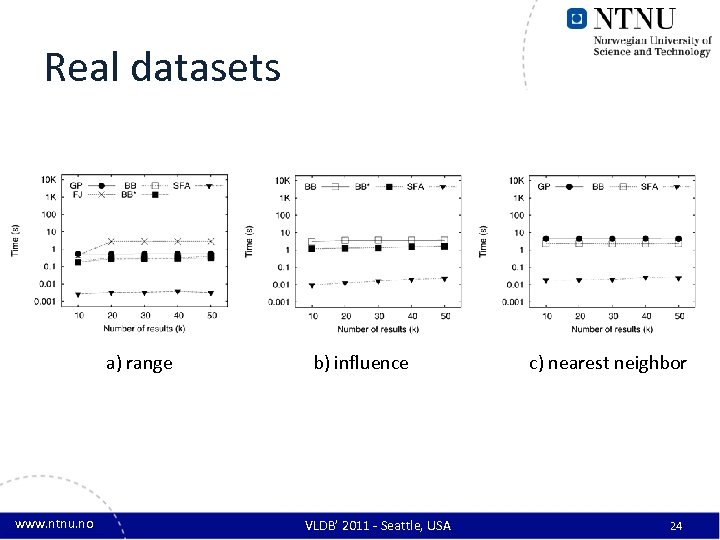Real datasets a) range www. ntnu. no b) influence VLDB’ 2011 - Seattle, USA c) nearest neighbor 24

Conclusion • Top-k spatial preference queries are a useful tool for novel location-based applications • We propose a new approach for processing top-k spatial preference queries efficiently – We find and materialize SKY(p, Fi) – We prove that SKY(p, Fi) is sufficient to determine the partial score of p for any spatial preference query – The size of SKY(p, Fi) is small in practice • We propose algorithms to process queries using our index • The efficiency of our approach is verified through experiments on synthetic and real datasets www. ntnu. no VLDB’ 2011 - Seattle, USA 25

Thanks! More information: João B. Rocha-Junior joao@idi. ntnu. no http: //www. idi. ntnu. no/~joao www. ntnu. no VLDB’ 2011 - Seattle, USA 26