6819a8a5f9bebc3b55dbd8f37c79bbf1.ppt
- Количество слайдов: 38

Effect Of Intrusion Detection on Reliability of Mission-Oriented Mobile Group Systems in Mobile Ad Hoc Networks Author: J. H. Cho, I. R. Chen and P. G. Feng IEEE Transactions on Reliability, Vol. 59, No. 1, 2010, pp. 231 -241. [P 1] (4/6 - Presented by R. Mitchell, C. Jian, and A. H. Saoud)

Outline ü ü • • 2 Introduction (A. H. Saoud) System Model (A. H. Saoud) Performance Model (R. Mitchell) Parameterization (R. Mitchell) Numerical Results, and Analysis (C. Jian) Applicability & Conclusion (C. Jian)

Introduction • Analyzing the effect of intrusion detection system (IDS) techniques on the reliability of a mission-oriented group communication in mobile ad hoc networks. • Knowing design conditions for employing intrusion detection system (IDS) techniques that can enhance the reliability, and thus prolong the lifetime of GCS. • Limitations. • Techniques (prevention, detection, recovery). 3

Introduction • Applying model-based quantitative analysis to security analysis. • MTTSF is a measure to reflect the expected system lifetime, representing a measure against loss of service availability, or system integrity. • Identify the optimal rate at which IDS should be executed to maximize the system lifetime. 4

Introduction • Consider the effect of security threats, and counter IDS techniques on system lifetime of a mission-oriented GCS in MANETs. • Mathematical models to identify the optimal intrusion detection rate at which MTTSF is maximized through analyzing the tradeoff between positive and negative effects of IDS. • Show that the analysis methodology developed is generally applicable to varying network conditions. 5

System Model • The notion of a mobile group is defined based on “connectivity. ” • The GCS, and its constituent mobile groups are “mission-oriented” • Mission execution is an application-level goal built on top of connectivity-oriented group communications. • leave rate, rejoin rate, Mobility rate /( + ) probability node is in any group /( + ) probability node is not in any group 6

System Model - Confidentiality • Shared symmetric (group) key for secure group communications, to encrypt the message sent by a member to others in the group for confidentiality. • Rekeying upon group member join/leave/eviction, or group partition/merge events to preserve secrecy. • Group Diffie-Hellman (GDH), a contributory key agreement protocol, used for group key rekeying for decentralized control, and to eliminate a single point of failure. • Identify optimal intrusion detection intervals to maximize MTTSF, leading to improved service availability. 7

System Model - Authentication • Each member has a private key, and public key, available for authentication. • The public keys of all group members preloaded into every node. • No certificate authority (CA), or key revocation. A node’s public key therefore serves as the identifier of the node 8

System Model - IDS • Host-based IDS, each node performs local detection to determine if a neighboring node has been compromised. • The effectiveness of IDS techniques applied: the false negative probability (P 1), and false positive probability (P 2). • Voting-based IDS: • m nodes each preinstalled with host-based IDS • -ve (a) evicting good nodes by always voting “no” to good nodes (b) keeping bad nodes in the system by al- ways voting “yes” to bad nodes. 9

System Model –IDS Tolerance • False negative probability, and false positive probability. Calculated based on • (a) the per-node false negative, and positive probabilities of host-based IDS in each node; (b) the number of vote-participants selected to vote for or against a target node. (c) an estimate of the current number of compromised nodes • For the selection of participants, each node periodically exchanges its routing information, location, and identifier with its neighboring nodes. 10

System Model – Tolerance 2 • With respect to a target node, all neighbor nodes that are within a number of hops from the target node are candidates as voteparticipants. • A coordinator is selected randomly by introducing a hashing function that takes in the identifier of a node concatenated with the current location of the node as the hash key. • The node with the smallest returned hash value would then become the coordinator 11

System Model – Tolerance 3 • Coordinator selects m nodes randomly and broadcasts the list of m nodes. • Any node not following the protocol raises a flag as a potentially compromised node, and may get itself evicted when it is being evaluated as a target node. • The vote-participants are known to other nodes, and based on votes received, they can determine whether or not a target node is to be evicted. 12

System Model – Failure Def • System Failure Definition 1 (SF 1), which is when the GCS fails when any mobile group fails; • System Failure Definition 2 (SF 2), which is when the GCS fails when all mobile groups fail. • Evaluation of the effect of the two system failure definitions on the MTTSF of the system. 13

System Module – Failure Con. • Condition 1 (C 1): undetected member requests and obtains data using the group key. (leading to the loss of system integrity • Condition 2 (C 2): more than 1/3 of group member nodes are compromised, but undetected by IDS. This failure condition follows the Byzantine Failure model (loss of availability of system service). 14

System Model - Connectivity • Single hop, single group, not experiencing group merge or partition events. • SF 1 and SF 2 are the same. • Multi-hops so that there are multiple groups in the system due to group partition/merge. 15

System Module – Reliability • MTTSF: indicates the lifetime of the GCS before it fails. • A GCS fails when one mobile group fails, or when all mobile groups fail in the missionoriented GCS, as defined by SF 1 or SF 2. • a mobile group fails when either C 1 or C 2 is true. • A lower MTTSF implies a faster loss of system integrity, or availability. 16

Outline • • ü ü • • 17 Introduction (A. H. Saoud) System Model (A. H. Saoud) Performance Model (R. Mitchell) Parameterization (R. Mitchell) Numerical Results, and Analysis (C. Jian) Applicability & Conclusion (C. Jian)

Performance Model • • 18 SPN Places Transitions Review
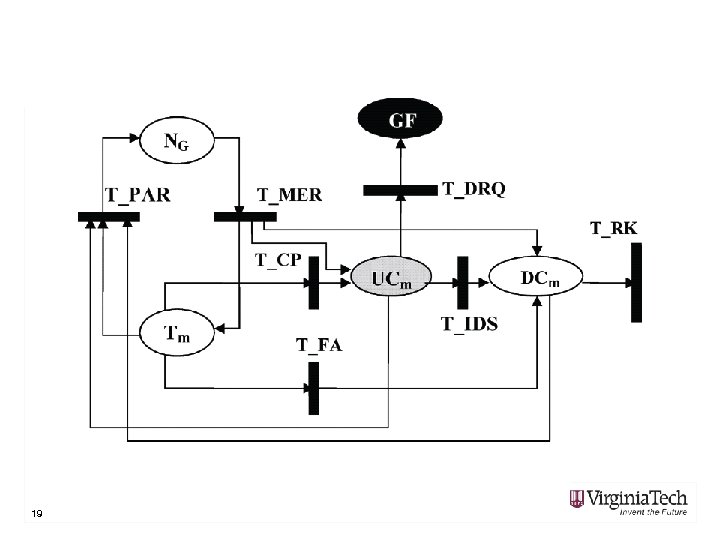
19

Places • • groups NG uncompromised members Tm undetected compromised nodes UCm evicted nodes DCm • well detected compromised • false detected uncompromised • security failure GF • absorbing 20

Transitions • • • group partition TPAR group merge TMER member compromise TCP false detection TFA confidentiality violation (C 1) TDRQ • rate = λq · mark(UCm) · p 1 • well detection TIDS • rekey TRK 21

Review • Why is TDRQ rate scaled by p 1? • Where is the Byzantine failure (C 2) transition into GF? • TBYZ from UCm with multiplicity mark(Tm) / 2 • Derive SF 2 reward model 22

Parameterization • • 23 TRK rate TCP rate IDS interval δ Pfp and Pfn

TRK rate • For one group: • b. GDH / datalink rate • For multiple groups: • 3 b. GDH(N-1) / datalink rate 24

TCP rate • adversary becomes more aggressive when they have the upper hand • λc · (mark(Tm) + mark(UCm) / mark(Tm)) 25

IDS interval δ • IDS becomes more aggressive as it detects more compromised nodes • (TIDS)-1 · (Ninit / (mark(Tm) + mark(Ucm)) 26
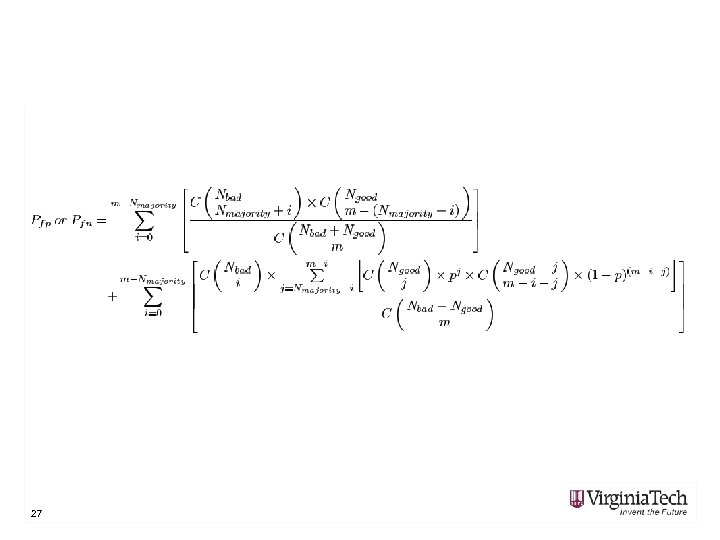
27

Outline • • ü ü 28 Introduction (A. H. Saoud) System Model (A. H. Saoud) Performance Model (R. Mitchell) Parameterization (R. Mitchell) Numerical Results, and Analysis (C. Jian) Applicability & Conclusion (C. Jian)
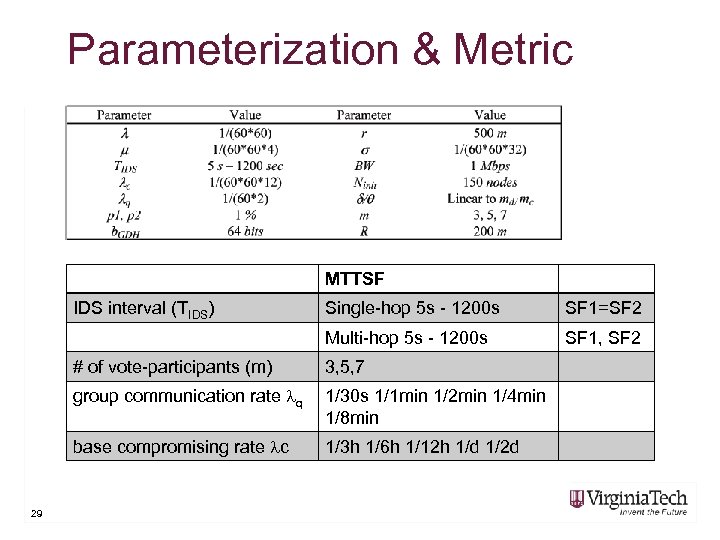
Parameterization & Metric MTTSF IDS interval (TIDS) Single-hop 5 s - 1200 s SF 1=SF 2 Multi-hop 5 s - 1200 s SF 1, SF 2 # of vote-participants (m) group communication rate q 1/30 s 1/1 min 1/2 min 1/4 min 1/8 min base compromising rate c 29 3, 5, 7 1/3 h 1/6 h 1/12 h 1/d 1/2 d
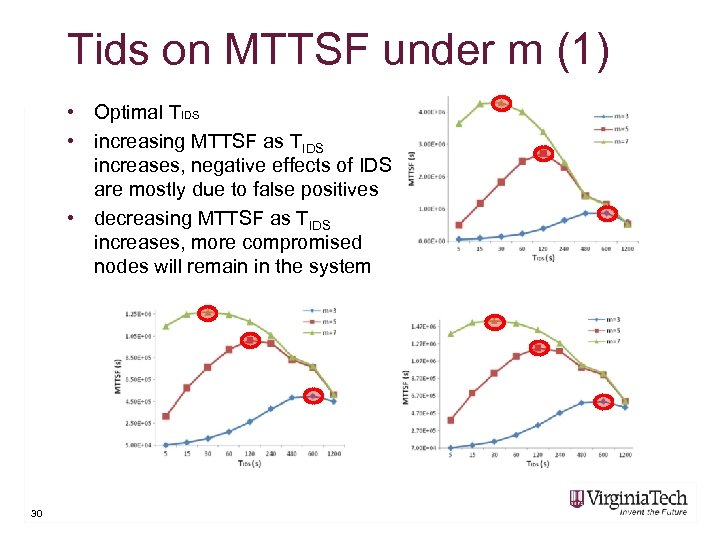
Tids on MTTSF under m (1) • Optimal TIDS • increasing MTTSF as TIDS increases, negative effects of IDS are mostly due to false positives • decreasing MTTSF as TIDS increases, more compromised nodes will remain in the system 30
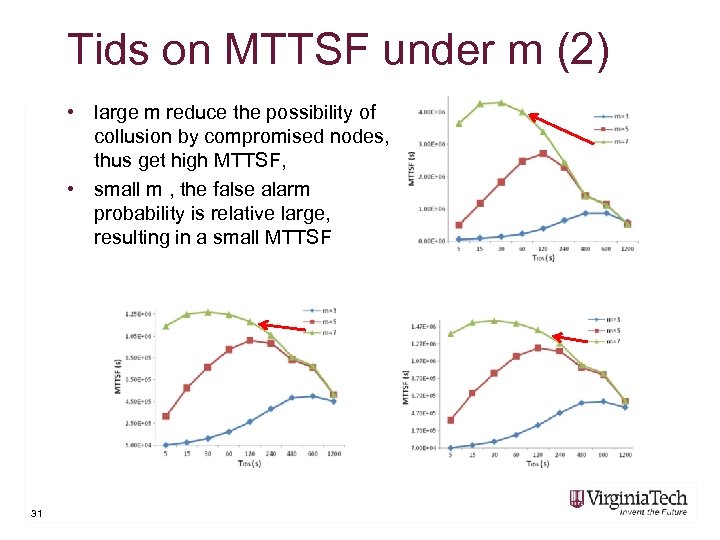
Tids on MTTSF under m (2) • large m reduce the possibility of collusion by compromised nodes, thus get high MTTSF, • small m , the false alarm probability is relative large, resulting in a small MTTSF 31
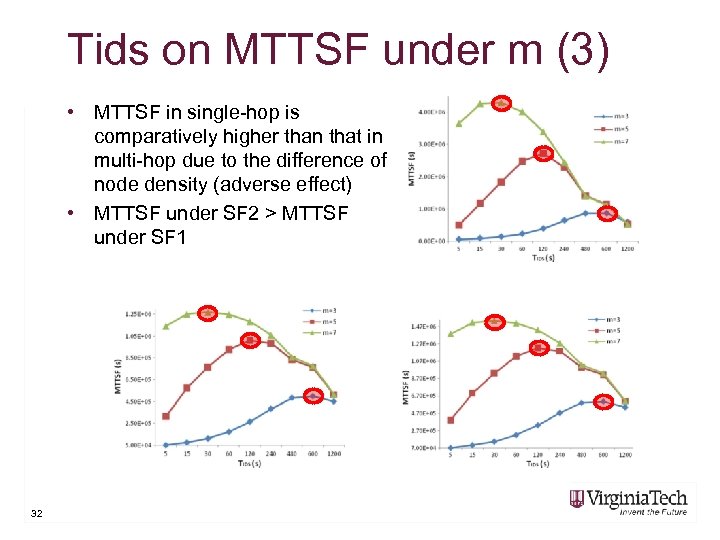
Tids on MTTSF under m (3) • MTTSF in single-hop is comparatively higher than that in multi-hop due to the difference of node density (adverse effect) • MTTSF under SF 2 > MTTSF under SF 1 32
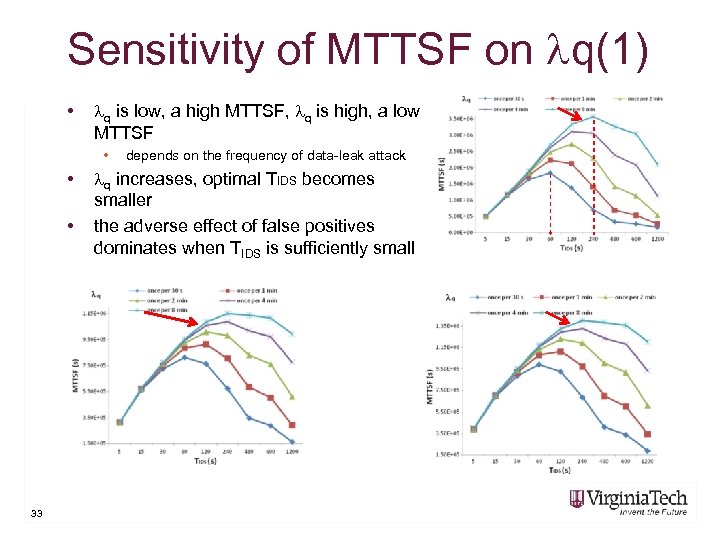
Sensitivity of MTTSF on q(1) • q is low, a high MTTSF, q is high, a low MTTSF • • • 33 depends on the frequency of data-leak attack q increases, optimal TIDS becomes smaller the adverse effect of false positives dominates when TIDS is sufficiently small
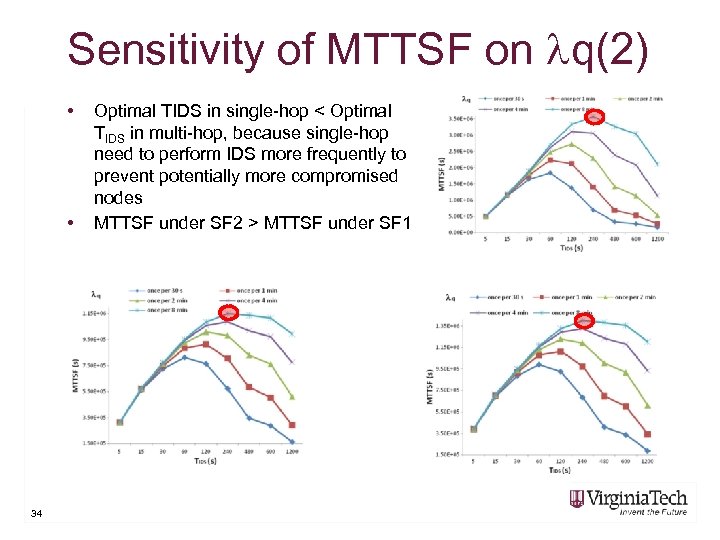
Sensitivity of MTTSF on q(2) • • 34 Optimal TIDS in single-hop < Optimal TIDS in multi-hop, because single-hop need to perform IDS more frequently to prevent potentially more compromised nodes MTTSF under SF 2 > MTTSF under SF 1
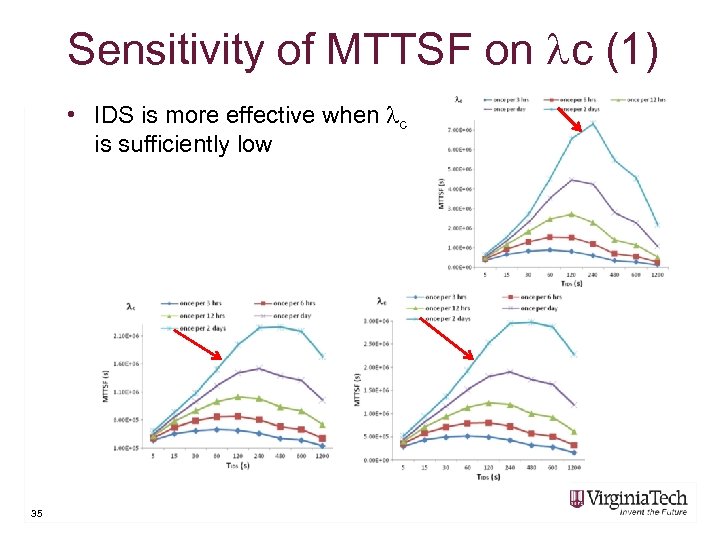
Sensitivity of MTTSF on c (1) • IDS is more effective when c is sufficiently low 35
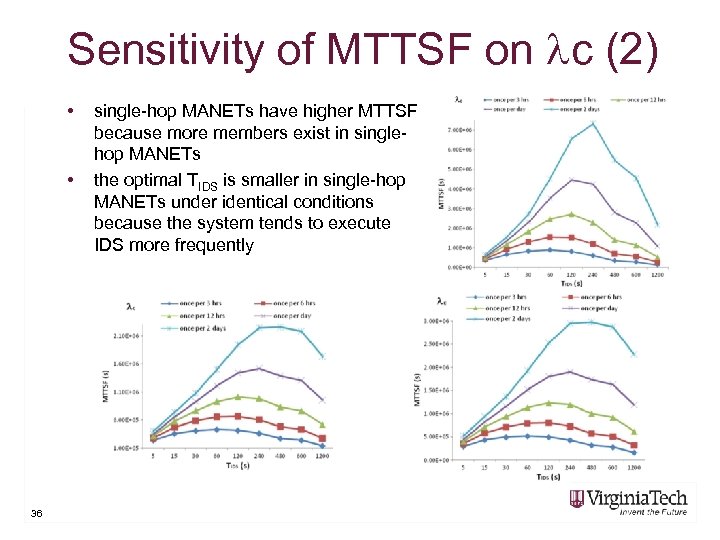
Sensitivity of MTTSF on c (2) • • 36 single-hop MANETs have higher MTTSF because more members exist in singlehop MANETs the optimal TIDS is smaller in single-hop MANETs under identical conditions because the system tends to execute IDS more frequently

Conclusion • a mathematic model • input: operational conditions, system failure definitions, attacker behaviors • output: the optimal rate to execute intrusion detection to enhance the system reliability of GCS • results • TIDS , as m , node density or group size , q c 37

Questions?
6819a8a5f9bebc3b55dbd8f37c79bbf1.ppt