EE 369 Discrete Math Propositional Logic Guest Lecturer

EE 369: Discrete Math Propositional Logic Guest Lecturer: Paul Wood (pwood@purdue. edu and on Piazza) Spring 2018 – EE 369 Prof. Saurabh Bagchi T/R 10: 30 -11: 45 am -- ME 1061 1

Outline • Logic • Propositional Logic • Well formed formula • Truth table • Tautology & Contradiction • Proof System for Propositional Logic • Deduction method • Formalizing English arguments • Text book chapters 1. 1 and 1. 2 2

Logics To define a logic, answer three questions: 1. What are the models? 2. What are the formulas? 3. Which formulas are true in which models? A logic is a formal system relating syntax (formulas) and semantics (models of the world). 3

Propositional Logic: Models • A statement or a proposition is a sentence that is either true or false. Represented as upper cap letters of the alphabet. – “She is very talented” – “There are life forms on other planets in the universe” – Q: “Today is Tuesday” • Statement letters can be combined into new statements using logical connectives of – – – conjunction (AND, ) disjunction (OR, ) implication ( ) equivalence ( ) negation ( or ) 4

Propositional Logic: Formulas • Truth tables define how each of the connectives operate on truth values. • Truth table for implication ( ) • Equivalence connective A B is shorthand for (A B) (B A) • Truth table for equivalence ( ) • Binary & unary connective 5

When is a formula true in a model? • Each Boolean connective has a truth table e. g. P T T F F Q T F P Q T T T F P T T F F Q T F P Q T F F F P F T 6

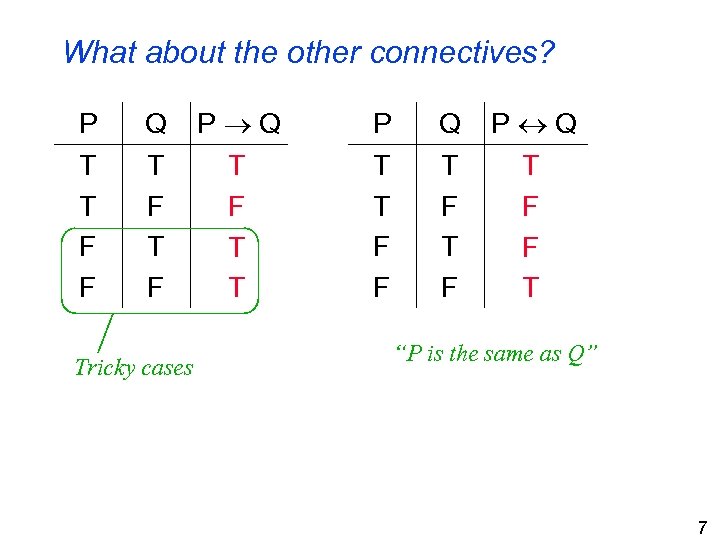What about the other connectives? P T T F F Q T F Tricky cases P Q T F T T P T T F F Q T F P Q T F F T “P is the same as Q” 7

Abstract: What about new connectives? ☺ P T T F F Q T F P☺Q T T F T Truth tables define the connective 8

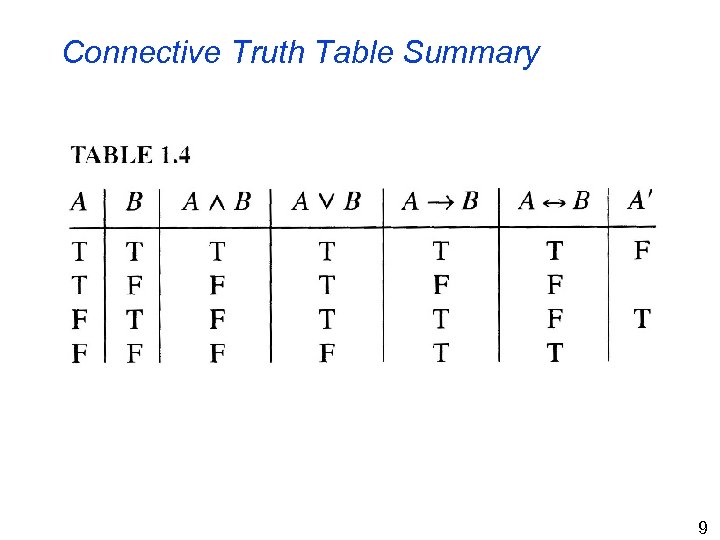Connective Truth Table Summary 9

Connectives in English 10

Clarifications from 1/8/17 Flowers will bloom only if it rains A can be true only if B is also true If flowers bloom then it rains 11

Example formulas and non-formulas • “If the rain continues, then the river will flood. ” Express by implication. • A: the rain continues B: the river floods • If A, then B: ---- A B • If the river floods, did the rain continue? A B T T T F F T 12

Example formulas and non-formulas • “A good diet is a necessary condition for a healthy cat. ” Express by implication. • C: the cat has a good diet D: the cat is healthy “B is a necessary condition for A”: A B Thus D C 13

Example formulas and non-formulas • “Julie likes butter but hates cream. ” Negate this. • A: Julie likes butter B: Julie hates cream “A but B” ---- A B Need (A B)’ 14

Example formulas and non-formulas • “Julie likes butter but hates cream. ” Negate this. • Negation: A T T F F B A B (A B)’ T T F F F T T F F T A’ B’ F F F T T A’ B’ F T T T 15

Example formulas and non-formulas • “Julie likes butter but hates cream. ” Negate this. A T T F F B A B (A B)’ T T F F F T T F F T A’ B’ F F F T T A’ B’ F T T T • A’: Julie does not like butter B’: Julie does not hate (likes) cream Julie does not like butter or likes cream 16

Additional Negation Examples 1. The processor is fast but the printer is slow • Either the processor is slow or the printer is fast 2. The processor is fast or else the printer is slow • The processor is slow and the printer is fast 3. If the processor is fast then the printer is slow • The processor is fast but so is the printer 17

Additional Statement Examples • Which are statements: A. B. C. D. E. F. G. The moon is made of green cheese. He is certainly a tall man. Two is a prime number. Will the game be over soon? Next year interest rates will rise. Next year interest rates will fall. X^2 – 4 = 0 18

Additional Logic Examples • What is the truth value of each statement: A. 8 is even or 6 is odd B. 8 is even and 6 is odd C. 8 is odd or 6 is odd D. 8 is odd and 6 is odd E. If 8 is odd, then 6 is odd F. If 8 is even, then 6 is odd G. If 8 is odd, then 6 is even 19

Additional Negation Examples • Which statements are correct negations? – The answer is either 2 or 3. 1. Neither 2 nor 3 is the answer. 2. The answer is not 2 or not 3. 3. The answer is not 2 and it is not 3. – Cucumbers are green and seedy. 1. Cucumbers are not green and not seedy. 2. Cucumbers are not green or not seedy. 3. Cucumbers are green and not seedy. 20

Additional Negation Examples (Continued) – Flowers will bloom only if it rains 1. The flowers will bloom but it will not rain 2. The flowers will not bloom and it will not rain 3. The flowers will not bloom or else it will not rain – If you build it, they will come. 1. If you build it, then they won’t come. 2. You don’t build it, but they do come 3. You build it, but they don’t come. 21

Formulas & Precedence • Well-formed formula: A valid string with statement letters, connectives, and parentheses – (((A B))) D – (A B) (C A) • Non-WFF – (A B))) (C A) 22

Formulas & Precedence • Precedence – A B C (A B) C OR A (B C)? • Rules: 1. 2. 3. 4. 5. Innermost parenthesis () first Negation ‘ , 23

Formulas & Precedence • Main connective: Last connective to be applied in a WFF – (A B) (C A) – (A B) C – (((A B) (C )) A) 24

Example of Truth Table for a WFF • Compound WFF (A B) (C A) For Reference: P T T F F Q T F P Q T F T T • # rows in a truth table with n statement letters = ? 25

Truth Table Scale 26

Tautologies and Contradictions • A tautology is a formula that is true in every model. (also called a theorem) – for example, (A A) is a tautology – What about (A B) (A B )? – Look at tautological equivalences on pg. 8 of text • A contradiction is a formula that is false in every model. – for example, (A A) is a contradiction 27

Some Tautological Equivalences 28

De Morgan’s Laws • (A B) = A B • Negate “The couch is either new or comfortable. ” • (A B) = A B • Negate “The book is thick and boring. ” 29

De Morgan’s by Truth Table • (A B) = A B A T T F F B A B (A B)’ T T F F F T T F F T A’ B’ F F F T T A’ B’ F T T T 30

English Translation Examples • Let A, B, C be: – A Roses are red – B Violets are blue – C Sugar is sweet a)Roses are red and violets are blue b)Roses are red, and either violets are blue or sugar is sweet c)Whenever violets are blue, roses are red and sugar is sweet 31

English Translation Examples • Let A, B, C be: – A Roses are red – B Violets are blue – C Sugar is sweet a)Roses are red only if violets aren’t blue or sugar is sour. b)Roses are red and, if sugar is sour, then either violets aren’t blue or sugar is sweet. 32

English Translation Examples • Let A, B, C be: – A Roses are red – B Violets are blue – C Sugar is sweet • Translate to English: a) B C b) B (A C) c) (C A ) B 33

English Translation Examples 1. A sufficient condition for the knight to win is that the armor is strong or the horse is fresh. 2. The knight will win only if the horse is fresh and the armor is strong. 3. The economy will remain strong if and only if Anita wins the election or tax rates are reduced. 34

WFF Truth Table • Construct the truth table for: 35

1. 1 Objectives and Summary • You can now: – Construct truth tables from WFF’s – Define tautologies and contradictions • Summary: – WFFs are symbolic representations of statements • “Julie likes milk but not cream. ” : A B – Truth values for compound WFF’s depend on inputs and connectives • # of rows = 2^n 36

Utility of Proofs and English Translations • Program verification (Chapter 1. 6) – A formal proof can verify program behavior • Customer specification translations – System specifications: • If a customer visits the website, she can add the product to the cart. If she adds the product to the cart, then she can checkout. If she checks out, then she can purchase the product. She visits the website. Therefore, she can purchase the product. 37

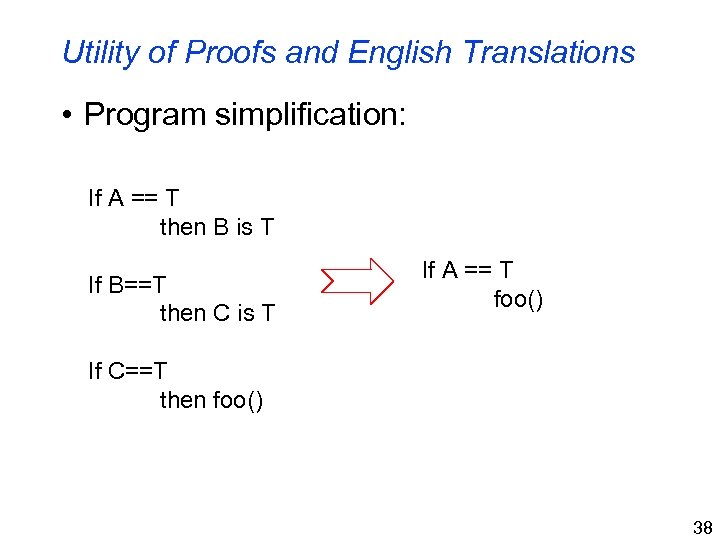Utility of Proofs and English Translations • Program simplification: If A == T then B is T If B==T then C is T If A == T foo() If C==T then foo() 38

A Proof System • A proof system is a syntactic system for finding formulas implied by the hypotheses – “syntactic” means manipulating syntax • i. e. manipulating formulas rather than models. – P 1 P 2 … Pn Q is a tautology (true in every model) • A proof is a sequence of formulas, where each formulas in the sequence is either – a hypothesis – a formula justified by previous formulas and a proof rule • The sequence “proves” the last formula 39

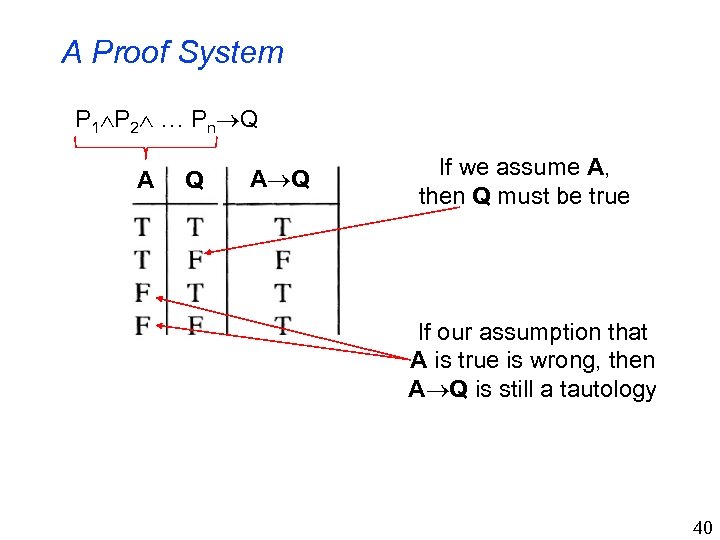A Proof System P 1 P 2 … Pn Q A Q If we assume A, then Q must be true If our assumption that A is true is wrong, then A Q is still a tautology 40

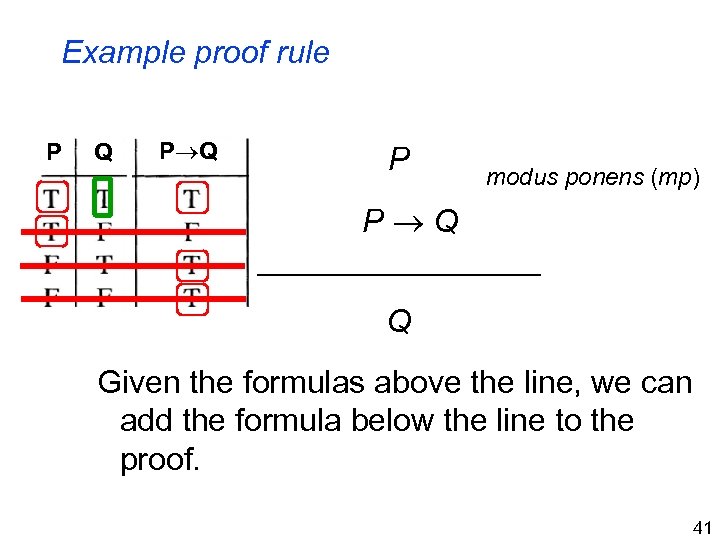Example proof rule P Q P modus ponens (mp) P Q ________ Q Given the formulas above the line, we can add the formula below the line to the proof. 41

Example proof • Hypotheses: C, B, B (C A) • Conclusion: A 1. 2. 3. 4. 5. B B (C A) C A premise 1, 2, mp premise 3, 4, mp 42

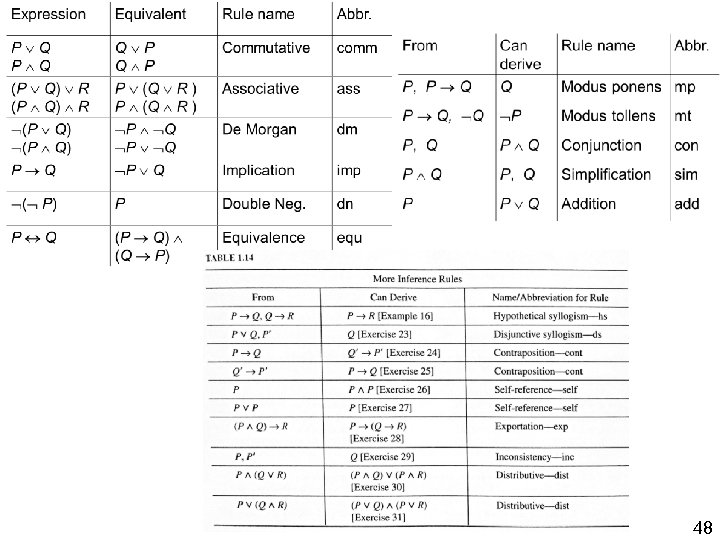
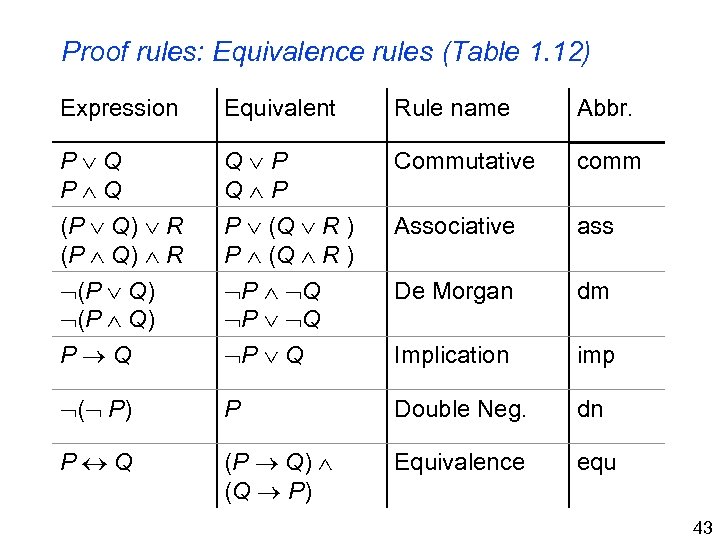Proof rules: Equivalence rules (Table 1. 12) Expression Equivalent Rule name Abbr. P Q Q P Commutative comm (P Q) R P (Q R ) Associative ass (P Q) P Q De Morgan dm P Q P Q Implication imp ( P) P Double Neg. dn P Q (P Q) (Q P) Equivalence equ 43

Example Equivalence 44

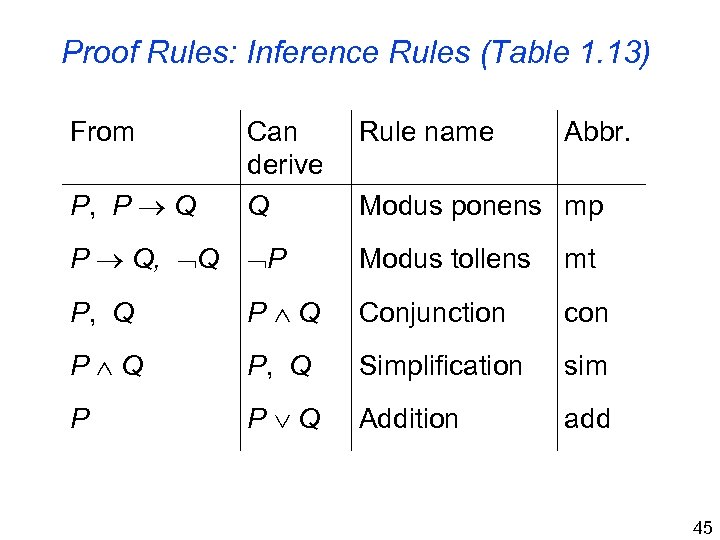Proof Rules: Inference Rules (Table 1. 13) From Rule name P, P Q Can derive Q Abbr. P Q, Q P Modus tollens mt P, Q P Q Conjunction con P Q P, Q Simplification sim P P Q Addition add Modus ponens mp 45

Example: Logical Inferences What can be concluded? 1. If the car was involved in the hit-and-run, then the paint would be chipped. But the paint is not chipped. 2. If the bill was sent today, then you will be paid tomorrow. You will be paid tomorrow. 3. The grass needs mowing and the trees need trimming. If the grass needs mowing, then we need to rake the leaves. 46

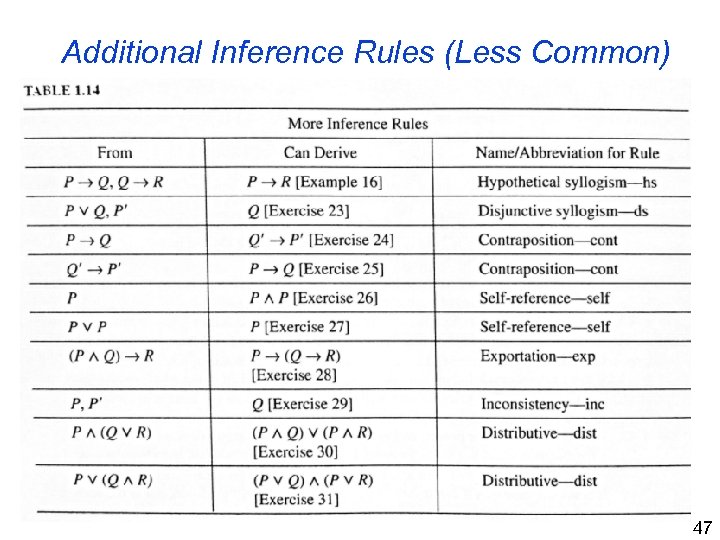Additional Inference Rules (Less Common) 47

48

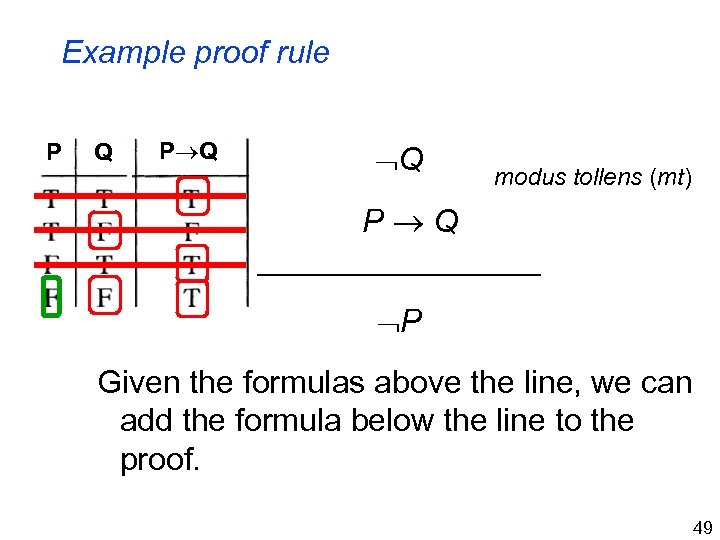Example proof rule P Q Q modus tollens (mt) P Q ________ P Given the formulas above the line, we can add the formula below the line to the proof. 49

Formal Proof • If Bob is hungry, then he will eat. Bob is hungry. Therefore, he will eat. – (H E) H E 1. (H E) hypothesis 2. H hypothesis 3. E 1, 2, modus ponens 50

Further Understanding: Proof Tautology (H E) H E Construct a truth table: Valid Assumption/ Hypothesis B A B H E (H E) H E T T T T F A H E F F F T T F F T Tautology P 1 P 2 … Pn Q is a tautology 51

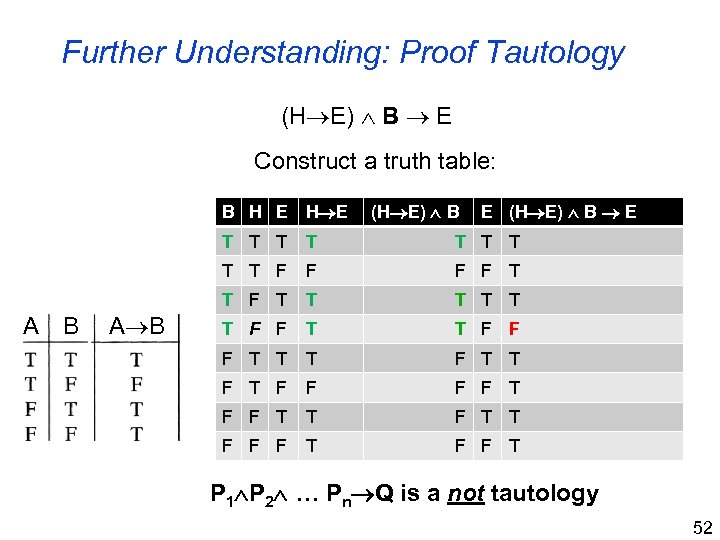Further Understanding: Proof Tautology (H E) B E Construct a truth table: (H E) B E (H E) B E B H E T T T A B T T T F F F T T F T B T T T F A H E T T T F F F T T T F T F F T T F F F T P 1 P 2 … Pn Q is a not tautology 52

Deduction Method in Proofs • When proving P Q… – add P to premises and prove Q. • Repeat to prove P (Q R) – add P and Q to premises and prove R. • To prove: P 1 P 2 … Pn (R S), prove: P 1 P 2 … Pn R S • Rationale: A (B C) A B C is a tautology 53

Equivalence Example • Show: A (B C) A B C 1. A (B C) A (B’ C) (imp) 2. A (B’ C) A’ (B’ C) (imp) 3. A’ (B’ C) (A’ B’) C (ass) 4. (A’ B’) C (A B)’ C (dm) 5. (A B)’ C A B C (imp) 54

Deduction Example 1 (P Q) (P’ Q’) = (P Q) P’ Q’ 1. P Q 2. P’ 3. Q’ hyp 1, 2, mt 55

Deduction Example 2 (Q’ P’) (P Q) = (Q’ P’) P Q 1. 2. 3. 4. 5. Q’ P’ P (P’)’ (Q’)’ Q’ hyp 2, dn 1, 3, mt 4, dn 56

Proof System vs. Truth Tables P P’ Q (False) Q A B 1. 2. 3. 4. 5. 6. 7. 8. P P’ P Q Q P (Q’)’ P Q’ P (Q’)’ Q hyp 1, add 3, comm 4, dn 5, imp 2, 6, mt 7, dn 57

Derivation Hints 1. Use modus ponens (mp) often 2. (A B)’ and (A B)’ are seldom useful; apply (dm) often 3. Wffs A B seldom useful because they do not imply A or B; try using double negation to convert to (A’)’ B then A’ B 4. Try to prove single variables are true first before more complex formulas 58

Other Tricks • Conclusion rewriting – Sometimes the conclusion can be manipulated to reach a better form – Only use equivalence rules … [P’ Q] … [P Q] by implication 59

An Example Proof: Find Justifications (1) Hyp Hyp-deduction 2, 3, mp 1, 4, conjunction 60

An Example Proof: Find Justifications (2) Hyp Hyp 2, 3, con 4, dm 1, 5, mt 61

An Example Proof [(A B ) C] (C D) A D 1. (A B ) C Hyp 2. C D Hyp 3. A Hyp 4. A B 3, add 5. C 1, 4, mp 6. D 2, 5, mp 62

Deduction Example • To prove: P 1 P 2 … Pn (R S), prove: P 1 P 2 … Pn R S • [A (B C)] (A D’) B (D C) 1. A (B C) Hyp/premise 2. A D’ Hyp/premise 3. B Hyp/premise 4. D Hyp/premise (Deduction) 5. D’ A 2, comm 6. D A 5, imp 7. A 4, 6, mp 8. B C 1, 7, mp 9. C 3, 8, mp 63

Prop. Logic Proof: Example 1 64

Prop. Logic Proof: Example 2 65

Prop. Logic Proof: Example 3 66

Prop. Logic Proof: Example 4 67

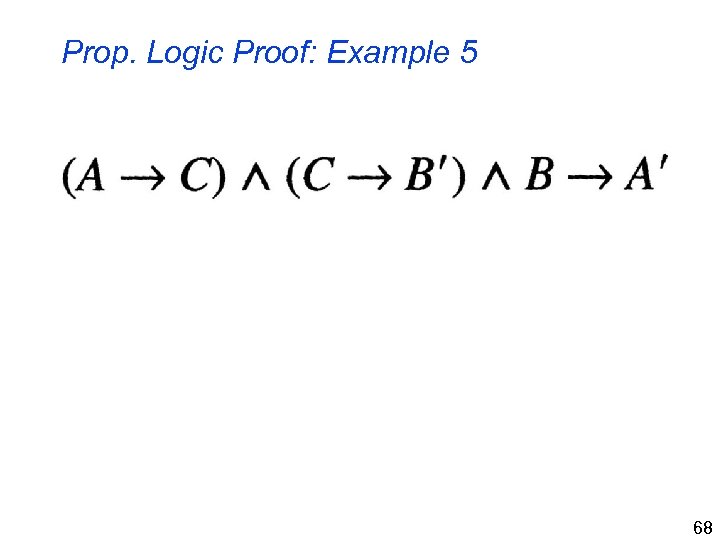Prop. Logic Proof: Example 5 68

Prop. Logic Proof: Example 6 P (Q R) (P Q) (P R) 69

Formalizing English Arguments To formalize an English argument: 1. Find the minimal statements in the argument and symbolize them with propositional letters A, B, … 2. Convert English connectives to propositional ones. 3. Give a proof of the conclusion using the premises. 70

Examples Jack went to fetch a pail of water. Jack fetches a pail of water only if Jack works hard only when Jack is paid. Therefore Jack was paid. 71

Minimal True/False Statements Jack went to fetch a pail of water. Jack fetches a pail of water only if Jack works hard only if Jack is paid. Therefore Jack was paid. A = Jack fetches a pail of water B = Jack works hard C = Jack is paid A. A only if B. B only if C. Therefore C. 72

Eliminating connectives A. A only if B. B only if C. Therefore C. becomes Hypotheses: A, A B, B C. Conclusion: C. Easy to prove that these hypotheses give this conclusion using rule mp. 73

Examples — a bad argument Jack went to fetch a pail of water. Jack fetches a pail of water if Jack works hard if Jack is paid. Therefore Jack was paid. Hypotheses: A, B A, C B. Conclusion: C. Hypotheses do not entail conclusion…to show this, give a model that makes the conclusion false. – A=T, B=T, C=F 74

Another example Fish can walk only if elephants can fly. Elephants can fly only if eggplants can talk. Therefore, eggplants can talk. Is this a valid argument? 75

Another example Fish can walk only if elephants can fly. Elephants can fly only if eggplants can talk. Therefore, eggplants can talk. A: Fish can walk B: Elephants can fly C: Eggplants can talk 76

Another example A. A only if B. B only if C. Therefore, C. A: Fish can walk B: Elephants can fly C: Eggplants can talk Hypothesis: A, A B, B C Conclusion: C 77

Formalizing: Example 1 • If chicken is on the menu, then don’t order fish, but you should have either fish or salad. So if chicken is on the menu, have salad. 78

Formalizing: Example 2 • The crop is good, but there is not enough water. If there is a lot of rain or not a lot of sun, then there is enough water. Therefore the crop is good and there is a lot of sun. 79

Formalizing w/ Proof: Example 1 • If the program is efficient, then it executes quickly. Either the program is efficient, or it has a bug. However, the program does not execute quickly. Therefore it has a bug. 80

Formalizing w/ Proof: Example 2 • If Jane is more popular, then she will be elected. If Jane is more popular, then Craig will resign. Therefore if Jane is more popular, she will be elected and Craig will resign. 81

Formalizing w/ Proof: Example 3 • It is not the case that if electric rates go up, then usage will go down, nor is it true that either new power plants will be built or bills will not be late. Therefore usage will not go down and bills will be late. 82

Examples where propositional logic fails Every positive number is greater than zero. Five is a positive number. Therefore, five is greater than zero. Minimal statements? A = Every positive number is greater than zero. B = Five is a positive number. C = Five is greater than zero. Hypotheses: A, B. Conclusion: C. Conclusion not entailed (consider A = B = T, C = F) Our logic does not model the internal structure of the propositions 83