64ef2b65dca43cf68019b8faa3a2340e.ppt
- Количество слайдов: 38

EE 2174: Digital Logic and Lab Professor Shiyan Hu Department of Electrical and Computer Engineering Michigan Technological University CHAPTER 4 Technology Mapping

Overview More Logic Gates n NAND and NOR circuits n Two-level Implementations n Multilevel Implementations n n Exclusive-OR (XOR) Gates Odd Function n Parity Generation and Checking n 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 2

More Logic Gates n n We can construct any combinational circuit with AND, OR, and NOT gates Additional logic gates are used for practical reasons 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 3
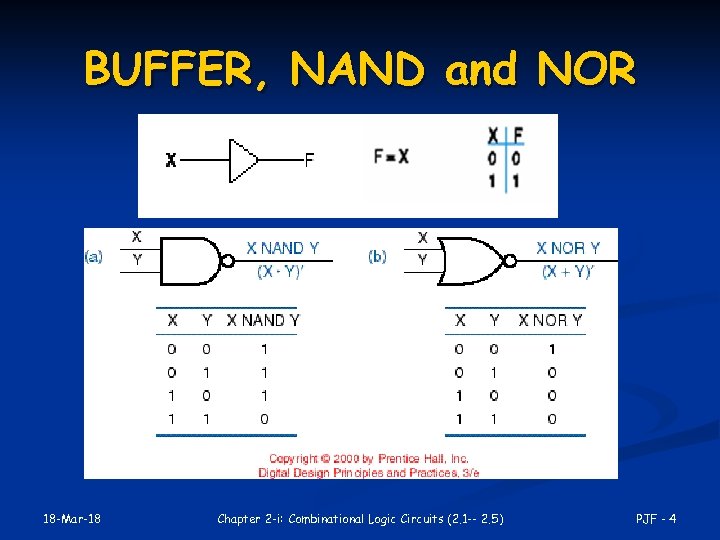
BUFFER, NAND and NOR 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 4
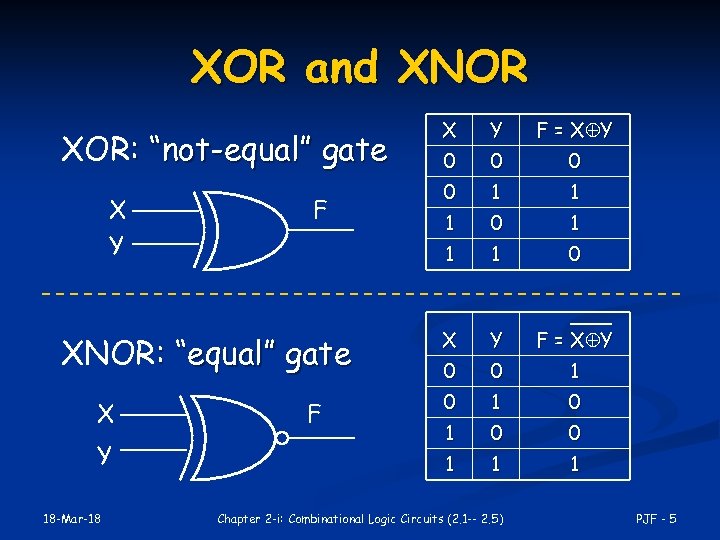
XOR and XNOR X Y XNOR: “equal” gate X Y 18 -Mar-18 F F = X Y 0 0 1 1 1 0 X Y F = X Y 0 0 1 0 1 0 0 1 F Y 1 XOR: “not-equal” gate X 1 1 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 5

NAND Gate Known as a “universal” gate because ANY digital circuit can be implemented with NAND gates alone. n To prove the above, it suffices to show that AND, OR, and NOT can be implemented using NAND gates only. n 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 6
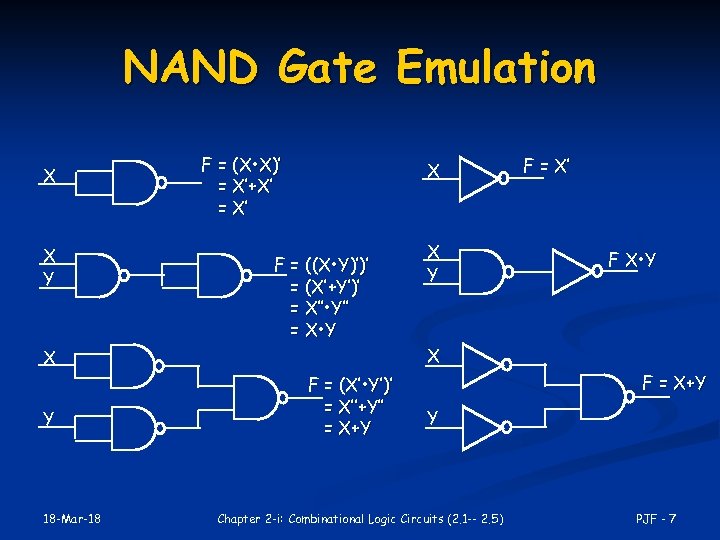
NAND Gate Emulation X X Y F = (X • X)’ = X’+X’ = X’ X F = ((X • Y)’)’ = (X’+Y’)’ = X’’ • Y’’ = X • Y 18 -Mar-18 F X • Y X X Y F = X’ F = (X’ • Y’)’ = X’’+Y’’ = X+Y F = X+Y Y Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 7

NAND Circuits n To easily derive a NAND implementation of a boolean function: n n Find a simplified SOP is an AND-OR circuit Change AND-OR circuit to a NAND circuit Use the alternative symbols below 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 8
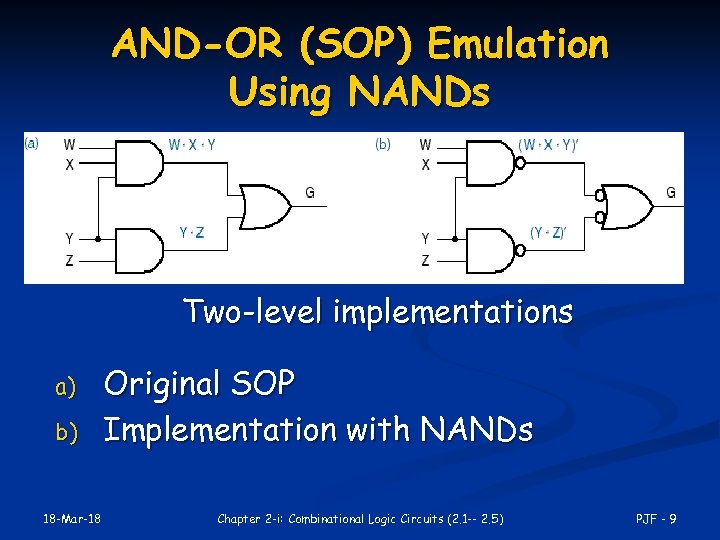
AND-OR (SOP) Emulation Using NANDs Two-level implementations a) b) 18 -Mar-18 Original SOP Implementation with NANDs Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 9
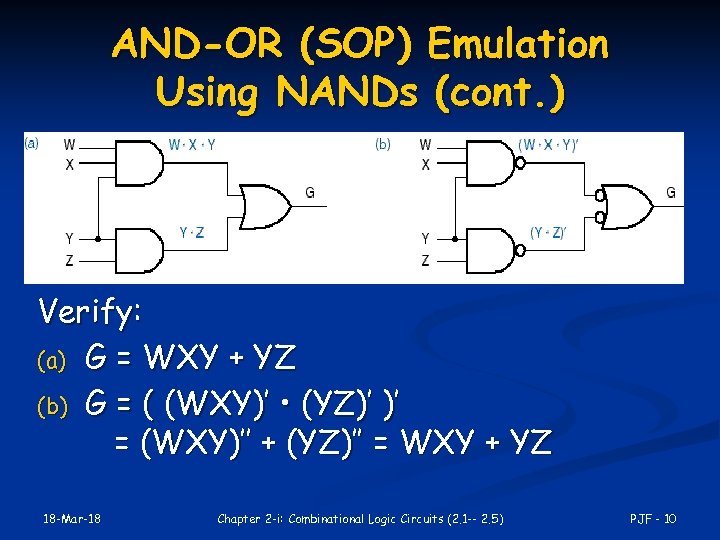
AND-OR (SOP) Emulation Using NANDs (cont. ) Verify: (a) G = WXY + YZ (b) G = ( (WXY)’ • (YZ)’ )’ = (WXY)’’ + (YZ)’’ = WXY + YZ 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 10
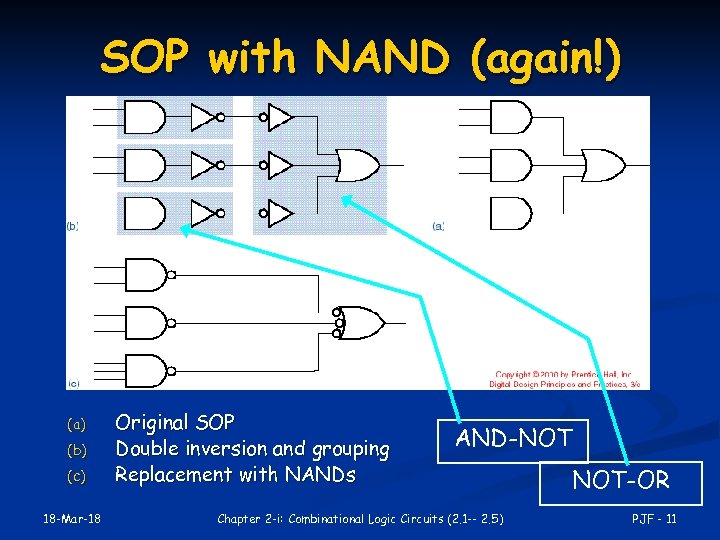
SOP with NAND (again!) (a) (b) (c) 18 -Mar-18 Original SOP Double inversion and grouping Replacement with NANDs AND-NOT Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) NOT-OR PJF - 11

Two-Level NAND Gate Implementation - Example F (X, Y, Z) = m(0, 6) 1. Express F in SOP form: F = X’Y’Z’ + XYZ’ 2. Obtain the AND-OR implementation for F. 3. Add bubbles and inverters to transform AND-OR to NAND-NAND gates. 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 12
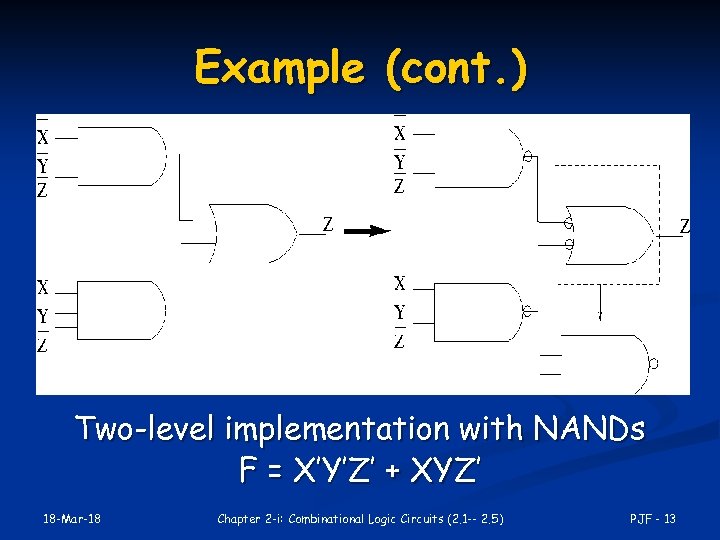
Example (cont. ) Two-level implementation with NANDs F = X’Y’Z’ + XYZ’ 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 13

Multilevel NAND Circuits Starting from a multilevel circuit: 1. Convert all AND gates to NAND gates with AND-NOT graphic symbols. 2. Convert all OR gates to NAND gates with NOT-OR graphic symbols. 3. Check all the bubbles in the diagram. For every bubble that is not counteracted by another bubble along the same line, insert a NOT gate or complement the input literal from its original appearance. 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 14
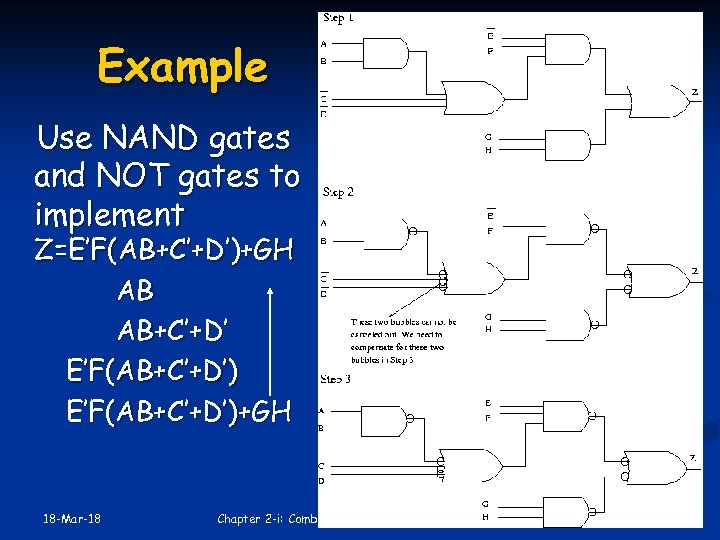
Example Use NAND gates and NOT gates to implement Z=E’F(AB+C’+D’)+GH AB AB+C’+D’ E’F(AB+C’+D’)+GH 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 15
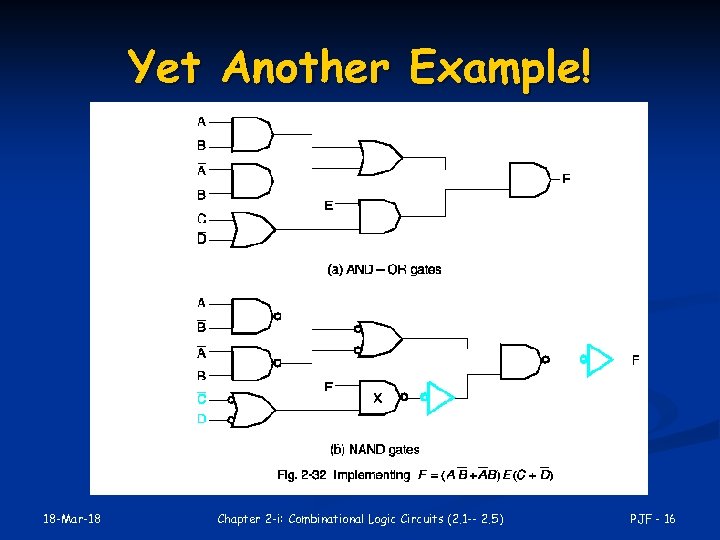
Yet Another Example! 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 16

NOR Gate Also a “universal” gate because ANY digital circuit can be implemented with NOR gates alone. n This can be similarly proven as with the NAND gate n 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 17

NOR Circuits n To easily derive a NOR implementation of a boolean function: n n 18 -Mar-18 Find a simplified POS is an OR-AND circuit Change OR-AND circuit to a NOR circuit Use the alternative symbols below Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 18

Two-Level NOR Gate Implementation - Example F(X, Y, Z) = m(0, 6) 1. Express F’ in SOP form: 1. 2. 3. 4. F’ = m(1, 2, 3, 4, 5, 7) = X’Y’Z + X’YZ’ + X’YZ + XY’Z’ + XY’Z + XYZ F’ = XY’ + X’Y + Z Take the complement of F’ to get F in the POS form: F = (F’)' = (X'+Y)(X+Y')Z' Obtain the OR-AND implementation for F. Add bubbles and inverters to transform OR-AND implementation to NOR-NOR implementation. 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 19
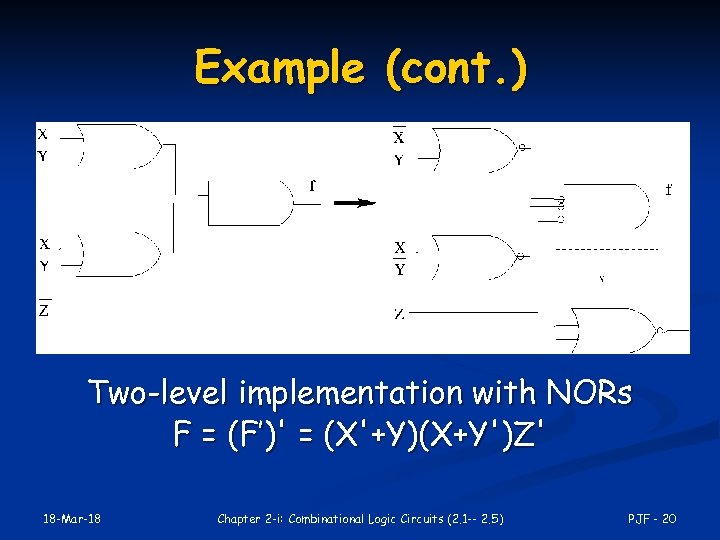
Example (cont. ) Two-level implementation with NORs F = (F’)' = (X'+Y)(X+Y')Z' 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 20

Multilevel NOR Circuits Starting from a multilevel circuit: 1. Convert all OR gates to NOR gates with OR-NOT graphic symbols. 2. Convert all OR gates to NOR gates with NOT-AND graphic symbols. 3. Check all the bubbles in the diagram. For every bubble that is not counteracted by another bubble along the same line, insert a NOT gate or complement the input literal from its original appearance. 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 21

Exclusive-OR (XOR) Function n XOR (also ) : the “not-equal” function XOR(X, Y) = X Y = X’Y + XY’ Identities: n n n Properties: n n 18 -Mar-18 X 0=X X 1 = X’ X X=0 X X’ = 1 X Y=Y X (X Y) W = X ( Y W) Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 22

XOR function implementation XOR(a, b) = ab’ + a’b n Straightforward: 5 gates n 2 inverters, two 2 -input ANDs, one 2 -input OR n 2 inverters & 3 2 -input NANDs n n Nonstraightforward: n 18 -Mar-18 4 NAND gates Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 23
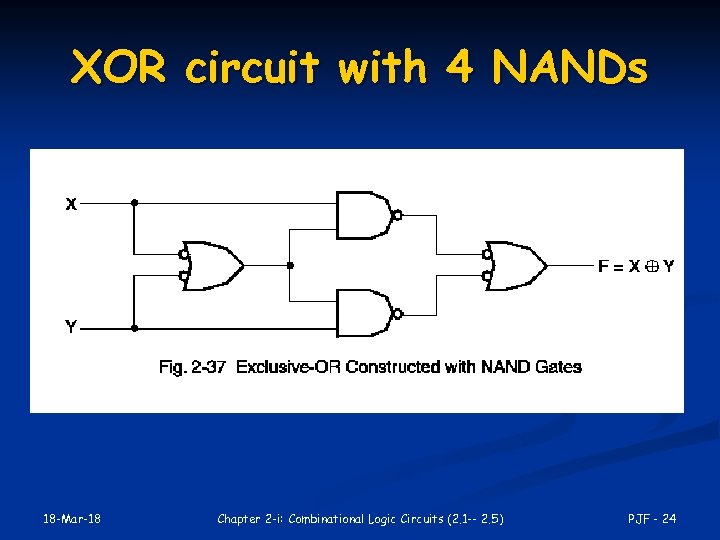
XOR circuit with 4 NANDs 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 24

Exclusive-NOR (XNOR) Function XNOR: the “equality” function n XNOR(a, b) = ab + a’b’ n Observe that XNOR(a, b) = ( XOR(a, b) )’ n n n ( a b )’ = ( a’b + ab’)’ = (a’b)’ (ab’)’ = (a + b’) (a’ +b) = ab + a’b’ a b’ = ( a b )’ = a’ b 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 25

Odd Function x y = x’y + xy’ n x y z = xy’z’ + x’y’z +xyz n x y z w = x’yzw + xy’zw + xyz’w + xyzw’ + x’y’z’w + x’yz’w’ + x’y’zw’ +xy’z’w’ n … Observe a pattern here? n An n-input XOR function is implied (=1) by all the minterms that have an odd # of 1 s n Thus, XOR is also know as the odd function n 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 26
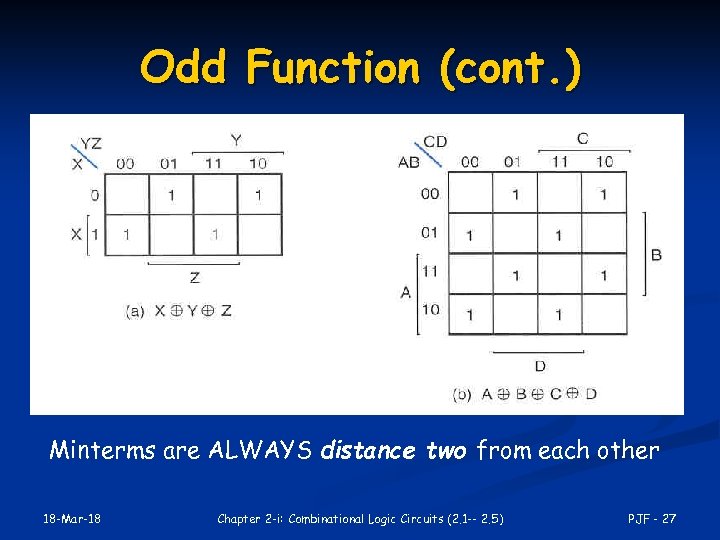
Odd Function (cont. ) Minterms are ALWAYS distance two from each other 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 27
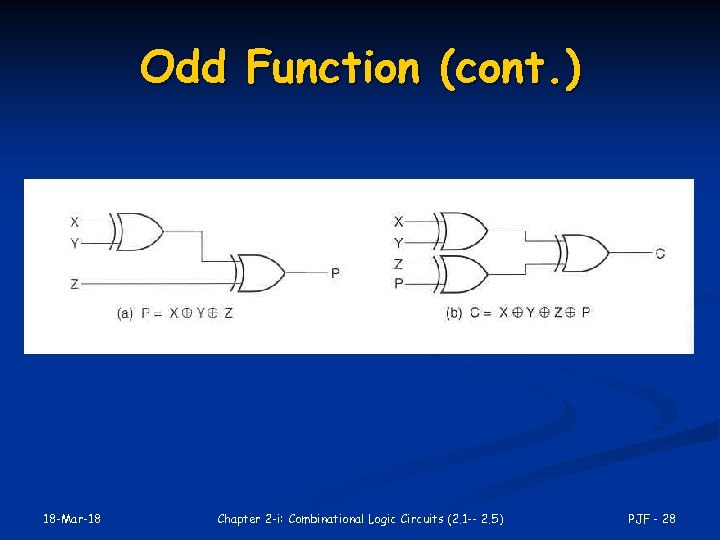
Odd Function (cont. ) 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 28

Even Function n How would you implement an even function? The complement of XOR XNOR 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 29

Parity Generation and Checking Odd and even functions can be used to implement parity checking circuits used for error detection and correction. n Use even parity as example. n Parity generator: the circuit that generates the parity bit before transmitting. n Parity checker: the circuit that checks the parity in the receiver. n 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 30

Even Parity Generation n n P(X, Y, Z) must produce a 1 for all the input combinations that contain an odd number of 1 s Thus, it is a 3 -input odd function P = X Y Z 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 31

Even Parity Checking How would you implement a parity checker for the previous example? Use a 4 -input XOR circuit (odd function) C = X Y Z P 1 indicates an error OR A 4 -input XNOR circuit (even function) C = (X Y Z P)’ 1 indicates a pass 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 32
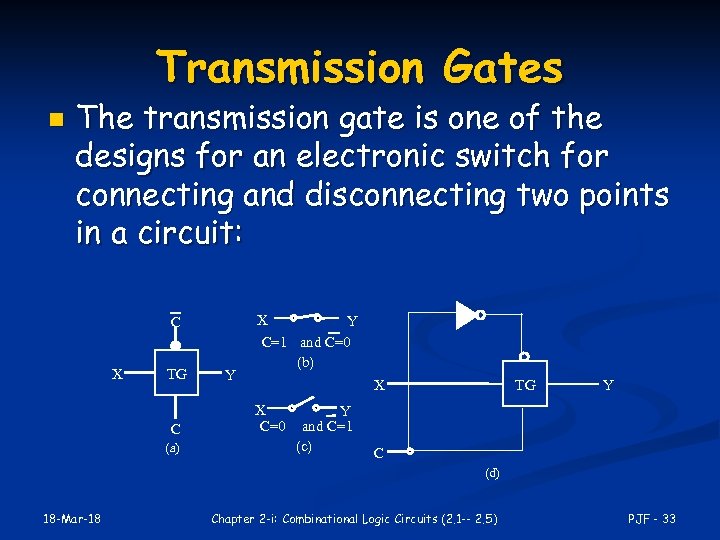
Transmission Gates n The transmission gate is one of the designs for an electronic switch for connecting and disconnecting two points in a circuit: X C X TG C (a) Y Y C=1 and C=0 (b) X X C=0 Y and C=1 (c) TG Y C (d) 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 33

Transmission Gates (continued) n n In many cases, X can be regarded as a data input and Y as an output. C and C, with complementary values applied, is a control input. With these definitions, the transmission gate, provides a 3 state output: n n n C = 1, Y = X (X = 0 or 1) C = 0, Y = Hi-Z Care needs to be taken when using the TG in design, however, since X and Y as input and output are interchangeable, and signals can pass in both directions. 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 34
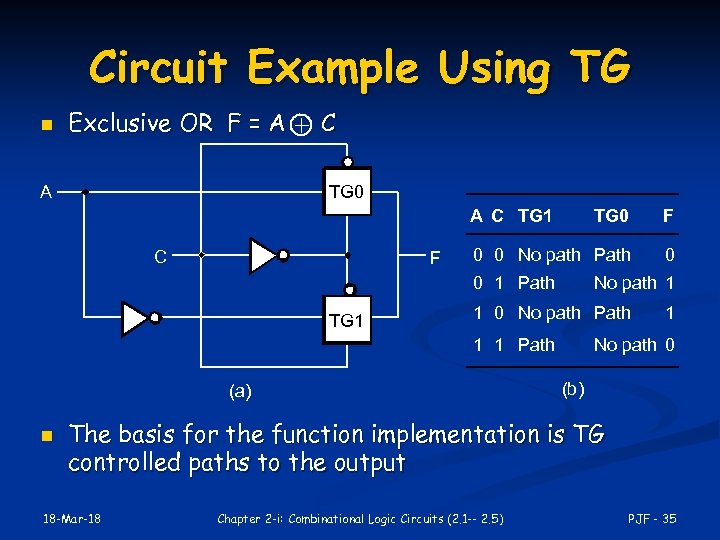
Circuit Example Using TG n Exclusive OR F = A + C A TG 0 A C TG 1 C F TG 0 F 0 0 No path Path 0 0 1 Path TG 1 No path 1 1 0 No path Path 1 1 Path (a) n 1 No path 0 (b) The basis for the function implementation is TG controlled paths to the output 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 35

More Complex Gates n n The remaining complex gates are SOP or POS structures with and without an output inverter. The names are derived using: n n 18 -Mar-18 A - AND O - OR I - Inverter Numbers of inputs on first-level “gates” or directly to second-level “gates” Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 36

More Complex Gates (continued) n n Example: AOI - AND-OR-Invert consists of a single gate with AND functions driving an OR function which is inverted (page 95 in the textbook). These gate types are used because: n n 18 -Mar-18 The number of transistors needed is fewer than required by connecting together primitive gates Potentially, the circuit delay is smaller, increasing the circuit operating speed Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 37

Terms of Use n n n © 2004 by Pearson Education, Inc. All rights reserved. The following terms of use apply in addition to the standard Pearson Education Legal Notice. Permission is given to incorporate these materials into classroom presentations and handouts only to instructors adopting Logic and Computer Design Fundamentals as the course text. Permission is granted to the instructors adopting the book to post these materials on a protected website or protected ftp site in original or modified form. All other website or ftp postings, including those offering the materials for a fee, are prohibited. You may not remove or in any way alter this Terms of Use notice or any trademark, copyright, or other proprietary notice, including the copyright watermark on each slide. Return to Title Page 18 -Mar-18 Chapter 2 -i: Combinational Logic Circuits (2. 1 -- 2. 5) PJF - 38
64ef2b65dca43cf68019b8faa3a2340e.ppt