Единый государственный экзамен по математике 2015 г Методы

Единый государственный экзамен по математике 2015 г. Методы решения уравнений и неравенств Подолян Елена Вячеславовна, кандидат педагогических наук, доцент, председатель ГЭК ЕГЭ по математике по НСО, учитель высшей квалификационной категории

• Структура вариантов профильного уровня ЕГЭ по математике; • методы решения тригонометрических, показательных, логарифмических уравнений, нахождение частных решений (задание № 15); • решение логарифмических неравенств, метод рационализации (задание № 17); • критерии оценивания заданий с развернутым ответом.

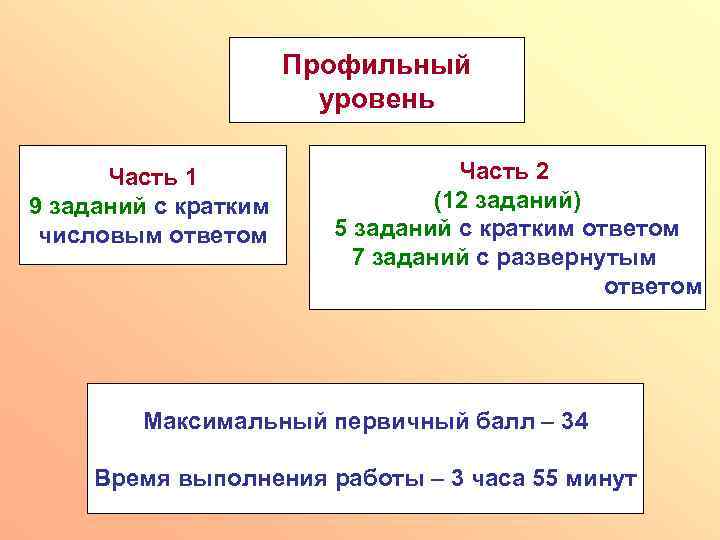Профильный уровень Часть 1 9 заданий с кратким числовым ответом Часть 2 (12 заданий) 5 заданий с кратким ответом 7 заданий с развернутым ответом Максимальный первичный балл – 34 Время выполнения работы – 3 часа 55 минут

Часть 2 15. 1 а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку Ответ:

Содержание критерия задачи № 15 Обоснованно получены верные ответы в обоих пунктах Обоснованно получен верный ответ в пункте а или в пункте б ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения Решение не соответствует ни одному из критериев, перечисленных выше Максимальный балл Баллы 2 1 0 2

15. 2 а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку Решение. а) Запишем уравнение в виде:

Значит, или , откуда б) Отбор корней может быть обоснован любым способом: с помощью числовой окружности, с помощью графика, решения двойных неравенств и т. д. Ответ: а) б)

15. 3 а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку Ответ: а) б)

15. 4 а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие отрезку

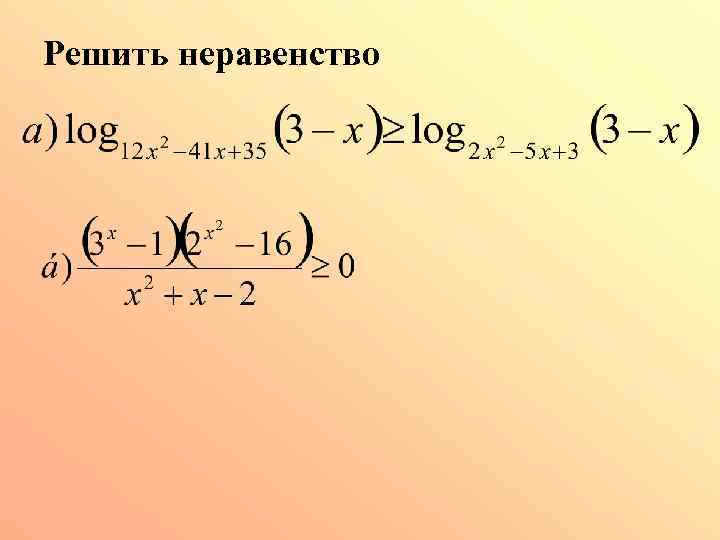Решить неравенство

Метод рационализации (метод интервалов) при решении логарифмических и показательных неравенств

Неравенства, содержащие логарифм с постоянным основанием Рассмотрим неравенство Теорема 1. При любом допустимом основании ( ) имеет место равносильность: на ОДЗ исходного неравенства.

Следствие. Если , то на ОДЗ исходного неравенства. Из формул (1), (2) следуют правила П 1, П 2.

Правило 1. При любом допустимом основании и любых положительных функциях и знак разности совпадает со знаком произведения

Пример 17. 1 Решите неравенство Ответ:

Правило 2. Знак выражения совпадает со знаком произведения на ОДЗ.

Пример 17. 2 Решите неравенство Ответ:

Неравенства, содержащие логарифм с переменным основанием Рассмотрим выражение По определению, для любого полагают, что ,

Теорема 3. При любых положительных функциях и , имеет место равносильность:

Следствие. Если , то на ОДЗ исходного неравенства. Из формул (3), (4) следуют правила П 3, П 4.

Правило 3. Знак разности совпадает со знаком произведения на ОДЗ. Правило 4. Знак совпадает со знаком произведения на ОДЗ.

Пример 17. 3 Решите неравенство Ответ.

Пример 17. 4 Решите неравенство Ответ.

Пример 17. 5 Решите неравенство Ответ.

Показательные неравенства 27

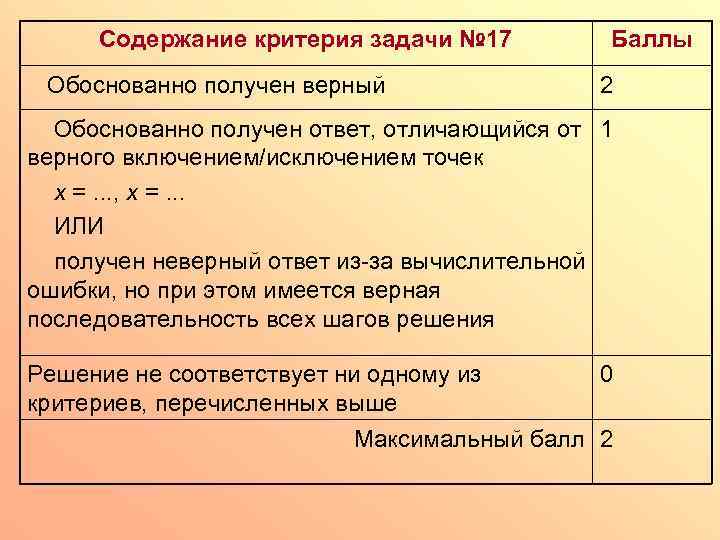Содержание критерия задачи № 17 Обоснованно получен верный Баллы 2 Обоснованно получен ответ, отличающийся от 1 верного включением/исключением точек х =. . . , х =. . . ИЛИ получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения Решение не соответствует ни одному из 0 критериев, перечисленных выше Максимальный балл 2

Пример 17. 6 Решите неравенство Ответ: -1 Пример 17. 7 Решите неравенство Ответ: