9ce35590087909c59e89a361538a9941.ppt
- Количество слайдов: 44
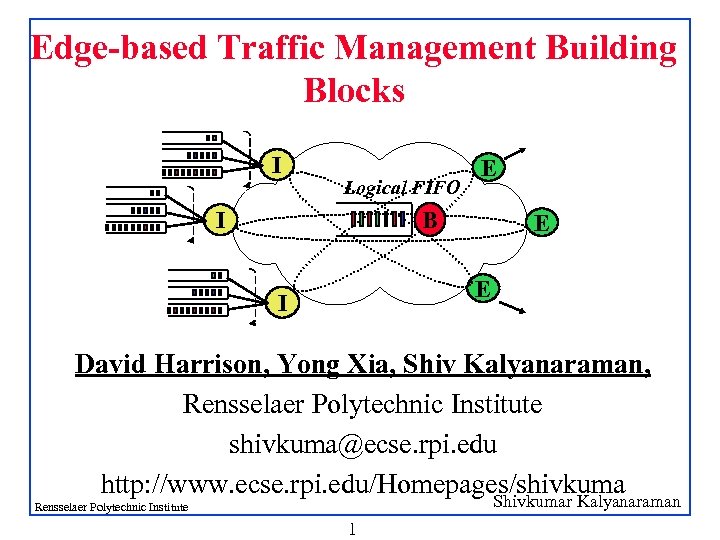
Edge-based Traffic Management Building Blocks I Logical FIFO E B I E E I David Harrison, Yong Xia, Shiv Kalyanaraman, Rensselaer Polytechnic Institute shivkuma@ecse. rpi. edu http: //www. ecse. rpi. edu/Homepages/shivkuma Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 1

Overview q Private Networks vs Public Networks q Qo. S vs Congestion Control: the middle ground ? q Overlay Bandwidth Services: q Key: deployment advantages q A closed-loop Qo. S building block q Services: Better best-effort services, Assured services, Quasileased lines, App-level Qo. S… Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 2
Motivation: Site-to-Site VPN Over a Multi-Provider Internetwork Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 3
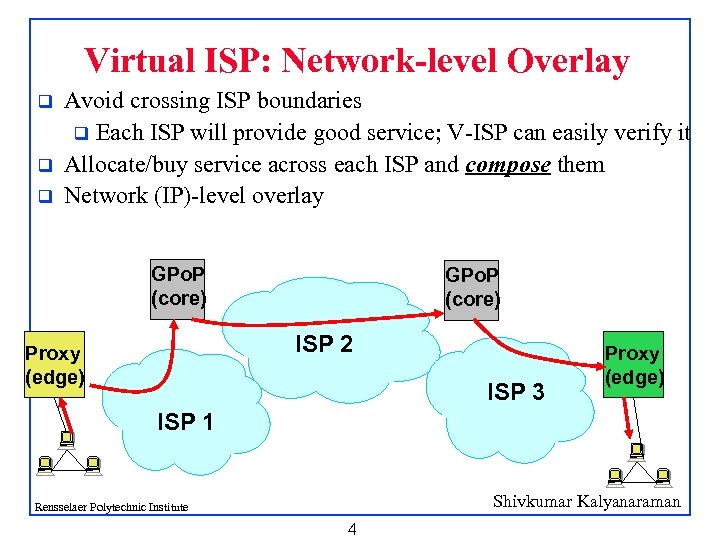
Virtual ISP: Network-level Overlay q q q Avoid crossing ISP boundaries q Each ISP will provide good service; V-ISP can easily verify it Allocate/buy service across each ISP and compose them Network (IP)-level overlay GPo. P (core) ISP 2 Proxy (edge) ISP 3 Proxy (edge) ISP 1 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 4

Our Model: Edge-based building blocks I Logical FIFO E B I E E I New: Closed-loop control ! Policy/ Bandwidth Broker Model: Inspired by diff-serv; Aim: further interior simplification Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 5

Closed-loop BB: Bandwidth Sharing Priority/WFQ B FIFO B Scheduler: differentiates service on a packet-bypacket basis q Loops: differentiate service on an RTT-by-RTT basis using edge-based policy configuration. q Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 6
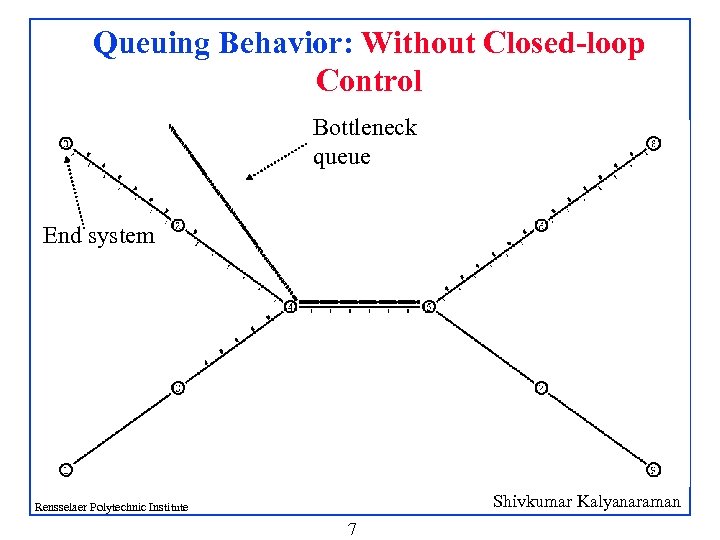
Queuing Behavior: Without Closed-loop Control Bottleneck queue End system Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 7
Queuing: With Closed Loops q q Bottleneck management issues consolidated at edges q Key: Transparent and lossless loop schemes Potential: q Edge-based Qo. S services, q Edge plays in application-level Qo. S, active networking. . Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 8

Closed-loop Building Block Reqts #1. Edge-to-edge overlay operation, #2. Robust stability #3. Bounded-buffer/zero-loss, #4. Minimal configuration/upgrades + incremental deployment #5. Rate-based operation: for bandwidth services Not available in any congestion control scheme… q Related work: NETBLT, TCP Vegas, Mo/Walrand, ATM Rate/Credit approaches q Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 9
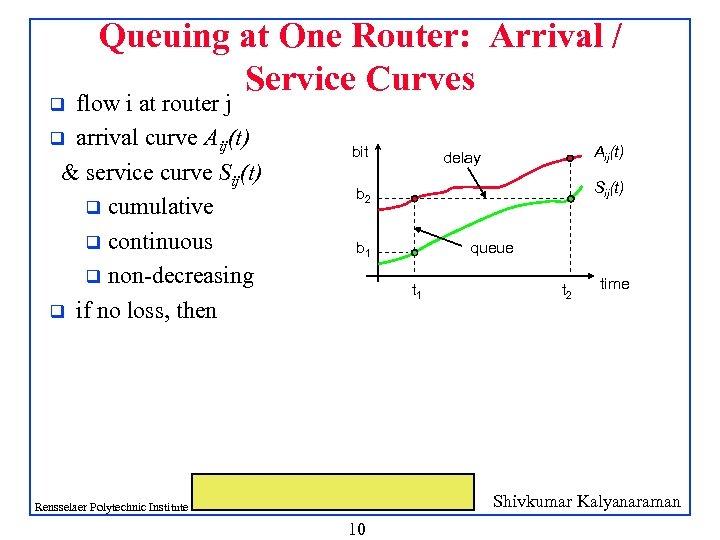
Queuing at One Router: Arrival / Service Curves flow i at router j q arrival curve Aij(t) & service curve Sij(t) q cumulative q continuous q non-decreasing q if no loss, then q bit Aij(t) delay Sij(t) b 2 b 1 queue t 1 t 2 time Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 10
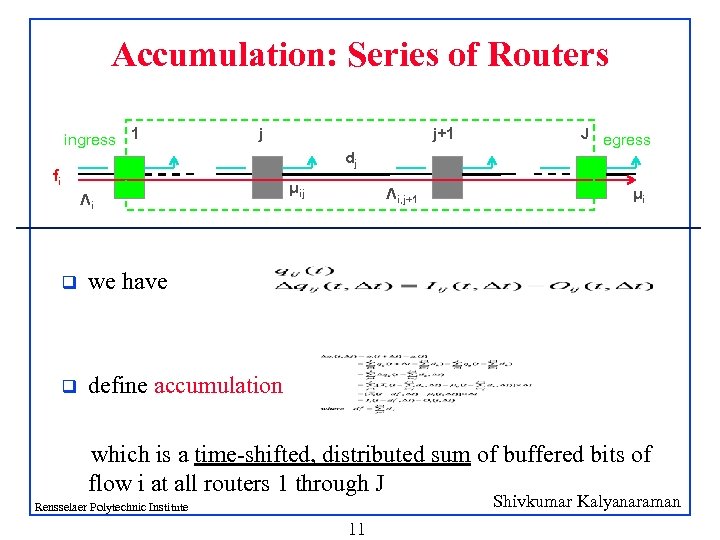
Accumulation: Series of Routers ingress 1 j j+1 J egress dj fi Λi q Λi, j+1 μi we have q μij define accumulation which is a time-shifted, distributed sum of buffered bits of flow i at all routers 1 through J Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 11
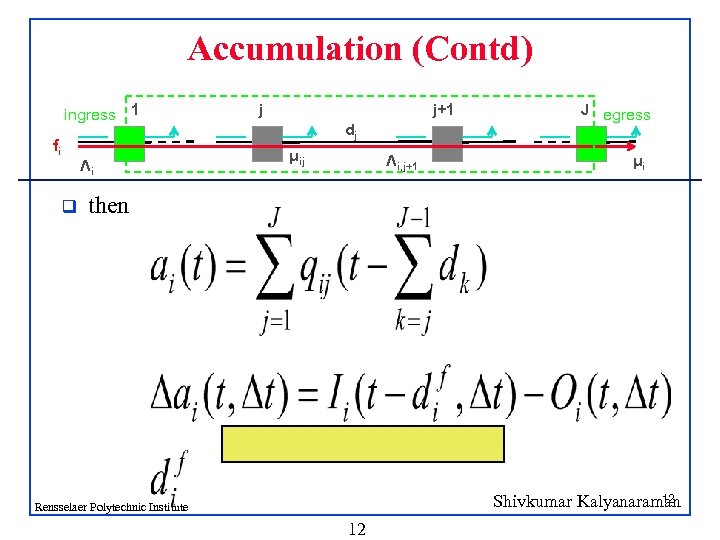
Accumulation (Contd) ingress 1 fi q Λi j j+1 dj μij Λi, j+1 J egress μi then 12 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 12
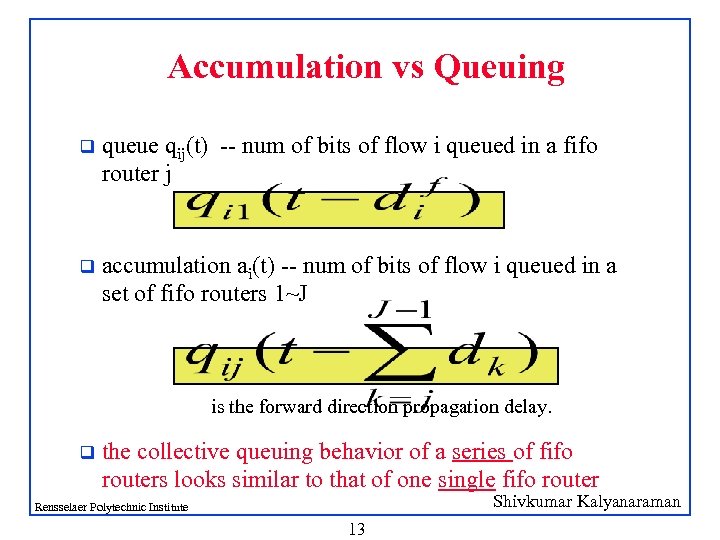
Accumulation vs Queuing q queue qij(t) -- num of bits of flow i queued in a fifo router j q accumulation ai(t) -- num of bits of flow i queued in a set of fifo routers 1~J is the forward direction propagation delay. q the collective queuing behavior of a series of fifo routers looks similar to that of one single fifo router Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 13

Accumulation: Physical Meaning 1 j j+1 J dj fi μij Λi Λi, j+1 μi … 1 Rensselaer Polytechnic Institute … j time 14 j+1 J Shivkumar Kalyanaraman 14
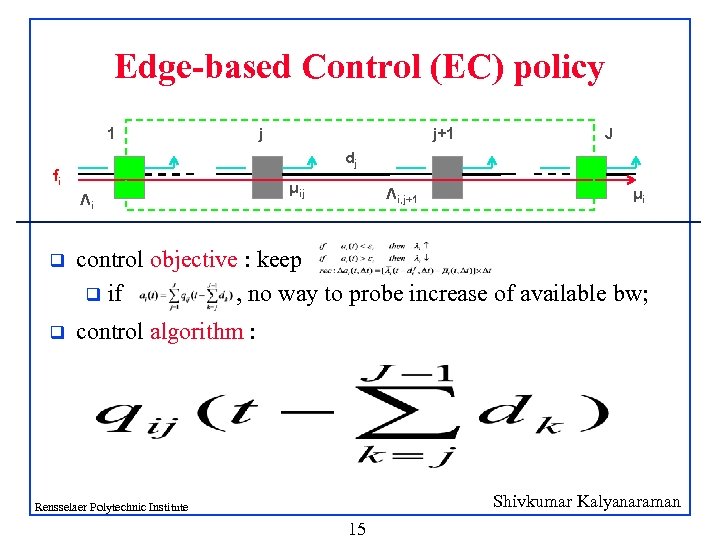
Edge-based Control (EC) policy 1 j j+1 J dj fi Λi μij Λi, j+1 μi q control objective : keep q if , no way to probe increase of available bw; q control algorithm : Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 15

EC schemes monaco q accumulation estimation: out-of-band / in-band q congestion response: additive inc/additive dec (aiad), etc q vegas q accumulation estimation: in-band q congestion response: additive inc / additive dec (aiad) q riviera q accumulation estimation: in-band q congestion response: additive inc / multiplicative dec using egress rate (aimd-er) q 16 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 16

Recall: accumulation theory … 1 Rensselaer Polytechnic Institute … j time 17 j+1 J Shivkumar Kalyanaraman
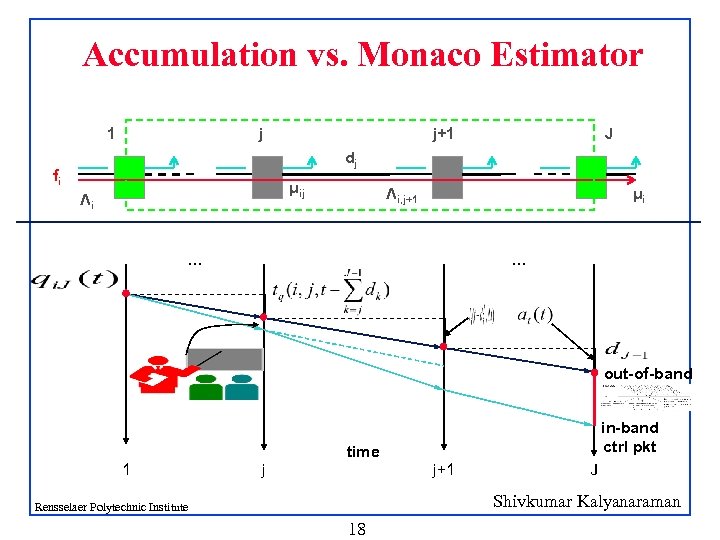
Accumulation vs. Monaco Estimator 1 j j+1 J dj fi μij Λi Λi, j+1 μi … … out-of-band in-band ctrl pkt time 1 j j+1 J Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 18
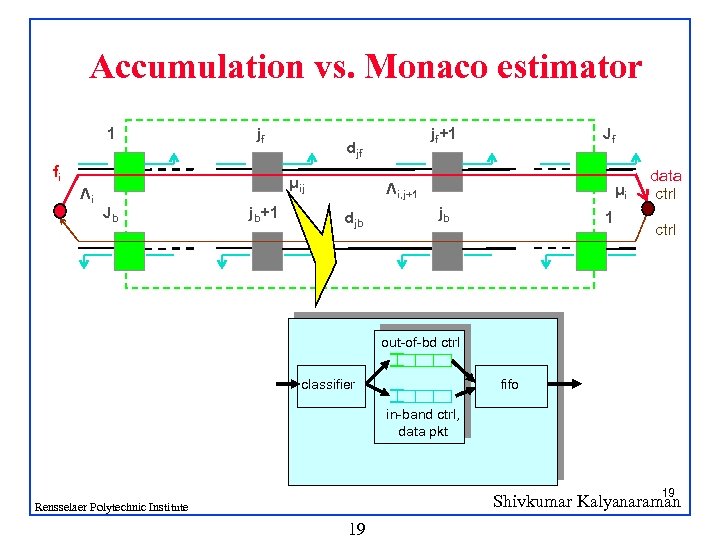
Accumulation vs. Monaco estimator 1 jf fi Λi djf μij Jb jb+1 jf+1 Jf Λi, j+1 djb μi jb 1 data ctrl out-of-bd ctrl classifier fifo in-band ctrl, data pkt 19 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 19

ec: monaco q congestion estimation: q out-of-band q congestion and in-band control packets response: (AIAD) q if qm < α, cwnd(k+1) = cwnd(k) + 1; q if qm > β, cwnd(k+1) = cwnd(k) – 1; [ 1 = α < β = 3 ] 20 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 20

ec: vegas cwnd congestion avoidance slow start q congestion Time estimation: q define qv = ( cwnd / rttp – cwnd / rtt ) * rttp; where rttp is round trip propagation delay (basertt) q congestion response: q if qv < α, cwnd(k+1) = cwnd(k) + 1; q if qv > β, cwnd(k+1) = cwnd(k) – 1; Rensselaer Polytechnic Institute 21 [1=α<β=3] Shivkumar Kalyanaraman

Vegas Accumulation Estimator q the physical meaning of qv q rtt = rttp + rttq [ rttq is queuing time ] q qv = ( cwnd / rttp – cwnd / rtt ) * rttp = ( cwnd / rtt ) * ( rtt – rttp ) = ( cwnd / rtt ) * rttq [ if rtt is typical ] = sending rate * rttq [ little’s law ] = packets backlogged [ little’s law again ] so vegas maintains α ~ β number of packets queued inside the network q it adjusts sending rate additively to achieve this q 22 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 22

Accumulation vs. Vegas estimator 1 fi q Λi jf μij Jb jb+1 jf+1 djf Jf Λi, j+1 djb jb μi 1 data ack Backlogv 23 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 23

Vegas vs. Monaco estimators q Vegas accumulation estimator q ingress-based q round trip (forward data path and backward ack path) q sensitive to ack path queuing delay q sensitive to round trip propagation delay measurement error q Monaco accumulation estimator q egress-based q one way (only forward data path) q insensitive to ack path queuing delay q no need to explicitly know one way propagation delay Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 24

Riviera congestion estimation: q in-band techniques, similar as vegas q congestion response: q 25 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 25
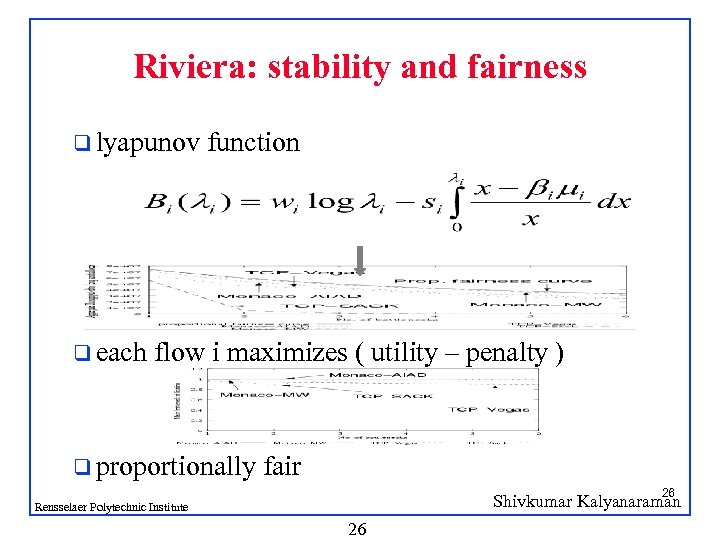
Riviera: stability and fairness q lyapunov q each function flow i maximizes ( utility – penalty ) q proportionally fair 26 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 26

Linear Network Topology 8 U U 8 U En 0 E 0 U Bn E 1 U E 2 U 100 Mbps I 1 B 0 I 00 send rate (Mbps) I 10 U U 8 I 2 4 ms B 1 8 8 U E 00 I 0 U All links are 4 ms, 100 Mbps. I=ingress, E=egress, U=UDP, B=Bottleneck 27 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 27

Stability and Fairness 28 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 28

Utilization 29 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 29
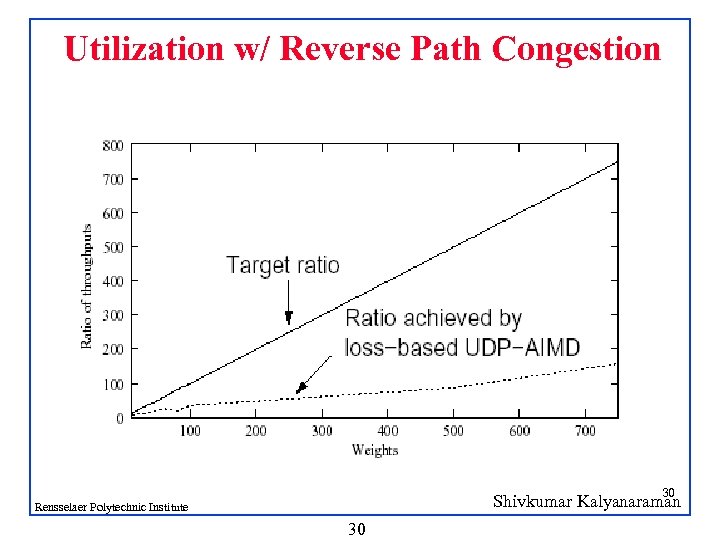
Utilization w/ Reverse Path Congestion 30 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 30
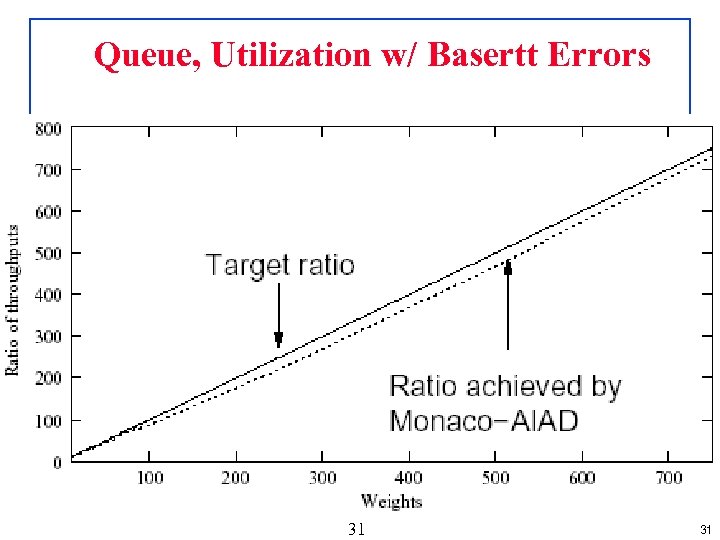
Queue, Utilization w/ Basertt Errors Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 31 31

Service Differentiation: Loss-based or Accumulation-based ? 32 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 32

Overlay Edge-to-edge Bandwidth Services q Idea: Use the EC scheme as a closed-loop building block for a range of Qo. S services q Basic Services: no admission control q “Better” best-effort services q Denial-of-service attack isolation support q Weighted proportional/priority services q Advanced services: edge-based admission control q Assured service emulation q “Quasi-leased-line” service q Key: no upgrades; only configuration reqts… Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 33
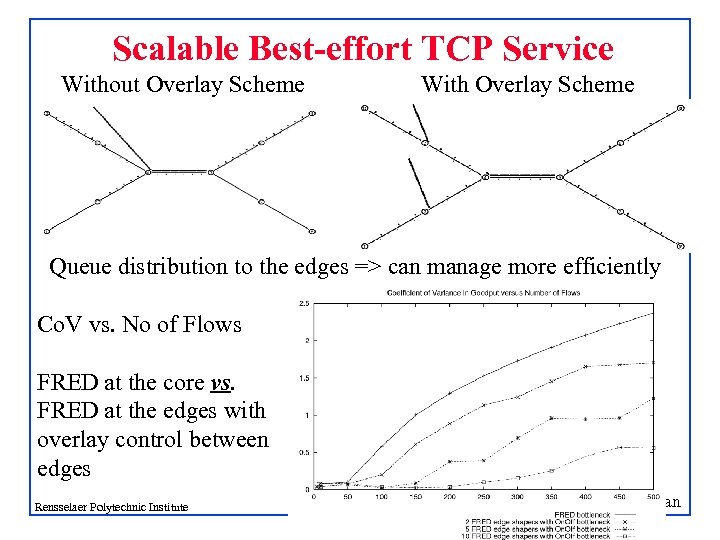
Scalable Best-effort TCP Service Without Overlay Scheme With Overlay Scheme Queue distribution to the edges => can manage more efficiently Co. V vs. No of Flows FRED at the core vs. FRED at the edges with overlay control between edges Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 34

Scalable Best-effort TCP Service Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 35
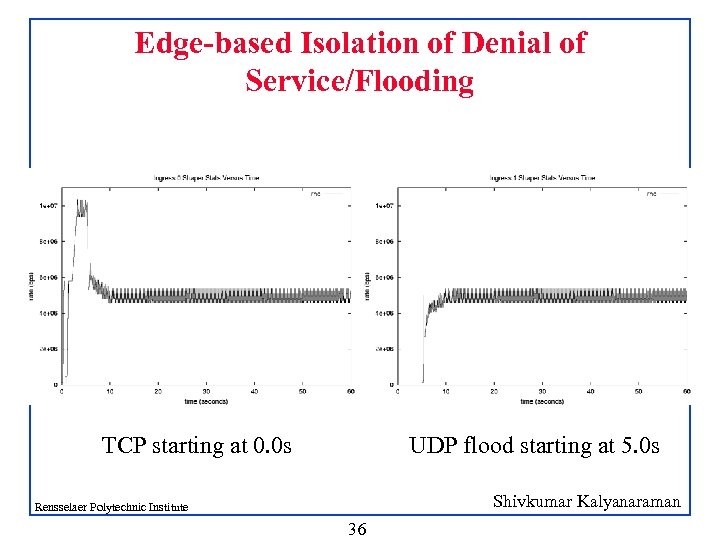
Edge-based Isolation of Denial of Service/Flooding TCP starting at 0. 0 s UDP flood starting at 5. 0 s Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 36

Edge-based Assured Service Emulation q Backoff Differentiation Policy: r= if no congestion r+D min(r, b. AS m, b. BE(m-a)+a) if congestion 1 > b. AS > b. BE >> 0 q q Backoff little (bas) when below assurance (a), Backoff (bas) same as best effort when above assurance (a) Backoff differentiation quicker than increase differentiation Service could be potentially oversubscribed (like frame-relay) q Unsatisfied assurances just use heavier weight. Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 37

Bandwidth Assurances Flow 1 with 4 Mbps assured + 3 Mbps best effort Flow 2 with 3 Mbps best effort Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 38

Quasi-Leased Line (QLL) q q Assume admission control and route-pinning (MPLS LSPs). Provide bandwidth guarantee. Key: No delay or jitter guarantees! q Adaptation in O(RTT) timescales q Average delay can be managed by limiting total and per. VL allocations (managed delay) Policy: r= r+D if no congestion max(a, b. BE(m-a)+a) if congestion 1 > b. BE >> 0 Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 39

Quasi-Leased Line Example Best-effort VL starts at t=0 and fully utilizes 100 Mbps bottleneck. Best-effort rate limit versus time Background QLL starts with rate 50 Mbps Best-effort VL quickly adapts to new rate. Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 40

Quasi-Leased Line Example (cont) Bottleneck queue versus time Starting QLL incurs backlog. Unlike TCP, VL traffic trunks backoff without requiring loss and without bottleneck assistance. Requires more buffers: larger max queue Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 41

Quasi-Leased Line (cont. ) Worst-case queue vs Fraction of capacity for QLLs Single bottleneck analysis: b B/w-delay q< 1 -b products For b=. 5, q=1 bw-rtt Simulated QLL w/ edge-to-edge control. Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 42

Current Work q With bottlenecks consolidated at the edge: q What diff-serv PHBs or remote scheduler functionalities can be emulated from the edge ? q What is the impact of congestion control properties and rate of convergence on attainable set of services ? q Areas: q Control plane architecture for large-scale overlays q Application-level Qo. S: edge-to-end problem q Dynamic (short-term) services q Congestion-sensitive pricing: congestion info at the edge q Edge-based contracting/bidding frameworks Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 43

Summary q Private Networks vs Public Networks q Qo. S vs Congestion Control vs Throwing bandwidth q Edge-based Building Blocks & Overlay services: q A closed-loop Qo. S building block: EC framework q Accumulation concept q Monaco, Vegas, Riviera Schemes: estimation issues q Basic services, advanced services Shivkumar Kalyanaraman Rensselaer Polytechnic Institute 44
9ce35590087909c59e89a361538a9941.ppt