Edge-Based Reconstruction Schemes in CFD and CAA Ilya

Edge-Based Reconstruction Schemes in CFD and CAA Ilya ABALAKIN, Tatiana KOZUBSKAYA CAA Laboratory of Keldysh Institute of Applied Mathematics of RAS, Moscow, Russia Pavel BAKHVALOV Moscow Institute of Physics and Technology, Dolgoprudny, Russia The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 1

Outline Basic 1 D high accuracy scheme Introduction Scheme for linear transport equation on uniform meshes Scheme for linear transport equations on non-uniform meshes Scheme for nonlinear hyperbolic equation EBR schemes for unstructured meshes Conservative vertex-centred formulation Edge-Based Reconstruction on translationally symmetric meshes Edge-Based Reconstruction on arbitrary triangular/tetrahedral meshes Meshes providing the highest theoretically reachable order of accuracy Numerical illustrations WENO-EBR schemes Basic 1 D WENO scheme WENO-EBR Scheme for unstructured meshes Numerical illustrations Concluding remarks Numerical results The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 2

Introduction Nowadays high accuracy of CFD and, especially, CAA is of strong demand from industry Unstructured meshes become more and more attractive Two main streams: FE, mostly DG and FV polynomial-based schemes compete Both are still rather expensive, to be widely used for solving applied problems EBR (Edge-Based Reconstruction) schemes provide a good compromise as a low. ER cost and high. ER accuracy numerical method EBR schemes efficiency is particularly evident in the nonlinear case when shock-capturing techniques are to be implemented The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 3

Basic 1 D high accuracy scheme Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 5

Basic 1 D high accuracy scheme Linear transport equation Uniform mesh Semi-discrete approximation Uniform mesh Computational cell Vertex-centered approach should be defined The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 6

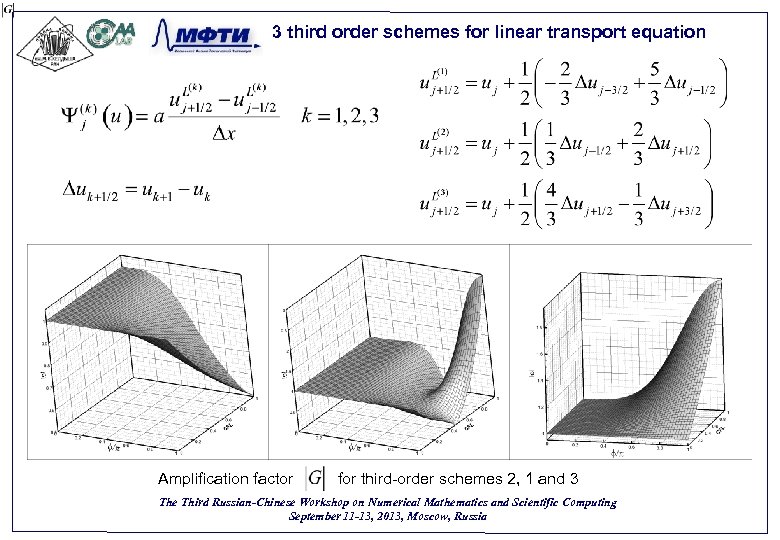
3 third order schemes for linear transport equation Amplification factor for third-order schemes 2, 1 and 3 The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 7

Fifth order scheme for linear transport equation Amplification factor fifth-order scheme Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 9

Fifth order scheme for linear transport equation Linear transport equation Positive/negative advection velocity Semi-discrete approximation The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 10

Basic 1 D high accuracy scheme Linear transport equation Non-uniform mesh Semi-discrete approximation Non-uniform mesh Computational cell Such representation coincides with HO approximation on uniform mesh (i) and is exact for linear functions (ii) The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 11

Basic 1 D high accuracy scheme Nonlinear equation Semi-discrete approximation Numerical flux is defined by the Reimann solver. Consider two options: Remark The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia hybrid 12

EBR schemes for unstructured meshes The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 13

Conservative vertex-centred formulation Euler equations Vertex-centred formulation implies the existence of cells corresponding to the mesh nodes (vertices). - cell around vertex i - its volume - its boundary - neighbors of vertex i The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 14

Conservative vertex-centred formulation Under the rectangular rule - numerical flux defined with the help of some Riemann solver (Roe or Huang or hybrid solver in our case) is somewhat defined in single point of intersection of cell face ik with the edge ik ● ● ● - sum of oriented areas of subfaces of face ik The problem of scheme construction is reduced to the problem of definition (approximation) of in red points The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 15

Reconstruction on translationally symmetric meshes Def. : A mesh is said to be translationally symmetric (TS) if it is translationally invariant with respect to the vectors of all edges of the mesh How do they look like? For instance, they can be built by skewing “Cartesian” mesh The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 16

Translationally symmetric (TS) meshes The edges of TS meshes form 3 groups of equal-spaced parallel lines (in 2 D) Not only triangles in 2 D, parallelograms are still possible In 3 D, tetrahedral TS-meshes can be produced by any linear transformation of cubes decomposed uniformly into six tetrahedrons. A set of tetrahedrons included to the cube is characterized by seven different edges, so that the TS-mesh remains the same with respect to translation on each of them. The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 17

1 D HO Reconstruction on TS-meshes - 6 -points stencil of 1 d HO interpolation Numerical flux can be defined with the help of left (L) and right (R) reconstructed values: Such reconstruction coincides with HO reconstruction on uniform mesh (1) and is exact for linear functions (2) The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 18

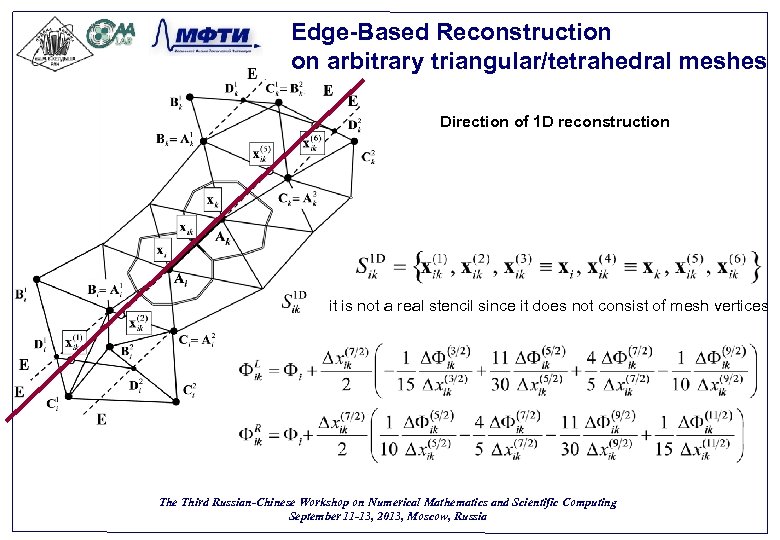
Edge-Based Reconstruction on arbitrary triangular/tetrahedral meshes Direction of 1 D reconstruction it is not a real stencil since it does not consist of mesh vertices The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 19

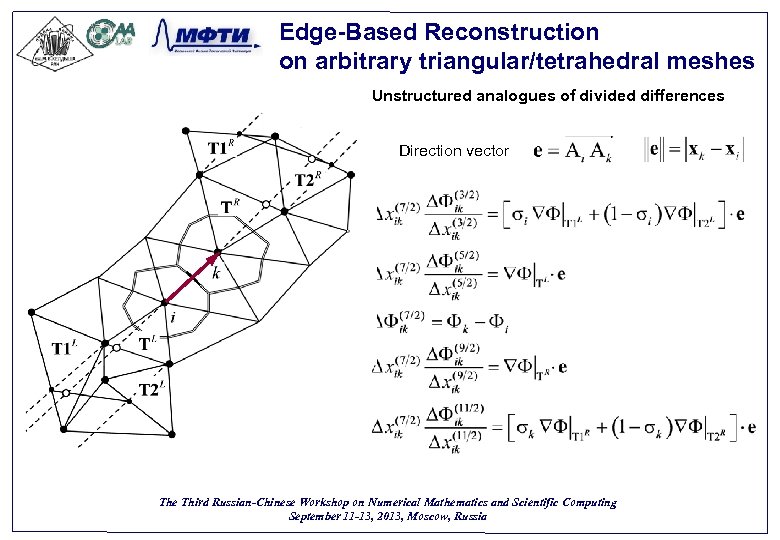
Edge-Based Reconstruction on arbitrary triangular/tetrahedral meshes Unstructured analogues of divided differences Direction vector The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 20

Edge-Based Reconstruction on arbitrary triangular/tetrahedral meshes Quasi-1 D reconstruction Stencil of quasi-1 D reconstruction Def. : A reconstruction is said to be quasi-1 D if the following two conditions are satisfied: 1) the reconstruction coincides with the 1 D HO reconstruction on translational symmetric meshes; 2) the reconstruction coefficients are continuous with respect to the mesh deformation The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 21

Edge-Based Reconstruction on arbitrary triangular/tetrahedral meshes Order of accuracy Theoretical estimation Highest possible theoretical order (of 5 th-6 th) is reachable on the following meshes: 1) translationally symmetric meshes (with the same way of cell construction for each node); 2) “Cartesian”* and other meshes if their cells including the vertices are translationally superposable Examples of translationally superposable barycentric (left) and orthocentric (right) cells Experimental estimation In practice EBR schemes provide high. ER accuracy of order form 2 nd to 5 -6 th depending on mesh quality The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 22

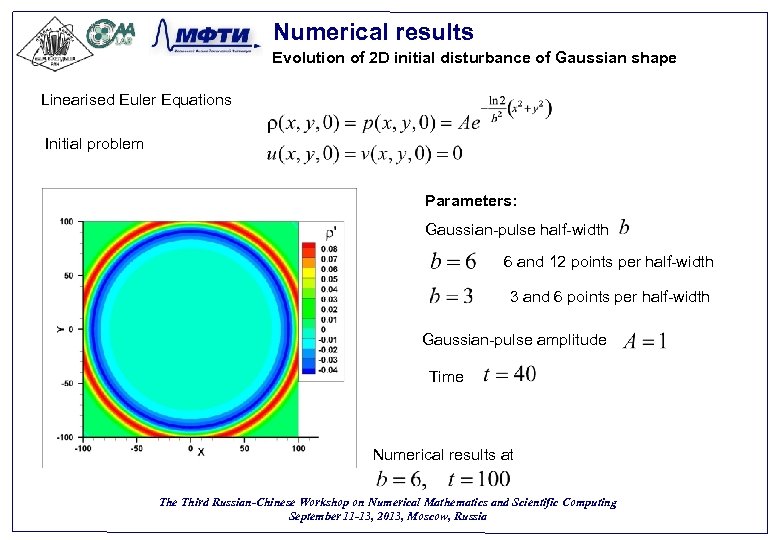
Numerical results Evolution of 2 D initial disturbance of Gaussian shape Linearised Euler Equations Initial problem Parameters: Gaussian-pulse half-width 6 and 12 points per half-width 3 and 6 points per half-width Gaussian-pulse amplitude Time Numerical results at The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 23

Numerical results Experimental estimation of order of accuracy Numerical results obtained on two meshes (coarse and fine) are compared with the exact solution Procedure of refinement The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 24

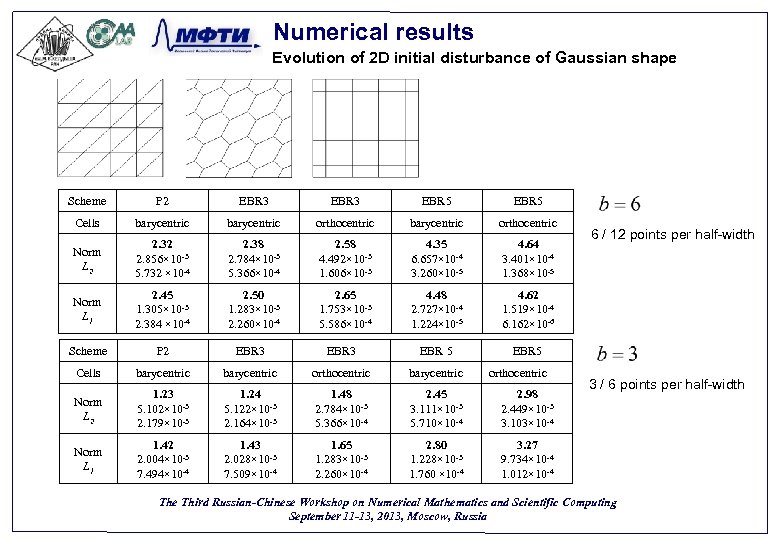
Numerical results Evolution of 2 D initial disturbance of Gaussian shape Scheme P 2 EBR 3 EBR 5 Cells barycentric orthocentric Norm L 2 2. 32 2. 856× 10 -3 5. 732 × 10 -4 2. 38 2. 784× 10 -3 5. 366× 10 -4 2. 58 4. 492× 10 -3 1. 606× 10 -3 4. 35 6. 657× 10 -4 3. 260× 10 -5 4. 64 3. 401× 10 -4 1. 368× 10 -5 Norm L 1 2. 45 1. 305× 10 -3 2. 384 × 10 -4 2. 50 1. 283× 10 -3 2. 260× 10 -4 2. 65 1. 753× 10 -3 5. 586× 10 -4 4. 48 2. 727× 10 -4 1. 224× 10 -5 4. 62 1. 519× 10 -4 6. 162× 10 -6 Scheme P 2 EBR 3 EBR 5 Cells barycentric orthocentric barycentric Norm L 2 1. 23 5. 102× 10 -3 2. 179× 10 -3 1. 24 5. 122× 10 -3 2. 164× 10 -3 1. 48 2. 784× 10 -3 5. 366× 10 -4 2. 45 3. 111× 10 -3 5. 710× 10 -4 2. 98 2. 449× 10 -3 3. 103× 10 -4 Norm L 1 1. 42 2. 004× 10 -3 7. 494× 10 -4 1. 43 2. 028× 10 -3 7. 509× 10 -4 1. 65 1. 283× 10 -3 2. 260× 10 -4 2. 80 1. 228× 10 -3 1. 760 × 10 -4 3. 27 9. 734× 10 -4 1. 012× 10 -4 orthocentric 6 / 12 points per half-width 3 / 6 points per half-width The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 25

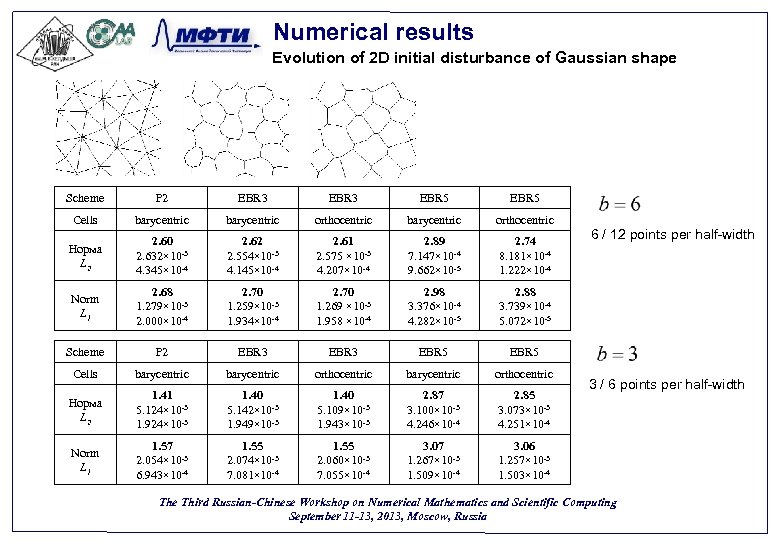
Numerical results Evolution of 2 D initial disturbance of Gaussian shape Scheme P 2 EBR 3 EBR 5 Cells barycentric orthocentric Норма L 2 2. 60 2. 632× 10 -3 4. 345× 10 -4 2. 62 2. 554× 10 -3 4. 145× 10 -4 2. 61 2. 575 × 10 -3 4. 207× 10 -4 2. 89 7. 147× 10 -4 9. 662× 10 -5 2. 74 8. 181× 10 -4 1. 222× 10 -4 Norm L 1 2. 68 1. 279× 10 -3 2. 000× 10 -4 2. 70 1. 259× 10 -3 1. 934× 10 -4 2. 70 1. 269 × 10 -3 1. 958 × 10 -4 2. 98 3. 376× 10 -4 4. 282× 10 -5 2. 88 3. 739× 10 -4 5. 072× 10 -5 Scheme P 2 EBR 3 EBR 5 Cells barycentric orthocentric Норма L 2 1. 41 5. 124× 10 -3 1. 924× 10 -3 1. 40 5. 142× 10 -3 1. 949× 10 -3 1. 40 5. 109× 10 -3 1. 943× 10 -3 2. 87 3. 100× 10 -3 4. 246× 10 -4 2. 85 3. 073× 10 -3 4. 251× 10 -4 Norm L 1 1. 57 2. 054× 10 -3 6. 943× 10 -4 1. 55 2. 074× 10 -3 7. 081× 10 -4 1. 55 2. 060× 10 -3 7. 055× 10 -4 3. 07 1. 267× 10 -3 1. 509× 10 -4 3. 06 1. 257× 10 -3 1. 503× 10 -4 6 / 12 points per half-width 3 / 6 points per half-width The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 26

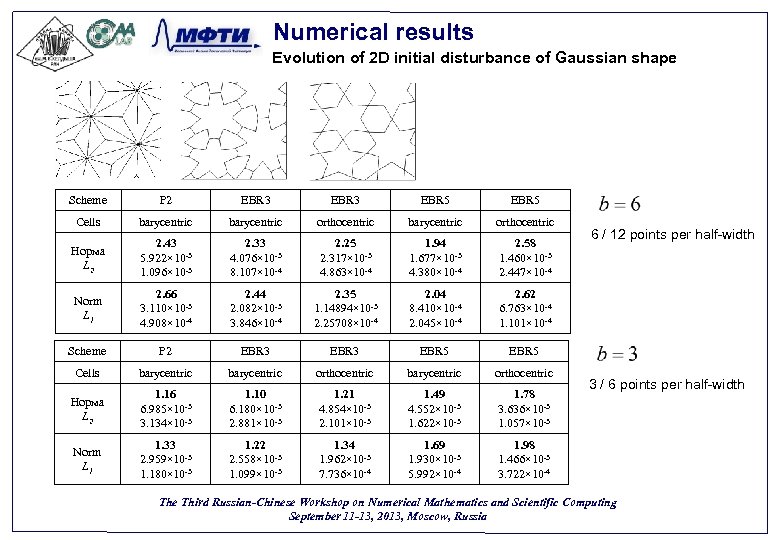
Numerical results Evolution of 2 D initial disturbance of Gaussian shape Scheme P 2 EBR 3 EBR 5 Cells barycentric orthocentric Норма L 2 2. 43 5. 922× 10 -3 1. 096× 10 -3 2. 33 4. 076× 10 -3 8. 107× 10 -4 2. 25 2. 317× 10 -3 4. 863× 10 -4 1. 94 1. 677× 10 -3 4. 380× 10 -4 2. 58 1. 460× 10 -3 2. 447× 10 -4 Norm L 1 2. 66 3. 110× 10 -3 4. 908× 10 -4 2. 44 2. 082× 10 -3 3. 846× 10 -4 2. 35 1. 14894× 10 -3 2. 25708× 10 -4 2. 04 8. 410× 10 -4 2. 045× 10 -4 2. 62 6. 763× 10 -4 1. 101× 10 -4 Scheme P 2 EBR 3 EBR 5 Cells barycentric orthocentric Норма L 2 1. 16 6. 985× 10 -3 3. 134× 10 -3 1. 10 6. 180× 10 -3 2. 881× 10 -3 1. 21 4. 854× 10 -3 2. 101× 10 -3 1. 49 4. 552× 10 -3 1. 622× 10 -3 1. 78 3. 636× 10 -3 1. 057× 10 -3 Norm L 1 1. 33 2. 959× 10 -3 1. 180× 10 -3 1. 22 2. 558× 10 -3 1. 099× 10 -3 1. 34 1. 962× 10 -3 7. 736× 10 -4 1. 69 1. 930× 10 -3 5. 992× 10 -4 1. 98 1. 466× 10 -3 3. 722× 10 -4 6 / 12 points per half-width 3 / 6 points per half-width The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 27

Numerical results 3 D simulation of monopole point source in subsonic flow case (to assess the numerical tools used by partners) Mass source Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 28

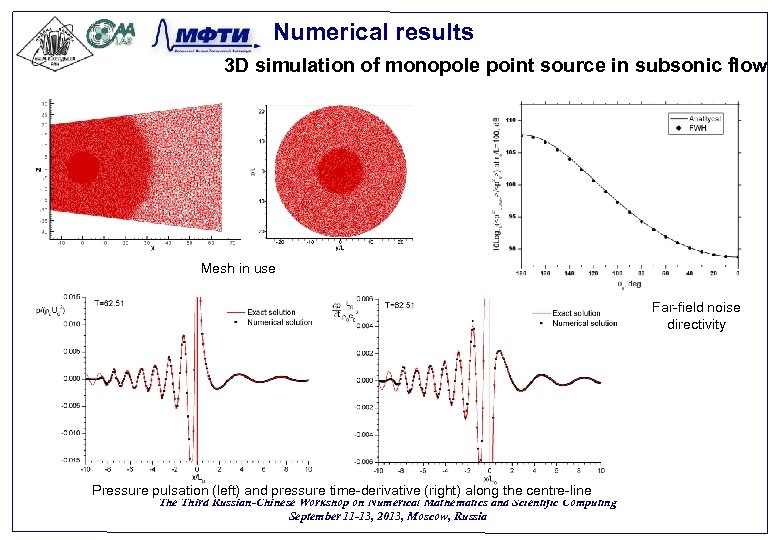
Numerical results 3 D simulation of monopole point source in subsonic flow Mesh in use Far-field noise directivity Pressure pulsation (left) and pressure time-derivative (right) along the centre-line Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 29

Intermediate concluding remarks EBR scheme can be considered as a FD quasi-1 D method In other words, they are closer to FD than to FV content If we adopt the quasi-1 D philosophy of scheme construction, a lot of useful further developments can be done Among them are: - quasi-1 D higher-accuracy scheme for cell-centered formulation - quasi-1 D shock capturing techniques (TVD, WENO) - quasi-1 D higher-accuracy scheme in polar/spherical coordinates for better treatment of curvilinear body shapes - quasi-1 D higher-accuracy scheme for unstructured meshes of arbitrary elements - quasi-1 D higher-accuracy scheme for turbulence closure models The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 30

WENO-EBR schemes The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 31

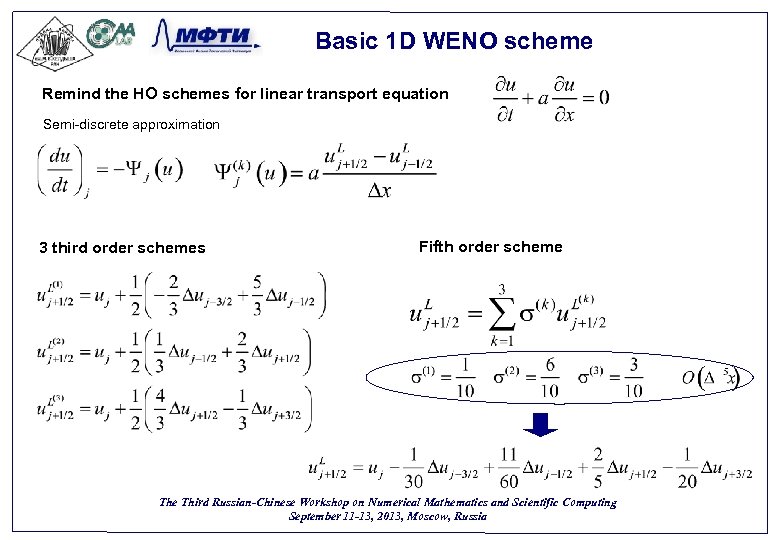
Basic 1 D WENO scheme Remind the HO schemes for linear transport equation Semi-discrete approximation 3 third order schemes Fifth order scheme Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 32

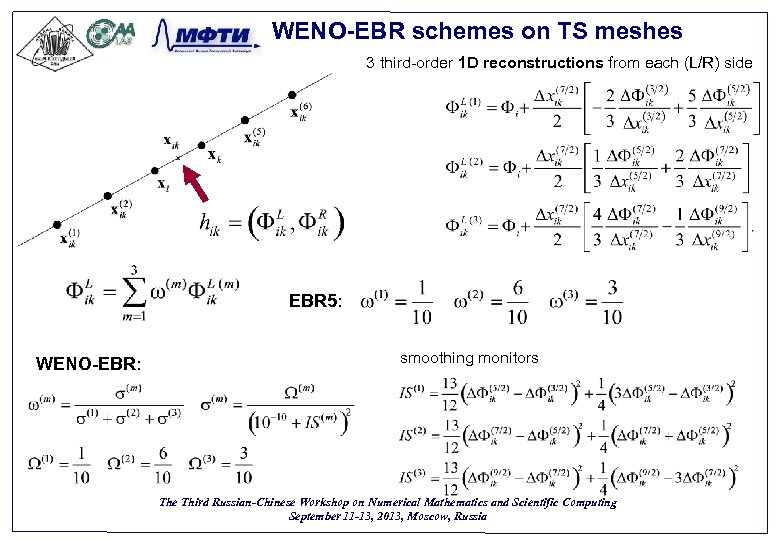
WENO-EBR schemes on TS meshes 3 third-order 1 D reconstructions from each (L/R) side EBR 5: WENO-EBR: smoothing monitors The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 33

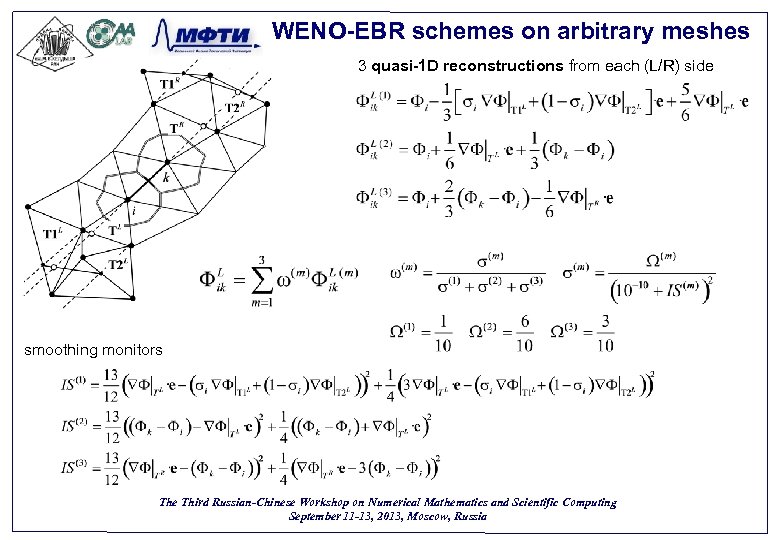
WENO-EBR schemes on arbitrary meshes 3 quasi-1 D reconstructions from each (L/R) side smoothing monitors The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 34

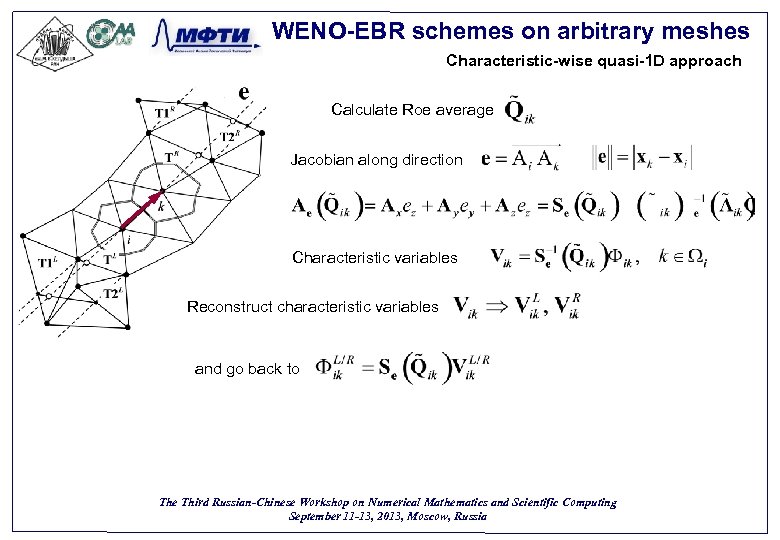
WENO-EBR schemes on arbitrary meshes Characteristic-wise quasi-1 D approach Calculate Roe average Jacobian along direction Characteristic variables Reconstruct characteristic variables and go back to The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 35

NOISEtte in-house code for solving aerodynamics and aeroacoustics problems on unstructured meshes ● 100 M tetras MPI, 8 Open. MP threads Euler based family of models EE, NSE, NLDE, LEE Non-inertial reference frame is available ● Turbulence modeling RANS, LES, DDES, IDDES ● Unstructured tetrahedral meshes ● Higher accuracy numerical scheme EBR multi-parameter vertex-centered scheme (up to 6 th order) Finite-element approach for diffusive terms WENO-EBR schemes for shock capturing ● Implicit and explicit time integration Explicit Runge-Kutta up to 4 -th order Implicit 2 -nd order Newton with preconditioned BICG-stab solver ● Far field acoustics FW/H method ● Boundary conditions at open boundaries Characteristic-based flux splitting, Tam non-reflecting, periodicity ● Hybrid two-level MPI+Open. MP parallelization Heterogeneous parallel model including GPU-Open. CL under development The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 36

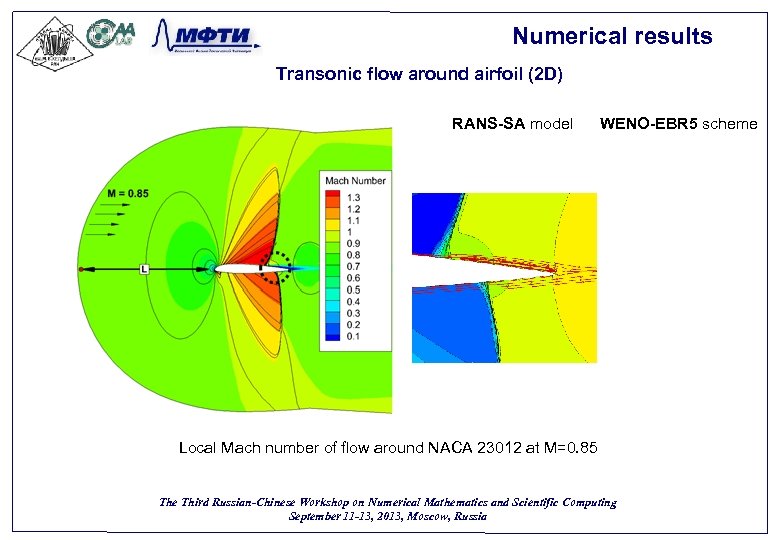
Numerical results Transonic flow around airfoil (2 D) RANS-SA model WENO-EBR 5 scheme Local Mach number of flow around NACA 23012 at M=0. 85 The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 37

Numerical results Transonic flow around airfoil (2 D) RANS-SA model WENO-EBR 5 scheme Local Mach number of flow around biconvex airfoil at M=0. 9: numerical results (top), Schlieren photography (bottom) The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 38

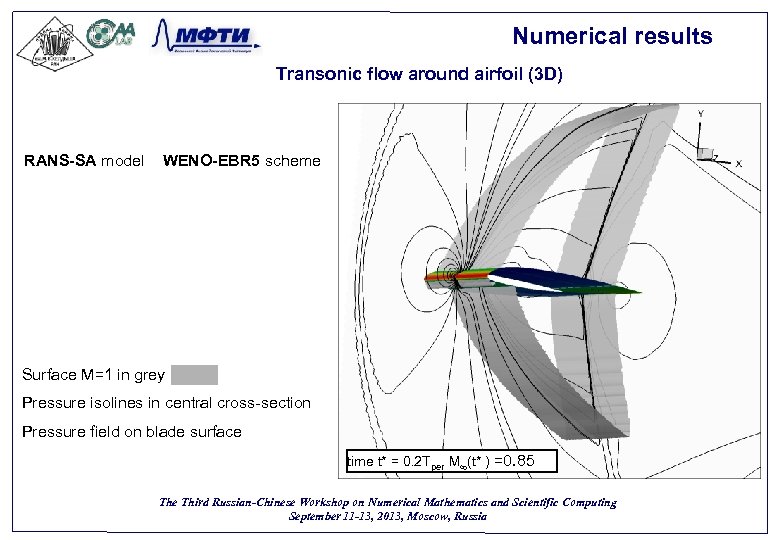
Numerical results Transonic flow around airfoil (3 D) RANS-SA model WENO-EBR 5 scheme Surface М=1 in grey Pressure isolines in central cross-section Pressure field on blade surface time t* = 0. 2 Tper M (t* ) =0. 85 The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 39

Numerical results Subsonic turbulent flow around helicopter blade IDDES hybrid model EBR 5 scheme Mesh ~ 700000 nodes ~ 4 M tetrahedrons 2 -criterion for vorticity visualization: Zero-isosurface of 2 nd Eigen value of tensor S 2+W 2 (S=(ui, j+uj, i)/2, W=(ui, j-uj, i)/2) The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 40

Numerical results Subsonic turbulent flow around helicopter blade IDDES hybrid model EBR 5 scheme Visualization of The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 41

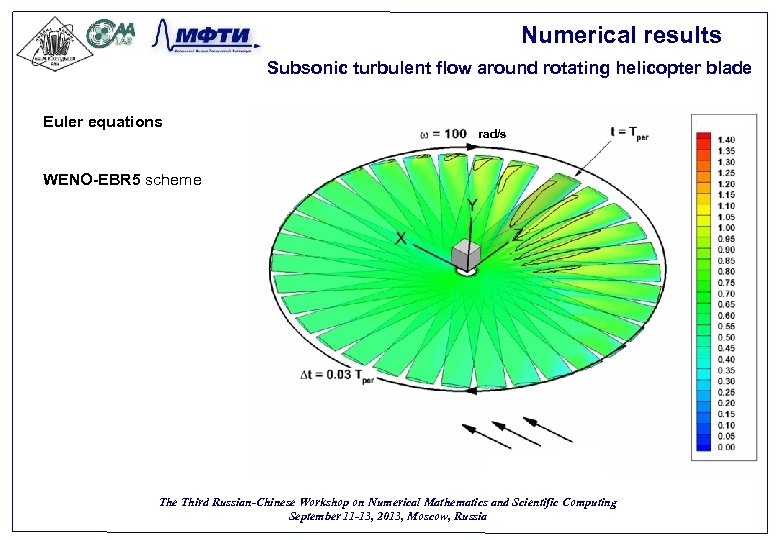
Numerical results Subsonic turbulent flow around rotating helicopter blade Euler equations rad/s WENO-EBR 5 scheme m/s The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 42

Numerical results Subsonic turbulent flow around cylinder Re=56000 (D=0. 012 [m], v=70 [m/s]) IDDES model EBR 6 scheme Implicit time integration of 2 nd order : Newton linearization, Bi. CGStab solver Far field: FFWH 192 MPI X 8 Open. MP (1536 cores) on Lomonosov supercomputer Computational set-up The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 43

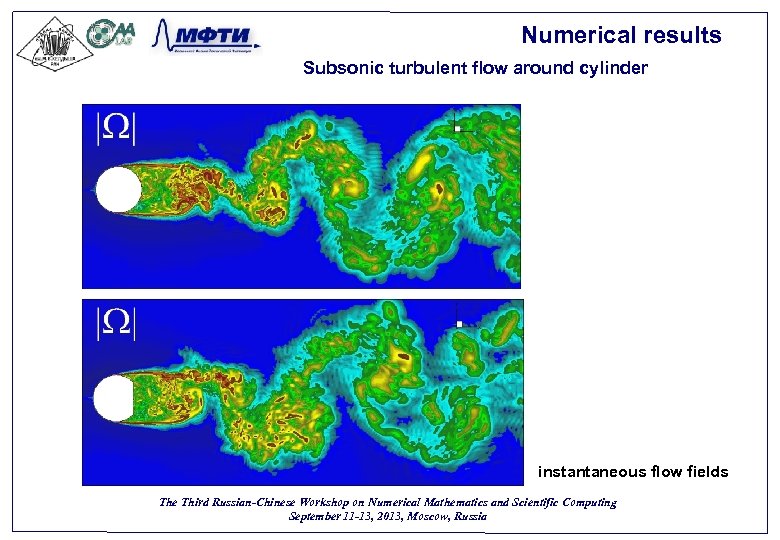
Numerical results Subsonic turbulent flow around cylinder instantaneous flow fields The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 44

Numerical results Subsonic turbulent flow around cylinder The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 45

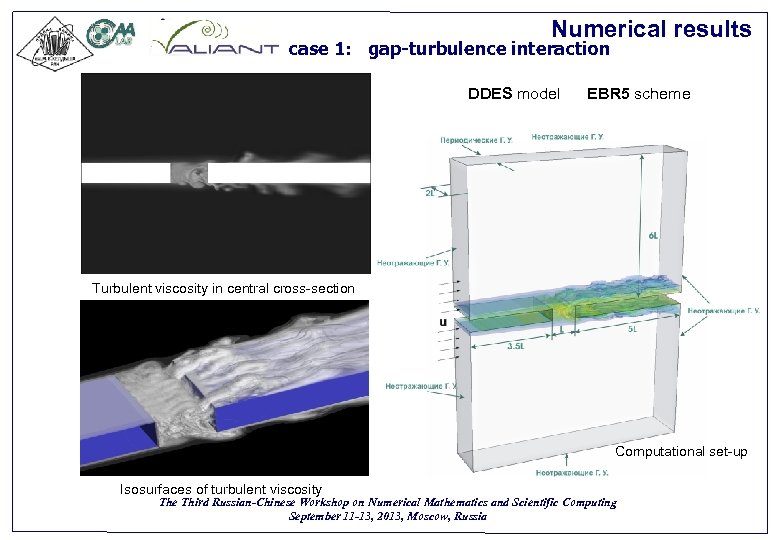
Numerical results case 1: gap-turbulence interaction DDES model EBR 5 scheme Вид сверху Turbulent viscosity in central cross-section Вид сбоку m/s Computational set-up Isosurfaces of turbulent viscosity The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 46

Numerical results Gap-turbulence interaction case Вид сверху Вид сбоку The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 47

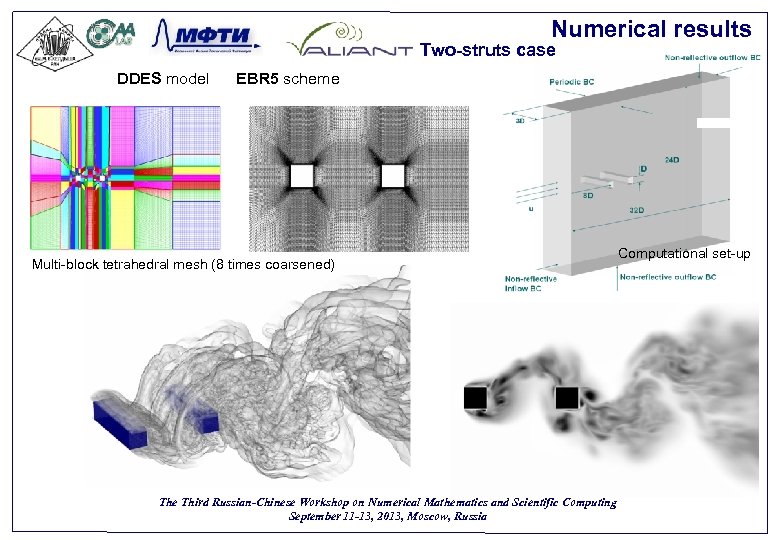
Numerical results Two-struts case DDES model EBR 5 scheme Computational set-up Multi-block tetrahedral mesh (8 times coarsened) Вид сбоку The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 48

case 4: two-struts Numerical results Вид сверху Вид сбоку The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 49

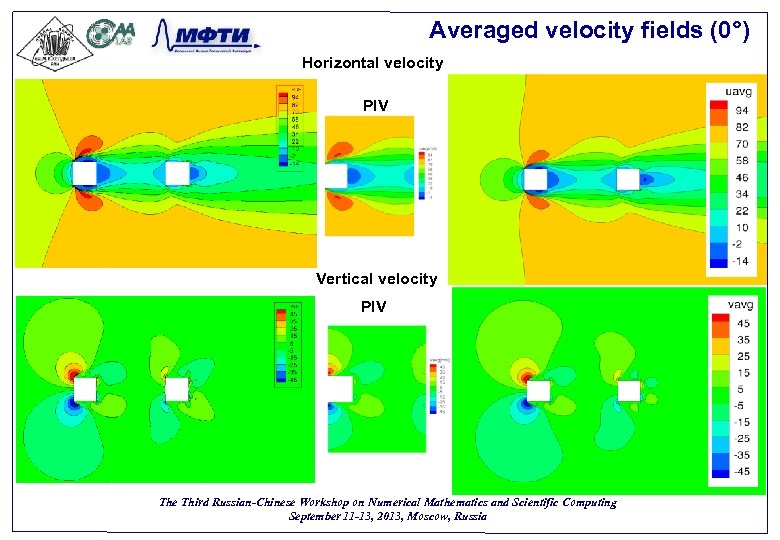
Averaged velocity fields (0°) Horizontal velocity PIV Vertical velocity PIV The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 50

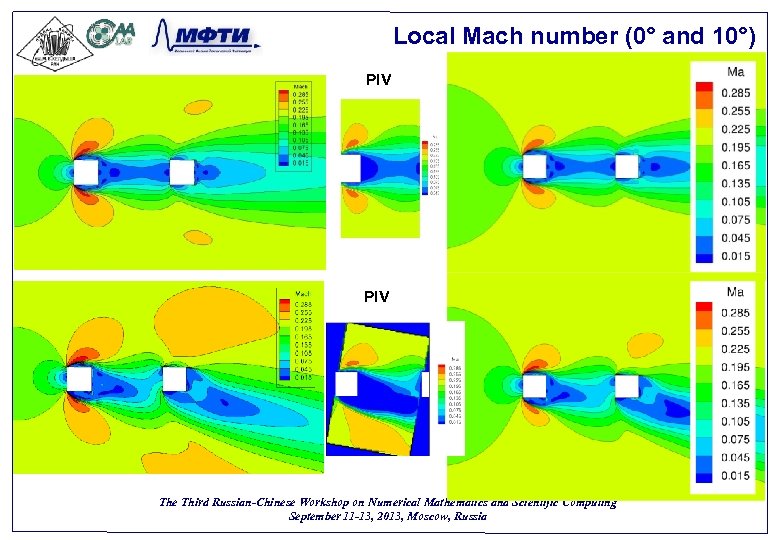
Local Mach number (0° and 10°) PIV The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 51

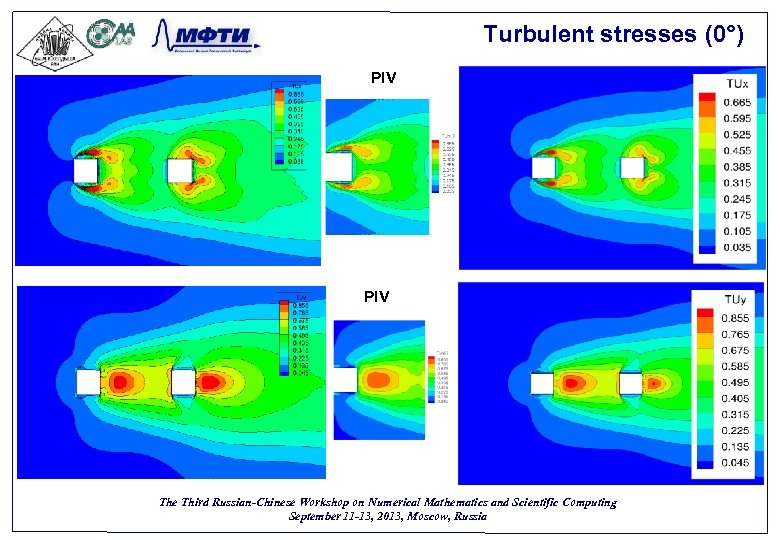
Turbulent stresses (0°) PIV The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 52

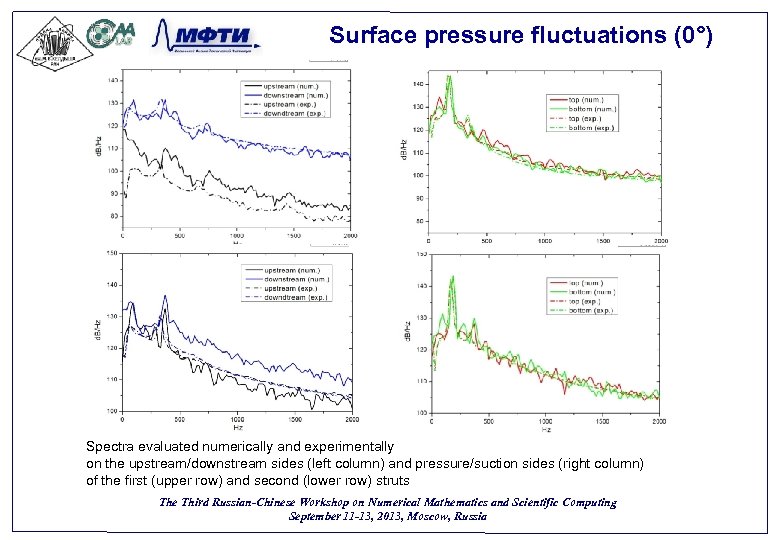
Surface pressure fluctuations (0°) Spectra evaluated numerically and experimentally on the upstream/downstream sides (left column) and pressure/suction sides (right column) of the first (upper row) and second (lower row) struts The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 53

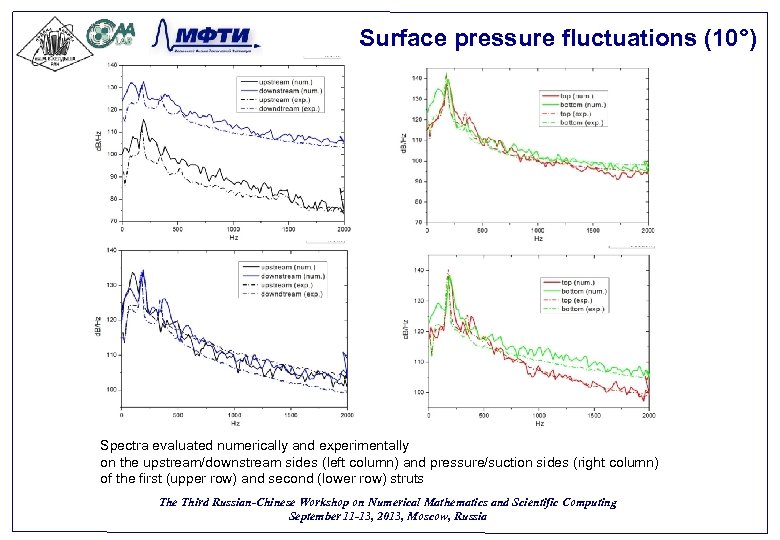
Surface pressure fluctuations (10°) Spectra evaluated numerically and experimentally on the upstream/downstream sides (left column) and pressure/suction sides (right column) of the first (upper row) and second (lower row) struts The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 54

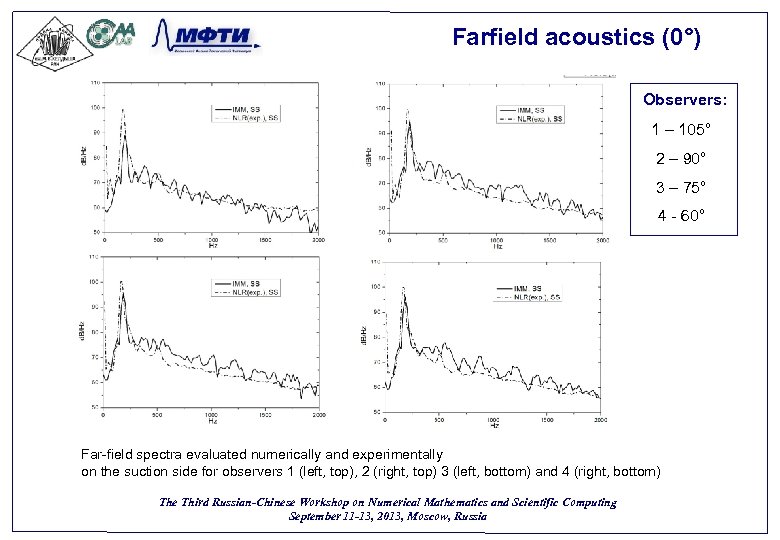
Farfield acoustics (0°) Observers: 1 – 105° 2 – 90° 3 – 75° 4 - 60° Far-field spectra evaluated numerically and experimentally on the suction side for observers 1 (left, top), 2 (right, top) 3 (left, bottom) and 4 (right, bottom) The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 55

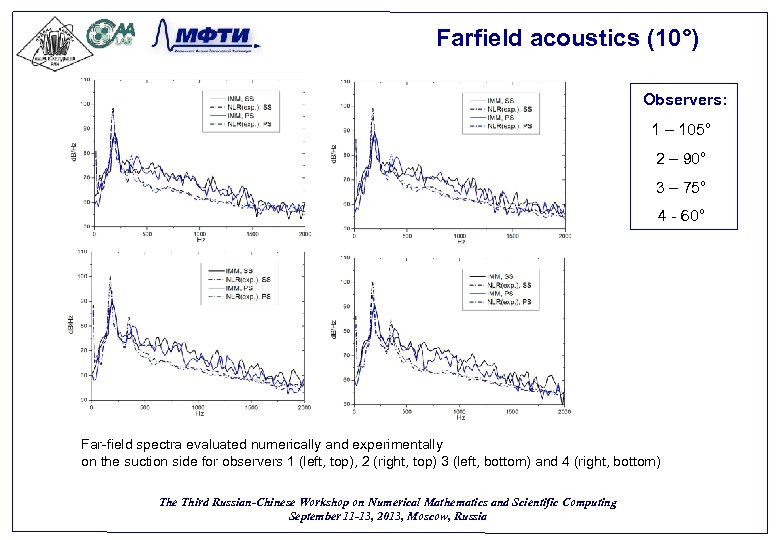
Farfield acoustics (10°) Observers: 1 – 105° 2 – 90° 3 – 75° 4 - 60° Far-field spectra evaluated numerically and experimentally on the suction side for observers 1 (left, top), 2 (right, top) 3 (left, bottom) and 4 (right, bottom) The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 56

case 4: two-struts turbulent viscosity entropy Numerical results vorticity magnitude Вид сверху Вид сбоку density The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 57

Concluding Remarks EBR schemes is a kind of FD scheme for unstructured meshes. EBR schemes possess high-order accuracy for a wide class of meshes, high. ER accuracy for arbitrary meshes used in practice EBR schemes can be considered as a good compromise between costs and accuracy providing low. ER costs and high. ER accuracy EBR schemes is an efficient numerical algorithm for applications The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 58

Acknowledgements Support: FP 7 VALIANT Project Government Contracts 14. 514. 12. 0003, 14. 514. 11. 4057 RFBR Projects 12 -01 -00486, 11 -01 -12096 -офи-м-2011, 12 -01 -33022 Computations: in-house code NOISEtte (Keldysh Institute of Applied Mathematics) supercomputers Lomonosov (Moscow State University), K 100 (Keldysh Institute of Applied Mathematics) The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 59

Thank you for attention! The Third Russian-Chinese Workshop on Numerical Mathematics and Scientific Computing September 11 -13, 2013, Moscow, Russia 60