ECON 4100 Industrial Organization Lecture 10 The Bertrand

ECON 4100: Industrial Organization Lecture 10 The Bertrand Model

Oligopoly Models • There are three dominant oligopoly models – Cournot – Bertrand – Stackelberg • Now we will consider the Bertrand Model

Price Competition: Bertrand • In the Cournot model price is set by some market clearing mechanism, firms seem relatively passive • An alternative approach is to assume that firms compete in Check that with prices: => Bertrand this demand • This leads to dramatically different resultsthese costs the • Take a simple example monopoly price is – two firms producing an identical product $30 and quantity – firms choose the prices at which they sell their water units is 40 – each firm has constant marginal cost of $10 – market demand is Q = 100 - 2 P

Bertrand competition (cont. ) • We need the derived demand for each firm – demand conditional upon the price charged by the other firm • Take Firm 2. Assume that Firm 1 has set a price of $25 – if Firm 2 sets a price greater than $25 she will sell nothing – if Firm 2 sets a price less than $25 she gets the whole market – if Firm 2 sets a price of exactly $25 consumers are indifferent between the two firms – the market is shared, presumably 50: 50 • So we have the derived demand for Firm 2 – q 2 = 0 – q 2 = 100 - 2 p 2 – q 2 = 0. 5(100 - 50) = 25 if p 2 > p 1 = $25 if p 2 < p 1 = $25 if p 2 = p 1 = $25

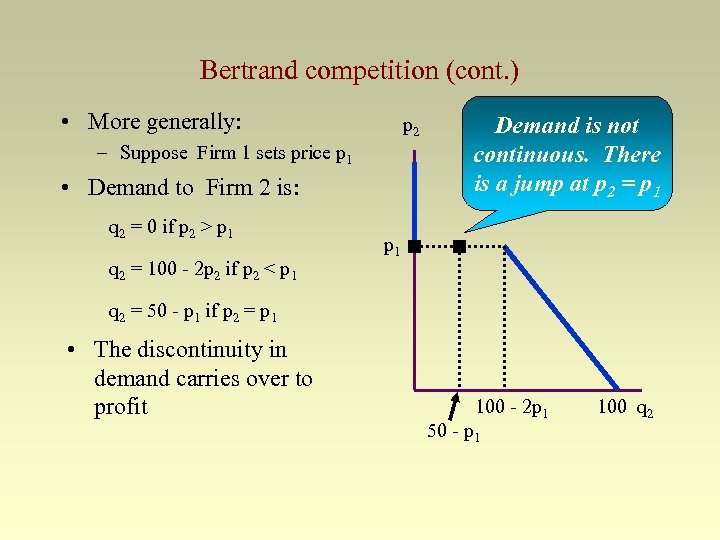
Bertrand competition (cont. ) • More generally: p 2 – Suppose Firm 1 sets price p 1 • Demand to Firm 2 is: q 2 = 0 if p 2 > p 1 q 2 = 100 - 2 p 2 if p 2 < p 1 Demand is not continuous. There is a jump at p 2 = p 1 q 2 = 50 - p 1 if p 2 = p 1 • The discontinuity in demand carries over to profit 100 - 2 p 1 50 - p 1 100 q 2

Bertrand competition (cont. ) Firm 2’s profit is: p 2(p 1, , p 2) = 0 if p 2 > p 1 p 2(p 1, , p 2) = (p 2 - 10)(100 - 2 p 2) if p 2 < p 1 p 2(p 1, , p 2) = (p 2 - 10)(50 - p 2) if p 2 = p 1 Clearly this depends on p 1. For whatever reason! Suppose first that Firm 1 sets a “very high” price: greater than the monopoly price of $30

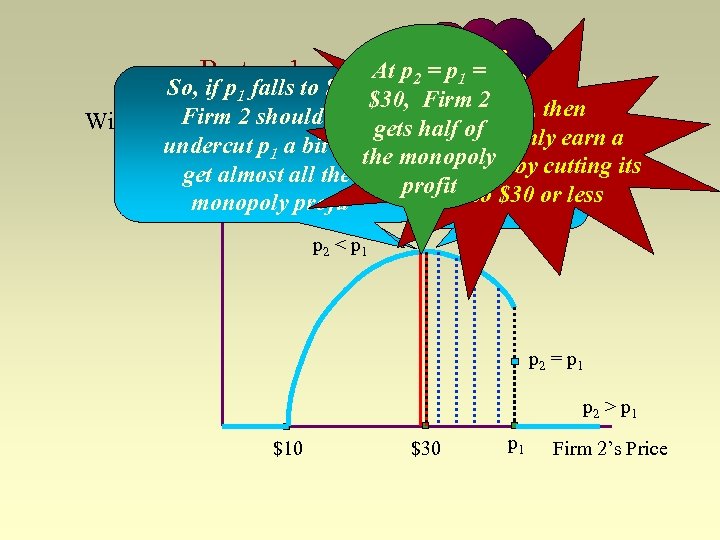
What price At p 2 = p. Firm 2 Bertrand competition (cont. ) should 1 = So, if p 1 falls to $30, Firm 2 If p set? Firm 2 should profit looks like=this: then just gets half 1 $30, With p 1 > $30, Firm 2’s Firm 2 of only earn a will undercut p 1 a bit and monopoly What if the 1 Firm 2’s Profit all Firm positive profit by cutting its The monopoly get almost pricesprofit at $30? profit to $30$30 less price of or monopoly p 2 < p 1 p 2 = p 1 p 2 > p 1 $10 $30 p 1 Firm 2’s Price

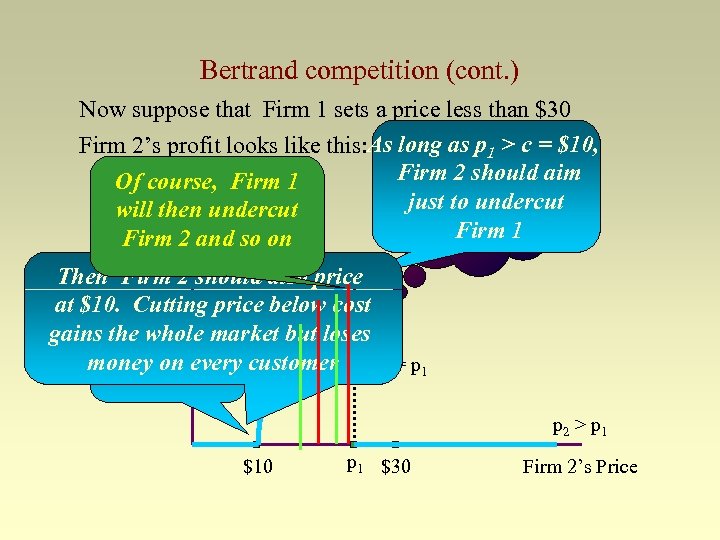
Bertrand competition (cont. ) Now suppose that Firm 1 sets a price less than $30 Firm 2’s profit looks like this: As long as p 1 > c = $10, Firm 2 should aim What price Of course, Firm 1 Firm 2’s Profit just to Firm 2 should undercut will then undercut set Firm 1 now? Firm 2 and so on p <p 2 1 Then Firm 2 should also price at $10. Cutting price below cost gains the whole market but loses What if Firm 1 money on $10? customer p 2 = p 1 prices at every p 2 > p 1 $10 p 1 $30 Firm 2’s Price

Bertrand competition (cont. ) • We now have Firm 2’s best response to any price set by Firm 1: – p*2 = $30 – p*2 = p 1 - “something small” – p*2 = $10 if p 1 > $30 if $10 < p 1 < $30 if p 1 < $10 • We have a symmetric best response for Firm 1 – p*1 = $30 – p*1 = p 2 - “something small” – p*1 = $10 if p 2 > $30 if $10 < p 2 < $30 if p 2 < $10

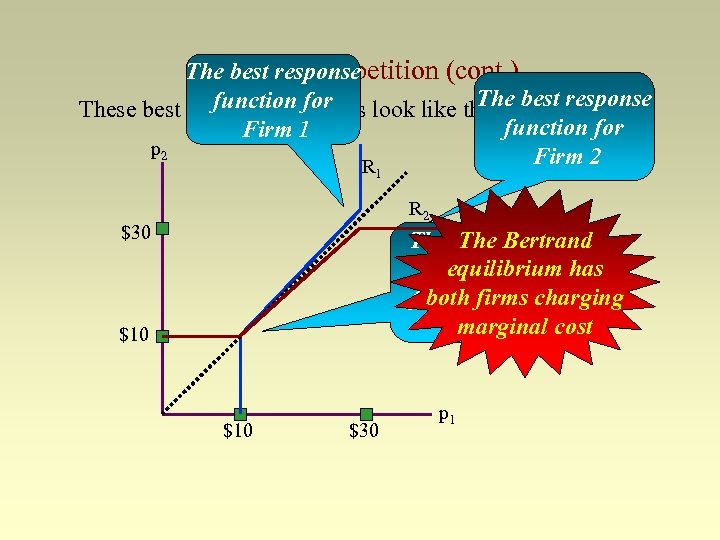
The best response Bertrand competition (cont. ) The function for These best response functions look like this best response function for Firm 1 p 2 Firm 2 R 1 R 2 $30 The Bertrand The equilibrium isequilibrium has with both firms charging firms pricing at marginal cost $10 $10 $30 p 1

Bertrand Equilibrium: modifications • Bertrand: competition in prices is very different from competition in quantities • Since many firms seem to set prices (and not quantities) this is a challenge to the Cournot approach • But the Bertrand model has problems too – for the p = marginal-cost equilibrium to arise, both firms need enough capacity to fill all demand at price = MC – but when both firms set p = c they each get only half the market – So, at the p = marginal cost equilibrium, there is huge excess capacity • This calls attention to the choice of capacity – Note: choosing capacity is a lot like choosing output which brings us back to the Cournot model • The intensity of price competition when products are identical that the Bertrand model reveals also gives a motivation for Product differentiation

An Example of Product Differentiation Coke and Pepsi are nearly identical but not quite. As a result, the lowest priced product does not win the entire market. QC = 63. 42 - 3. 98 PC + 2. 25 PP MCC = $4. 96 QP = 49. 52 - 5. 48 PP + 1. 40 PC MCP = $3. 96 There at least two methods for solving this for PC and PP

Bertrand Product Differentiation Method 1: Calculus Profit of Coke: p. C = (PC - 4. 96)(63. 42 - 3. 98 PC + 2. 25 PP) Profit of Pepsi: p. P = (PP - 3. 96)(49. 52 - 5. 48 PP + 1. 40 PC) Differentiate with respect to PC and PP respectively Method 2: MR = MC Reorganize the demand functions PC = (15. 93 + 0. 57 PP) - 0. 25 QC PP = (9. 04 + 0. 26 PC) - 0. 18 QP Calculate marginal revenue, equate to marginal cost, solve for QC and QP and substitute in the demand functions

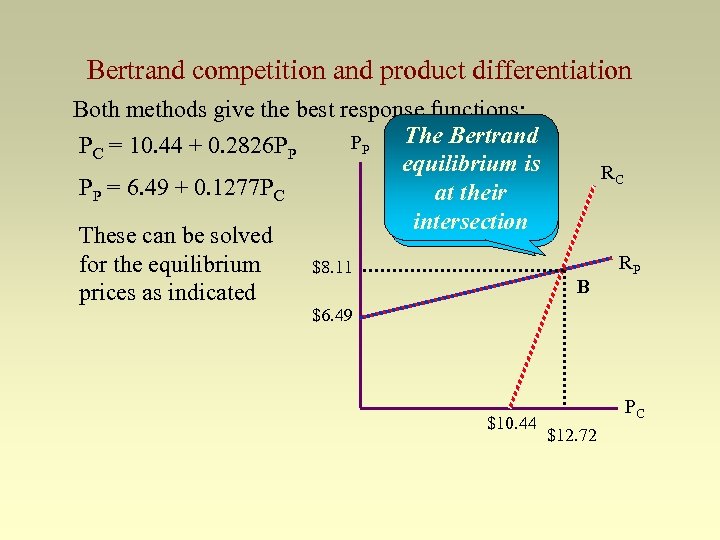
Bertrand competition and product differentiation Both methods give the best response functions: The Bertrand PP PC = 10. 44 + 0. 2826 PP Note that these equilibrium is PP = 6. 49 + 0. 1277 PC are upward at their sloping intersection These can be solved for the equilibrium $8. 11 prices as indicated RC B RP $6. 49 $10. 44 PC $12. 72

Bertrand Competition and the Spatial Model • An alternative approach is to use the spatial model from Chapter 4 – – a Main Street over which consumers are distributed supplied by two shops located at opposite ends of the street but now the shops are competitors each consumer buys exactly one unit of the good provided that its full price is less than V – a consumer buys from the shop offering the lower full price – consumers incur transport costs of t per unit distance in travelling to a shop • What prices will the two shops charge?

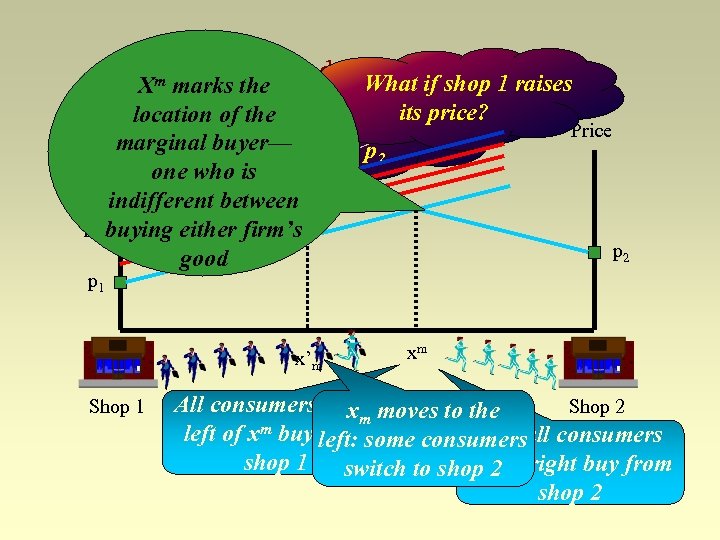
Xm Bertrand the spatial model What if shop 1 raises marks the Assume that shop 1 sets location of the p and shopits sets price 1 2 price? Price marginal buyer— price p 2 one who is indifferent between p’ 1 buying either firm’s good Price p 2 p 1 x’m Shop 1 xm All consumers to x moves to the Shop 2 m left of xm buy left: some consumersall consumers from And shop 1 switch to shop 2 right buy from to the shop 2

$Bertrand This spatial model the is the fraction of consumers who p 1 +$

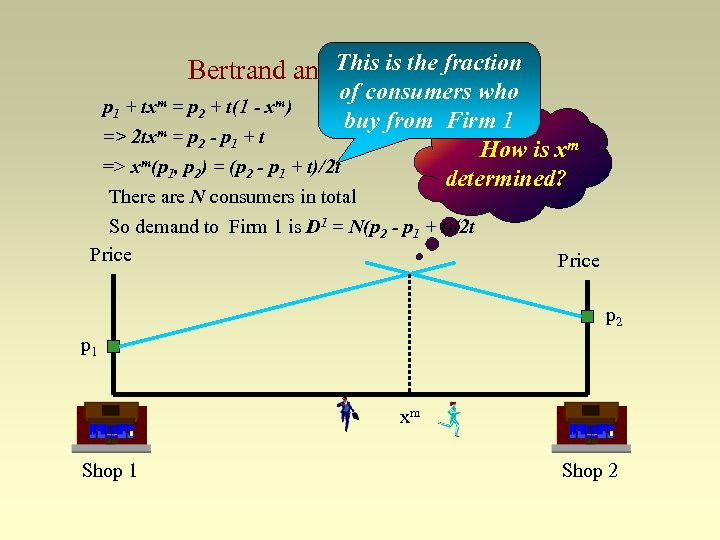
Bertrand This spatial model the is the fraction of consumers who p 1 + = p 2 + t(1 buy from Firm 1 m=p -p +t => 2 tx 2 1 How is xm => xm(p 1, p 2) = (p 2 - p 1 + t)/2 t determined? txm xm) There are N consumers in total So demand to Firm 1 is D 1 = N(p 2 - p 1 + t)/2 t Price p 2 p 1 xm Shop 1 Shop 2

Bertrand equilibrium Profit to Firm 1 is p 1 = (p 1 - c)D 1 = N(p 1 - c)(p 2 - p 1 + t)/2 t p 1 = N(p 2 p 1 - p 12 + tp 1 + cp 1 - cp 2 -ct)/2 t Solve this This is for p 1 Differentiate with respect to pthe best 1 response function N for Firm 1 p 1/ p 1 = (p 2 - 2 p 1 + t + c) = 0 2 t p*1 = (p 2 + t + c)/2 This is the best response function for Firm What about Firm 2? By symmetry, it has a 2 similar best response function. p*2 = (p 1 + t + c)/2

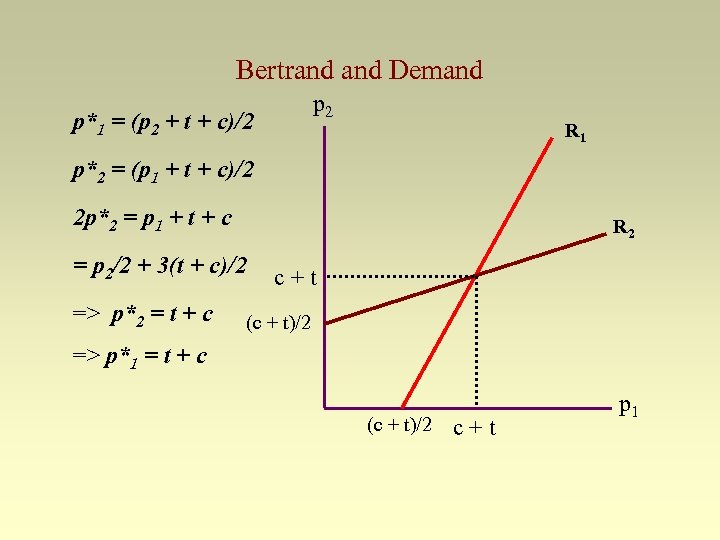
Bertrand Demand p 2 p*1 = (p 2 + t + c)/2 R 1 p*2 = (p 1 + t + c)/2 2 p*2 = p 1 + t + c R 2 = p 2/2 + 3(t + c)/2 => p*2 = t + c c+t (c + t)/2 => p*1 = t + c (c + t)/2 c+t p 1

Next: Stackelberg • Firms choose outputs sequentially – leader sets output first, and visibly – follower then sets output • The firm moving first has a leadership advantage – can anticipate the follower’s actions – can therefore manipulate the follower