ECE 667 Spring 2013 Synthesis and Verification of

ECE 667 Spring 2013 Synthesis and Verification of Digital Systems Boolean Functions SOP Representation Slides adopted (with permission) from A. Kuehlmann, UC Berkeley 2003 1

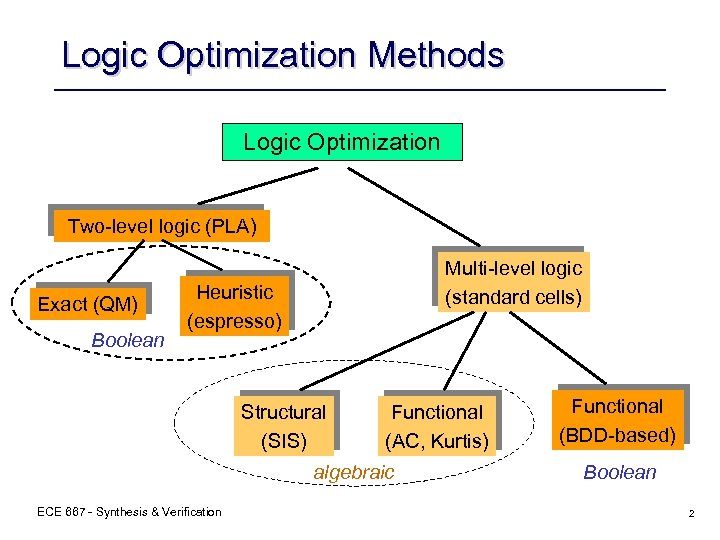Logic Optimization Methods Logic Optimization Two-level logic (PLA) Exact (QM) Boolean Multi-level logic (standard cells) Heuristic (espresso) Structural (SIS) Functional (AC, Kurtis) algebraic ECE 667 - Synthesis & Verification Functional (BDD-based) Boolean 2

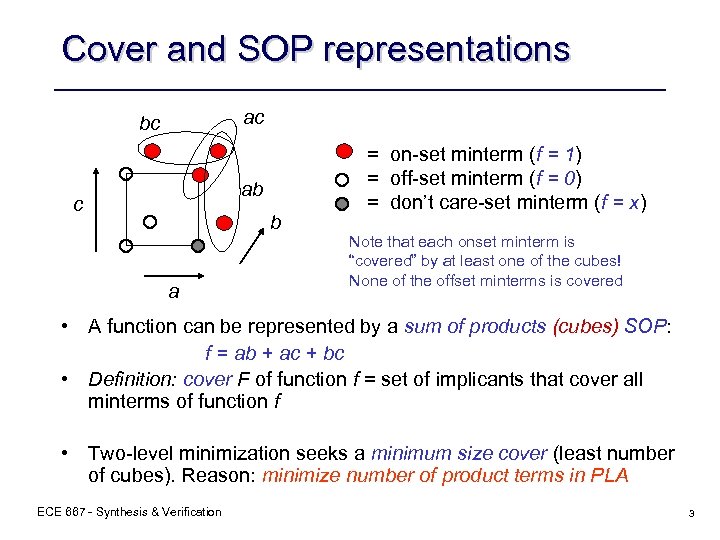Cover and SOP representations ac bc ab c b a = on-set minterm (f = 1) = off-set minterm (f = 0) = don’t care-set minterm (f = x) Note that each onset minterm is “covered” by at least one of the cubes! None of the offset minterms is covered • A function can be represented by a sum of products (cubes) SOP: f = ab + ac + bc • Definition: cover F of function f = set of implicants that cover all minterms of function f • Two-level minimization seeks a minimum size cover (least number of cubes). Reason: minimize number of product terms in PLA ECE 667 - Synthesis & Verification 3

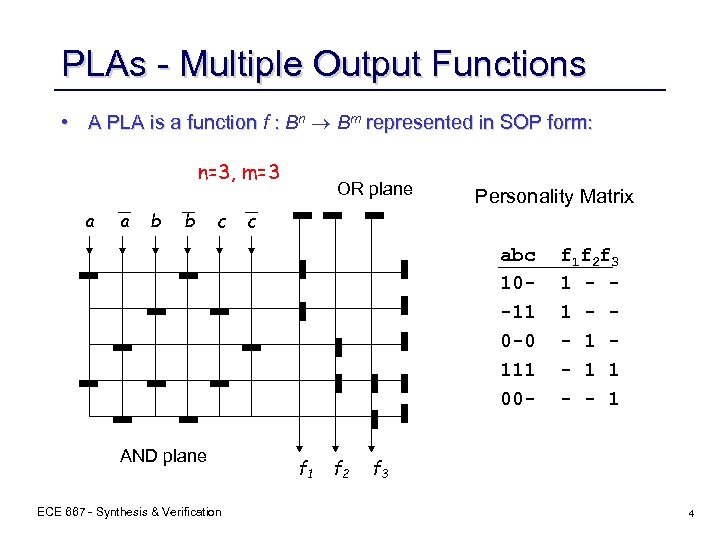PLAs - Multiple Output Functions • A PLA is a function f : Bn Bm represented in SOP form: n=3, m=3 a a b b c OR plane c Personality Matrix abc 10 -11 0 -0 111 00 - AND plane ECE 667 - Synthesis & Verification f 1 f 2 f 1 f 2 f 3 1 - - 1 f 3 4

PLAs (cont. ) • Each distinct cube appears just once in the AND-plane, and can be shared by (multiple) outputs in the OR-plane, e. g. , cube abc. • Extensions from single output to multiple output minimization theory are straightforward. • Multi-level logic can be viewed mathematically as a collection of single output functions. ECE 667 - Synthesis & Verification 5

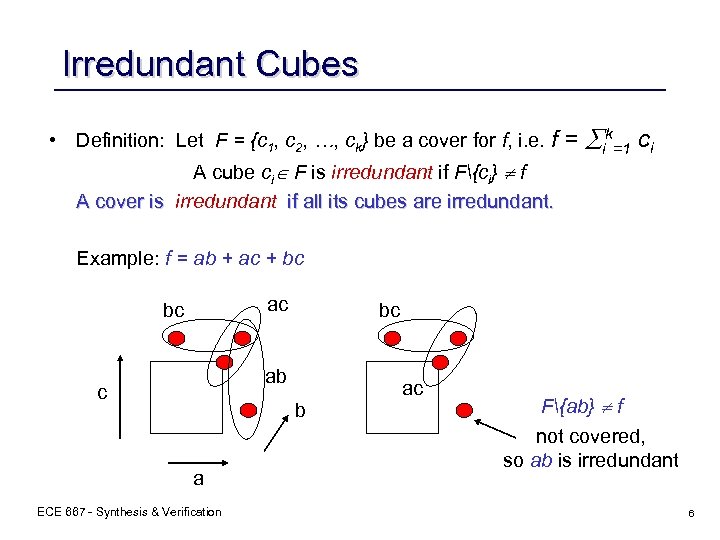Irredundant Cubes • Definition: Let F = {c 1, c 2, …, ck} be a cover for f, i. e. f = ik=1 ci A cube ci F is irredundant if F{ci} f A cover is irredundant if all its cubes are irredundant. Example: f = ab + ac + bc ac bc bc ab c b a ECE 667 - Synthesis & Verification ac F{ab} f not covered, so ab is irredundant 6

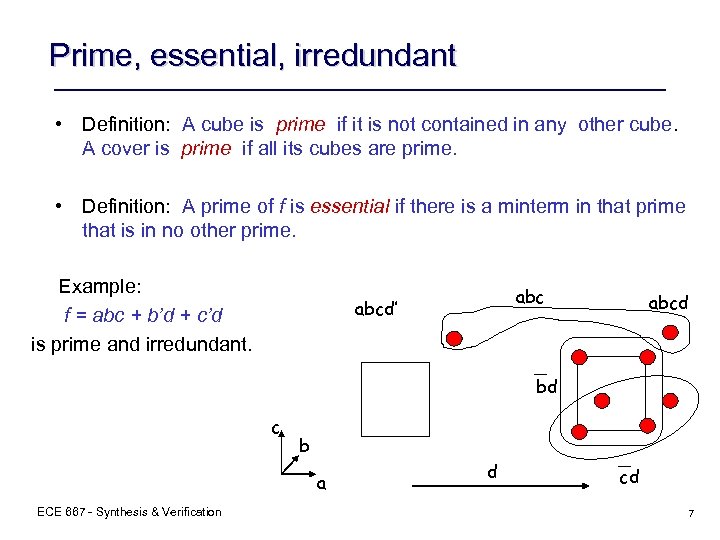Prime, essential, irredundant • Definition: A cube is prime if it is not contained in any other cube. A cover is prime if all its cubes are prime. • Definition: A prime of f is essential if there is a minterm in that prime that is in no other prime. Example: f = abc + b’d + c’d is prime and irredundant. abcd’ abcd bd c b a ECE 667 - Synthesis & Verification d cd 7

Prime Cubes – another definition • A literal j of cube ci F ( cover of f ) is prime if (F {ci }) {c”i } f where c”i is ci with literal j of ci deleted. • A cube of F is prime if all its literals are prime. F=ac + bc + a = F {ci } {c”i } Example f = ab + ac + bc ci = ab; c”i = a (literal b deleted) F {ci } {c”i } = a + ac + bc c Not equal to f since offset vertex is covered ECE 667 - Synthesis & Verification bc ac a b a 8

Orthogonal cubes • Definition: Two cubes are orthogonal if they do not have any minterm in common – Example: c 1= ab c 2 = b’c are orthogonal c 1= ab’ c 2 = b’c are not orthogonal c 1= ab’ c 2 = ab are ? ECE 667 - Synthesis & Verification 9

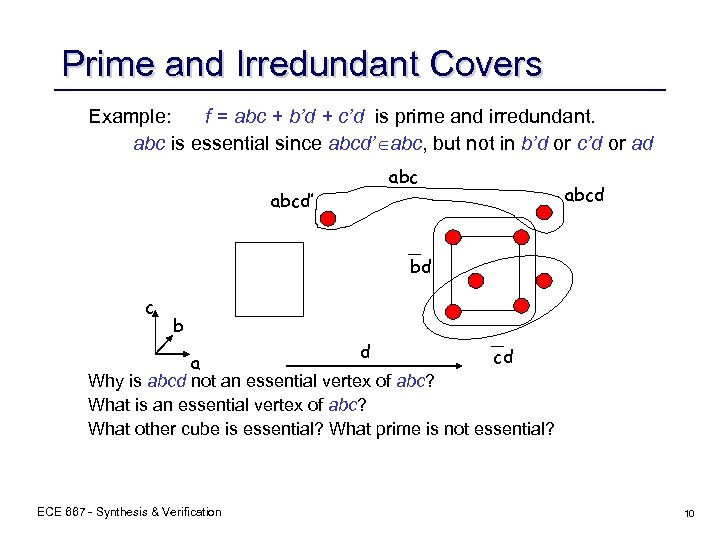Prime and Irredundant Covers Example: f = abc + b’d + c’d is prime and irredundant. abc is essential since abcd’ abc, but not in b’d or c’d or ad abcd’ abcd bd c b d cd a Why is abcd not an essential vertex of abc? What is an essential vertex of abc? What other cube is essential? What prime is not essential? ECE 667 - Synthesis & Verification 10

Quine’s Theorem Importance of having prime cubes: • minimum SOP solution can be composed of prime cubes only Theorem (Quine): There exists a minimum cover that is prime • Given initial cover for F = (f, d, r), find a minimum cover G of primes where: f G f+d G is a prime cover of F ; f = on-set, r = off-set, d = don’t care set ECE 667 - Synthesis & Verification 11

Shannon (Boole) Cofactors Let f : Bn B be a Boolean function, and x= (x 1, x 2, …, xn) the variables in the support of f. The cofactor fa of f w. r. t literal a=xi or a=x’i is: fxi (x 1, x 2, …, xn) = f (x 1, …, xi-1, 1, xi+1, …, xn) fx’i (x 1, x 2, …, xn) = f (x 1, …, xi-1, 0, xi+1, …, xn) The computation of the cofactor is a fundamental operation in Boolean reasoning ! Example: f = abc + abc fa = bc c c b a ECE 667 - Synthesis & Verification b a 12

Generalized Cofactor • The generalized cofactor f. C of f by a cube C is f with the fixed values indicated by the literals of C, e. g. if C=xi x’j, then xi =1, and xj =0. • if C= x 1 x’ 4 x 6 f. C is just the function f restricted to the subspace where x 1 =x 6 =1 and x 4 =0. • As a function, f. C does not depend on x 1, x 4 or x 6 anymore (However, we still consider f. C as a function of all n variables, it just happens to be independent of x 1, x 4 and x 6). • x 1 f fx 1 Example: f = ac + a’c , af = ac, fa=c ECE 667 - Synthesis & Verification 13

Cofactor of Covers Definition: The cofactor of a cover F is the sum of the cofactors of each of the cubes of F. Note: If F={c 1, c 2, …, ck} is a cover of f, then Fc= {(c 1)c, (c 2)c, …, (ck)c} is a cover of fc. Suppose F(x) is a cover of f(x), i. e. Then for 1 j n, is a cover of fxj(x) ECE 667 - Synthesis & Verification 14

Cofactor of Cubes Definition: The cofactor Cxj of a cube C with respect to a literal xj is • C if xj and x’j do not appear in C • C{xj} if xj appears positively in C, i. e. xj C • if xj appears negatively in C, i. e. xj’ C Example 1: C = x 1 x’ 4 x 6 Cx 2 = C (x 2 and x’ 2 do not appear in C ) Cx 1 = x’ 4 x 6 (x 1 appears positively in C) Cx 4 = (x 4 appears negatively in C) Example 2: F = abc + b’d + c’d Fb = ac + c’d (Just drop b everywhere and delete cubes containing literal b) ECE 667 - Synthesis & Verification 15

Fundamental Theorem: Let c be a cube and f a function. Then c f fc 1. Proof. We use the fact that x fx = x f, and fx is independent of x. If : Suppose fc 1. Then cf =fcc = c. Thus, c f. f c ECE 667 - Synthesis & Verification 16

Proof (cont. ) Only if. Assume c f Then c cf = cfc. But fc is independent of literals i c. If fc 1, then m Bn, fc(m)=0. We will construct a m’ from m and c in the following manner: mi’=mi, if xi c and xi c, mi’=1, if xi c, mi’=0, if xi c. i. e. , we made the literals of m’ agree with c, i. e. m’ c Þ c(m’)=1 Also, fc is independent of literals xi, xi c Þ fc(m’) = fc(m) = 0 C=xz Þ fc(m’)= 0 contradicting c cfc. m= 000 m’= 101 m ECE 667 - Synthesis & Verification m’ 17

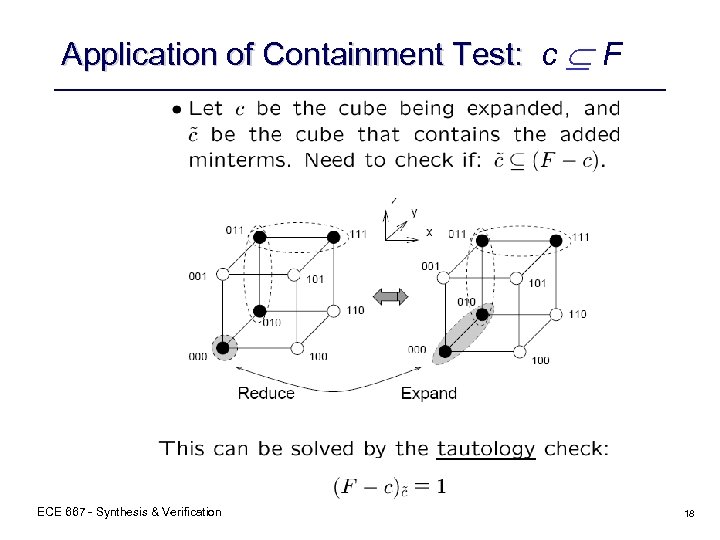Application of Containment Test: c F ECE 667 - Synthesis & Verification 18

Shannon Expansion f : Bn B Shannon Expansion: Theorem: F is a cover of f. Then We say that f (F) is expanded about xi. xi is called the splitting variable. ECE 667 - Synthesis & Verification 19

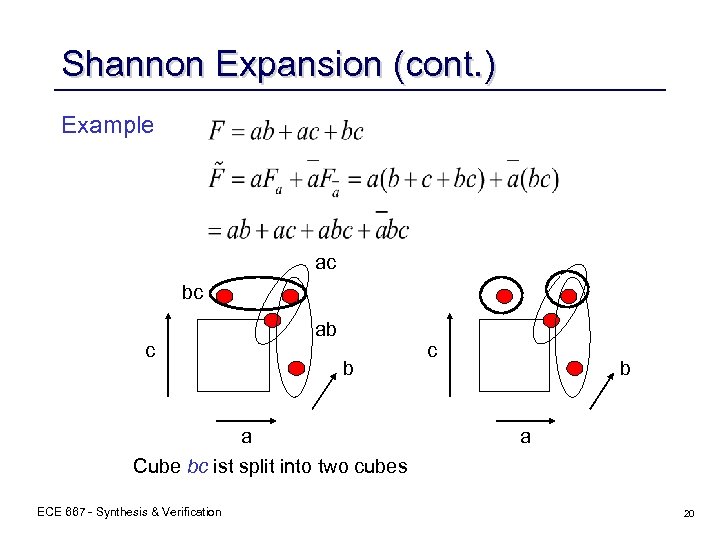Shannon Expansion (cont. ) Example ac bc c ab b a Cube bc ist split into two cubes ECE 667 - Synthesis & Verification c b a 20