071277340242760f8d79df197a0b2789.ppt
- Количество слайдов: 32
 ECE-200 Week #4 http: //vle. dcollege. net Dr. Timothy P. Kurzweg 603 Commonwealth 215 -895 -0549 kurzweg@ece. drexel. edu Office Hours: Tuesdays 4: 00 -6: 00 or by appointment Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
ECE-200 Week #4 http: //vle. dcollege. net Dr. Timothy P. Kurzweg 603 Commonwealth 215 -895 -0549 kurzweg@ece. drexel. edu Office Hours: Tuesdays 4: 00 -6: 00 or by appointment Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Announcements • HW #3 Due Wednesday April 25 th IN CLASS • Lab #1 due in recitation this week: April 26/27 • TAs are available for help with HW and Labs Mr. Vasileios Nasis 502 Bossone Building 215 -895 -1378 vasleios@ece. drexel. edu Office Hours: M 1 -3 Mr. Travis Doll 406 Bossone Building tmd 47@drexel. edu Office Hours: T 10 -12 Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Announcements • HW #3 Due Wednesday April 25 th IN CLASS • Lab #1 due in recitation this week: April 26/27 • TAs are available for help with HW and Labs Mr. Vasileios Nasis 502 Bossone Building 215 -895 -1378 vasleios@ece. drexel. edu Office Hours: M 1 -3 Mr. Travis Doll 406 Bossone Building tmd 47@drexel. edu Office Hours: T 10 -12 Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
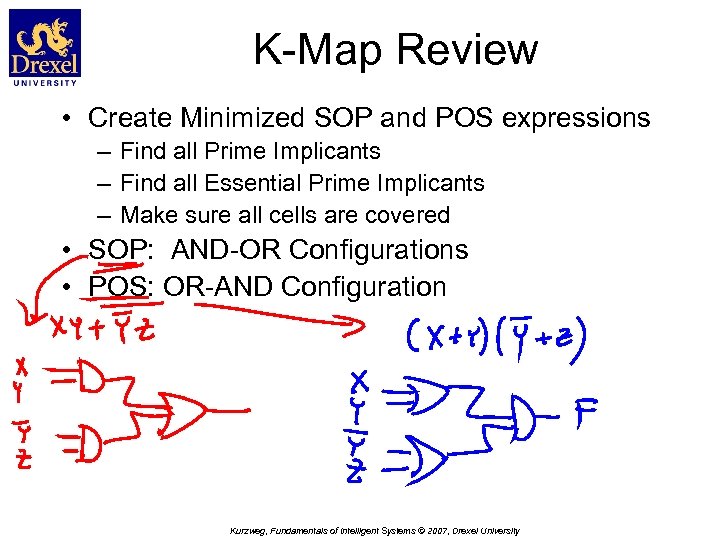 K-Map Review • Create Minimized SOP and POS expressions – Find all Prime Implicants – Find all Essential Prime Implicants – Make sure all cells are covered • SOP: AND-OR Configurations • POS: OR-AND Configuration Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
K-Map Review • Create Minimized SOP and POS expressions – Find all Prime Implicants – Find all Essential Prime Implicants – Make sure all cells are covered • SOP: AND-OR Configurations • POS: OR-AND Configuration Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Circuits using NAND/NOR Gates • NAND and NOR gates are: – Typically faster – Typically smaller • Therefore, a common design goal is to use NAND and NOR gates. • How do we change the: – SOP (AND/OR Configuration) and the – POS (OR/AND Configuration) into NAND/NOR Configurations Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Circuits using NAND/NOR Gates • NAND and NOR gates are: – Typically faster – Typically smaller • Therefore, a common design goal is to use NAND and NOR gates. • How do we change the: – SOP (AND/OR Configuration) and the – POS (OR/AND Configuration) into NAND/NOR Configurations Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
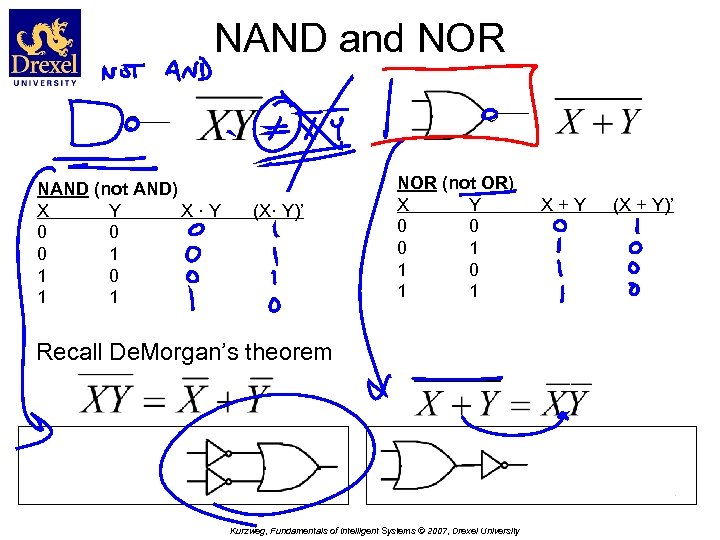 NAND and NOR NAND (not AND) X Y X·Y 0 0 0 1 1 (X· Y)’ NOR (not OR) X Y 0 0 0 1 1 Recall De. Morgan’s theorem Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University X+Y (X + Y)’
NAND and NOR NAND (not AND) X Y X·Y 0 0 0 1 1 (X· Y)’ NOR (not OR) X Y 0 0 0 1 1 Recall De. Morgan’s theorem Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University X+Y (X + Y)’
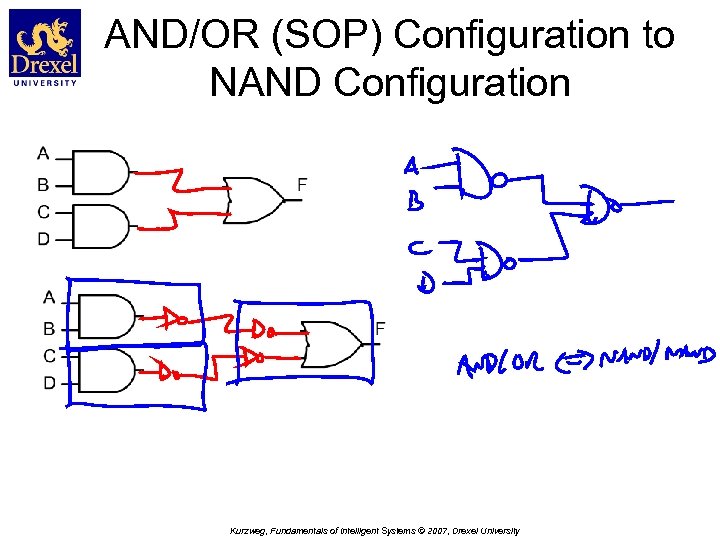 AND/OR (SOP) Configuration to NAND Configuration Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
AND/OR (SOP) Configuration to NAND Configuration Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
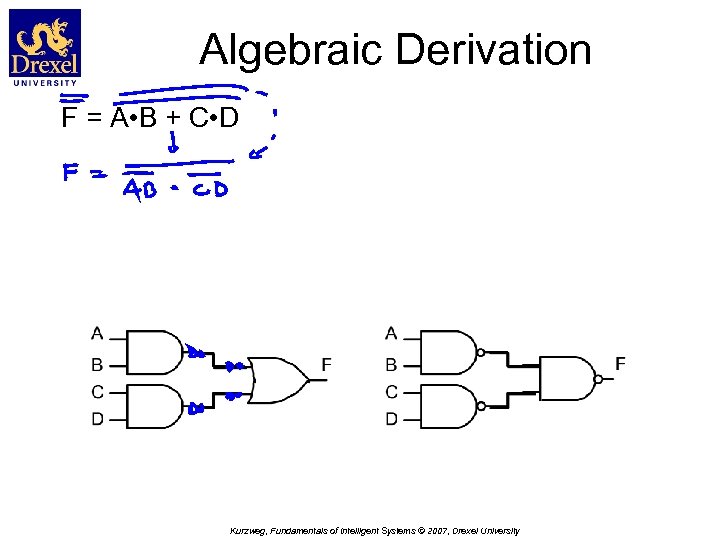 Algebraic Derivation F = A • B + C • D Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Algebraic Derivation F = A • B + C • D Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
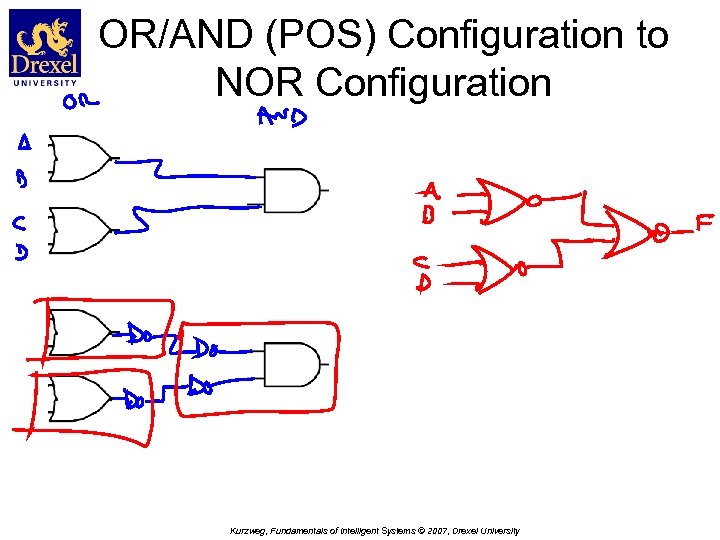 OR/AND (POS) Configuration to NOR Configuration Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
OR/AND (POS) Configuration to NOR Configuration Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Algebraic Derivation • F = (A+B) (C+D) Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Algebraic Derivation • F = (A+B) (C+D) Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
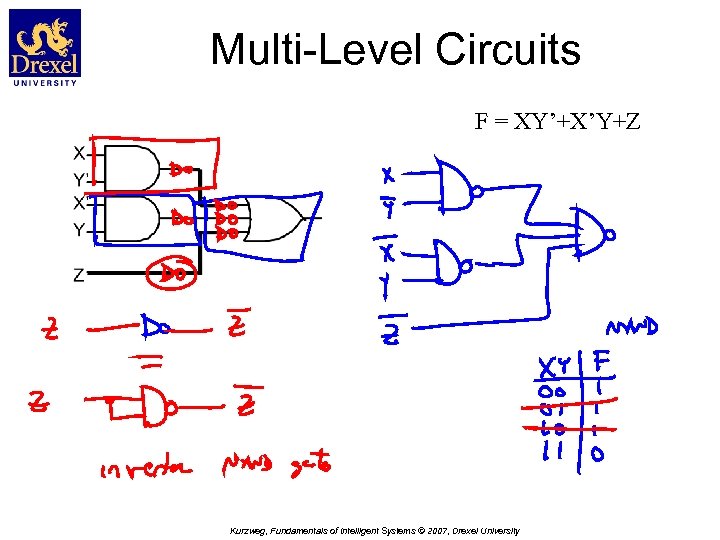 Multi-Level Circuits F = XY’+X’Y+Z Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Multi-Level Circuits F = XY’+X’Y+Z Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
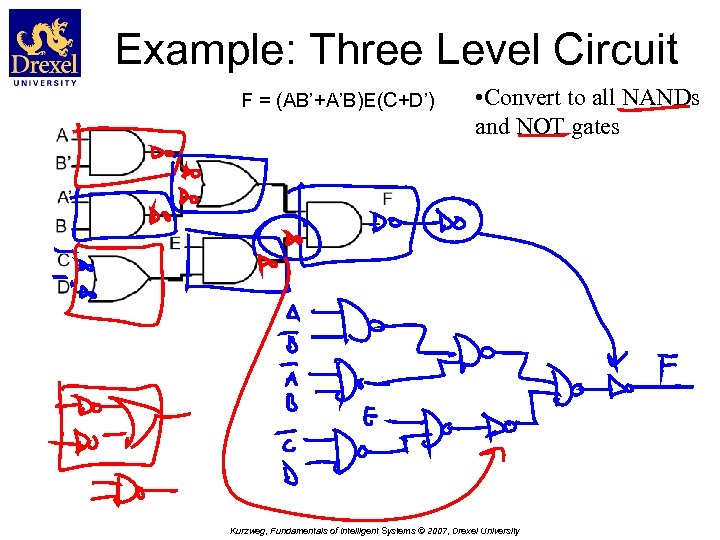 Example: Three Level Circuit F = (AB’+A’B)E(C+D’) • Convert to all NANDs and NOT gates Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Example: Three Level Circuit F = (AB’+A’B)E(C+D’) • Convert to all NANDs and NOT gates Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Combinational Logic Design • Goal (ie, why are we doing this? ) – Want to express functions, F(W, X, Y, Z), in hardware (circuits) • How – Take what we have learned to describe functions (minterms and maxterms) and minimize these (algebraic or K-maps) – Use building blocks (ie, electrical chips) to implement minimized functions • AND, OR, NAND, Inverters, PLA, Decoders, Encoders, MUX……. . Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Combinational Logic Design • Goal (ie, why are we doing this? ) – Want to express functions, F(W, X, Y, Z), in hardware (circuits) • How – Take what we have learned to describe functions (minterms and maxterms) and minimize these (algebraic or K-maps) – Use building blocks (ie, electrical chips) to implement minimized functions • AND, OR, NAND, Inverters, PLA, Decoders, Encoders, MUX……. . Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Integrated Circuit (IC) Technology IC Integration Types: Number of gates on a chip has grown • SSI: Small Scale Integration – < 10 gates • MSI: Medium Scale Integration – 10 to 100 gates • LSI: Large Scale Integration – 100 to few 1000 s • VLSI: Very Large Scale Integration – Several 1000 s to tens of 1, 000 • Software has been key to advancement of digital systems! Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Integrated Circuit (IC) Technology IC Integration Types: Number of gates on a chip has grown • SSI: Small Scale Integration – < 10 gates • MSI: Medium Scale Integration – 10 to 100 gates • LSI: Large Scale Integration – 100 to few 1000 s • VLSI: Very Large Scale Integration – Several 1000 s to tens of 1, 000 • Software has been key to advancement of digital systems! Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Design Procedure • Specification: Write a specification of the circuit • Formulation: Truth Table or Boolean Expression • Optimization: 2 -level and multiple-level optimization • Technology mapping: Use existing technology to implement the circuit • Verification: Verify the correctness of the design Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Design Procedure • Specification: Write a specification of the circuit • Formulation: Truth Table or Boolean Expression • Optimization: 2 -level and multiple-level optimization • Technology mapping: Use existing technology to implement the circuit • Verification: Verify the correctness of the design Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Design Trade-offs • • Input/Output delay Size or area of the chip Power dissipation Cost Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Design Trade-offs • • Input/Output delay Size or area of the chip Power dissipation Cost Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 What Description is Best? • What is the starting point of a design? – Word description – Truth table – Logic expression • No single best method. • Specificiation often comes in natural language (English). • Natural language is ambiguous, but easy to translate into logic. • Truth tables are unambigous, but bulky – 10 variables = 1024 rows Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
What Description is Best? • What is the starting point of a design? – Word description – Truth table – Logic expression • No single best method. • Specificiation often comes in natural language (English). • Natural language is ambiguous, but easy to translate into logic. • Truth tables are unambigous, but bulky – 10 variables = 1024 rows Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
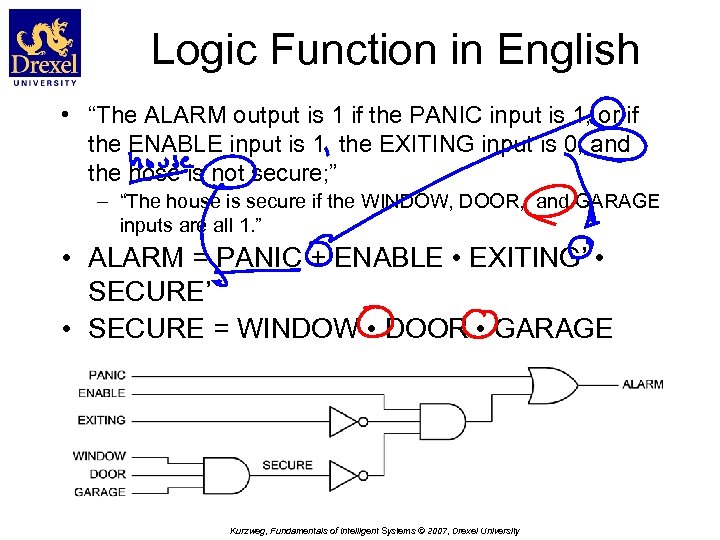 Logic Function in English • “The ALARM output is 1 if the PANIC input is 1, or if the ENABLE input is 1, the EXITING input is 0, and the hose is not secure; ” – “The house is secure if the WINDOW, DOOR, and GARAGE inputs are all 1. ” • ALARM = PANIC + ENABLE • EXITING’ • SECURE = WINDOW • DOOR • GARAGE Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Logic Function in English • “The ALARM output is 1 if the PANIC input is 1, or if the ENABLE input is 1, the EXITING input is 0, and the hose is not secure; ” – “The house is secure if the WINDOW, DOOR, and GARAGE inputs are all 1. ” • ALARM = PANIC + ENABLE • EXITING’ • SECURE = WINDOW • DOOR • GARAGE Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
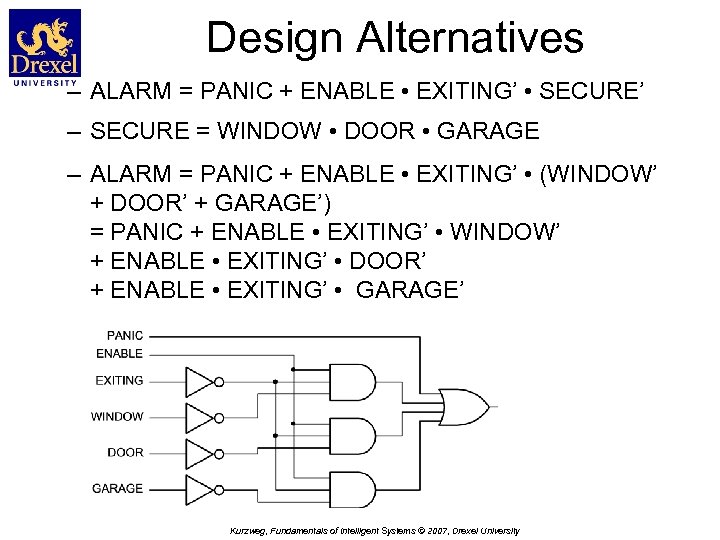 Design Alternatives – ALARM = PANIC + ENABLE • EXITING’ • SECURE’ – SECURE = WINDOW • DOOR • GARAGE – ALARM = PANIC + ENABLE • EXITING’ • (WINDOW’ + DOOR’ + GARAGE’) = PANIC + ENABLE • EXITING’ • WINDOW’ + ENABLE • EXITING’ • DOOR’ + ENABLE • EXITING’ • GARAGE’ Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Design Alternatives – ALARM = PANIC + ENABLE • EXITING’ • SECURE’ – SECURE = WINDOW • DOOR • GARAGE – ALARM = PANIC + ENABLE • EXITING’ • (WINDOW’ + DOOR’ + GARAGE’) = PANIC + ENABLE • EXITING’ • WINDOW’ + ENABLE • EXITING’ • DOOR’ + ENABLE • EXITING’ • GARAGE’ Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
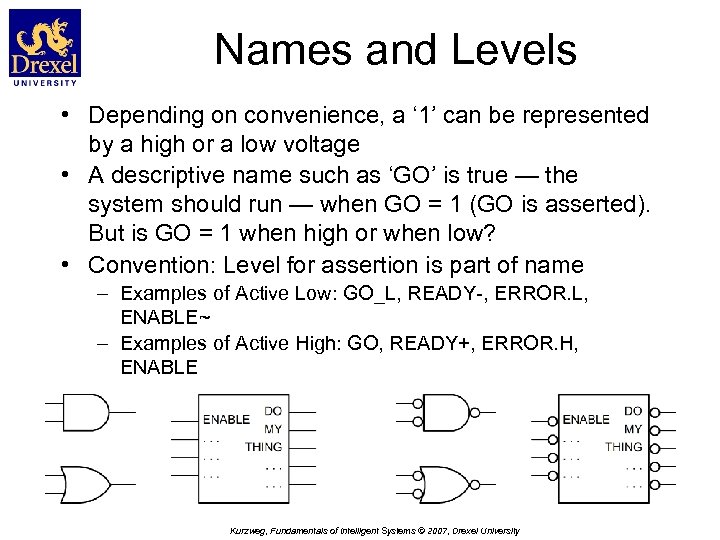 Names and Levels • Depending on convenience, a ‘ 1’ can be represented by a high or a low voltage • A descriptive name such as ‘GO’ is true — the system should run — when GO = 1 (GO is asserted). But is GO = 1 when high or when low? • Convention: Level for assertion is part of name – Examples of Active Low: GO_L, READY-, ERROR. L, ENABLE~ – Examples of Active High: GO, READY+, ERROR. H, ENABLE Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Names and Levels • Depending on convenience, a ‘ 1’ can be represented by a high or a low voltage • A descriptive name such as ‘GO’ is true — the system should run — when GO = 1 (GO is asserted). But is GO = 1 when high or when low? • Convention: Level for assertion is part of name – Examples of Active Low: GO_L, READY-, ERROR. L, ENABLE~ – Examples of Active High: GO, READY+, ERROR. H, ENABLE Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Announcements • • HW #3 Due Wednesday April 25 th IN CLASS Lab #1 due in recitation this week: April 26/27 TAs are available for help with HW and Labs Midterm Wednesday, May 2 IN CLASS – – Practice Midterm on-line this week Solutions placed on-line next Monday Exam is Closed Book, Closed Notes No electronic devices allowed (calculators, PDAs, cell phones, etc) – No Make-up Exams will be given without prior discussion with Dr. Kurzweg (at least 2 days in advance) Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Announcements • • HW #3 Due Wednesday April 25 th IN CLASS Lab #1 due in recitation this week: April 26/27 TAs are available for help with HW and Labs Midterm Wednesday, May 2 IN CLASS – – Practice Midterm on-line this week Solutions placed on-line next Monday Exam is Closed Book, Closed Notes No electronic devices allowed (calculators, PDAs, cell phones, etc) – No Make-up Exams will be given without prior discussion with Dr. Kurzweg (at least 2 days in advance) Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Word Problems – Combinational Design • A “majority function” circuit has three inputs (X, Y, and Z) and one output, F. Each input has a value of 1 or 0. For this circuit, the output F will take the value of the majority of the inputs. For example, if the inputs XYZ = 101, the output F will be 1 since the majority of the inputs are 1. Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Word Problems – Combinational Design • A “majority function” circuit has three inputs (X, Y, and Z) and one output, F. Each input has a value of 1 or 0. For this circuit, the output F will take the value of the majority of the inputs. For example, if the inputs XYZ = 101, the output F will be 1 since the majority of the inputs are 1. Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
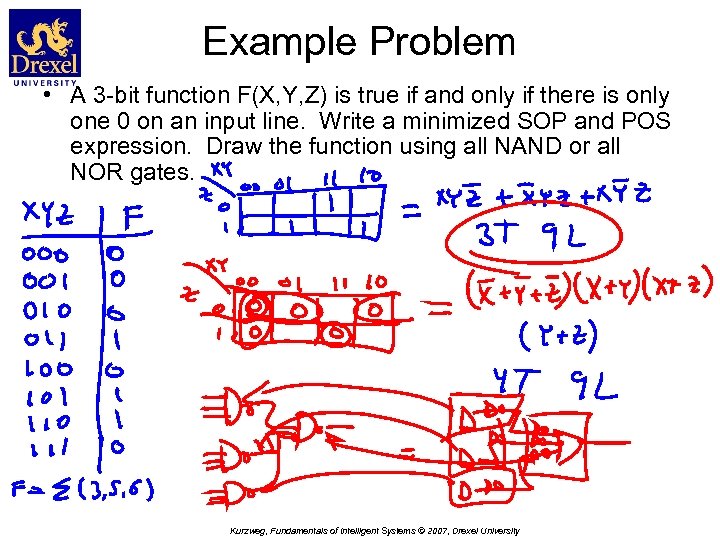 Example Problem • A 3 -bit function F(X, Y, Z) is true if and only if there is only one 0 on an input line. Write a minimized SOP and POS expression. Draw the function using all NAND or all NOR gates. Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Example Problem • A 3 -bit function F(X, Y, Z) is true if and only if there is only one 0 on an input line. Write a minimized SOP and POS expression. Draw the function using all NAND or all NOR gates. Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
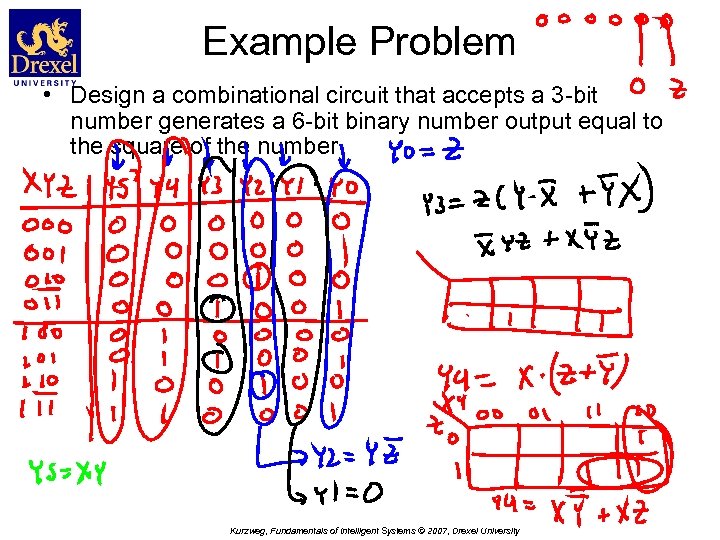 Example Problem • Design a combinational circuit that accepts a 3 -bit number generates a 6 -bit binary number output equal to the square of the number Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Example Problem • Design a combinational circuit that accepts a 3 -bit number generates a 6 -bit binary number output equal to the square of the number Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
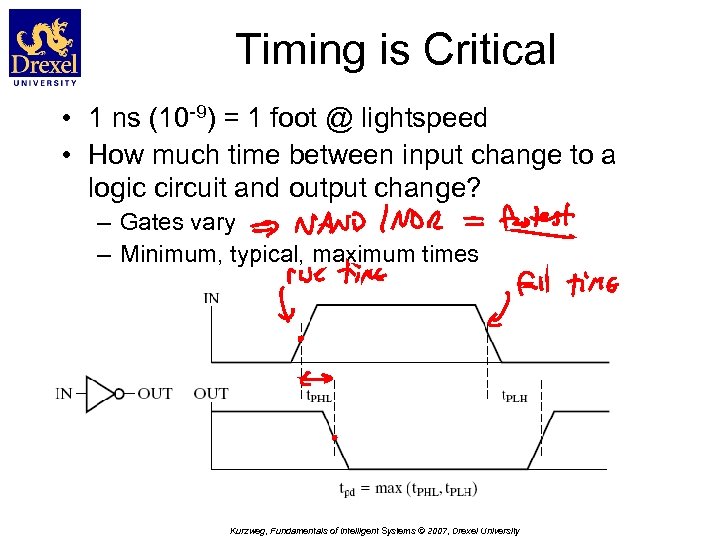 Timing is Critical • 1 ns (10 -9) = 1 foot @ lightspeed • How much time between input change to a logic circuit and output change? – Gates vary – Minimum, typical, maximum times Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Timing is Critical • 1 ns (10 -9) = 1 foot @ lightspeed • How much time between input change to a logic circuit and output change? – Gates vary – Minimum, typical, maximum times Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Source of Timing Info • Specification Sheets • Times for different devices are different • Part 74 x 00, NAND gate • Family 74 HCT 11 nsec typical, 35 nsec maximum • Family 74 AHCT 5. 5 nsec typical, 9 nsec maximum • Family 74 LS 9 -10 nsec typical, 15 nsec maximum • Accurate timing analysis is time consuming • Software tools available • Times depend on input patterns – Must be specified by designer Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Source of Timing Info • Specification Sheets • Times for different devices are different • Part 74 x 00, NAND gate • Family 74 HCT 11 nsec typical, 35 nsec maximum • Family 74 AHCT 5. 5 nsec typical, 9 nsec maximum • Family 74 LS 9 -10 nsec typical, 15 nsec maximum • Accurate timing analysis is time consuming • Software tools available • Times depend on input patterns – Must be specified by designer Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
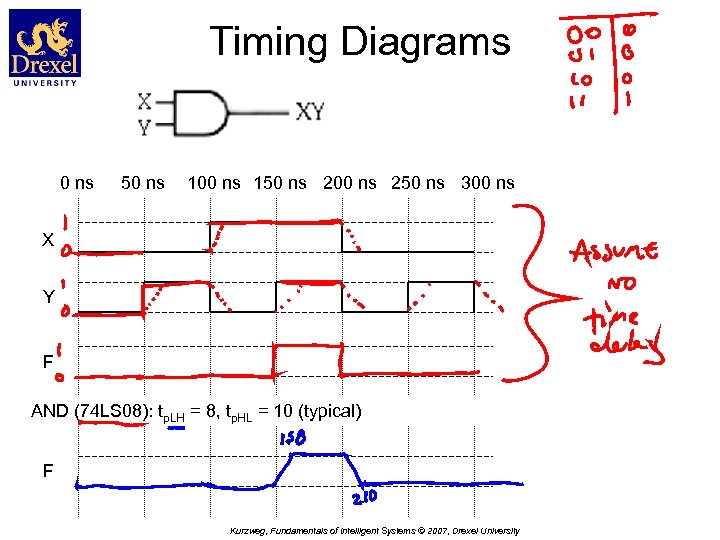 Timing Diagrams 0 ns 50 ns 100 ns 150 ns 200 ns 250 ns 300 ns X Y F AND (74 LS 08): tp. LH = 8, tp. HL = 10 (typical) F Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Timing Diagrams 0 ns 50 ns 100 ns 150 ns 200 ns 250 ns 300 ns X Y F AND (74 LS 08): tp. LH = 8, tp. HL = 10 (typical) F Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Combinational Circuits • Introduce “functional blocks” for circuit construction • Combinational Circuits take into account only the present state of the inputs and determines output – Sequential Circuits take into account the past states as well • Discuss: – – – Programmable Logic Arrays (PLA) Decoders Encoders Multiplexers Demultiplexers Tri-State Buffers Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Combinational Circuits • Introduce “functional blocks” for circuit construction • Combinational Circuits take into account only the present state of the inputs and determines output – Sequential Circuits take into account the past states as well • Discuss: – – – Programmable Logic Arrays (PLA) Decoders Encoders Multiplexers Demultiplexers Tri-State Buffers Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Programmable Logic Devices • Pack many gates into one chip! • Many connections available – Use the ones that the circuit needs! • PLD - generic terms – PLA - programmable logic arrays – PAL - programmable array logic (trademark) – FPGA - field-programmable gate arrays, newer technology • PLA specifications – Number of inputs, n – Number of outputs, m – Number of product terms, p Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Programmable Logic Devices • Pack many gates into one chip! • Many connections available – Use the ones that the circuit needs! • PLD - generic terms – PLA - programmable logic arrays – PAL - programmable array logic (trademark) – FPGA - field-programmable gate arrays, newer technology • PLA specifications – Number of inputs, n – Number of outputs, m – Number of product terms, p Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
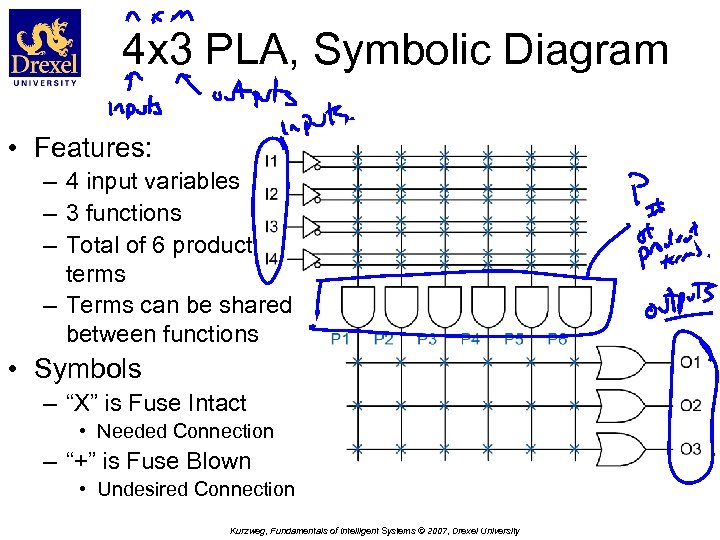 4 x 3 PLA, Symbolic Diagram • Features: – 4 input variables – 3 functions – Total of 6 product terms – Terms can be shared between functions • Symbols – “X” is Fuse Intact • Needed Connection – “+” is Fuse Blown • Undesired Connection Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
4 x 3 PLA, Symbolic Diagram • Features: – 4 input variables – 3 functions – Total of 6 product terms – Terms can be shared between functions • Symbols – “X” is Fuse Intact • Needed Connection – “+” is Fuse Blown • Undesired Connection Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
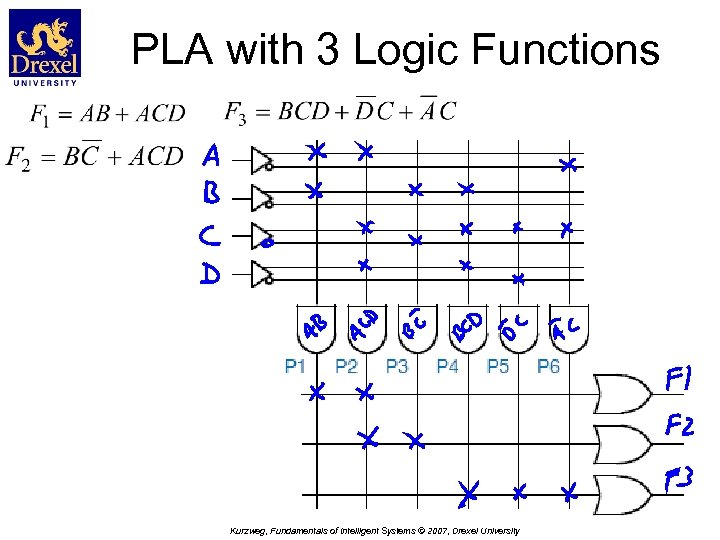 PLA with 3 Logic Functions Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
PLA with 3 Logic Functions Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
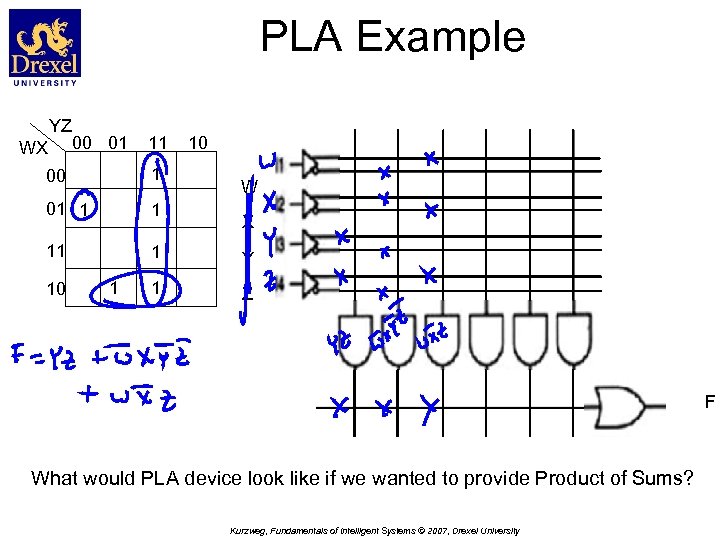 PLA Example YZ WX 00 01 11 10 00 1 01 1 1 11 1 Y 1 Z 10 1 W X F What would PLA device look like if we wanted to provide Product of Sums? Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
PLA Example YZ WX 00 01 11 10 00 1 01 1 1 11 1 Y 1 Z 10 1 W X F What would PLA device look like if we wanted to provide Product of Sums? Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
 Evolution of PLD’s • Current PLD’s are made with CMOS • Contain gates, FF’s, ROMS, adders, multiplies • Can be programmed and tested with on-chip circuits • Contain ~100, 000 gates • Whole system can be built on one chip • Problems with PLD? Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University
Evolution of PLD’s • Current PLD’s are made with CMOS • Contain gates, FF’s, ROMS, adders, multiplies • Can be programmed and tested with on-chip circuits • Contain ~100, 000 gates • Whole system can be built on one chip • Problems with PLD? Kurzweg, Fundamentals of Intelligent Systems © 2007, Drexel University


