ECDSA Elliptic Curve Digital Signature Algorithm Подготовили студенты

ECDSA (Elliptic Curve Digital Signature Algorithm) Подготовили студенты 698 группы: -Туктарова И. -Михеева А. -Бикмуллина Д. -Романова К.

ECDSA(определение) l l ECDSA (Elliptic Curve Digital Signature Algorithm) — алгоритм с открытым ключом для создания цифровой подписи, аналогичный по своему строению DSA, но определённый в отличие от него не над полем целых чисел, а в группе точек эллиптической кривой. Механизм электронной цифровой подписи (ЭЦП) возник как побочный эффект криптографии с открытым ключом. Поэтому характерное для систем с открытым ключом разделение ключа на 2 части - секретную и несекретную - позволяет реализовать возможность проверки подлинности без возможности подписать другой документ. Итак, цифровая подпись - это конечная цифровая последовательность, зависящая от самого сообщения или документа и от секретного ключа, известного только подписывающему субъекту, предназначенная для установления авторства. Так как цифровая подпись строится на базе криптосистемы с открытым ключом, то необходимо иметь пару ключей - секретный и открытый. Секретный ключ используется для формирования цифровой подписи, поэтому его нужно хранить в тайне. А открытый ключ используется для проверки соответствия подписи документу, поэтому он должен быть опубликован, например, в общедоступном каталоге.

Особенности l l Стойкость алгоритма шифрования основывается на проблеме дискретного логарифма в группе точек эллиптической кривой. В отличие от проблемы простого дискретного логарифма и проблемы факторизации целого числа, не существует субэкспонециального алгоритма для проблемы дискретного логарифма в группе точек эллиптической кривой. По этой причине «сила на один бит ключа» существенно выше в алгоритме, который использует эллиптические кривые. Д. Брауном (Daniel R. L. Brown) было доказано, что алгоритм ECDSA не является более безопасным, чем DSA. Им было сформулировано ограничение безопасности для ECDSA, которое привело к следующему заключению: «Если группа эллиптической кривой может быть смоделирована основной группой и ее хэш-функция удовлетворяет определенному обоснованному предположению, то ECDSA устойчива к chosen-message атаке с существующей фальсификацией. » Алгоритм ECDSA в 1999 г. был принят, как стандарт ANSI, в 2000 г. — как стандарт IEEE и NIST. Также в 1998 г. алгоритм был принят стандартом ISO. Несмотря на то, что стандарты ЭЦП созданы совсем недавно и находятся на этапе совершенствования, одним наиболее перспективных из них на сегодняшний день является ANSI X 9. 62 ECDSA от 1999 — DSA для эллиптических кривых.

Выбор параметров l Для подписывания сообщений необходима пара ключей — открытый и закрытый. При этом закрытый ключ должен быть известен только тому, кто подписывает сообщения, а открытый — любому желающему проверить подлинность сообщения. Также общедоступными являются параметры самого алгоритма.

Параметры алгоритма 1. Выбор хэш-функции H(x). Для использования алгоритма необходимо, чтобы подписываемое сообщение являлось числом. Хеш-функция должна преобразовать любое сообщение в последователность битов, которые можно потом преобразовать в число. 2. Выбор большого простого числа q — порядок одной из циклических подгруппы точек эллиптической кривой. Замечание: Если размерность этого числа в битах меньше размерности в битах значений хэш-функции H(x) то используются только левые биты значения хэш-функции. 3. Простым числом p обозначается характеристика поля координат Fp.

Генерирование ключей ECDSA(1) l l l Для простоты будем рассматривать эллиптические кривые над полем Fp, где Fp — конечное простое поле. Причем, если необходимо, конструкцию можно легко адаптировать для эллиптических кривых над другим полем. Пусть E — эллиптическая кривая, определенная над Fp, и P — точка простого порядка q кривой E(Fp). Кривая E и точка P являются системными параметрами. Число p — простое. Каждая пользовательница Алиса конструирует свой ключ посредством следующих действий: Выбирает случайное или псевдослучайное целое число x из интервала [1, q − 1]. Вычисляет произведение (кратное) Q = x·P. Открытым ключом пользовательницы Алисы A является точка Q, а закрытым — x.

Генерирование ключей ECDSA(2) l l l Вместо использования E и P в качестве глобальных системных параметров, можно фиксировать только поле Fp для всех пользователей и позволить каждому пользователю выбирать свою собственную эллиптическую кривую E и точку P E(Fp). В этом случае определенное уравнение кривой E, координаты точки P, а также порядок q этой точки P должны быть включены в открытый ключ пользователя. Если поле Fp фиксировано, то аппаратная и программная составляющие могут быть построены так, чтобы оптимизировать вычисления в том поле. В то же время имеется огромное количество вариантов выбора эллиптической кривой над полем Fp. Пусть дан простой модуль m. Требуется для каждого числа в отрезке [1; m-1] найти обратное к нему. Применяя описанные выше алгоритмы, мы получим лишь решения с асимптотикой O(m logm). Здесь же мы приведём простое решение с асимптотикой O(m).

Решение это выглядит следующим образом. Обозначим через r[i] искомое i обратное к числу m по модулю. Тогда для i>1 верно тождество: Реализация этого удивительно лаконичного решения: l l l r[1] = 1; for (int i=2; i

Вычисление цифровой подписи l l l l Для того, чтобы подписать какое-либо сообщение, для которого подсчитано значение h хэш-функции H, пользователь A должен сделать следующее: Выбрать случайное целое число kЄ [1; q-1] Вычислить и положить в , где r получается из целого числа x 1 между 0 и (p − 1) приведением по модулю q. Замечание: если r = 0, то уравнение подписи не зависит от секретного ключа x, и следовательно, (r, s) не подходит в качестве цифровой подписи. Значит, в случае r = 0 необходимо вернуться к шагу 1. Вычислить k (− 1)(mod q) и положить , где h — значение хеш-функции подписываемого сообщения. Замечание: если s = 0, то значение s (− 1)(mod q), нужное для проверки, не существует. Значит, в случае s = 0 необходимо вернуться к шагу 1. Подписью для сообщения является пара целых чисел (r, s).

Проверка цифровой подписи(1) l l l Для того, чтобы проверить подпись пользовательницы Алисы (r, s) на сообщение, пользователь Борис B должен сделать следующее: Получить подтвержденную копию открытого ключа Q пользовательницы А; Проверить, что числа r и s являются целыми числами из интервала [1, q − 1], и вычислить значение хеш-функции h от сообщения; Вычислить и ; Вычислить , и относительно x 0, как целого числа между 0 и (p − 1), положить ; Принять подпись, если и только если v = r.

Проверка цифровой подписи(2) l Заметим, что, если пользовательница Алиса вычислила свою подпись правильно, то , так как k = s − 1(h + xr)(mod q), и поэтому v = r. l Для подтверждения публичного ключа Q нужно проделать следующее (O здесь обозначает бесконечно удалённую точку): l Проверить, что Q не равно O и координаты верны; l Проверить, что Q лежит на кривой; l Проверить, что q. Q = O;

Генерация главных параметров l l l l Один из способом генерирования криптографически надежных параметров заключается в следующем: Выбираем коэффициенты a и b специфическим образом используя в вычислениях случайные/псевдослучайные числа. Пусть E — эллиптическая кривая — y 2 = x 3 + ax + b; Вычисляем ; Проверяем, что N имеет делитель, который является большим простым числом q(q > 2160 и. Если нет, то нужно вернуться на шаг 1. Проверяем, что q не делит pk − 1 для каждого k, . Если нет, то нужно вернуться на шаг 1; Проверяем, что . Если нет, то нужно вернуть на шаг 1; Берем случайную точку и положить G = (N / q)G'. Повторяем до тех пор пока.

Преимущества ECDSA над DSA l ECDSA является очень привлекательным алгоритмом для реализации ЭЦП. Самым важным преимуществом ECDSA является возможность его работы на значительно меньших полях Fp. Как, в общем, с криптографией эллиптической кривой, предполагается, что битовый размер открытого ключа, который будет необходим для ECDSA, равен двойному размеру секретного ключа в битах. Для сравнения, при уровне безопасности в 80 бит (то есть атакующему необходимо примерно 280 версий подписи для нахождения секретного ключа), размер открытого ключа DSA равен, по крайней мере, 1024 бит, когда как открытого ключа ECDSA — 160 бит. С другой стороны размер подписи одинаков и для DSA, и для ECDSA: 4 t бит, где t — уровень безопасности, измеренный в битах, то есть — примерно 320 бит для уровня безопасности в 80 бит.

Cлабость цифровой подписи ECDSA(1) l Есть мнение, что новый стандарт небезопасен, так как позволяет имитировать подмену подписи. По его мнению, недостаток ECDSA в том, что этот стандарт позволяет рядовому пользователю выбрать свои секретный и открытый ключи так, что подписи для двух известных заранее сообщений совпадут. А это открывает простор для различных махинаций с использованием ЭЦП. Возможность имитации подделки основывается на том, что x-координаты противоположных точек эллиптических кривых совпадают. Если q. G=0, то (q-1)G = -G, следовательно справедливы равенства: c 1 = x. G = c 2 = x(q-1)G = c, где 0 - бесконечно удаленная точка эллиптической кривой (нейтральный элемент относительно операции +). Положим случайные вычеты q 1 и q 2 равными 1 и (q-1). Отметим также, что (q-1)-1 = (q-1) (mod q). Подберем две одинаковые подписи для сообщений m 1 и m 2. Уравнения подписи имеют вид:

Cлабость цифровой подписи ECDSA(2) l d 1 = u 1 -1 (m 1 + sc) (mod q) = (m 1 + sc) (mod q) d 2 = u 2 -1 (m 2 + sc) (mod q) = (q-1)(m 2 + sc) (mod q) Нам нужно, чтобы выполнялось равенство d 1 = d 2. Получим уравнение: m 1+sc = (q-1)(m 2 +sc) (mod q) Отсюда легко находится s: 2 cs = (q-1)(m 1 + m 2) (mod q) l Так как q - простое число, то это уравнение однозначно разрешимо относительно s. Таким образом, мы получили две одинаковые подписи для двух заранее выбранных сообщений. Практическая реализация - на сегодняшний день реализация электронных цифровых подписей осуществляются программным образом. Для создания подобных продуктов используют специальные программные пакеты, позволяющие создавать криптографические приложения с использованием различных внешних устройств безопасности

Основные проблемы криптостойкости: l l l Проблема нахождения закрытого ключа является проблемой нахождения дискретного логарифма в группе точек эллиптической кривой определенной над простым полем. Стойкость протоколов криптографии на эллиптических кривых в конечных полях основана на сложности решения проблемы дискретного логарифма. Эта проблема имеет место в каждом случае, когда задана некоторая циклическая группа G с образующим элементом a. Тогда любой элемент y G может быть вычислен как: y = ax, где x Z (Z – кольцо целых чисел). При известном x вычислить y довольно легко, а сделать обратное преобразование, то есть вычислить x по известному y очень трудно. Под словами очень трудно здесь понимается отсутствие алгоритма решения данной задачи за субполиномиальное время (практически задача может быть решена полным перебором). Криптосистемы цифровой подписи на основе эллиптических кривых с длиной ключа 160 бит имеют одинаковую стойкость с криптосистемами DSA и Эль-Гамаля с длиной ключа 1024 бита. Очевидно, что в ближайшем будущем данные системы займут доминирующее положение в криптографии с открытым ключом. Однако, при их широком распространении и применении, большие силы криптоаналитиков будут направлены на поиск новых, более быстрых, алгоритмов решения проблемы дискретного логарифма в группе точек эллиптических кривых. Скорее всего такие алгоритмы будут найдены, как это уже произошло с проблемами разложения больших чисел на множители (RSA) или дискретного логарифма в простом поле (DSA, Эль-Гамаль).

Схемы электронной цифровой подписи Аппарат электронной цифровой подписи позволяет решать задачи проверки целостности и их авторства (без возможности отречения), разумеется, если используются стойкие алгоритмы формирования ЭЦП, надежные криптографические протоколы и сохранен в тайне секретный ключ. Поэтому для того, чтобы документы, подписанные ЭЦП, имели юридическую силу, развитые государства принимают стандарты на алгоритмы ЭЦП, кроме того, существует ряд коммерческих алгоритмов, которые хоть в среднем и слабее национальных, однако достаточно надежны для коммерческого уровня при разумном выборе длины ключей. Ниже будут описаны 9 алгоритмов формирования цифровой подписи:

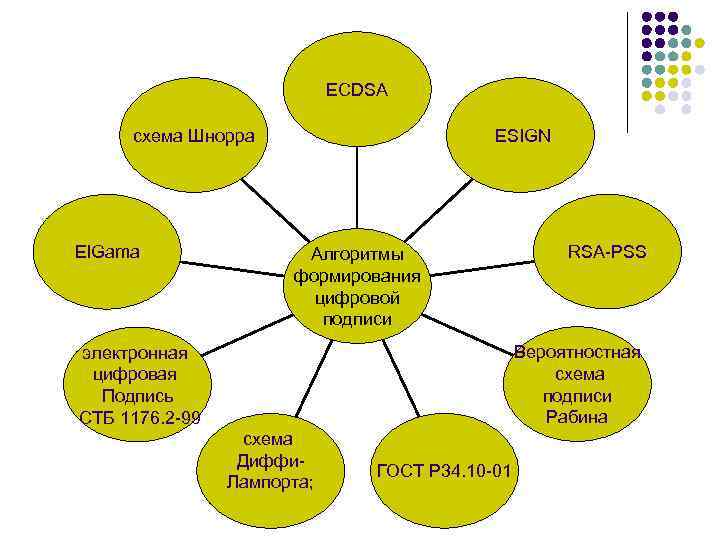ECDSA схема Шнорра El. Gama ESIGN Алгоритмы формирования цифровой подписи RSA-PSS Вероятностная схема подписи Рабина электронная цифровая Подпись СТБ 1176. 2 -99 схема Диффи. Лампорта; ГОСТ Р 34. 10 -01

Список литературы: l l 1. Коржев В. Цифровая подпись. Эллиптические кривые. «Открытые системы» (8 августа 2002). 2. D. Brown Generic groups, collision resistance, and ECDSA. «Codes and Cryptography» (26 февраля 2002).

СПАСИБО ЗА ВНИМАНИЕ.