b576386b9002428049901e84e450867d.ppt
- Количество слайдов: 86

Earthquake Engineering Research at UC Berkeley and Recent Developments at CSI Berkeley BY Ed Wilson Professor Emeritus of Civil Engineering University of California, Berkeley October 24 - 25, 2008

Summary of Presentation 1. UC Berkeley in the period of 1953 to 1991 2. The Faculty 3. The SAP Series of Computer Programs 4. Dynamic Field Testing of Structures 5. The Load-Dependent Ritz Vectors – LDR Vectors - 1980 6. The Fast Nonlinear Analysis Method – FNA Method - 1990 7. A New Efficient Algorithm for the Evaluation of All Static and Dynamic Eigenvalues of any Structure - 2002 9. Final Remarks and Recommendations All Slides can be copied from we site edwilson. org

“edwilson. org” Copy Papers and Slides Early Finite Element Research at UC Berkeley by Ray Clough and Ed Wilson The Development of Earthquake Engineering Software at Berkeley by Ed Wilson - Slides

Dynamic Research at UC Berkeley Retired Faculty Members by Date Hired 1946 Bob Wiegel – Coastal Engineering - Tsunamis 1949 Ray Clough – Computational and Experimental Dynamics 1950 Harry Seed – Soil Mechanics - Liquefaction 1953 Joseph Penzien – Random Vibrations – Wind, Waves & Earthquake 1957 Jack Bouwkamp – Dynamic Field Testing of Real Structures 1963 Robert Taylor – Computational Solid and Fluid Dynamics 1965 James Kelly – Base Isolation and Energy Dissipation 1965 Ed Wilson – Numerical Algorithms for Dynamic Analysis 196? Beresford Parlett – Mathematics - Numerical Methods 196? Bruce Bolt – Seismology – Earthquake Ground Motions

Professor Ray W. Clough 1942 BS University of Washington 1943 - 1946 U. S. Army Air Force 1946 - 1949 MIT - D. Science - Bisplinghoff 1949 - 1986 Professor of CE U. C Berkeley 1952 and 1953 Summer Work at Boeing National Academy of Engineering National Academy of Science Presidential Medal of Science The Franklin Institute Medal – April 27, 2006

Doug, Shirley and Ray Clough The Franklin Institute Awards – April 27, 2006

Joe Penzien 1945 BS University of Washington 1945 US Army Corps of Engineers 1946 Instructor - University of Washington 1953 MIT - D. Science 1953 - 88 Professor UCB 1990 - 2006 International Civil Engineering Consultants – Principal with Dr. Wen Tseng

Professor Joe Penzien – First Director of EERC at UC Berkeley The Franklin Institute Awards – April 27, 2006

New Printing of the Clough and Penzien Book Berkeley, CA, February 26, 2004 – Computers and Structures, Inc. , is pleased to release the latest revision to Dynamics of Structures, 2 nd Edition by Professors Clough and Penzien. A classic, this definitive textbook has been popular with educators worldwide for nearly 30 years. This release has been updated by the original authors to reflect the latest approaches and techniques in the field of structural dynamics for civil engineers. csiberkeley. com Ask for Educational Discount

Ed Wilson - edwilson. org 1955 BS University of California 1955 - 57 US Army – 15 months in Korea 1958 MS UCB 1957 - 59 Oroville Dam Experimental Project 1960 First Automated Finite Element Program 1963 D Eng UCB 1963 - 1965 Research Engineer, Aerojet - 10 g Loading 1965 - 1991 Professor UCB – 29 Ph. D Students 1991 - 2008 Senior Consultant To CSI Berkeley – where 95% of my work is in Earthquake Engineering

My Book – 23 Chapters csiberkeley. com Ask for Educational Discount

NINETEEN SIXTIES IN BERKELEY 1. Cold War - Blast Analysis 2. Earthquake Engineering Research 3. State And Federal Freeway System 4. Manned Space Program 5. Offshore Drilling 6. Nuclear Reactors And Cooling Towers

NINETEEN SIXTIES IN BERKELEY 1. Period Of Very High Productivity 2. No Formal Research Institute 3. Free Exchange Of Information – Gave programs to profession prior to publication 4. Worked Closely With Mathematics Group 5. Students Were Very Successful

UC Students “Berkeley During The Late 1960’s And Early 1970’s Graduate Study Was Like Visiting An Intellectual Candy Store” Thomas Hughes Professor, University of Texas

SAP STRUCTURAL ANALYSIS PROGRAM ALSO A PERSON “ Who Is Easily Deceived Or Fooled” “ Who Unquestioningly Serves Another”

From The Foreword Of The First SAP Manual "The slang name S A P was selected to remind the user that this program, like all programs, lacks intelligence. It is the responsibility of the engineer to idealize the structure correctly and assume responsibility for the results. ” Ed Wilson 1970

The SAP Series of Programs 1969 - 70 SAP Used Static Loads to Generate Ritz Vectors 1971 - 72 Solid-Sap Rewritten by Ed Wilson 1972 -73 SAP IV 1973 – 74 Subspace Iteration – Dr. Jűgen Bathe NON SAP New Program – The Start of ADINA Lost All Research and Development Funding 1979 – 80 SAP 80 New Linear Program for Personal Computers 1983 – 1987 SAP 80 CSI added Pre and Post Processing 1987 - 1990 SAP 90 Significant Modification and Documentation 1997 – Present SAP 2000 Nonlinear Elements – More Options – With Windows Interface

FIELD MEASUREMENTS REQUIRED TO VERIFY 1. MODELING ASSUMPTIONS 2. SOIL-STRUCTURE MODEL 3. COMPUTER PROGRAM 4. COMPUTER USER

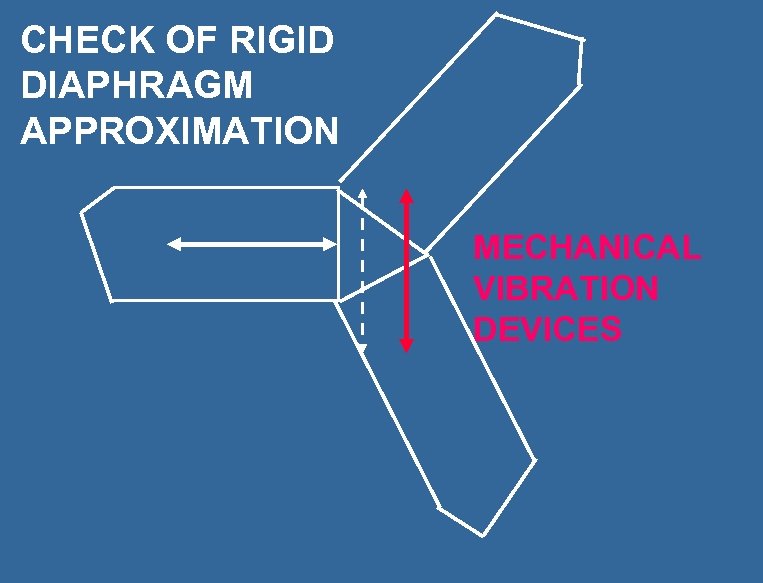
CHECK OF RIGID DIAPHRAGM APPROXIMATION MECHANICAL VIBRATION DEVICES
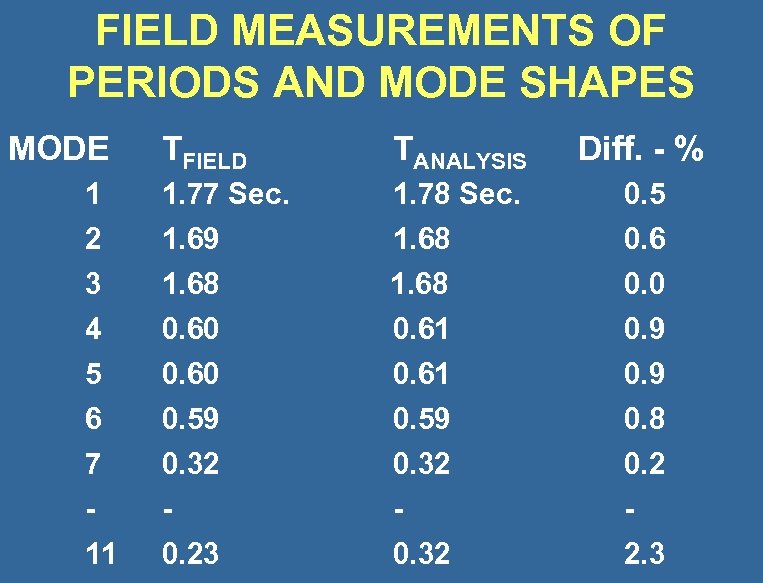
FIELD MEASUREMENTS OF PERIODS AND MODE SHAPES MODE TFIELD TANALYSIS Diff. - % 1 2 3 4 5 6 7 1. 77 Sec. 1. 69 1. 68 0. 60 0. 59 0. 32 1. 78 Sec. 1. 68 0. 61 0. 59 0. 32 0. 5 0. 6 0. 0 0. 9 0. 8 0. 2 11 0. 23 0. 32 2. 3
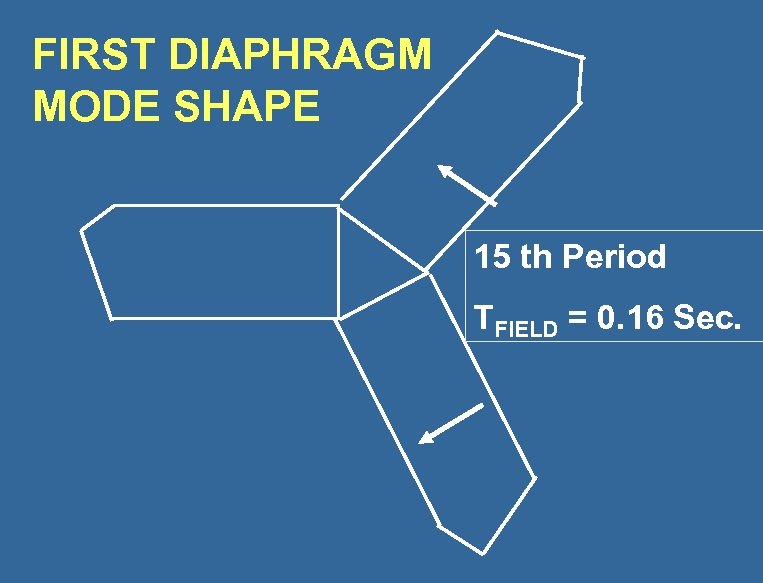
FIRST DIAPHRAGM MODE SHAPE 15 th Period TFIELD = 0. 16 Sec.

Load-Dependent Ritz Vectors LDR Vectors - 1980

DYNAMIC EQUILIBRIUM EQUATIONS M a + C v + K u = F(t) a v u M C K F(t) = = = = Node Accelerations Node Velocities Node Displacements Node Mass Matrix Damping Matrix Stiffness Matrix Time-Dependent Forces

PROBLEM TO BE SOLVED Ma + Cv+ Ku = fi g(t)i = - Mx a x - M y a y - Mz a z For 3 D Earthquake Loading THE OBJECTIVE OF THE ANALYSIS IS TO SOLVE FOR ACCURATE DISPLACEMENTS and MEMBER FORCES

METHODS OF DYNAMIC ANALYSIS For Both Linear and Nonlinear Systems ÷ STEP BY STEP INTEGRATION - 0, dt, 2 dt. . . N dt USE OF MODE SUPERPOSITION WITH EIGEN OR LOAD-DEPENDENT RITZ VECTORS FOR FNA For Linear Systems Only TRANSFORMATION TO THE FREQUENCY ÷ DOMAIN and FFT METHODS RESPONSE SPECTRUM METHOD - CQC - SRSS

STEP BY STEP SOLUTION METHOD 1. Form Effective Stiffness Matrix 2. Solve Set Of Dynamic Equilibrium Equations For Displacements At Each Time Step 3. For Non Linear Problems Calculate Member Forces For Each Time Step and Iterate for Equilibrium - Brute Force Method

MODE SUPERPOSITION METHOD 1. Generate Orthogonal Dependent Vectors And Frequencies 2. Form Uncoupled Modal Equations And Solve Using An Exact Method For Each Time Increment. 3. Recover Node Displacements As a Function of Time 4. Calculate Member Forces As a Function of Time

GENERATION DEPENDENT LOAD VECTORS OF RITZ 1. Approximately Three Times Faster Than The Calculation Of Exact Eigenvectors 2. Results In Improved Accuracy Using A Smaller Number Of LDR Vectors 3. Computer Storage Requirements Reduced 4. Can Be Used For Nonlinear Analysis To Capture Local Static Response

STEP 1. INITIAL CALCULATION A. TRIANGULARIZE STIFFNESS MATRIX B. DUE TO A BLOCK OF STATIC LOAD VECTORS, f, SOLVE FOR A BLOCK OF DISPLACEMENTS, u, Ku=f C. MAKE FORM u STIFFNESS AND MASS ORTHOGONAL TO FIRST BLOCK OF LDL VECTORS V 1 T M V 1 = I

STEP 2. VECTOR GENERATION i = 2. . N Blocks A. Solve for Block of Vectors, K Xi = M Vi-1 B. Make Vector Block, Xi , Stiffness and Mass Orthogonal - Yi C. Use Modified Gram-Schmidt, Twice, to Make Block of Vectors, Yi , Orthogonal to all Previously Calculated Vectors - Vi

STEP 3. MAKE VECTORS STIFFNESS ORTHOGONAL A. SOLVE Nb x Nb Eigenvalue Problem [ V T K V ] Z = [ w 2 ] Z B. CALCULATE MASS AND STIFFNESS ORTHOGONAL LDR VECTORS VR = V Z =
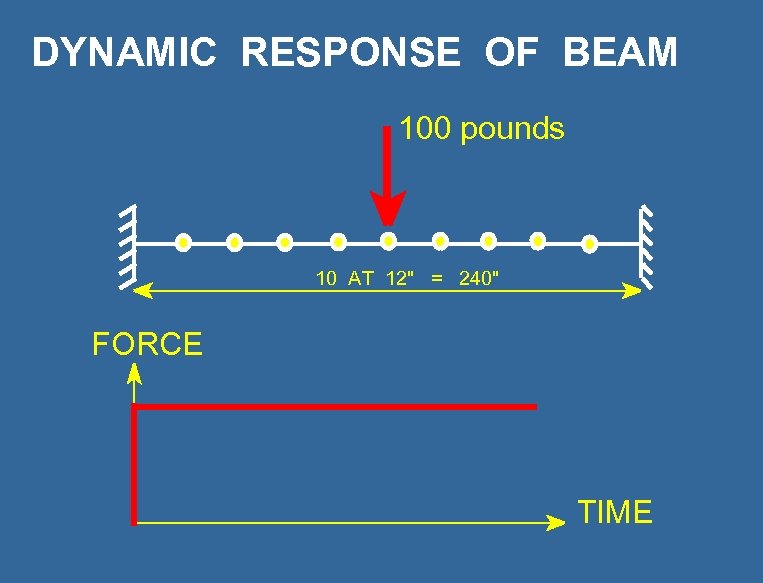
DYNAMIC RESPONSE OF BEAM 100 pounds 10 AT 12" = 240" FORCE TIME
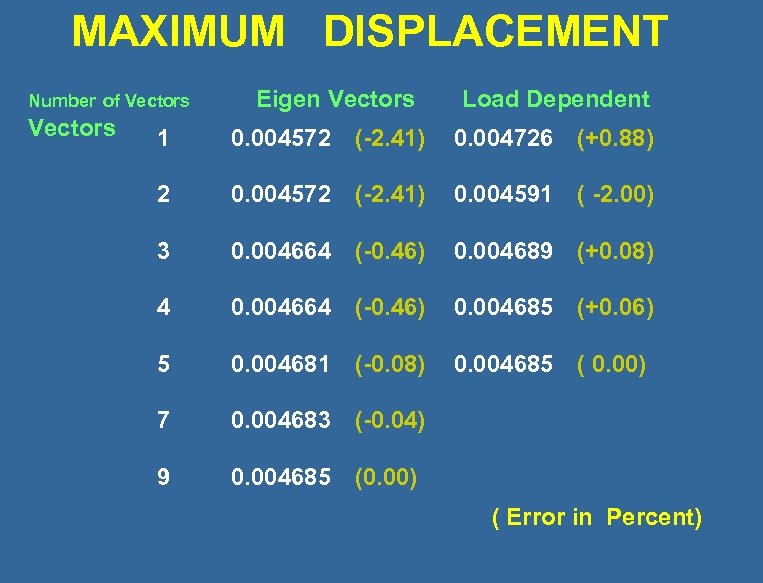
MAXIMUM DISPLACEMENT Number of Vectors Eigen Vectors Load Dependent 1 0. 004572 (-2. 41) 0. 004726 (+0. 88) 2 0. 004572 (-2. 41) 0. 004591 ( -2. 00) 3 0. 004664 (-0. 46) 0. 004689 (+0. 08) 4 0. 004664 (-0. 46) 0. 004685 (+0. 06) 5 0. 004681 (-0. 08) 0. 004685 ( 0. 00) 7 0. 004683 (-0. 04) 9 0. 004685 (0. 00) ( Error in Percent)

MAXIMUM MOMENT Number of Vectors 1 Eigen Vectors Load Dependent 4178 ( - 22. 8 %) 5907 ( + 9. 2 ) 2 4178 ( - 22. 8 ) 5563 ( + 2. 8 ) 3 4946 ( - 8. 5 ) 5603 ( + 3. 5 ) 4 4946 ( - 8. 5 ) 5507 ( + 1. 8) 5 5188 ( - 4. 1 ) 5411 ( 0. 0 ) 7 5304 ( -. 0 ) 9 5411 ( 0. 0 ) ( Error in Percent )

LDR Vector Summary After Over 20 Years Experience Using the LDR Vector Algorithm We Have Always Obtained More Accurate Displacements and Stresses Compared to Using the Same Number of Exact Dynamic Eigenvectors. SAP 2000 has Both Options

The Fast Nonlinear Analysis Method The FNA Method was Named in 1996 Designed for the Dynamic Analysis of Structures with a Limited Number of Predefined Nonlinear Elements

FAST NONLINEAR ANALYSIS 1. EVALUATE LDR VECTORS WITH NONLINEAR ELEMENTS REMOVED AND DUMMY ELEMENTS ADDED FOR STABILITY 2. SOLVE ALL MODAL EQUATIONS WITH NONLINEAR FORCES ON THE RIGHT HAND SIDE 3. USE EXACT INTEGRATION WITHIN EACH TIME STEP 4. FORCE AND ENERGY EQUILIBRIUM ARE STATISFIED AT EACH TIME STEP BY ITERATION
BASE ISOLATION Isolators
BUILDING IMPACT ANALYSIS
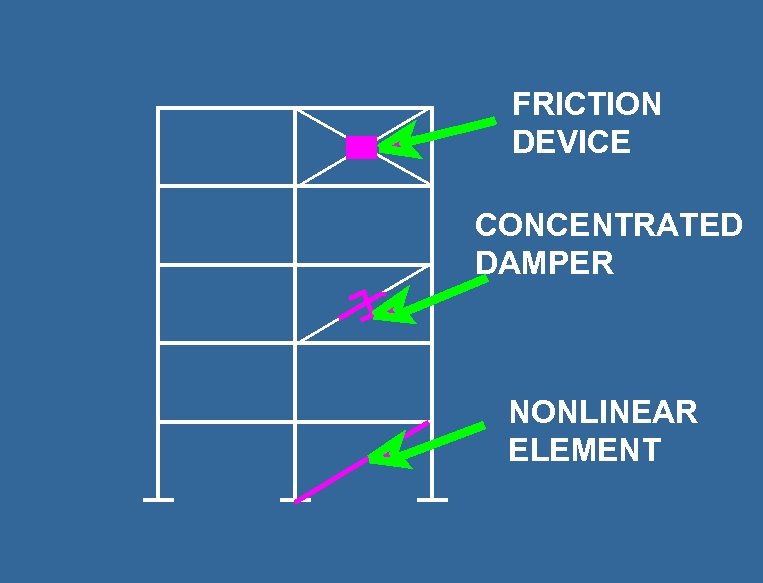
FRICTION DEVICE CONCENTRATED DAMPER NONLINEAR ELEMENT
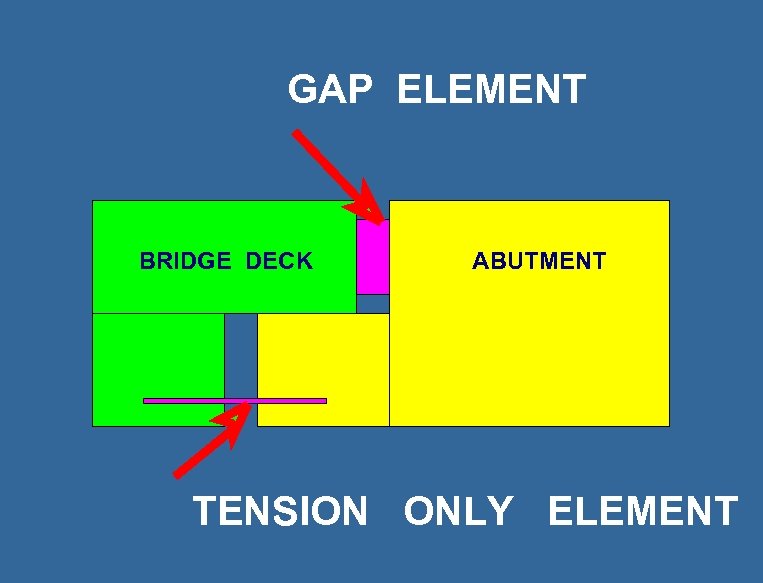
GAP ELEMENT BRIDGE DECK ABUTMENT TENSION ONLY ELEMENT
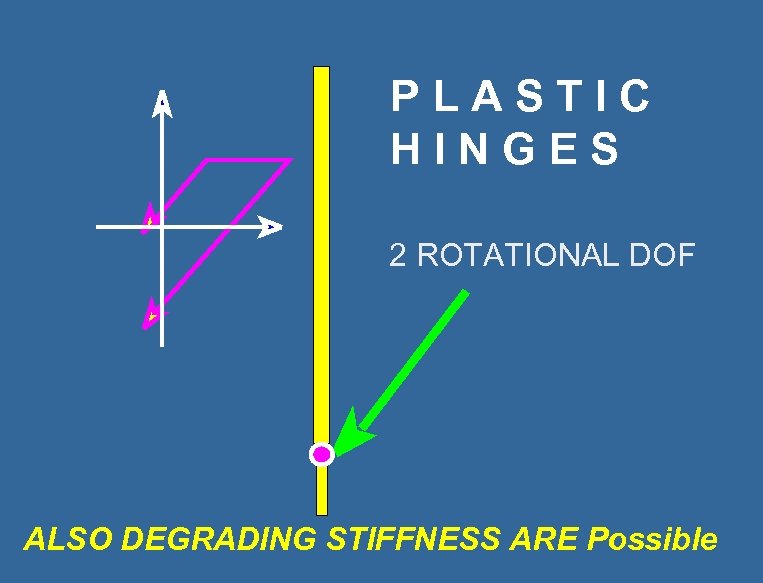
PLASTIC HINGES 2 ROTATIONAL DOF ALSO DEGRADING STIFFNESS ARE Possible
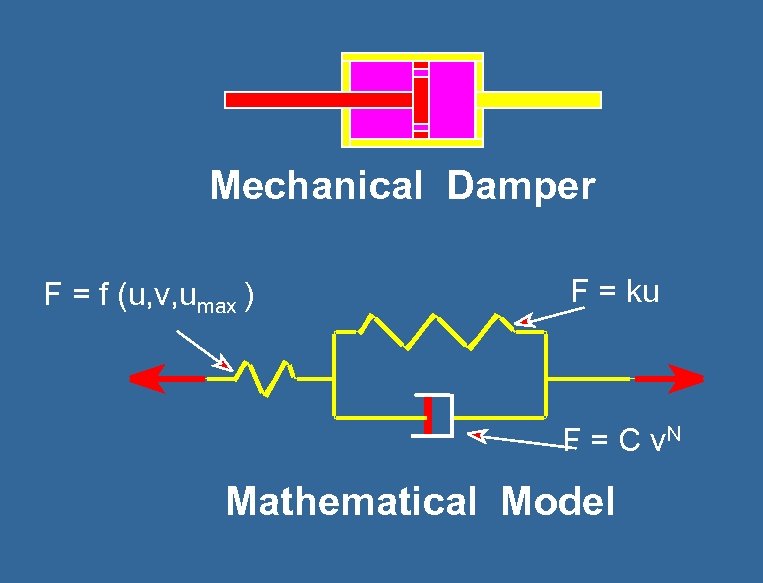
Mechanical Damper F = f (u, v, umax ) F = ku F = C v. N Mathematical Model

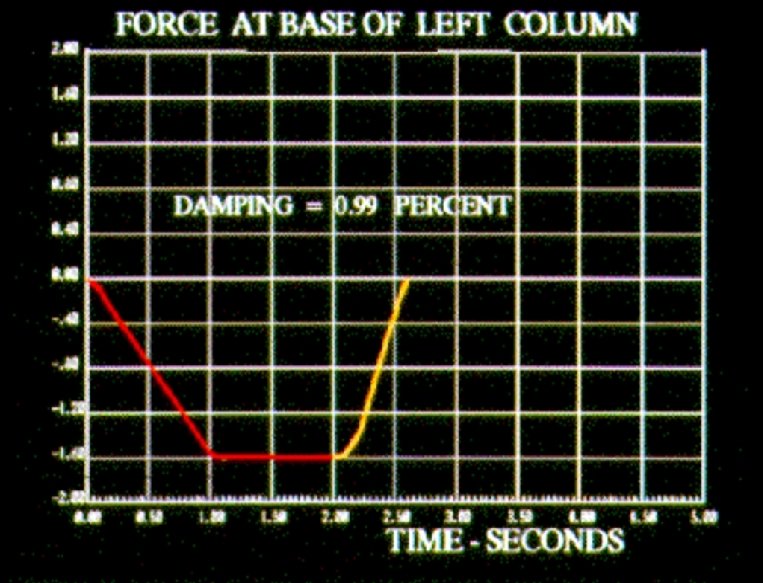
LINEAR VISCOUS DAMPING DOES NOT EXIST IN NORMAL STRUCTURES AND FOUNDATIONS 5 OR 10 PERCENT MODAL DAMPING VALUES ARE OFTEN USED TO JUSTIFY ENERGY DISSIPATION DUE TO NONLINEAR EFFECTS IF ENERGY DISSIPATION DEVICES ARE USED THEN 1 PERCENT MODAL DAMPING SHOULD BE USED FOR THE ELASTIC PART OF THE STRUCTURE - CHECK ENERGY PLOTS
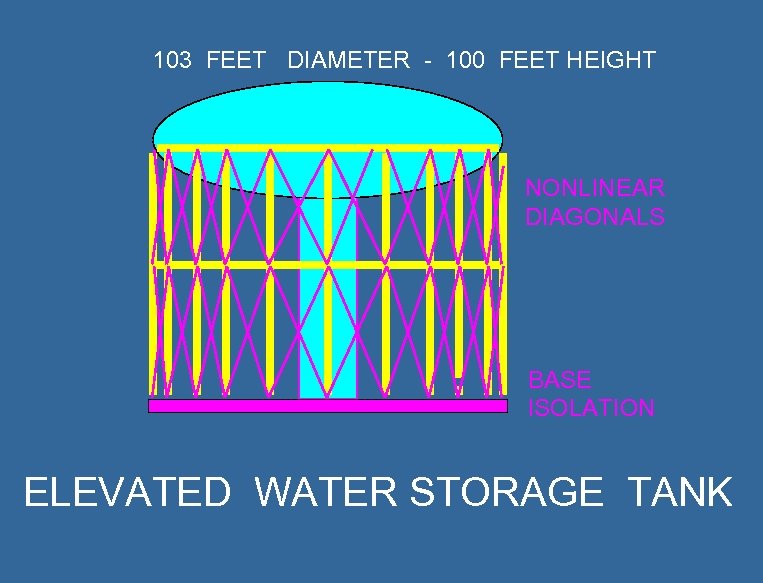
103 FEET DIAMETER - 100 FEET HEIGHT NONLINEAR DIAGONALS BASE ISOLATION ELEVATED WATER STORAGE TANK

COMPUTER MODEL 92 NODES 103 ELASTIC FRAME ELEMENTS 56 NONLINEAR DIAGONAL ELEMENTS 600 TIME STEPS @ 0. 02 Seconds

COMPUTER TIME REQUIREMENTS PROGRAM ANSYS INTEL 486 3 Days ANSYS CRAY 3 Hours SADSAP INTEL 486 ( B Array was 56 x 20 ) ( 4300 Minutes ) ( 180 Minutes ) 2 Minutes

Nonlinear Equilibrium Equations

Summary Of FNA Method Calculate Load-Dependant Ritz Vectors for Structure With Nonlinear Elements Removed. These Vectors Satisfy the Following Orthogonality Properties

The Solution Is Assumed to Be a Linear Combination of the LDR Vectors. Or, Which Is the Standard Mode Superposition Equation Remember the LDR Vectors Are a Linear Combination of the Exact Eigenvectors; Plus, the Static Displacement Vectors. No Additional Approximations Are Made.

A typical modal equation is uncoupled. However, the modes are coupled by the unknown nonlinear modal forces which are of the following form: The deformations in the nonlinear elements can be calculated from the following displacement transformation equation:

Since the deformations in the nonlinear elements can be expressed in terms of the modal response by Where the size of the array is equal to the number of deformations times the number of LDR vectors. The array is calculated only once prior to the start of mode integration. THE ARRAY CAN BE STORED IN RAM

The nonlinear element forces are calculated, for iteration i , at the end of each time step t
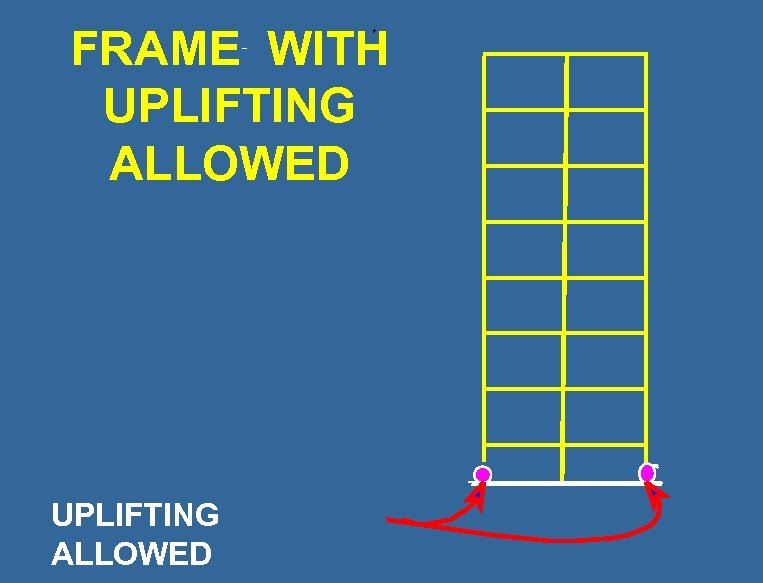
FRAME WITH UPLIFTING ALLOWED
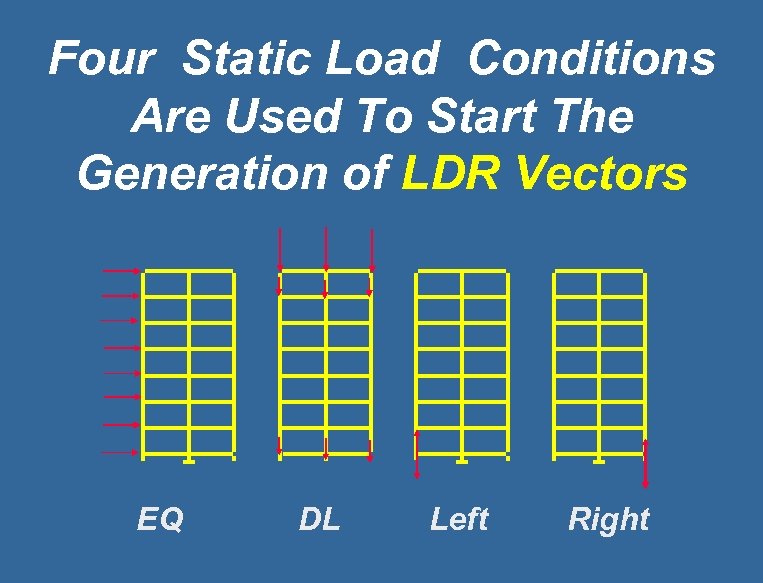
Four Static Load Conditions Are Used To Start The Generation of LDR Vectors EQ DL Left Right
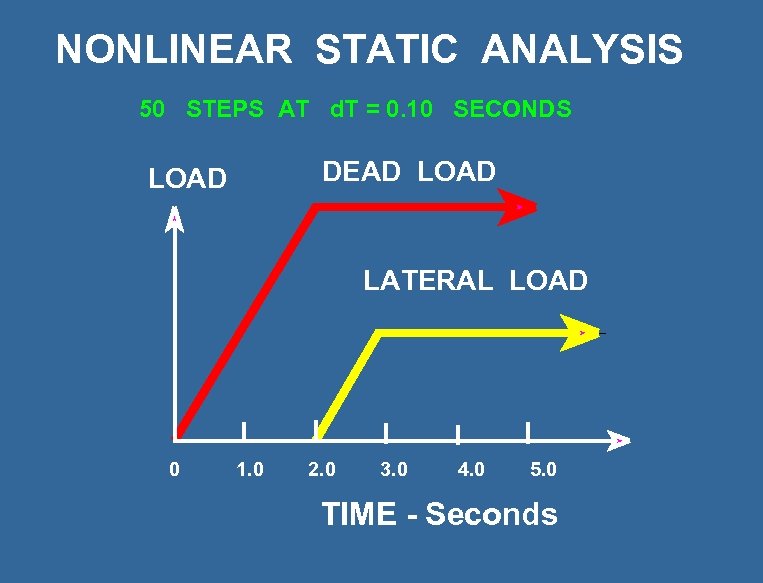
NONLINEAR STATIC ANALYSIS 50 STEPS AT d. T = 0. 10 SECONDS DEAD LOAD LATERAL LOAD 0 1. 0 2. 0 3. 0 4. 0 5. 0 TIME - Seconds
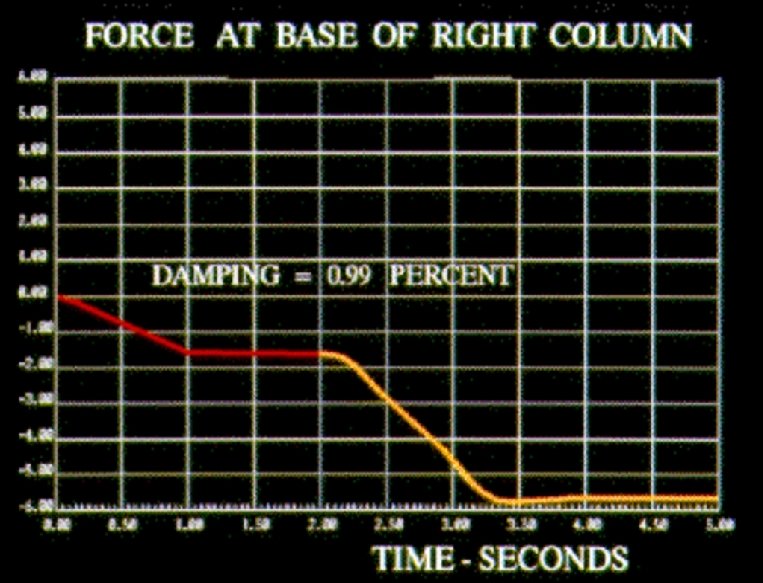
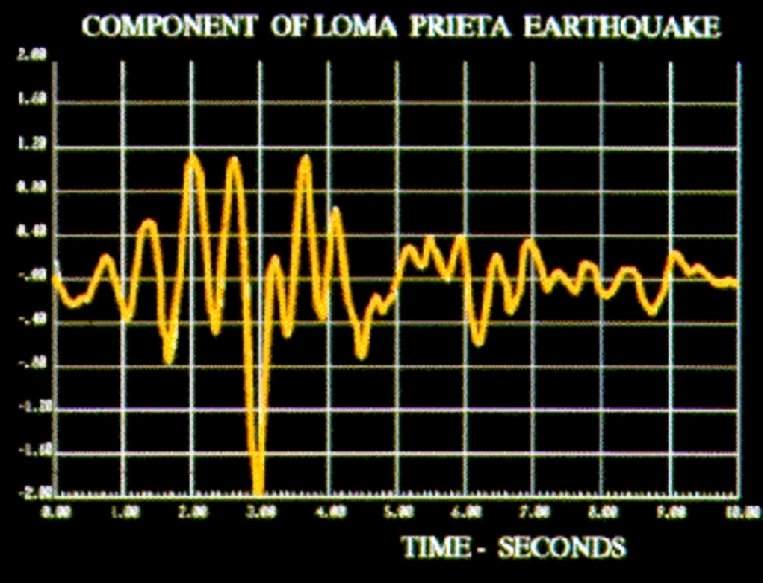
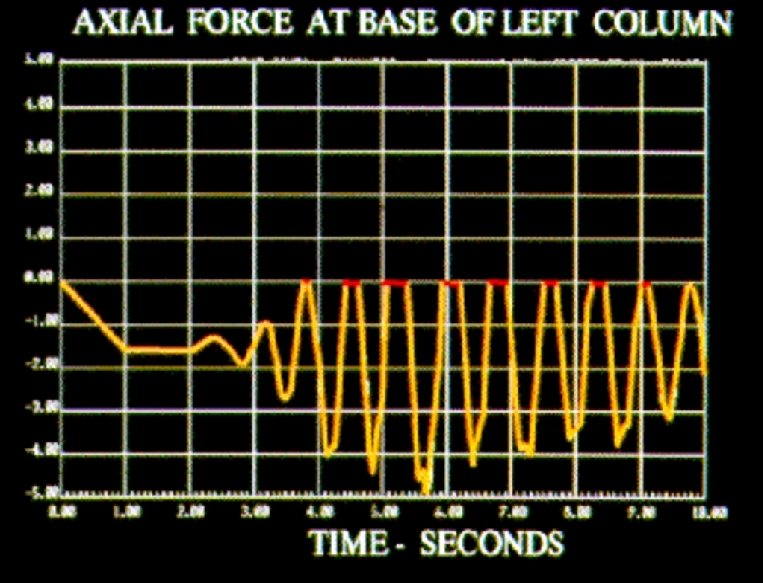

Advantages Of The FNA Method 1. The Method Can Be Used For Both Static And Dynamic Nonlinear Analyses 2. The Method Is Very Efficient And Requires A Small Amount Of Additional Computer Time As Compared To Linear Analysis 2. The Method Can Easily Be Incorporated Into Existing Computer Programs For LINEAR DYNAMIC ANALYSIS.

A COMPLETE EIGENVECTOR SUBSPACE FOR THE LINEAR AND NONLINEAR DYNAMIC ANALYSIS OF STRUCTURES

Definition Of Natural Eigenvectors The total number of Natural Eigenvectors that exist is always equal to the total number of displacement degrees-of-freedom of the structural system. The following three types of Natural Eigenvectors are possible: Rigid Body Vectors Dynamic Vectors Static Vectors
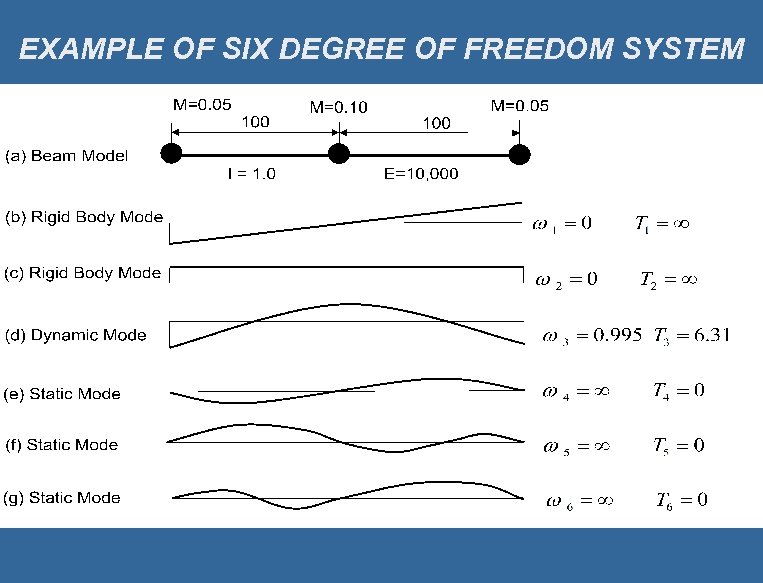
EXAMPLE OF SIX DEGREE OF FREEDOM SYSTEM

How Do We Solve a System That Has Both Zero and Infinite Frequencies?

Solve Static and Dynamic Equilibrium Equations by Mode Superposition The Modal Equations Can Now Be Written As

SOLUTION OF TYPICAL MODAL EQUATION FOR DYNAMIC MODES, USE PIECE-WISE EXACT SOLUTION FOR RIGID-BODY MODES, Direct INTEGRATION FOR STATIC MODES, THE SOLUTION IS

Calculation of Frequencies from Natural Eigenvalues

Eigenvalues for Simple Beam Mode Natural Eigenvalue 1 2 3 4 5 6 100 0. 826 0 0 0 Frequency 0 0 0. 995 Period 6. 31 0 0 0

CALCULATION OF NATURAL EIGENVECTORS Use Recurrence Equation Of Following Form The First Load Block Must Be The Static Load Patterns Acting on The Structure Subsequent Load Blocks Are Calculated From Iteration Is Not Required

The Natural Eigenvector Algorithm (2) Must be made Stiffness Orthogonal to All Previously Calculated Vectors By the Modified Gram-Schmidt Algorithm If a Vector Is the Same As a Previously Calculated Vector It Must Be Rejected

The Natural Eigenvector Algorithm (3) A Static Vector Has A Zero Eigenvalue And An Infinite Frequency

A Truncated Set of Natural Eigenvalues Contains Linear Combinations of the Dynamic and Static Eigen Vectors That Are Excited by the Loading Therefore, They Are a Set of Load Dependent Ritz Vectors

Error Estimation 1. Dynamic Load Participation Ratio 2. Static Load Participation Ratio Therefore, this allows the LDR Algorithm to Automatic Terminate Generation when Error Limits are Satisfied

The dynamic load participation ratio for load case Fj is defined as the ratio of the kinetic energy captured by the truncated set of vectors to the total kinetic energy. Or For earthquake loading, this is identical to the mass participation factor in the three different directions A minimum of 90 percent is recommended

The static load participation ratio for load case Fj is defined as the ratio of the strain energy captured by the truncated set of vectors to the total strain energy due to the static load vectors. Or, Always equal to 1. 0 for LDR vectors

FINAL REMARKS Existing Dynamic Analysis Technology allows us to design earthquake resistant structures economically. However, many engineers are using Static Pushover Analysis to approximate earthquake forces. Advances in Computational Aero and Fluid Dynamics are not being used by the Civil Engineering Profession to Design Safe Structures for wind and wave loads. Many engineers are still using approximate wind tunnel results to generate Static Wind Loads.

In a large earthquake the safest place to be is on the top of a high-rise building Over 25 Stories


COMPUTERS 1958 TO 2008 IBM 701 - Multi-Processors The Current Speed of a $1, 000 Personal Computer is 1, 500 Times Faster than the $10, 000 Cray Computer of 1975
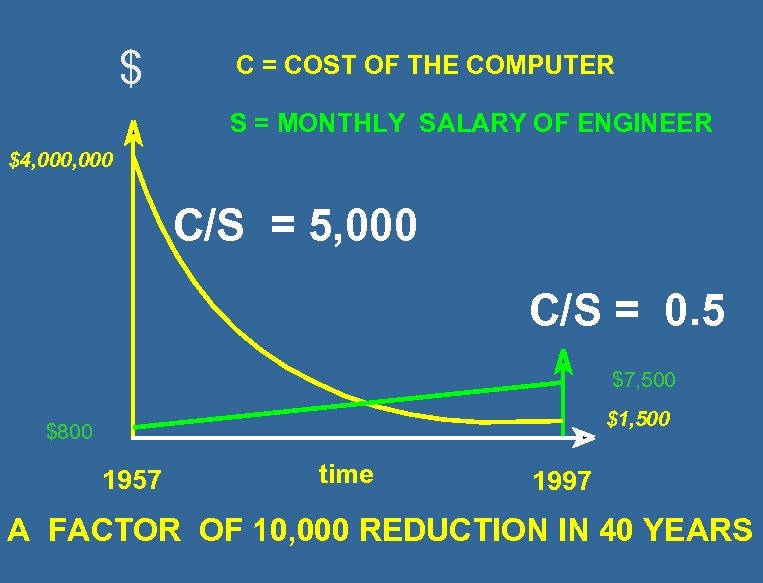
$ C = COST OF THE COMPUTER S = MONTHLY SALARY OF ENGINEER $4, 000 C/S = 5, 000 C/S = 0. 5 $7, 500 $1, 500 $800 1957 time 1997 A FACTOR OF 10, 000 REDUCTION IN 40 YEARS
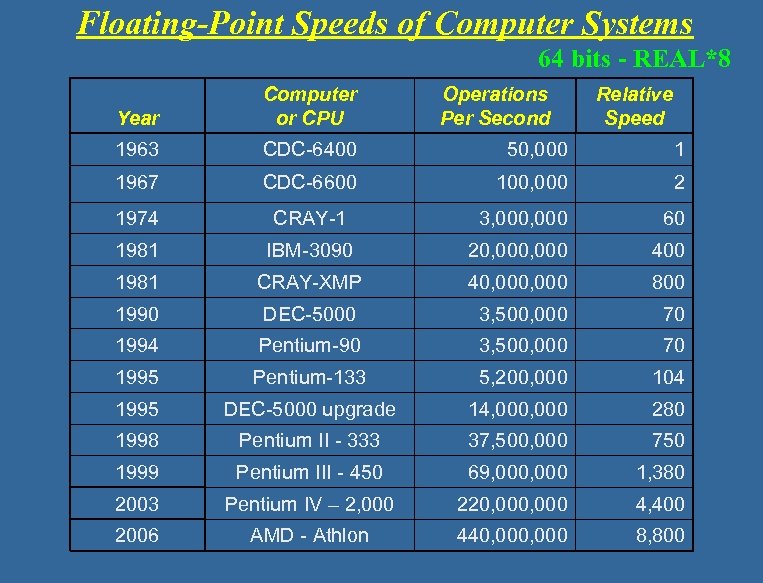
Floating-Point Speeds of Computer Systems Definition of one Operation A = B + C*D 64 bits - REAL*8 Year Computer or CPU Operations Per Second Relative Speed 1963 CDC-6400 50, 000 1 1967 CDC-6600 100, 000 2 1974 CRAY-1 3, 000 60 1981 IBM-3090 20, 000 400 1981 CRAY-XMP 40, 000 800 1990 DEC-5000 3, 500, 000 70 1994 Pentium-90 3, 500, 000 70 1995 Pentium-133 5, 200, 000 104 1995 DEC-5000 upgrade 14, 000 280 1998 Pentium II - 333 37, 500, 000 750 1999 Pentium III - 450 69, 000 1, 380 2003 Pentium IV – 2, 000 220, 000 4, 400 2006 AMD - Athlon 440, 000 8, 800
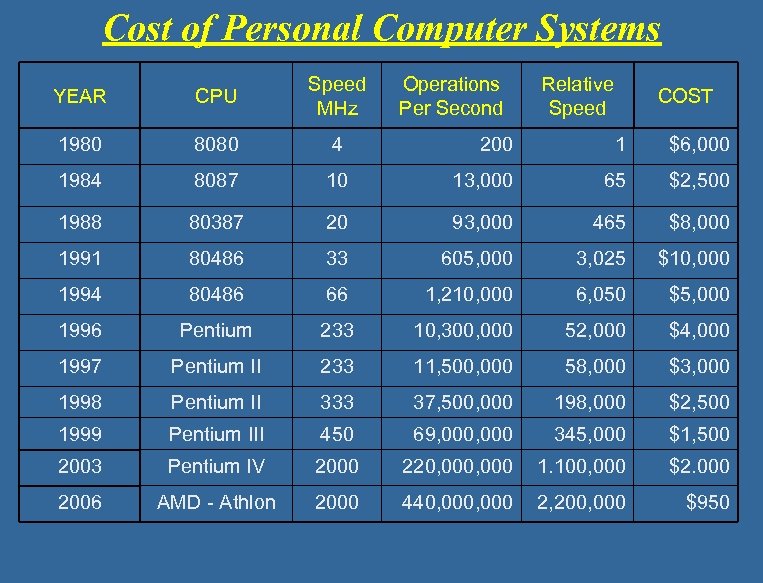
Cost of Personal Computer Systems YEAR CPU Speed MHz Operations Per Second Relative Speed 1980 8080 4 200 1 $6, 000 1984 8087 10 13, 000 65 $2, 500 1988 80387 20 93, 000 465 $8, 000 1991 80486 33 605, 000 3, 025 $10, 000 1994 80486 66 1, 210, 000 6, 050 $5, 000 1996 Pentium 233 10, 300, 000 52, 000 $4, 000 1997 Pentium II 233 11, 500, 000 58, 000 $3, 000 1998 Pentium II 333 37, 500, 000 198, 000 $2, 500 1999 Pentium III 450 69, 000 345, 000 $1, 500 2003 Pentium IV 2000 220, 000 1. 100, 000 $2. 000 2006 AMD - Athlon 2000 440, 000 2, 200, 000 $950 COST

Ed Wilson at UCLA Meet April 17, 1954 President Robert. Sproul Ed set a 880 yard record of 1 Minute and 54 Seconds. In the last 50 years, Ed is getting Slower and Computer are getting Faster

The Future Of Personal Computers Multi-Processors Will Require New Numerical Methods and Modification of Existing Programs Speed and Accuracy are Important
b576386b9002428049901e84e450867d.ppt