EART 162 PLANETARY INTERIORS Last Week

EART 162: PLANETARY INTERIORS

Last Week • Gravity and the potential • Bulk density inferred from gravity

This Week – Shapes and Moments of Inertia • Gravity gives us the mass/density of a planet. How? • Why is this useful? Density provides constraints on interior structure • What is the gross structure of a spinning planet? • We can obtain further constraints on the interior structure from the moment of inertia – How do we obtain it? – What does it tell us? • We can also use gravity to investigate lateral variations in the subsurface density • See Turcotte and Schubert chapter 5

What is the shape of a spinning planet? • Why do we care? f = (a-c)/a – f(internal structure, strength) • Spinning produces large topography relative to Earth’s geologic topography. • As the largest deformation, it’s an important reference point for all gravity and topography measurements. – Example: Satellite motions. • So what is the shape in equilibrium with gravity? Steel vs. water planet? Newton/ Late 1600 s.

Newton’s Method for Shape • The pressure under each water well (or column of mass) at the pole and equator must be equal, if the sphere is in equilibrium. • g varies with distance differently in each well. f = (a-c)/a c a a

Spinning Water Balloon Demonstration • Problems with comparing this to planets?

Reference Ellipsoid • A longitude-independent ellipsoid that serves as a reference for the shape of a planet (e. g. WGS 84 for the Earth). – Defined by a = 6, 378. 137 km at the equator and f = 1/298. 257223563.

Back to potentials • Recall: – Gravity potential extends out to infinity. – Obeys Laplace’s equation. – Its negative gradient is gravity. • Equipotential surfaces help define undulations in gravity (drawing of spherical potential with mountain perturbation) • Oceans form an equipotential surface.

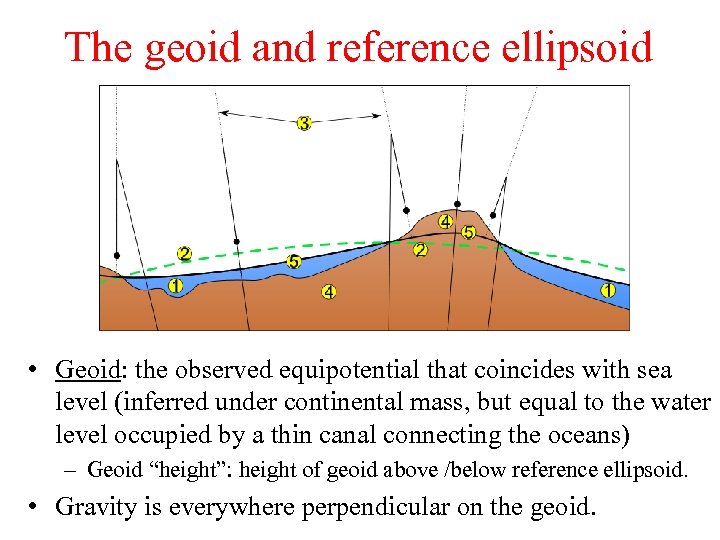The geoid and reference ellipsoid • Geoid: the observed equipotential that coincides with sea level (inferred under continental mass, but equal to the water level occupied by a thin canal connecting the oceans) – Geoid “height”: height of geoid above /below reference ellipsoid. • Gravity is everywhere perpendicular on the geoid.

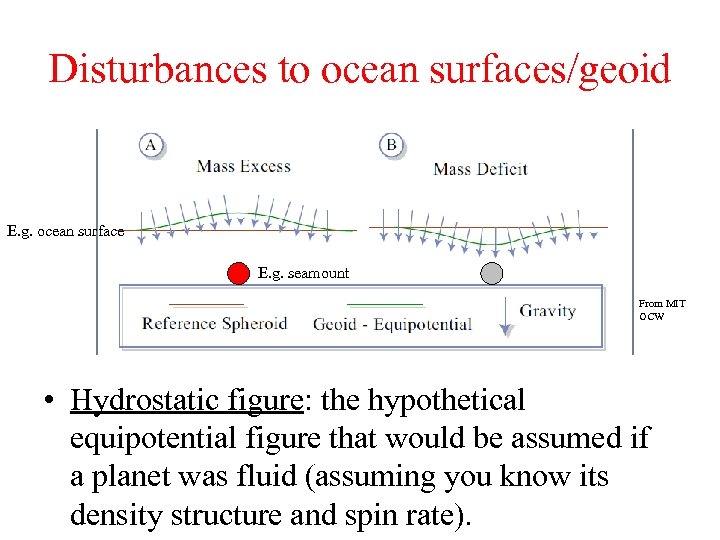Disturbances to ocean surfaces/geoid E. g. ocean surface E. g. seamount From MIT OCW • Hydrostatic figure: the hypothetical equipotential figure that would be assumed if a planet was fluid (assuming you know its density structure and spin rate).

Moments of Inertia • Gravity tells you about the density distribution, non-uniquely • Moments of inertia tell you about the radial distribution of density (also non-uniquely).

Moment of Inertia (1) • The moment of inertia (Mo. I) is a measure of an object’s resistance to being “spun up” or “spun down” • In many ways analogous to mass, but for rotation • Mo. I must always be measured about a particular axis (the axis of rotation) • The Mo. I is governed by the distribution of mass about this axis (mass further away = larger Mo. I) • Often abbreviated as I; also A, B, C for planets • In the absence of external forces (torques), angular momentum (Iw) is conserved (ice-skater example) R F w Linear acceleration: F Rotational acceleration: (T is torque (=2 F R))

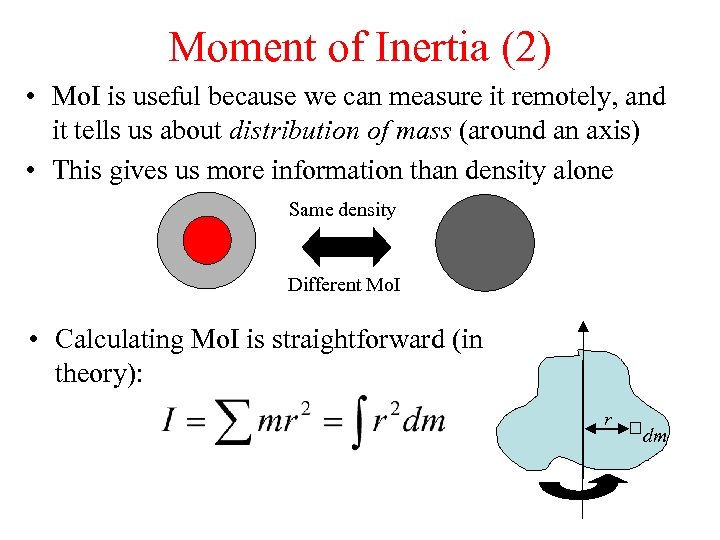Moment of Inertia (2) • Mo. I is useful because we can measure it remotely, and it tells us about distribution of mass (around an axis) • This gives us more information than density alone Same density Different Mo. I • Calculating Mo. I is straightforward (in theory): r dm

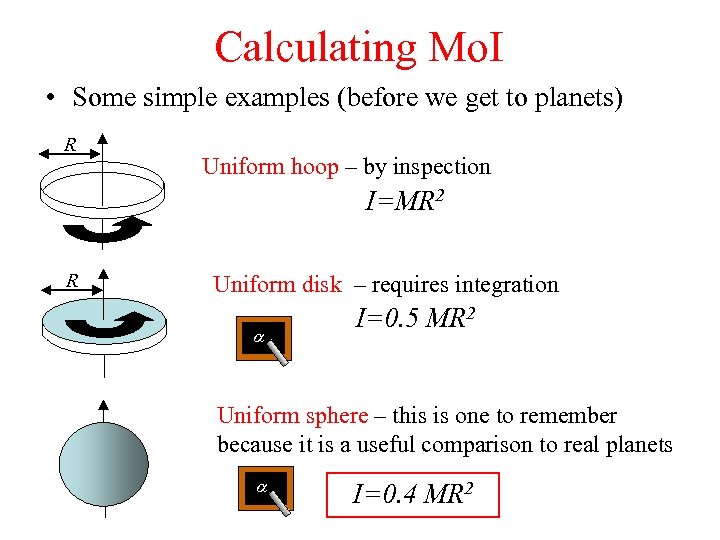Calculating Mo. I • Some simple examples (before we get to planets) R Uniform hoop – by inspection I=MR 2 R Uniform disk – requires integration a I=0. 5 MR 2 Uniform sphere – this is one to remember because it is a useful comparison to real planets a I=0. 4 MR 2

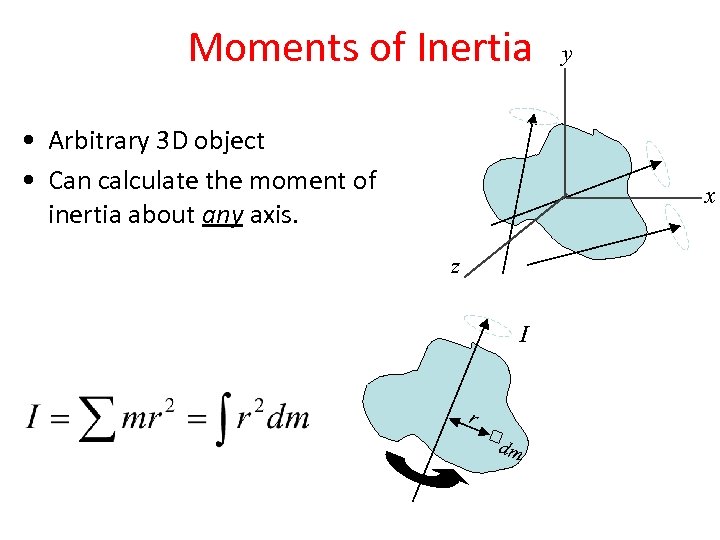Moments of Inertia • Arbitrary 3 D object • Can calculate the moment of inertia about any axis. y x z I r dm

Define the inertia tensor y x z

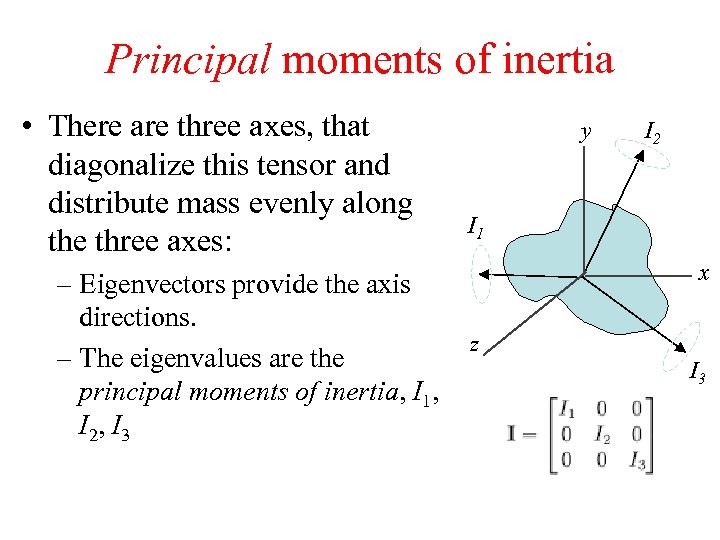Principal moments of inertia • There are three axes, that diagonalize this tensor and distribute mass evenly along the three axes: – Eigenvectors provide the axis directions. – The eigenvalues are the principal moments of inertia, I 1, I 2, I 3 y I 2 I 1 x z I 3

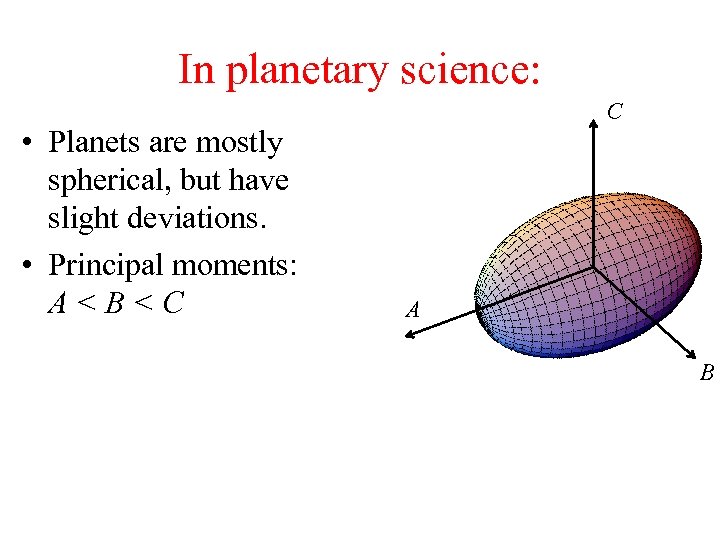In planetary science: • Planets are mostly spherical, but have slight deviations. • Principal moments: A

Aside: Relation to gravity spherical harmonics • Principal moments of inertia are related to the 2 -degree gravity spherical harmonics coefficients (r radius, M mass):

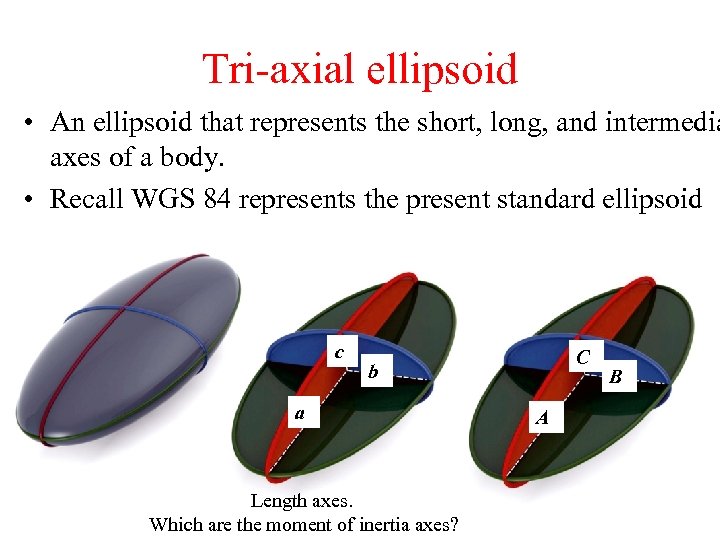Tri-axial ellipsoid • An ellipsoid that represents the short, long, and intermedia axes of a body. • Recall WGS 84 represents the present standard ellipsoid c C b a Length axes. Which are the moment of inertia axes? A B

True Polar Wander • Changes in a spinning planet’s moments of inertia produce an orientation change known as “true polar wander. ” Spin axis does NOT change

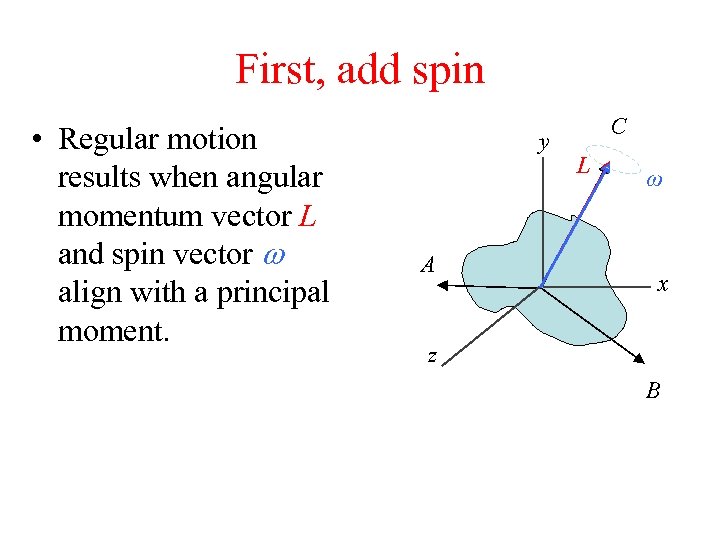First, add spin • Regular motion results when angular momentum vector L and spin vector w align with a principal moment. y A C L ω x z B

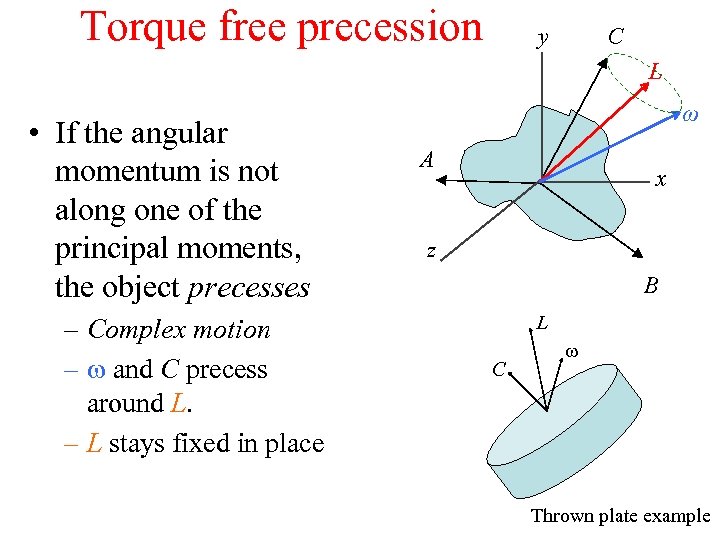Torque free precession C y L • If the angular momentum is not along one of the principal moments, the object precesses – Complex motion – w and C precess around L. – L stays fixed in place ω A x z B L C w Thrown plate example

Example 1: Toutatis • Rotation is not along a principal axis, free precession. • Damping to principal axis rotation? Chang’e 2 lunar mission (Dec. 2012)

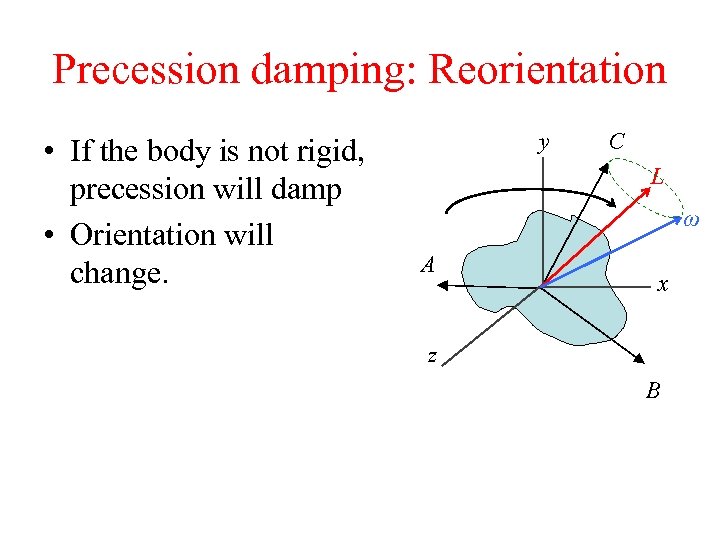Precession damping: Reorientation • If the body is not rigid, precession will damp • Orientation will change. y C L ω A x z B

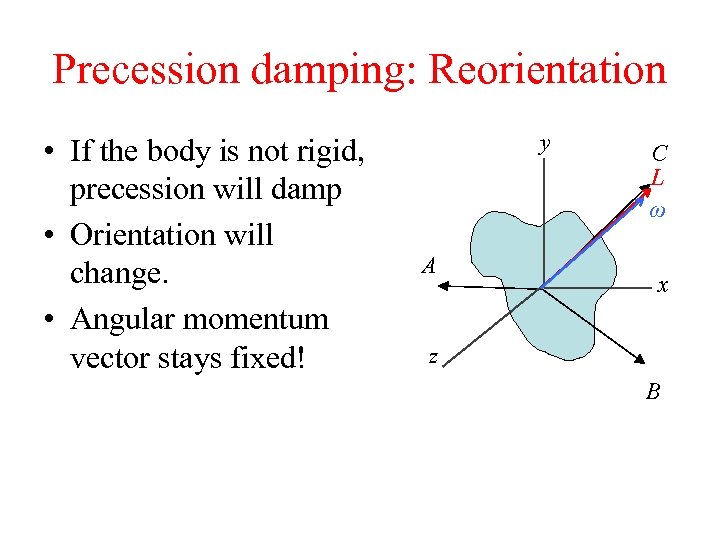Precession damping: Reorientation • If the body is not rigid, precession will damp • Orientation will change. • Angular momentum vector stays fixed! y A C L ω x z B

Aside: Damping timescale • Time to damp out precession in a non-rigid body – Depends on Q (quality factor) of the whole-body oscillations. – m is bulk rigidity (similar to Young’s modulus) – K 3 is ratio of average to maximum strain (~0. 010. 1) See Burns and Safronov 1973

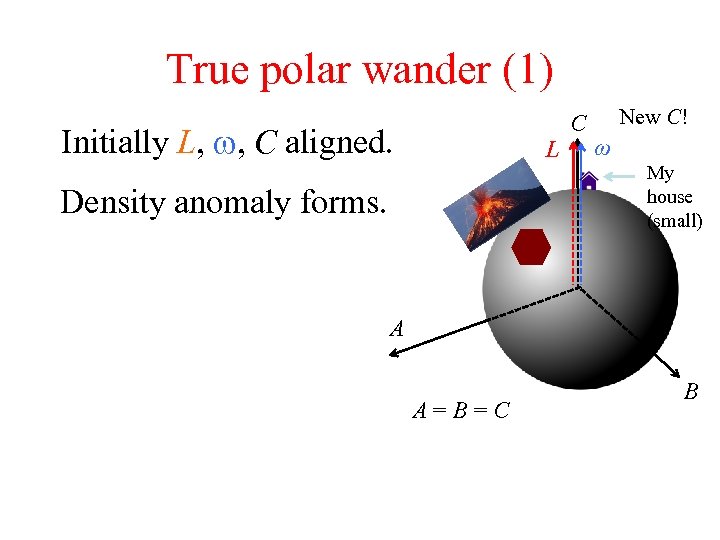True polar wander (1) Initially L, w, C aligned. L Density anomaly forms. C New C! ω My house (small) A A=B=C B

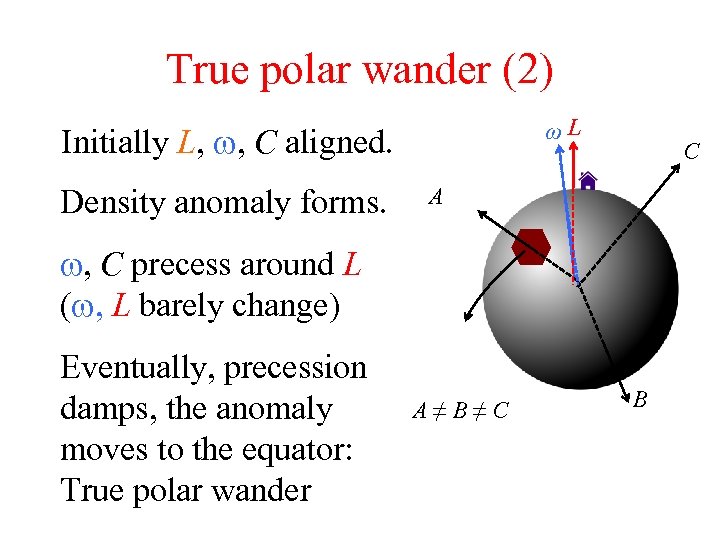True polar wander (2) ωL Initially L, w, C aligned. Density anomaly forms. C A w, C precess around L (w, L barely change) Eventually, precession damps, the anomaly moves to the equator: True polar wander A≠B≠C B

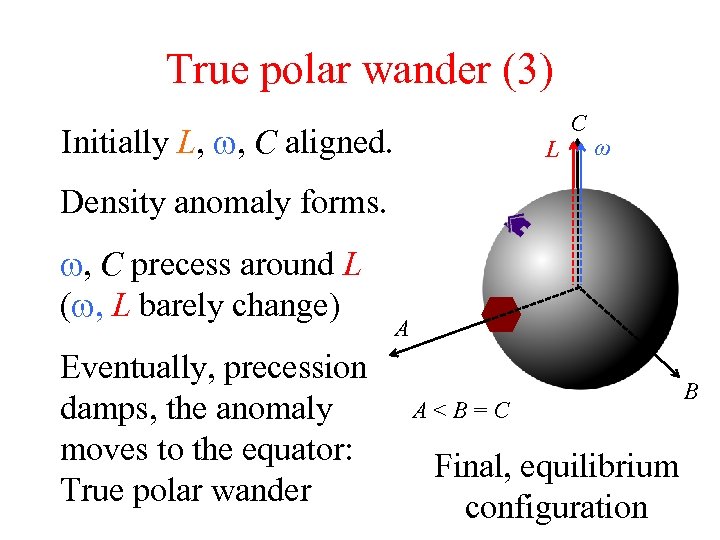True polar wander (3) Initially L, w, C aligned. L C ω Density anomaly forms. w, C precess around L (w, L barely change) Eventually, precession damps, the anomaly moves to the equator: True polar wander A A

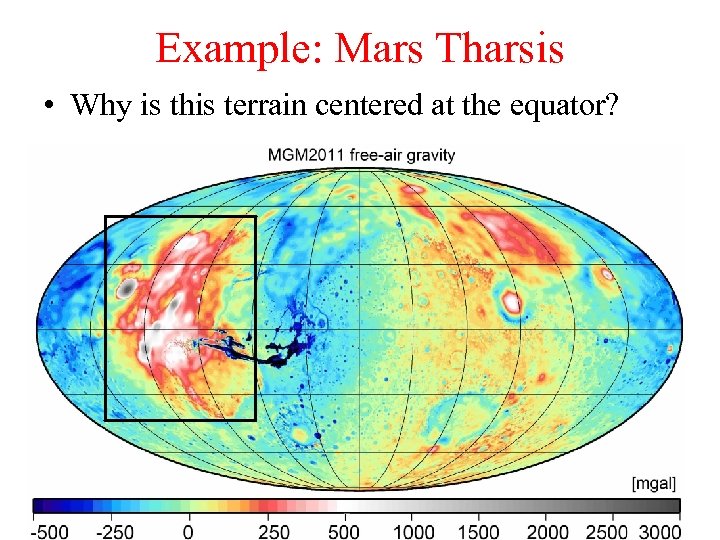Example: Mars Tharsis • Why is this terrain centered at the equator?

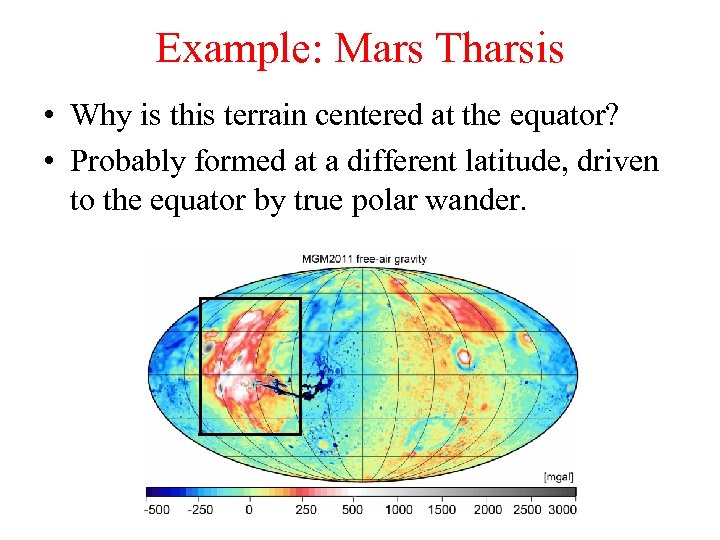Example: Mars Tharsis • Why is this terrain centered at the equator? • Probably formed at a different latitude, driven to the equator by true polar wander.

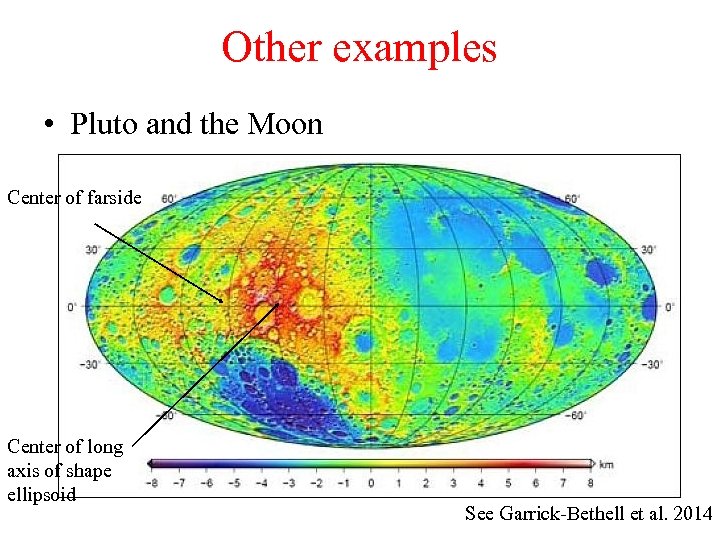Other examples • Pluto and the Moon Center of farside Center of long axis of shape ellipsoid See Garrick-Bethell et al. 2014

Other examples • Pluto and the Moon Nimmo et al. 2016

Torque-free precession (summary) L • Precession: rotation of the rotation axis, about some other axis. • Rotation about a principal axis of inertia is stable. – Angular velocity vector (w) and angular momentum (L = Iw) vectors will be aligned. n w • If misaligned: – Torque-free precession. Precession of w (and n in the same plane) about L. Example: thrown plate/spinning disk. – If the body is at least semi-fluid, it will slowly rearrange to align the two (principal axis rotation), possibly over millions of years for planetary bodies. – Example: Lunar polar wander. Asteroid Toutatis is in a state of free precession

True polar wander (summary) • Moment of inertia changes happen (geology) misaligns C and L. • C prefers energetically to align with L, and does so over long times if the body is semi-fluid. • Hence, the planet’s orientation changes, while L stays fixed in space. Red blob represents a positive density anomaly that just appeared. It shifts the C moment axis away from the spin axis. Eventually Earth shifts the mass to the equator, realigning C and L.

Moments of inertia + gravity • Planets are flattened (because of rotation - centripetal) • This means that their moments of inertia (A, B, C) are different. By convention C>B>A • C is usually the moment about the axis of rotation C A • Differences in moments of inertia are indications of how much excess mass is concentrated along which axes, example: (C-A) represents how much mass is in the equator. Related to the flattening f = (a-c)/a.

Moment of Inertia Difference • Because a moment of inertia difference indicates an excess in mass at the equator, there will also be a corresponding effect on the gravity field • So we can use observations of the gravity field to infer the moment of inertia difference • The effect on the gravity field will be a function of position (+ at equator, - at poles) Mass deficit at poles Mass excess at equator How do we use the gravity to infer the moment of inertia difference?

Relating C-A to gravity (1) • Here is a simple example which gives a result comparable to the full solution • See T&S Section 5. 2 for the full solution (tedious) P M b r a f R Point source: m/2 We represent the equatorial bulge as two extra blobs of material, each of mass m/2, added to a body of mass M. We can calculate the resulting Mo. I difference and effect on the gravitational acceleration as a function of latitude f. Extra term from bulge: Corresponding increase in C : m. R 2 increase in A: 0 So now we have a description of the gravity field of a flattened body, and its Mo. I difference (C-A = m. R 2)

Gravity field of a flattened planet • The full solution is called Mac. Cullagh’s formula: Point source Contribution from bulge Mo. I difference • Note the similarities to the simplified form derived on the previous page • So we can use a satellite to measure the gravity field as a function of distance r and latitude f, and obtain C-A • We’ll discuss how to get C from C-A in a while • The Mo. I difference is often described by J 2, where J 2 is dimensionless, a is the equatorial radius. This is a the second degree spherical harmonic coefficient, with l = 2, m = 0, can be written C 2, 0

Examples • MESSENGER mission to Mercury: Early flyby produced C-A estimates. • MESSENGER mission goal was to improve these estimates via the second degree spherical harmonics (J 2) • C-A estimates can tell us about the strength and internal structure of a body: is the flattening equal to the hydrostatic value (more later)?

Effect of rotation (on surface) • Final complication – a body on the surface of the planet experiences rotation and thus a centrifugal acceleration • Effect is pretty straightforward: w r cosf r f Radial component of acceleration: Outwards acceleration where w is the angular velocity So the complete formula for acceleration g on a planet surface is:

Recall: Gravitational Potential • Gravitational potential is the work done to bring a unit mass from infinity to the point in question: • For a spherically symmetric body, U=-GM/r • For a rotationally flattened planet, we end up with: • This is useful because a fluid will have the same potential everywhere on its surface – so we can predict the shape of a rotating fluid body

Rotating Fluid Body Shape • For a fluid, the grav. potential is the same everywhere on the surface • Let’s equate the polar and equatorial potentials for our rotating shape, and let us also define the ellipticity a (or flattening): c • After a bit of algebra, we end up with: Note approximate! a Remember that this only works for a fluid body! • Does this make sense? • Why is this expression useful? • Is it reasonable to assume a fluid body?

Pause & Summary • Moment of inertia depends on distribution of mass • For planets, C>A because mass is concentrated at the equator as a result of the rotational bulge • The gravity field is affected by the rotational bulge, and thus depends on C-A (or, equivalently, J 2) • So we can measure C-A remotely (e. g. by observing a satellite’s orbit) • If the body has no elastic strength, we can also predict the shape of the body given C-A (or we can infer C-A by measuring the shape)

How do we get C from C-A? • Recall that we can use observations of the gravity field to obtain a body’s Mo. I difference C-A • But what we would really like to know is the actual moment of inertia, C (why? ) • Two possible approaches: – Observations of precession of the body’s axis of rotation – Assume the body is fluid (hydrostatic) and use theory

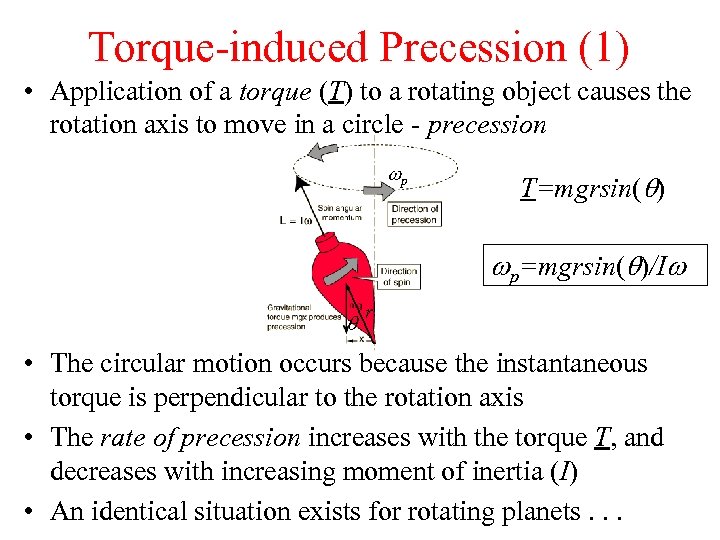Torque-induced Precession (1) • Application of a torque (T) to a rotating object causes the rotation axis to move in a circle - precession wp T=mgrsin( ) wp=mgrsin( )/Iw r • The circular motion occurs because the instantaneous torque is perpendicular to the rotation axis • The rate of precession increases with the torque T, and decreases with increasing moment of inertia (I) • An identical situation exists for rotating planets. . .

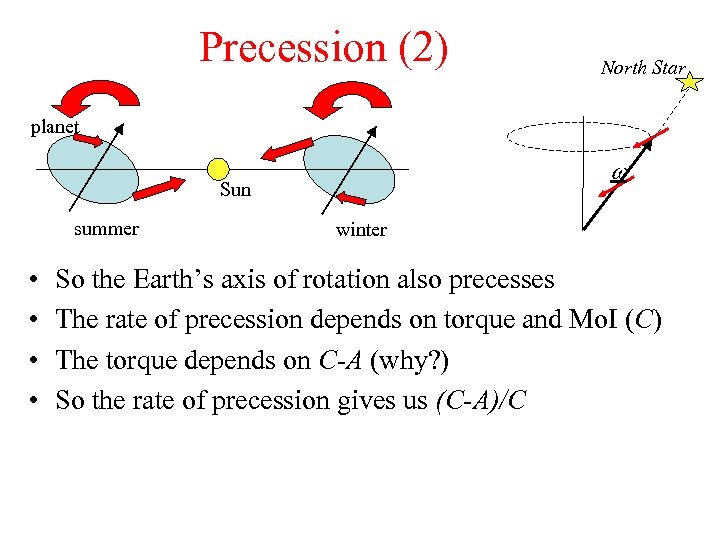Precession (2) North Star planet w Sun summer • • winter So the Earth’s axis of rotation also precesses The rate of precession depends on torque and Mo. I (C) The torque depends on C-A (why? ) So the rate of precession gives us (C-A)/C

Putting it together • If we can measure the rate of precession of the rotation axis, we get (C-A)/C • For which bodies do we know the precession rate? • Given the planet’s gravitational field, or its flattening, we can deduce J 2 (or equivalently C-A) • Given (C-A)/C and (C-A), we can deduce C • Why is this useful? • What do we do if we can’t measure the precession rate?

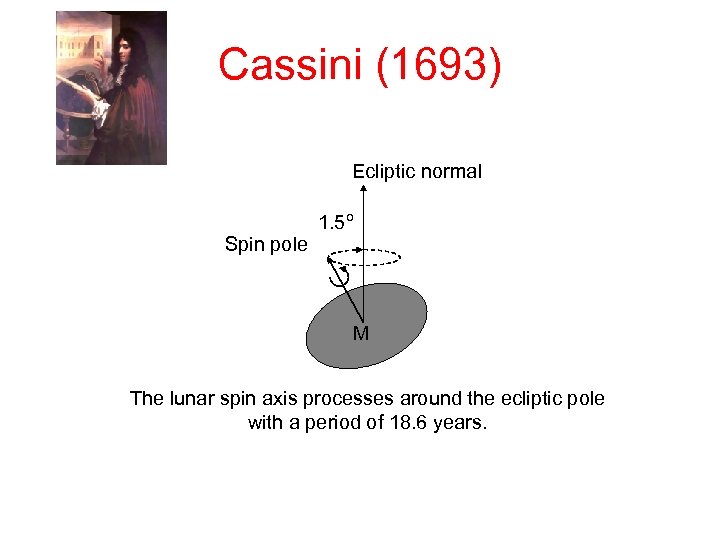Cassini (1693) Ecliptic normal 1. 5º Spin pole M The lunar spin axis processes around the ecliptic pole with a period of 18. 6 years.

Laplace (1799) • The precession of the lunar spin is due to torques from the Earth on an oblate Moon. • The spin axis precession rate implies a certain magnitude of oblateness = C-A. Ecliptic normal Spin pole Force E Calculated (C-A)/A M Force C A M Moon

Laplace (1799) C • Also calculated predicted present value from spin. • Concluded the Moon is not in hydrostatic equilibrium with the predicted figure. • (C-A)/A is at least 20 times too high. M A Moon observed (C-A)/A = 6 x 10 -4 C A M (C-A)/A < 3 x 10 -5 Hydrostatic predicted

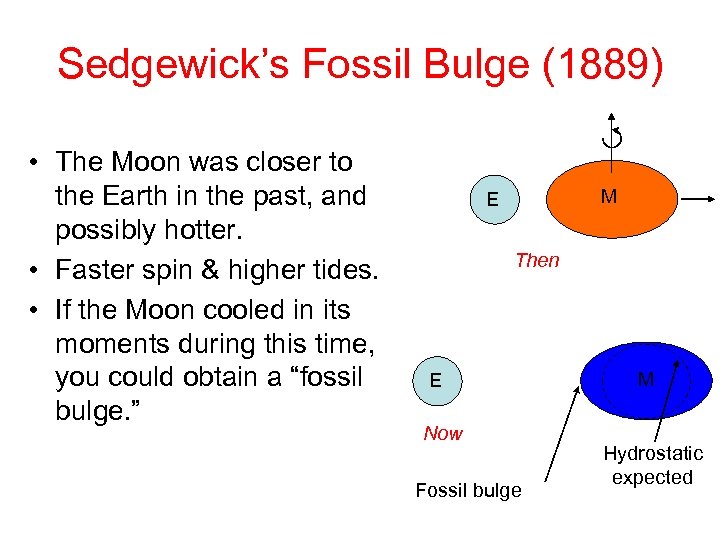Sedgewick’s Fossil Bulge (1889) • The Moon was closer to the Earth in the past, and possibly hotter. • Faster spin & higher tides. • If the Moon cooled in its moments during this time, you could obtain a “fossil bulge. ” M E Then E Now Fossil bulge M Hydrostatic expected

Hydrostatic assumption • In most cases, the precession rate of the planet is not available. How do we then derive C? • If we assume that the planet is hydrostatic (i. e. it has no elastic strength), then we can derive C directly from C-A using the Darwin-Radau approximation*: Here the flattening depends on C. We also have an equation giving f in terms of C-A (see before) • This tells us the flattening expected for a fluid rotating body with a non-uniform density distribution • Depends on C! Does this equation make sense? * I’m not going to derive this; see C. R. Acad. Sci. Paris 100, 972 -974, 1885 and Mon. Not. R. Astron. Soc. 60 82 -124 1899

Earth as an example • We can measure J 2 and thus calculate f (assuming a fluid Earth): J 2=1. 08 x 10 -3 , w 2 a 3/GM=3. 47 x 10 -3 f=(3/2)J 2 + w 2 a 3/2 GM f=3. 36 x 10 -3 • The observed flattening f=3. 35 x 10 -3. Comments? • A fluid Earth is a good assumption, so we can use f and the Darwin-Radau relation to obtain C/Ma 2 • We get an answer of C/Ma 2=0. 331. The real value is 0. 3308. a • What do we conclude? • Next: what use is knowing C/Ma 2, anyway?

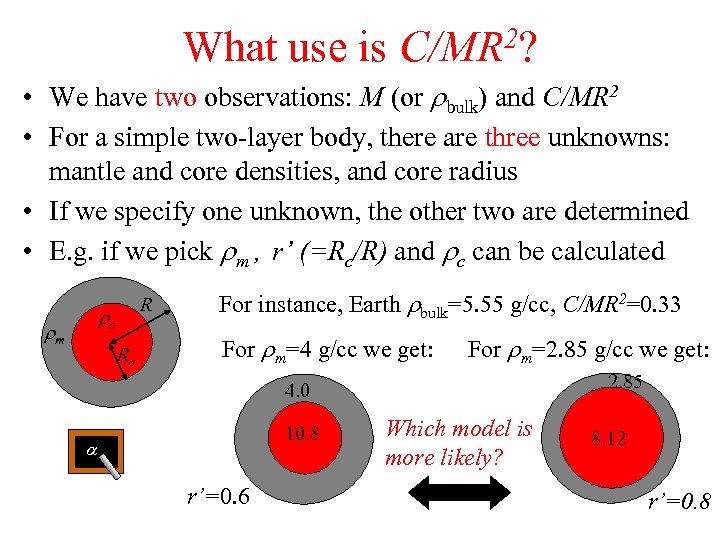What use is 2? C/MR • We have two observations: M (or rbulk) and C/MR 2 • For a simple two-layer body, there are three unknowns: mantle and core densities, and core radius • If we specify one unknown, the other two are determined • E. g. if we pick rm , r’ (=Rc/R) and rc can be calculated R rc rm Rc For instance, Earth rbulk=5. 55 g/cc, C/MR 2=0. 33 For rm=4 g/cc we get: For rm=2. 85 g/cc we get: 2. 85 4. 0 10. 8 a r’=0. 6 Which model is more likely? 8. 12 r’=0. 8

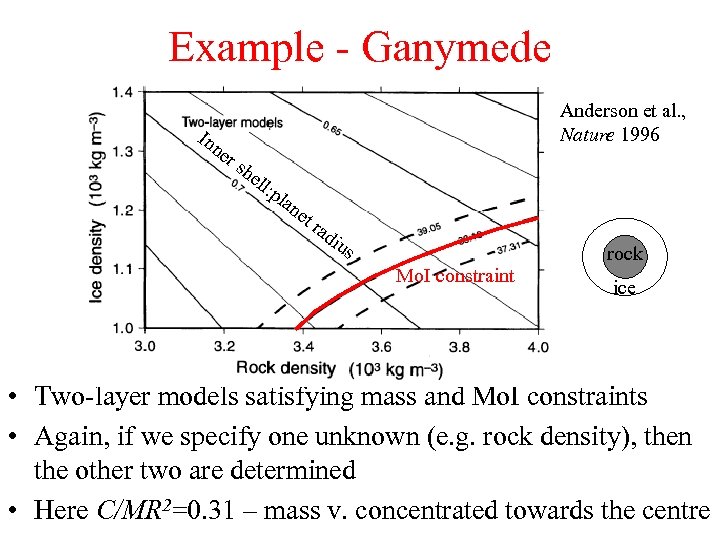Example - Ganymede In ne rs Anderson et al. , Nature 1996 he ll: pla ne t rad ius Mo. I constraint rock ice • Two-layer models satisfying mass and Mo. I constraints • Again, if we specify one unknown (e. g. rock density), then the other two are determined • Here C/MR 2=0. 31 – mass v. concentrated towards the centre

Another example: Mercury • (C-A)/C was measured with precise radar observations of the surface from Earth before MESSENGER – Crude J 2 estimates from Mariner 10 were used to crudely constrain C. • J 2 was measured with MESSENGER spacecraft. Combine with radar-based spin observations! • Result: C/MR 2 = 0. 346 0. 014. • See 2012 paper posted online

Pause & Summary • Measuring the gravity field gives us J 2 (or C-A) • To get the internal structure, we need C • Two options: – 1) Measure the precession rate of the rotation axis of the body (via lander tracking or radar measurements). The precession rate depends on (C-A)/C, so we can deduce C (if we know J 2) – 2) Or, assume that the body is hydrostatic. This allows us to deduce C directly from C-A (J 2 ) • We normally express C as C/MR 2, for comparison with a uniform sphere (C/MR 2=0. 4) • Most bodies have C/MR 2 < 0. 4, indicating a concentration of mass towards their centres (differentiation)

Local gravity variations (1) • So far we have talked about using planet-scale variations in gravity to infer bulk structure • We can also use more local observations of gravity to make inferences about local subsurface structure • How do we make such local observations? gravimeter Earth Radio Doppler shift gives line-of-sight acceleration • Local gravity anomalies are typically small, so we use units of milli. Gals (m. Gal). 1 m. Gal=10 -5 ms-2~10 -6 g. Earth

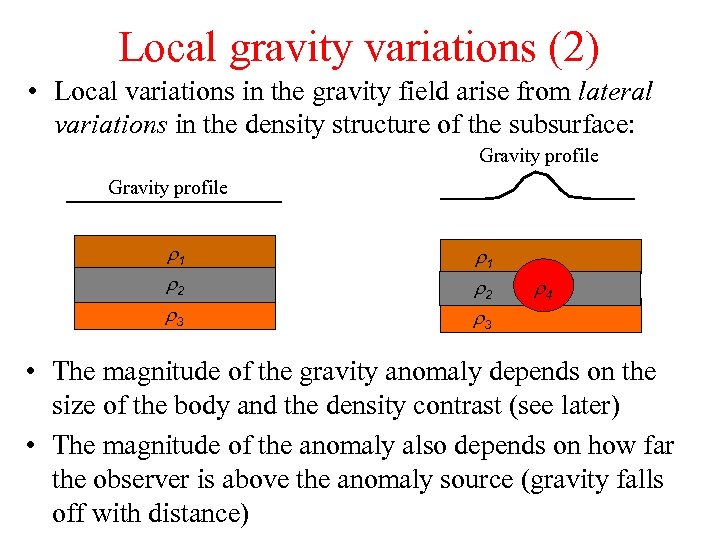Local gravity variations (2) • Local variations in the gravity field arise from lateral variations in the density structure of the subsurface: Gravity profile r 1 r 2 r 3 r 4 • The magnitude of the gravity anomaly depends on the size of the body and the density contrast (see later) • The magnitude of the anomaly also depends on how far the observer is above the anomaly source (gravity falls off with distance)

Free Air Gravity • When making ground-based observations, we reference measurements to our reference spheroid (e. g. latitudedependent changes due to rotation, Mac. Cullagh’s formula) • We also have to correct for the fact that the local gravity we measure depends on our elevation (plus as any local density anomalies) • This correction is known as the free-air correction and gives us the gravity as if measured at a reference elevation • The free air correction Dg for an elevation h is given by a Here g 0 is the reference accleration due to gravity and R is the planetary radius This correction is only correct for h<

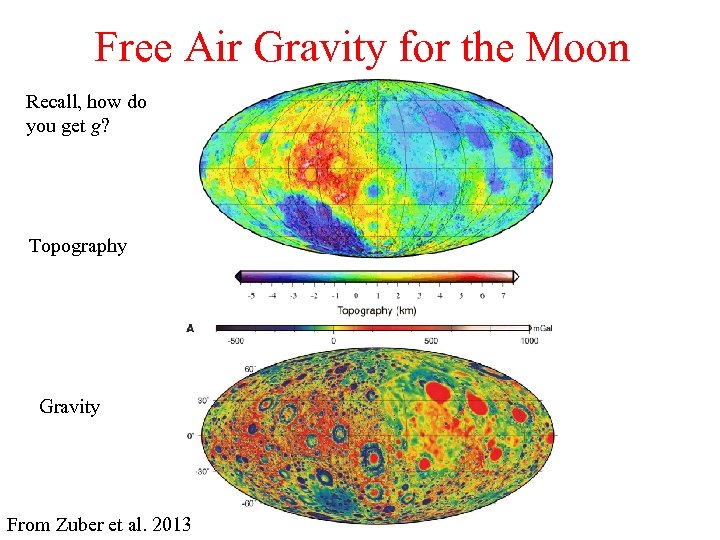Free Air Gravity for the Moon Recall, how do you get g? Topography Gravity From Zuber et al. 2013

Gravity due to a plate (Bouguer correction) Reference Dr z Observer h R • For an observer close to the center (z<

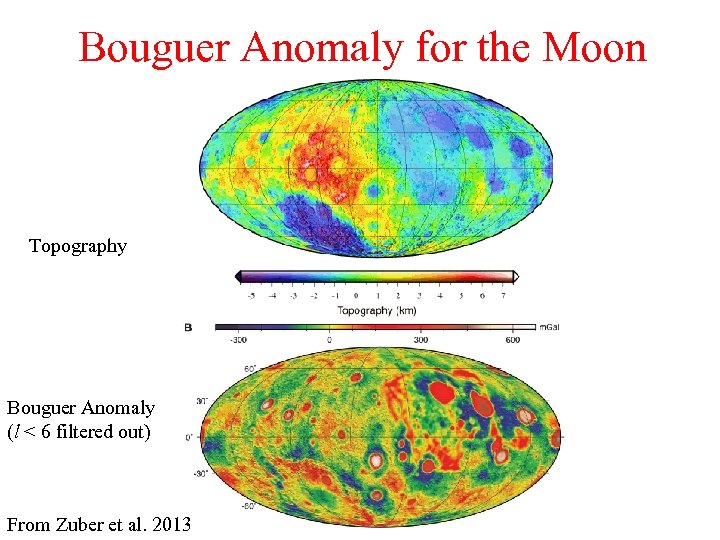Bouguer Anomaly for the Moon Topography Bouguer Anomaly (l < 6 filtered out) From Zuber et al. 2013

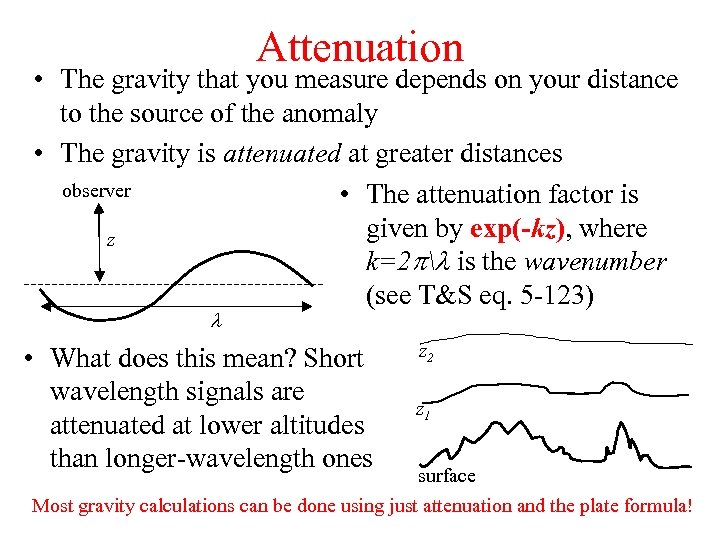Attenuation • The gravity that you measure depends on your distance to the source of the anomaly • The gravity is attenuated at greater distances observer • The attenuation factor is given by exp(-kz), where z k=2 pl is the wavenumber (see T&S eq. 5 -123) l • What does this mean? Short wavelength signals are attenuated at lower altitudes than longer-wavelength ones z 2 z 1 surface Most gravity calculations can be done using just attenuation and the plate formula!

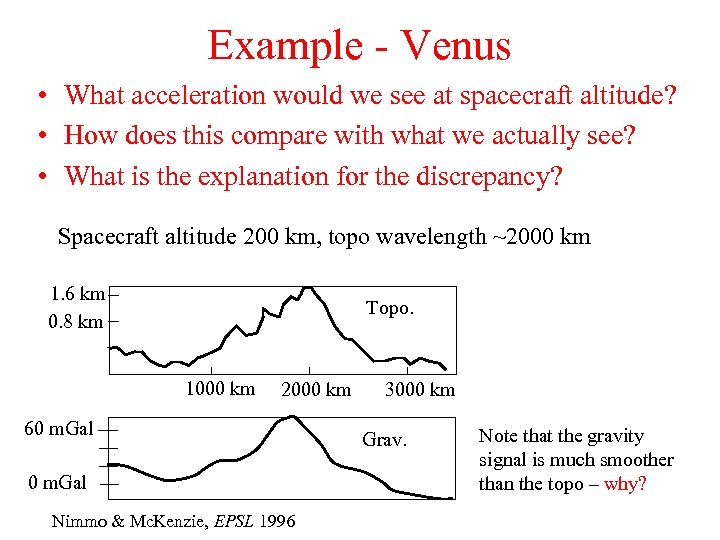Example - Venus • What acceleration would we see at spacecraft altitude? • How does this compare with what we actually see? • What is the explanation for the discrepancy? Spacecraft altitude 200 km, topo wavelength ~2000 km 1. 6 km 0. 8 km Topo. 1000 km 2000 km 60 m. Gal Nimmo & Mc. Kenzie, EPSL 1996 3000 km Grav. Note that the gravity signal is much smoother than the topo – why?

Titan Shape Paper Discussion • Iess et al. 2010. • 10 minutes

Summary • Global gravity variations arise due to Mo. I difference (J 2) • So we can measure J 2=C-A remotely • We can also determine C, either by observation or by making the hydrostatic assumption • Knowing C places an additional constraint on the internal structure of a planet (along with density) • Local gravity variations arise because of lateral differences in density structure • We can measure these variations by careful observation of a spacecraft’s orbit • The variations are attenuated upwards, depending on the observation altitude and wavelength

Key concepts/terms • • Gravity potential Principal moments of inertia C C-A, (C-A)/C Geoid Flattening Reference ellipsoid Hydrostatic figure