Джоза йя Уи ллард Гиббс 1839 1903 г

Зарегистрируйтесь, чтобы просмотреть полный документ!

Джоза йя Уи ллард Гиббс (1839— 1903 г. ) Американский физик, физикохимик, математик и механик, один из создателей векторного анализа, статистической физики, математической теории термодинамики, что во многом предопределило развитие современных точных наук и естествознания в целом.

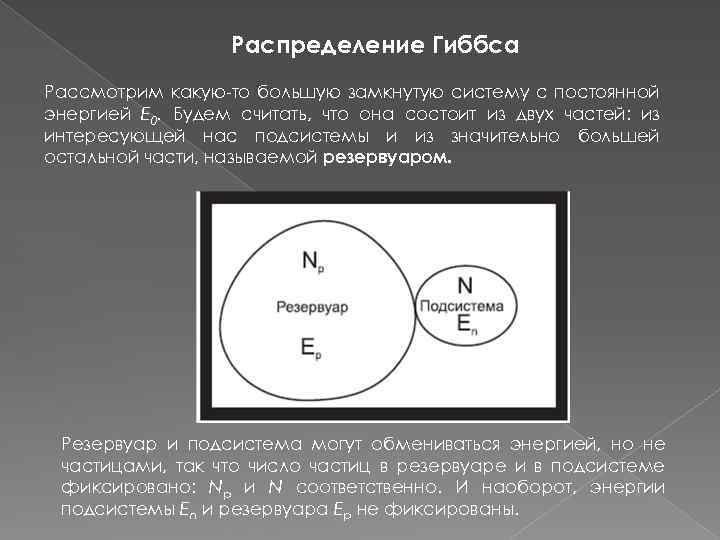
Распределение Гиббса Рассмотрим какую то большую замкнутую систему с постоянной энергией E 0. Будем считать, что она состоит из двух частей: из интересующей нас подсистемы и из значительно большей остальной части, называемой резервуаром. Резервуар и подсистема могут обмениваться энергией, но не частицами, так что число частиц в резервуаре и в подсистеме фиксировано: Nр и N соответственно. И наоборот, энергии подсистемы En и резервуара Eр не фиксированы.

В силу закона сохранения энергии Eр +En =E 0. (1) Мы ищем вероятность wn того, что при наблюдении в некоторый момент времени наша подсистема будет обнаружена в определенном квантовом состоянии n (каком либо одном) с энергией En. Очевидно, что эта вероятность пропорциональна числу допустимых состояний резервуара с энергией E 0 - En: wn ∼ g(Nр , Eр)=g(Nр , E 0 -En). (2)

Искомую вероятность можно разложить в ряд Тейлора по степеням En. Но в силу уже известного нам факта, что функция g(N, E) является чрезвычайно быстро растущей функцией энергии, рас кладывать в ряд Тейлора надо не саму вероятность wn, а ее логарифм: (3)

В результате мы приходим к следующей формуле для вероятности wn: (4) Распределение (4) называется распределением Гиббса, или каноническим распределением; оно было открыто Гиббсом для классической статистики в 1901 г. . Нормировочная постоянная A определяется условием (5)

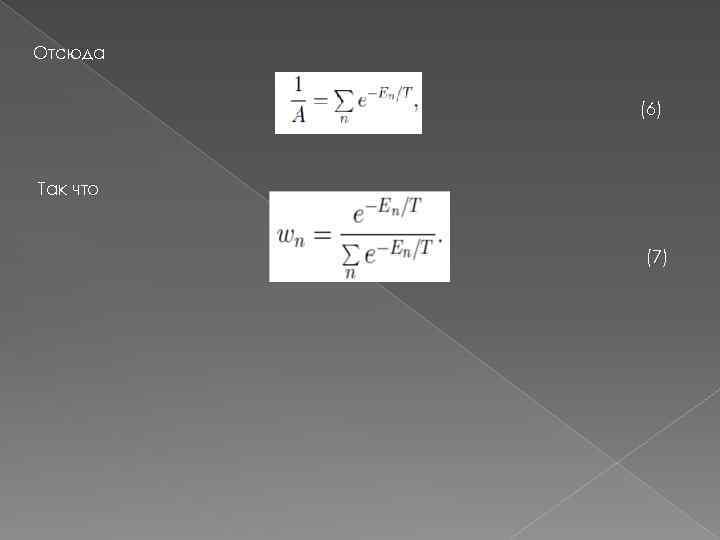
Отсюда (6) Так что (7)

В классической статистике распределение Гиббса имеет точно такой же вид, как в квантовой статистике, но для функции распределения в фазовом пространстве (8) где E(p, q) энергия тела как функция его координат и импульсов. Нормировочная постоянная определяется условием (9)

Скачать презентацию Джоза йя Уи ллард Гиббс 1839 1903 г

Распределение Гиббса.pptx

Количество слайдов: 7