Dynamics of Ions in an Electrostatic Ion Beam

Dynamics of Ions in an Electrostatic Ion Beam Trap Daniel Zajfman Dept. of Particle Physics Weizmann Institute of Science Israel and Max-Planck Institute for Nuclear Physics Heidelberg, Germany • Oded Heber • Henrik Pedersen ( MPI) • Michael Rappaport • Adi Diner • Daniel Strasser • Yinon Rudich • Irit Sagi • Sven Ring • Yoni Toker • Peter Witte (MPI) • Nissan Altstein • Daniel Savin (NY) Charles Coulomb (1736 -1806)

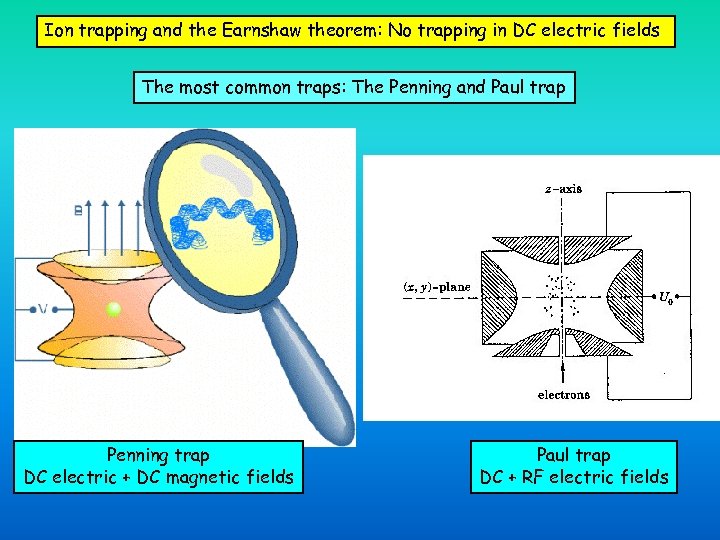
Ion trapping and the Earnshaw theorem: No trapping in DC electric fields The most common traps: The Penning and Paul trap Penning trap DC electric + DC magnetic fields Paul trap DC + RF electric fields

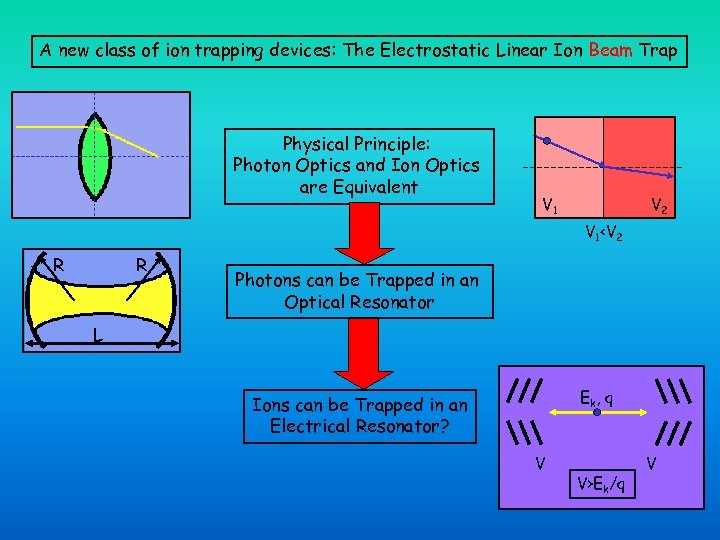
A new class of ion trapping devices: The Electrostatic Linear Ion Beam Trap Physical Principle: Photon Optics and Ion Optics are Equivalent V 1 V 2 V 1<V 2 R R Photons can be Trapped in an Optical Resonator L Ek , q Ions can be Trapped in an Electrical Resonator? V V>Ek/q V

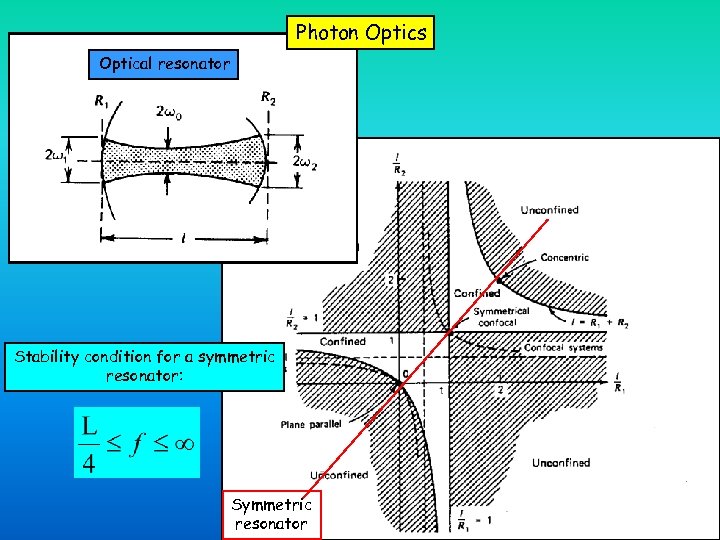
Photon Optics Optical resonator Stability condition for a symmetric resonator: Symmetric resonator

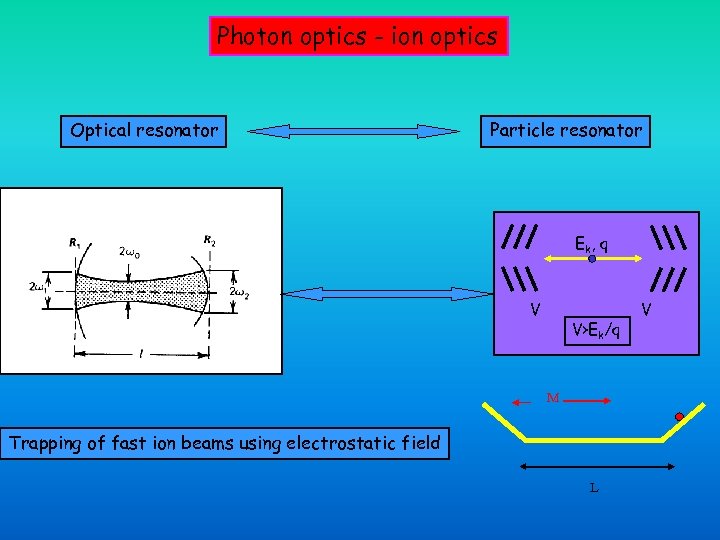
Photon optics - ion optics Optical resonator Particle resonator Ek , q V V>Ek/q M Trapping of fast ion beams using electrostatic field L V

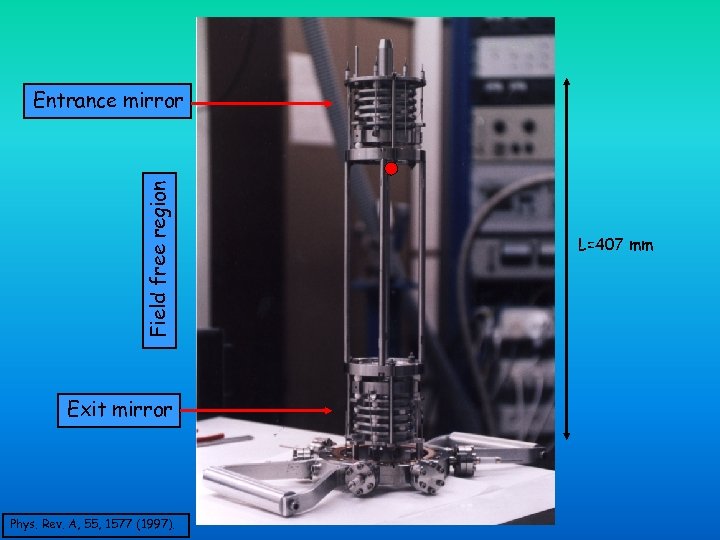
Field free region Entrance mirror Exit mirror Phys. Rev. A, 55, 1577 (1997). L=407 mm

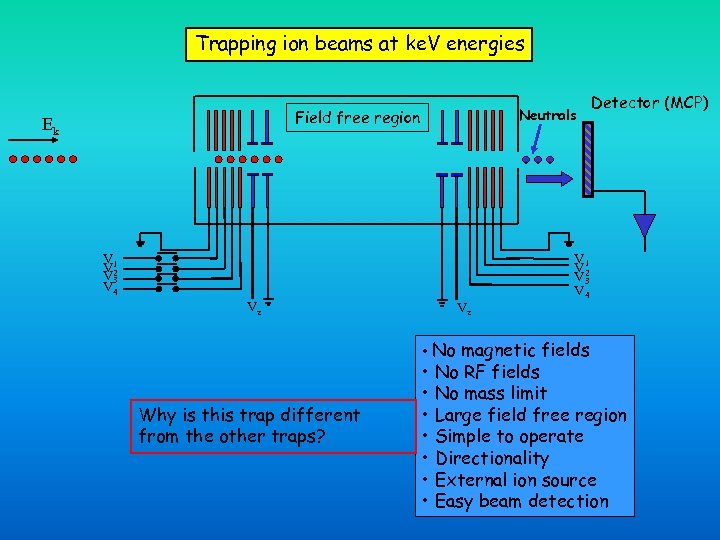
Trapping ion beams at ke. V energies Neutrals Field free region Ek V 1 V 2 V 3 V 4 Vz Vz V 1 V 2 V 3 V 4 • No magnetic fields Why is this trap different from the other traps? Detector (MCP) • No RF fields • No mass limit • Large field free region • Simple to operate • Directionality • External ion source • Easy beam detection

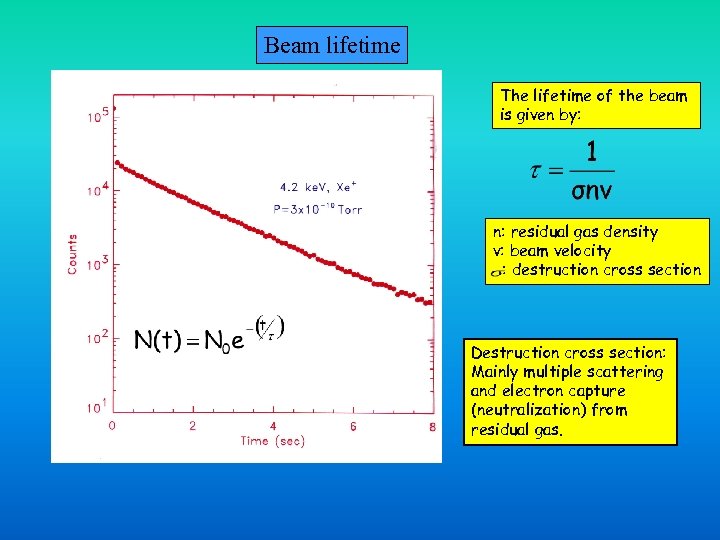
Beam lifetime The lifetime of the beam is given by: n: residual gas density v: beam velocity : destruction cross section Destruction cross section: Mainly multiple scattering and electron capture (neutralization) from residual gas.

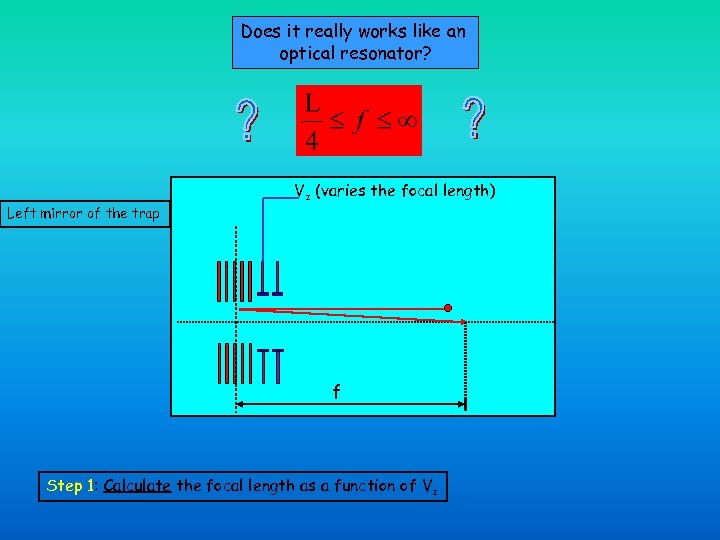
Does it really works like an optical resonator? Left mirror of the trap Vz (varies the focal length) f Step 1: Calculate the focal length as a function of Vz

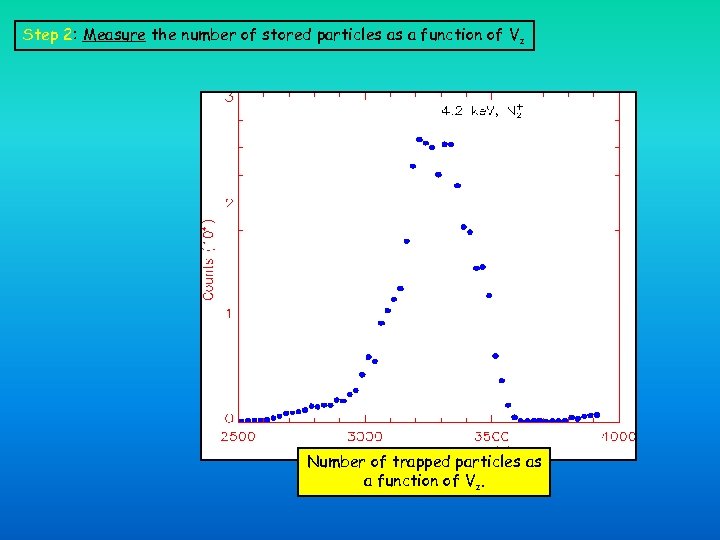
Step 2: Measure the number of stored particles as a function of Vz Number of trapped particles as a function of Vz.

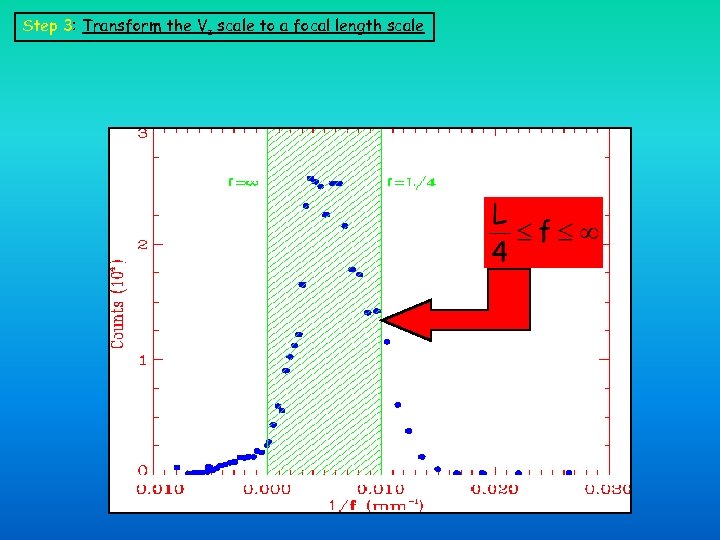
Step 3: Transform the Vz scale to a focal length scale

Physics with a Linear Electrostatic Ion Beam Trap • Cluster dynamics • Ion beam – time dependent laser spectroscopy • Laser cooling • Stochastic cooling • Metastable states • Radiative cooling • Electron-ion collisions • Trapping dynamics

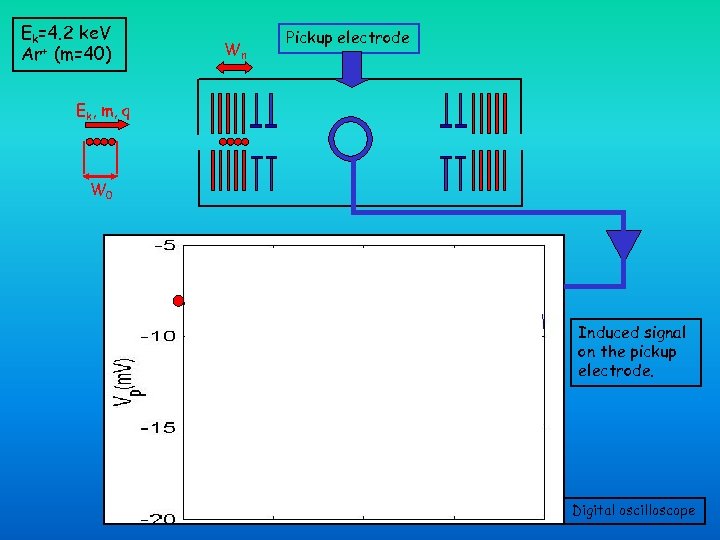
Ek=4. 2 ke. V Ar+ (m=40) Wn Pickup electrode Ek, m, q W 0 Induced signal on the pickup electrode. T 2930 ns (f=340 k. Hz) 2 Wn 280 ns Digital oscilloscope

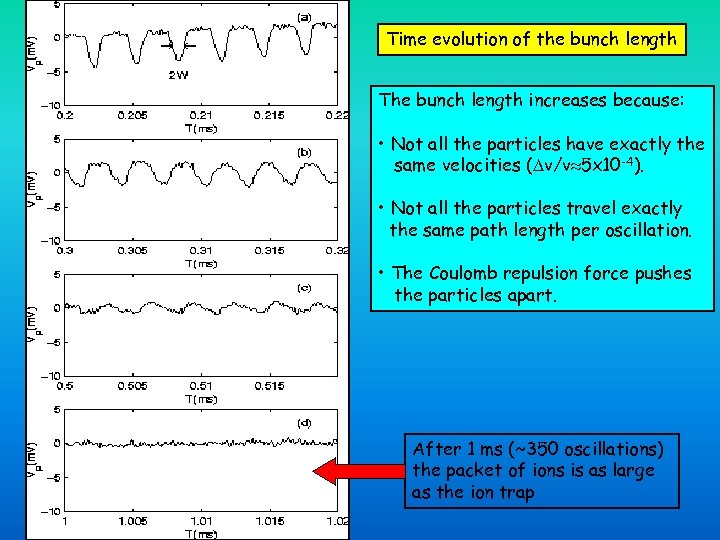
Time evolution of the bunch length The bunch length increases because: • Not all the particles have exactly the same velocities ( v/v 5 x 10 -4). • Not all the particles travel exactly the same path length per oscillation. • The Coulomb repulsion force pushes the particles apart. After 1 ms (~350 oscillations) the packet of ions is as large as the ion trap

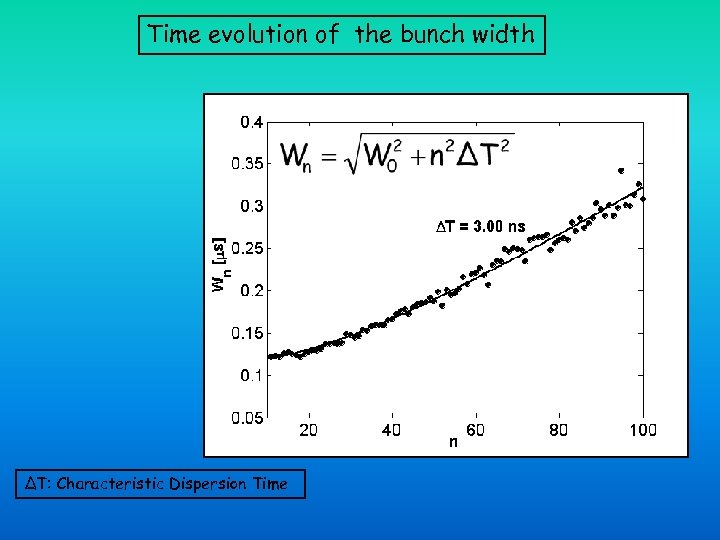
Time evolution of the bunch width ΔT: Characteristic Dispersion Time

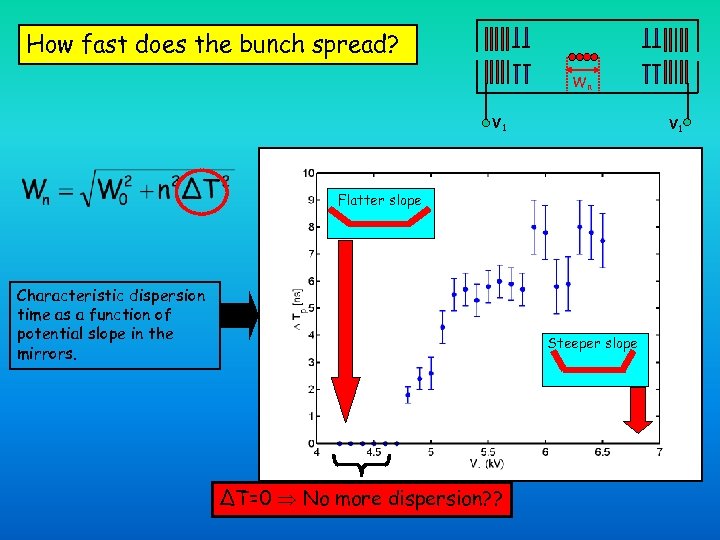
How fast does the bunch spread? Wn V 1 Flatter slope Characteristic dispersion time as a function of potential slope in the mirrors. Steeper slope ΔT=0 No more dispersion? ?

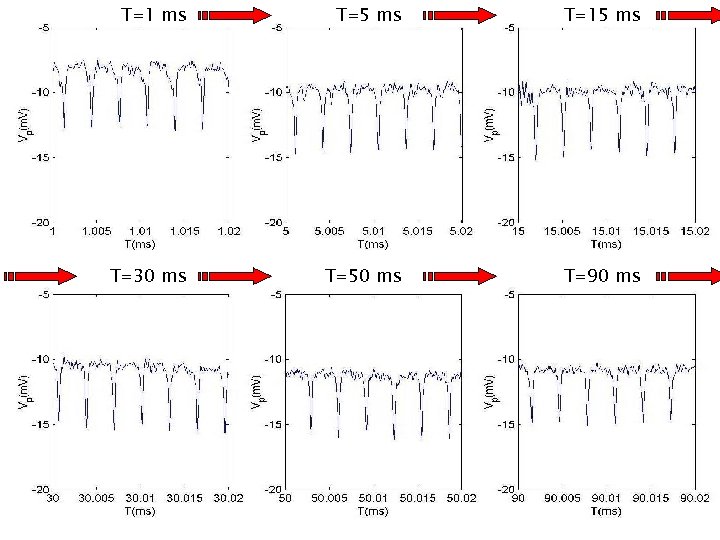
T=1 ms T=5 ms T=15 ms T=30 ms T=50 ms T=90 ms

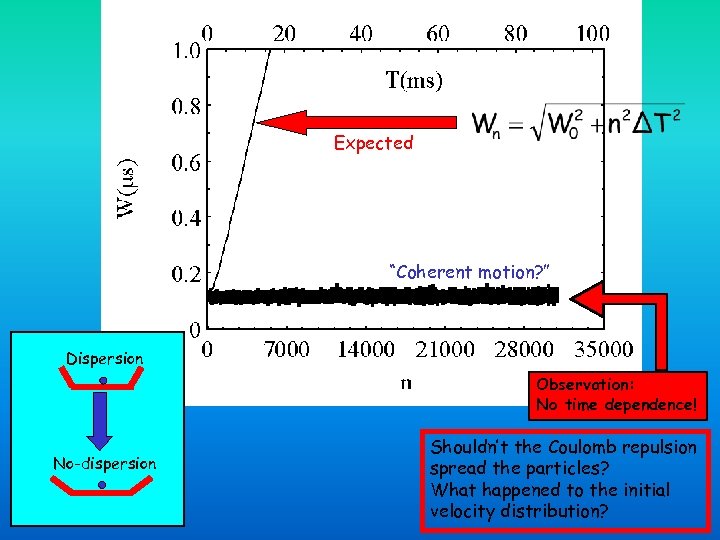
Expected “Coherent motion? ” Dispersion Observation: No time dependence! No-dispersion Shouldn’t the Coulomb repulsion spread the particles? What happened to the initial velocity distribution?

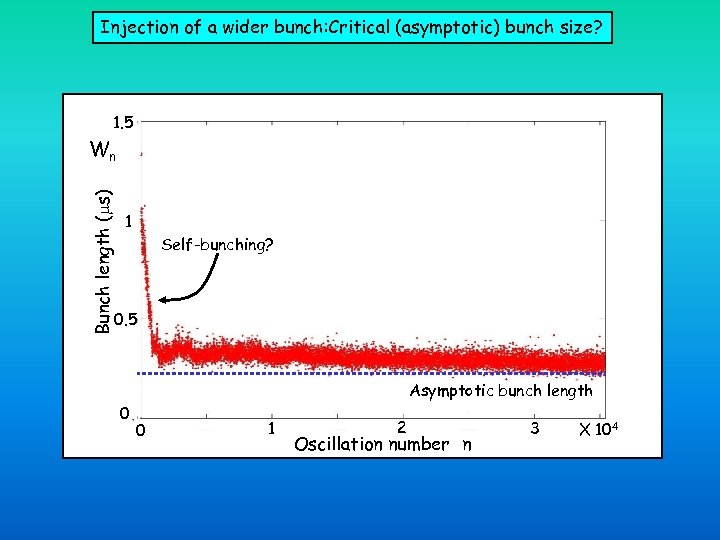
Injection of a wider bunch: Critical (asymptotic) bunch size? 1. 5 Bunch length ( s) Wn 1 Self-bunching? 0. 5 Asymptotic bunch length 0 0 1 2 Oscillation number n 3 X 104

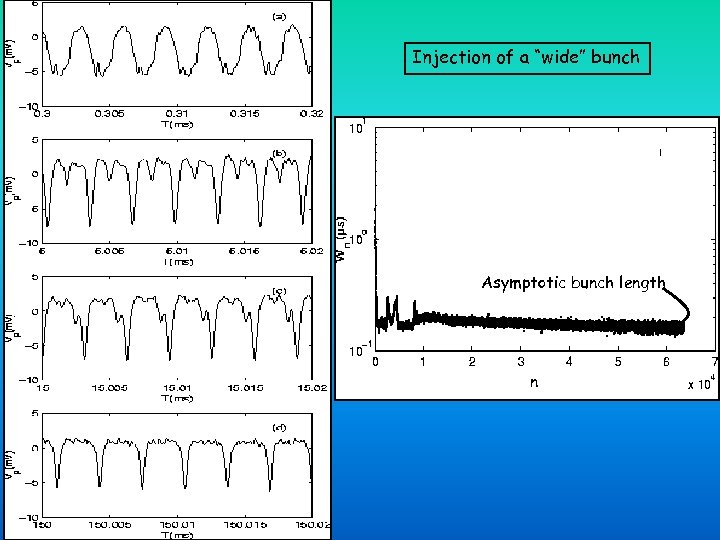
Injection of a “wide” bunch Asymptotic bunch length n

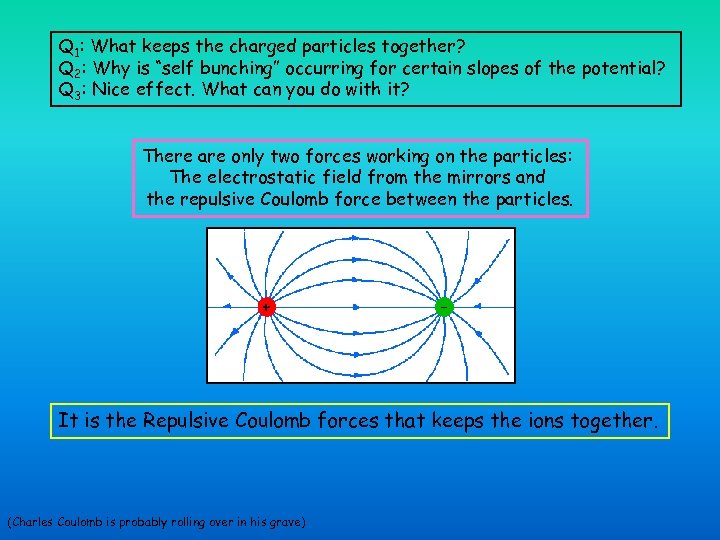
Q 1: What keeps the charged particles together? Q 2: Why is “self bunching” occurring for certain slopes of the potential? Q 3: Nice effect. What can you do with it? There are only two forces working on the particles: The electrostatic field from the mirrors and the repulsive Coulomb force between the particles. + - It is the Repulsive Coulomb forces that keeps the ions together. (Charles Coulomb is probably rolling over in his grave)

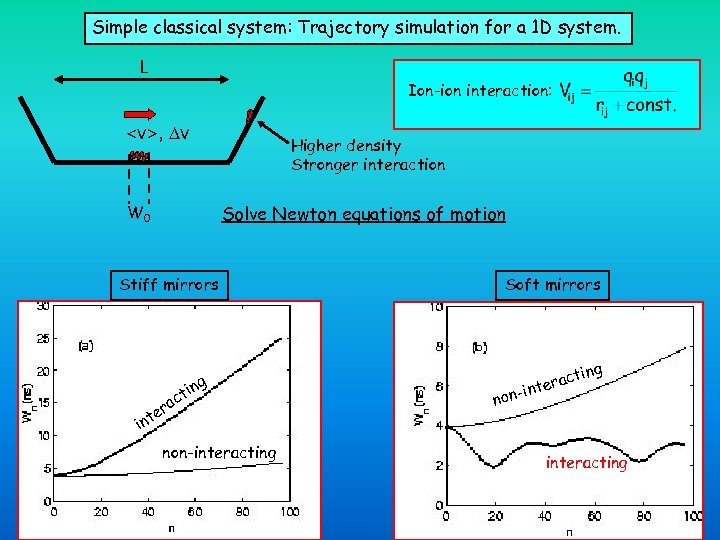
Simple classical system: Trajectory simulation for a 1 D system. L Ion-ion interaction: <v>, v Higher density Stronger interaction Solve Newton equations of motion W 0 Stiff mirrors ct a er int ing non-interacting Soft mirrors ng acti r -inte non interacting “Bound”!

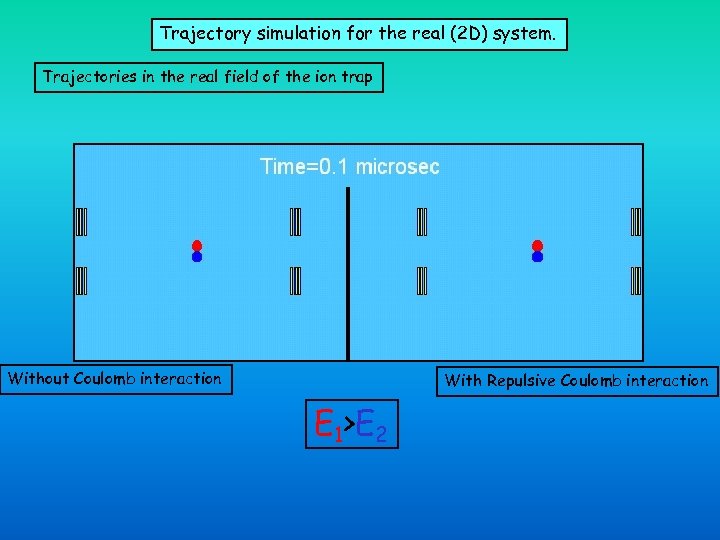
Trajectory simulation for the real (2 D) system. Trajectories in the real field of the ion trap Without Coulomb interaction With Repulsive Coulomb interaction E 1>E 2

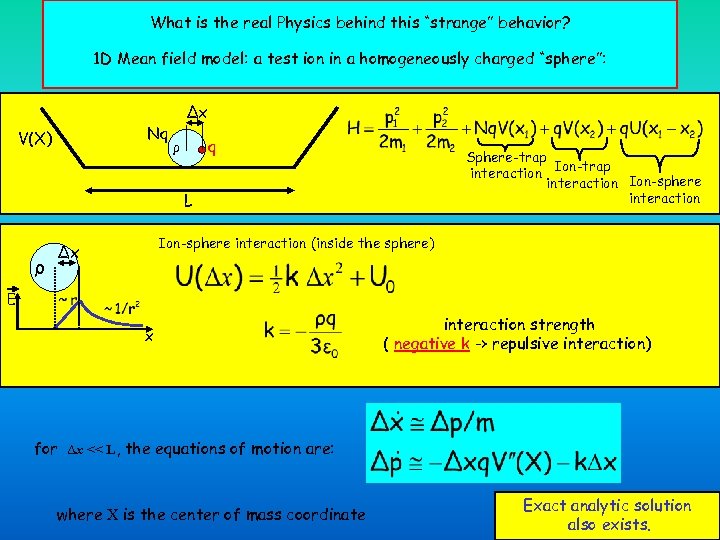
What is the real Physics behind this “strange” behavior? 1 D Mean field model: a test ion in a homogeneously charged “sphere”: Nq V(X) Δx q ρ Sphere-trap Ion-trap interaction Ion-sphere interaction L ρ Ion-sphere interaction (inside the sphere) Δx E x interaction strength ( negative k -> repulsive interaction) for Δx << L, the equations of motion are: where X is the center of mass coordinate Exact analytic solution also exists.

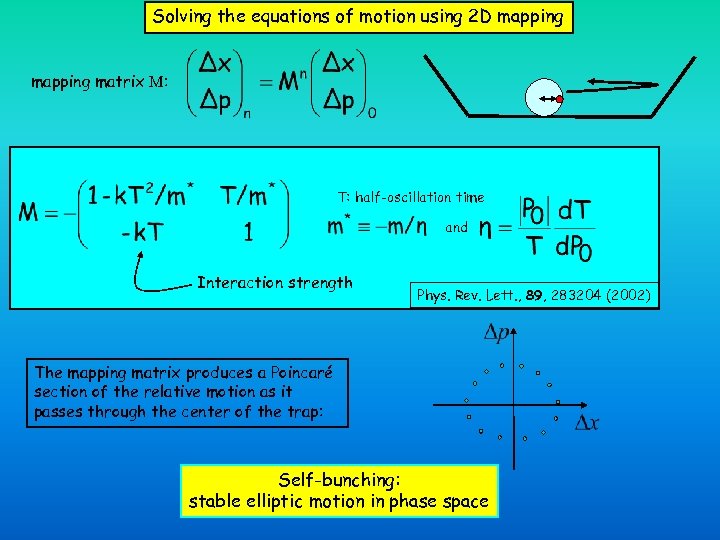
Solving the equations of motion using 2 D mapping matrix M: T: half-oscillation time and Interaction strength Phys. Rev. Lett. , 89, 283204 (2002) The mapping matrix produces a Poincaré section of the relative motion as it passes through the center of the trap: Self-bunching: stable elliptic motion in phase space

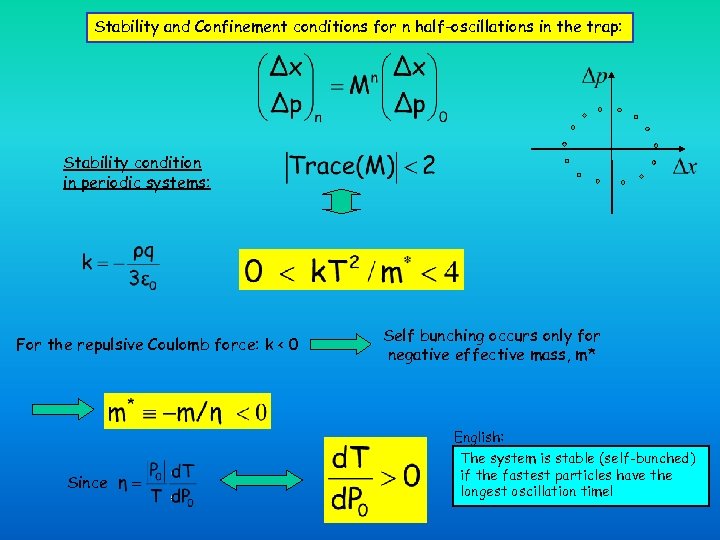
Stability and Confinement conditions for n half-oscillations in the trap: Stability condition in periodic systems: For the repulsive Coulomb force: k < 0 Since Self bunching occurs only for negative effective mass, m* English: The system is stable (self-bunched) if the fastest particles have the longest oscillation time!

Synchronization occurs only if d. T/dp>0 Physics 001 Oscillation period in a 1 D potential well: m, p S=“slope” L “Weak” slope yields to self-bunching!

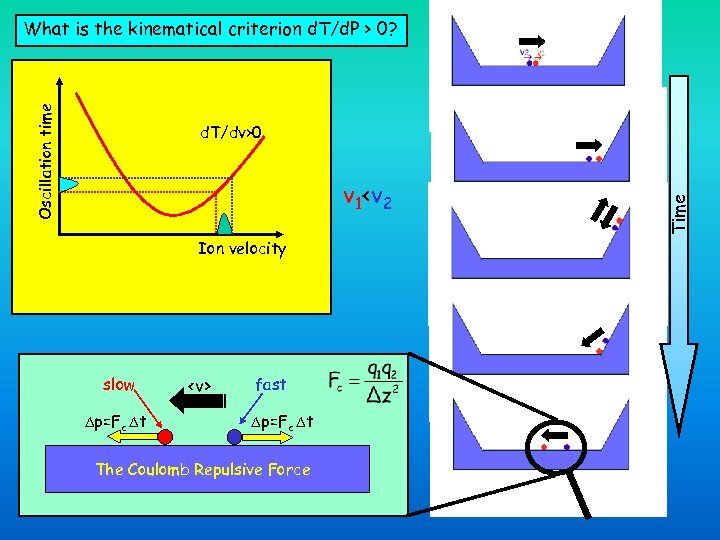
Oscillation time What is the kinematical criterion d. T/d. P > 0? v 1<v 2 Ion velocity slow p=Fc t <v> fast p=Fc t The Coulomb Repulsive Force Time d. T/dv>0

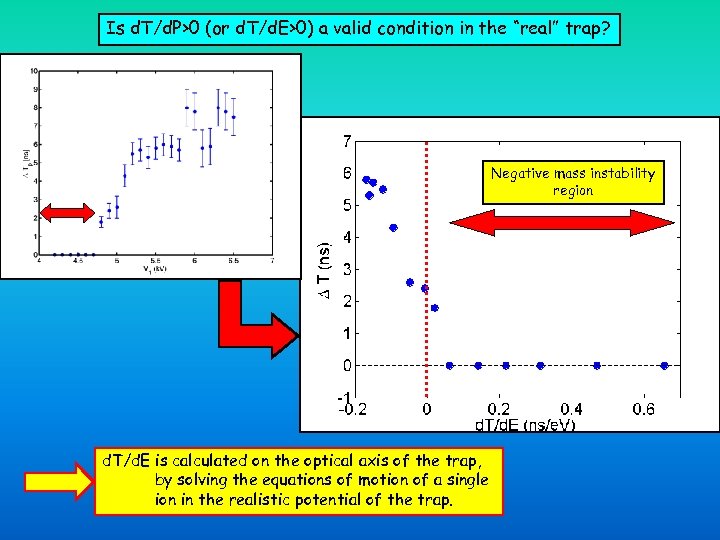
Is d. T/d. P>0 (or d. T/d. E>0) a valid condition in the “real” trap? Negative mass instability region d. T/d. E is calculated on the optical axis of the trap, by solving the equations of motion of a single ion in the realistic potential of the trap.

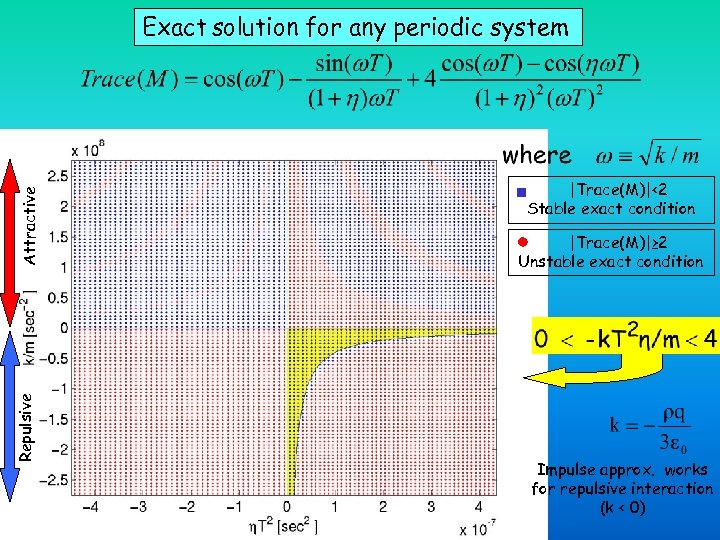
Repulsive Attractive Exact solution for any periodic system |Trace(M)|<2 Stable exact condition |Trace(M)|≥ 2 Unstable exact condition Impulse approx. works for repulsive interaction (k < 0)

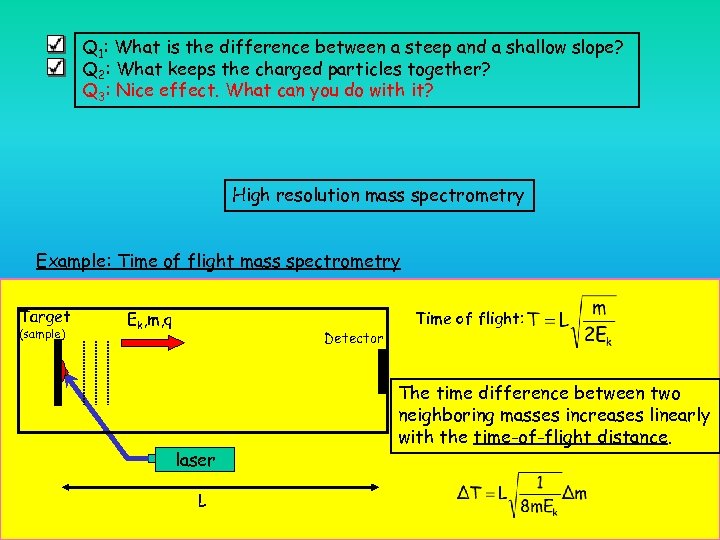
Q 1: What is the difference between a steep and a shallow slope? Q 2: What keeps the charged particles together? Q 3: Nice effect. What can you do with it? High resolution mass spectrometry Example: Time of flight mass spectrometry Target (sample) Ek, m, q Detector laser L Time of flight: The time difference between two neighboring masses increases linearly with the time-of-flight distance.

The Fourier Time of Flight Mass Spectrometer Camera MALDI Ion Source Laser Ion trap MCP detector

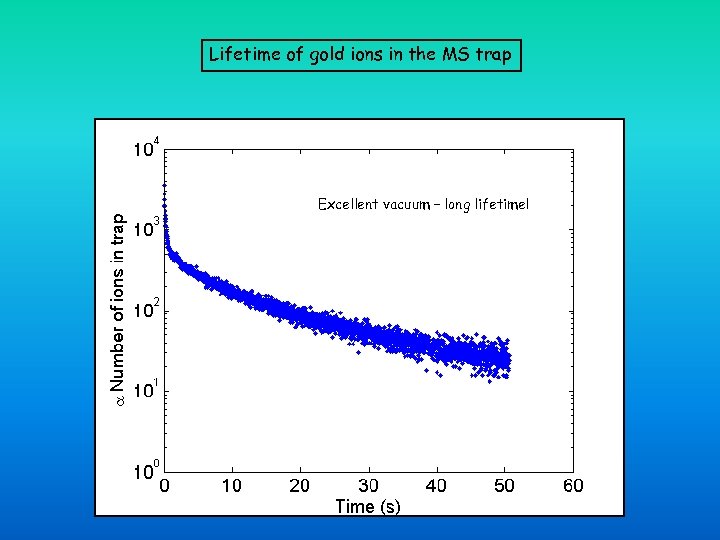
Lifetime of gold ions in the MS trap Excellent vacuum – long lifetime!

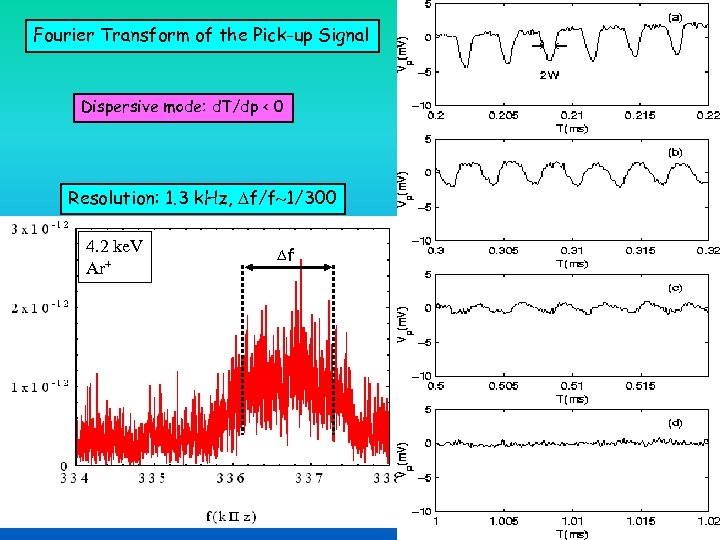
Fourier Transform of the Pick-up Signal Dispersive mode: d. T/dp < 0 Resolution: 1. 3 k. Hz, f/f 1/300 4. 2 ke. V Ar+ f .

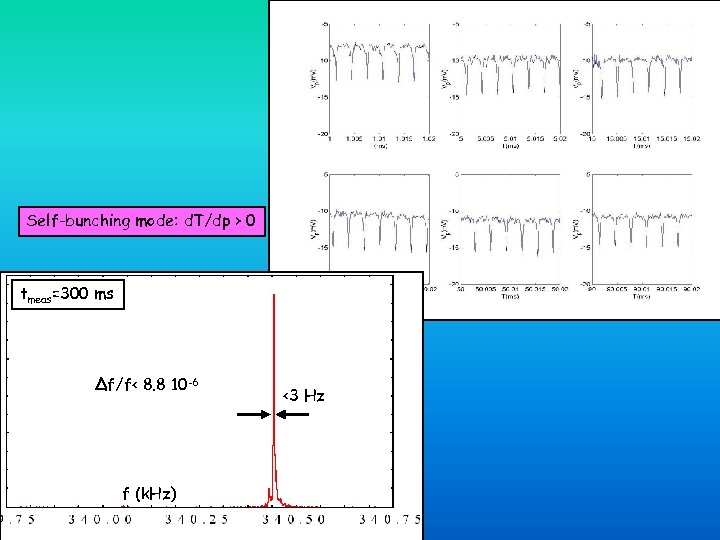
Self-bunching mode: d. T/dp > 0 tmeas=300 ms Δf/f< 8. 8 10 -6 f (k. Hz) <3 Hz

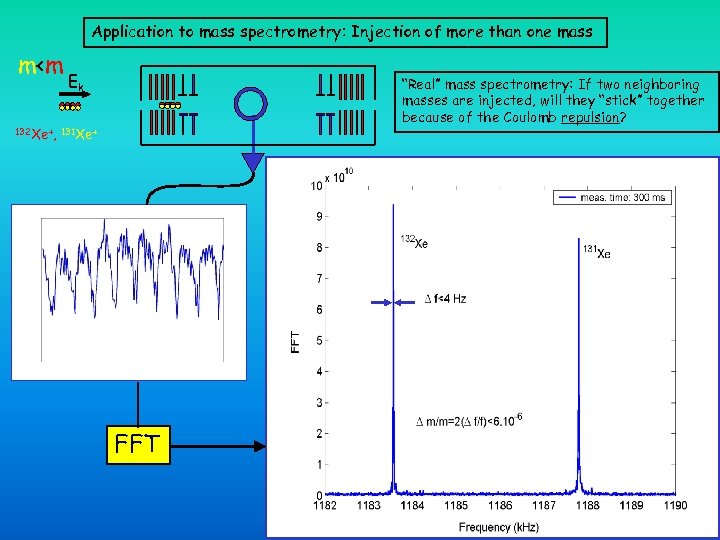
Application to mass spectrometry: Injection of more than one mass m<m Ek “Real” mass spectrometry: If two neighboring masses are injected, will they “stick” together because of the Coulomb repulsion? 132 Xe+, 131 Xe+ FFT

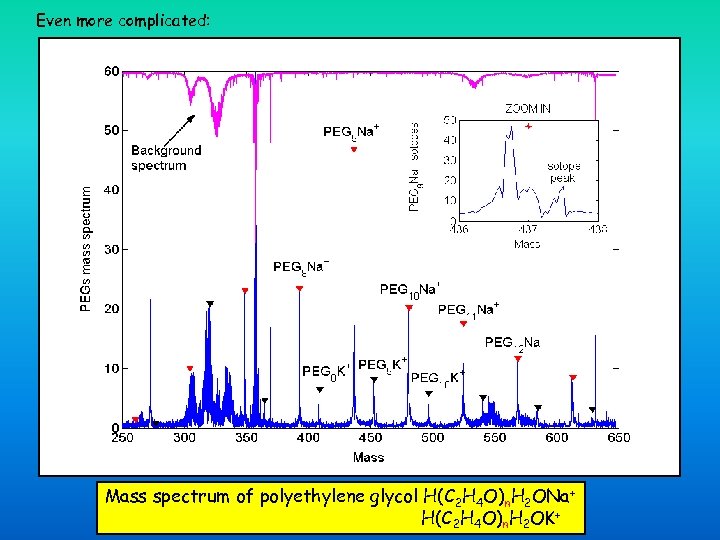
Even more complicated: Mass spectrum of polyethylene glycol H(C 2 H 4 O)n. H 2 ONa+ H(C 2 H 4 O)n. H 2 OK+

Future outlook: • Complete theoretical model, including critical density and bunch size • Peak coalescence • Can this really be used as a mass spectrometer? • Study of “mode” locking • Transverse “mode” measurement • Stochastic cooling • Transverse resistive cooling • Trap geometry • Atomic and Molecular Physics Combined Ion trap and Electron Target