Dynamics-Based Topology Identification of Complex Networks Zhigang Zheng

Dynamics-Based Topology Identification of Complex Networks Zhigang Zheng Department of Physics Beijing Normal University CCAST, Beijing, 2009. 12

Collaborators 杨浦博士 p 王群博士后 p p Prof. Choi-heng Lai (Temasek Lab, NUS, Singapore)

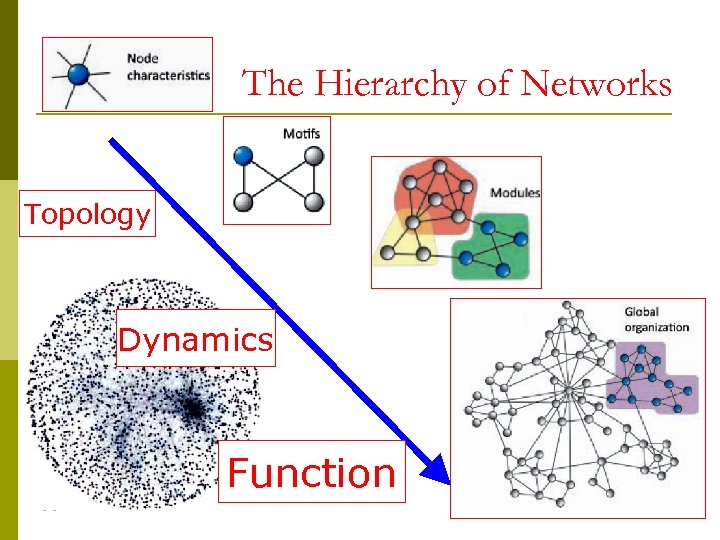
The Hierarchy of Networks Topology Dynamics Function

Topology effects on Dynamics There have been numerous and extensive investigations and reviews p Synchronizations p Spreading, Propagations, transport, …… p Swarming, flocking p

p p Recent Reviews: Complex networks: Structure and dynamics, Phys. Rep. 424, 175 (2006). Dynamics on Complex Networks and Applications (Special issue), Physica D 224 (2006). Synchronization in complex networks, Phys. Rep. 469, 93 (2008).

Topology VS Dynamics: Scale connections p In fact, the topology effect on collective dynamics is far from being clearly understood.

Also In ecology and others……

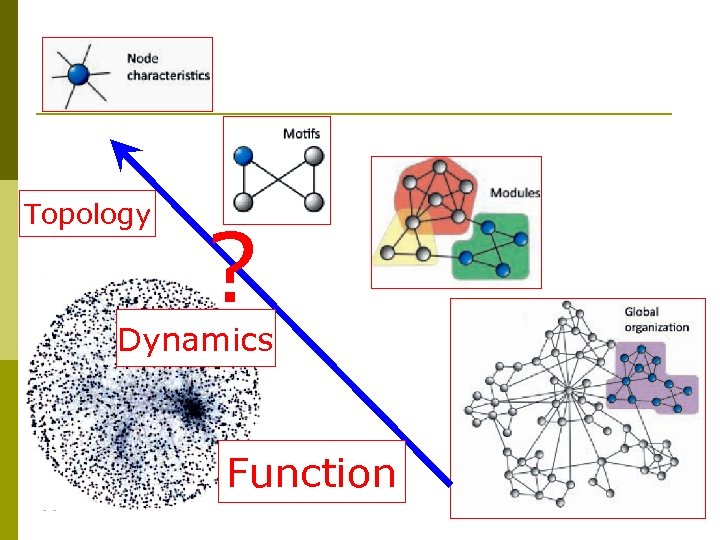
Topology ? Dynamics Function

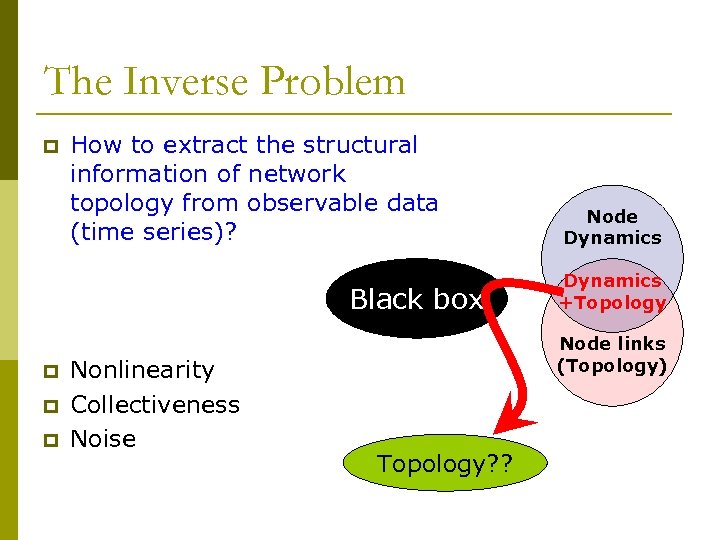
The Inverse Problem p How to extract the structural information of network topology from observable data (time series)? Black box p p p Nonlinearity Collectiveness Noise Node Dynamics +Topology Node links (Topology) Topology? ?

1. Identification of Microscopic Structures p Complete information of the network topology based on dynamics (adjacent matrix) Approaches: p Adaptive feedback p Perturbation and response dynamics p Phase dynamics p

1. 1 p 1. 2. 3. 4. 5. Adaptive feedback approach: References: D. Yu, M. Righero, and L. Kocarev, PRL 97, 188701(2006). X. Wu, Physica A 387, 997 (2008). F. Sorrentino and E. Ott, PRE 79, 016201 (2009). Z. Wu and X. Fu, CPL 26, 070201 (2009). L. Chen, J. Lu, and C. K. Tse, IEEE TRANS. CIR. & SYS. II 56, 310 (2009).

D. Yu, M. Righero, and L. Kocarev, PRL 97, 188701(2006).

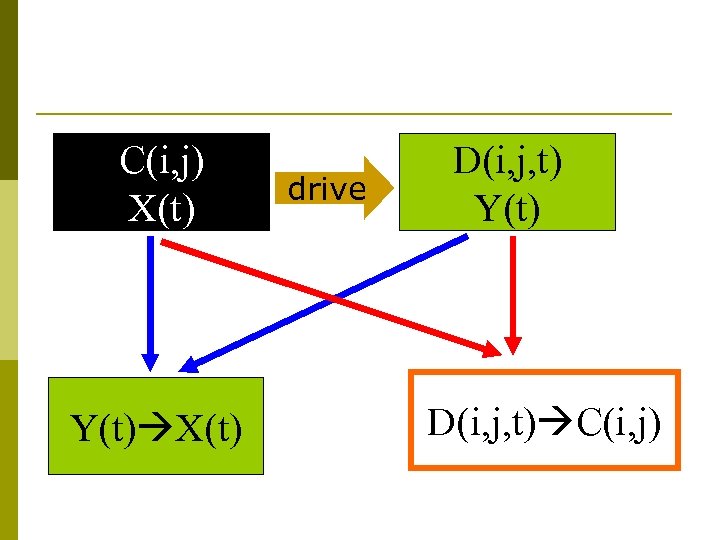
C(i, j) X(t) Y(t) X(t) drive D(i, j, t) Y(t) D(i, j, t) C(i, j)

Shortcomings: p Depending on the node dynamics and knowledge of interactions p p Failure in the presence of synchronization (partial or global)

p 1. 2 Perturbation and Response Dynamics Approach: p References: M. Timme, PRL 98, 224101 (2007). M. Timme, EPL 76, 367 (2006). D. Yu, L. Fortuna, and F. Liu, Chaos 18, 043101 (2008). D. Yu and U. Parlitz, EPL 81, 48007 (2008). 1. 2. 3. 4.

p Kuramoto with external input I: p Phase-locked state: p Linear response p Difference p Taylor expansion

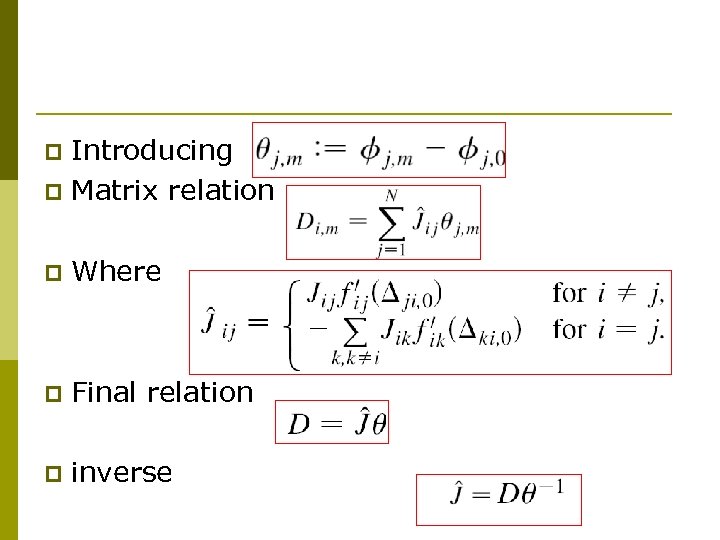
Introducing p Matrix relation p p Where p Final relation p inverse

p 1. 3 Phase Dynamics Approach: p References: A. Bahraminasab, F. Ghasemi, A. Stefanovska, P. V. E. Mc. Clintock, and H. Kantz, PRL 100, 084101 (2008). D. A. Smirnov and B. P. Bezruchko, PRE 79, 046204 (2009). 1. 2.

2. Identification of Mesoscopic Structures p Exact exploration of some topology properties based on Dynamics (motif, modules, community, et al. ) p References: S. Boccaletti, M. Ivanchenko, V. Latora, A. Pluchino, and A. Rapisarda, PRE 75, 045102(R) (2007). Y. Hu, M. Li, P. Zhang, Y. Fan, and Z. Di, PRE 78, 016115 (2008). V. Gudkov, V. Montealegre, S. Nussinov, and Z. Nussinov, PRE 78, 016113 (2008). 1. 2. 3.

3. Identification of Macroscopic Structures p A statistical estimation of network topology (A Complex-Network Approach) References: p S. Bu and I. Jiang, EPL 82, 68001 (2008). p

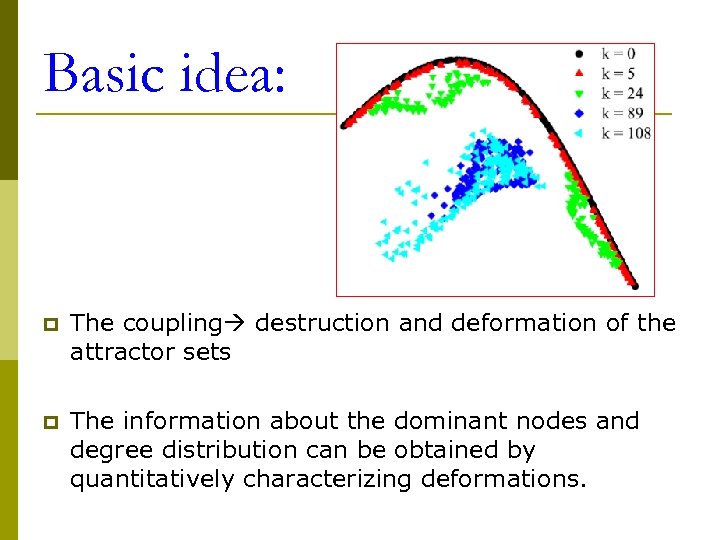
Basic idea: p The coupling destruction and deformation of the attractor sets p The information about the dominant nodes and degree distribution can be obtained by quantitatively characterizing deformations.

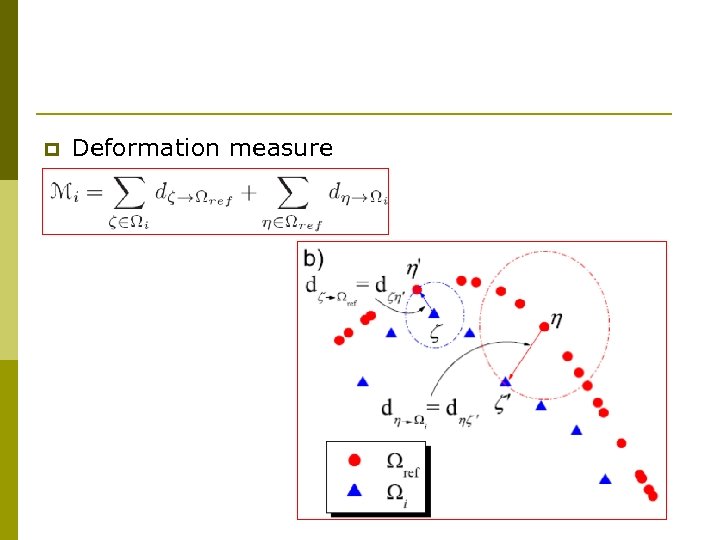
p Deformation measure

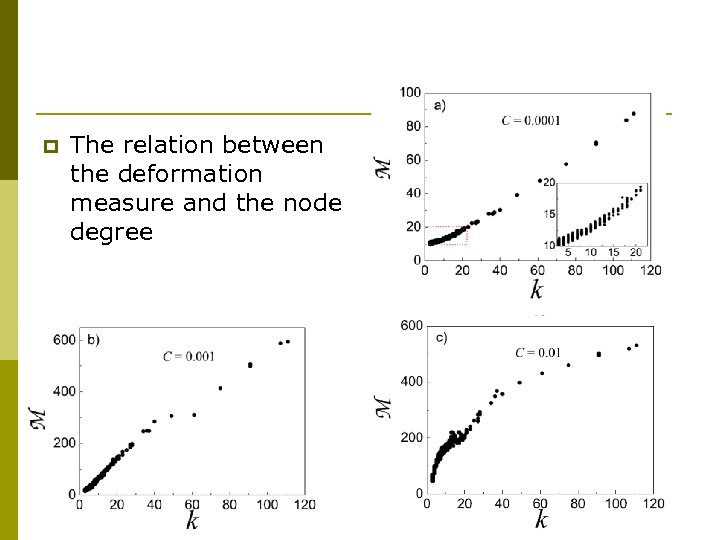
p The relation between the deformation measure and the node degree

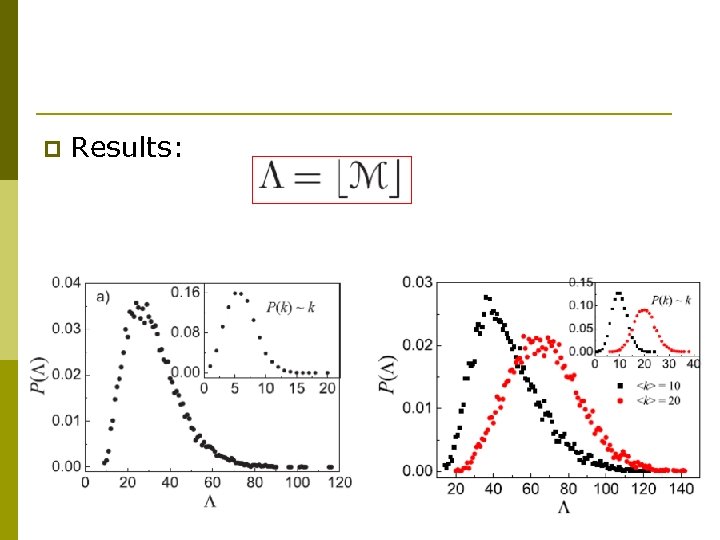
p Results:

p Shortcomings: Time-consuming p Not applicable for all chaotic dynamics p Nonlinear dependence of M on k p Failure for non-chaotic data p Failure for synchronous data p

Our Recent Works: p Identification of network topology in the presence of synchronization p Estimating statistical properties of network topology (under progress)

p Dynamical Network p adaptive-feedback Identifier p Lipschitz condition

p Evolution of the Error p Lyapunov function p One can prove

p In the long-term limit: p Linear independence condition p In the presence of synchronization

Example: Lorenz node S: coupling strength

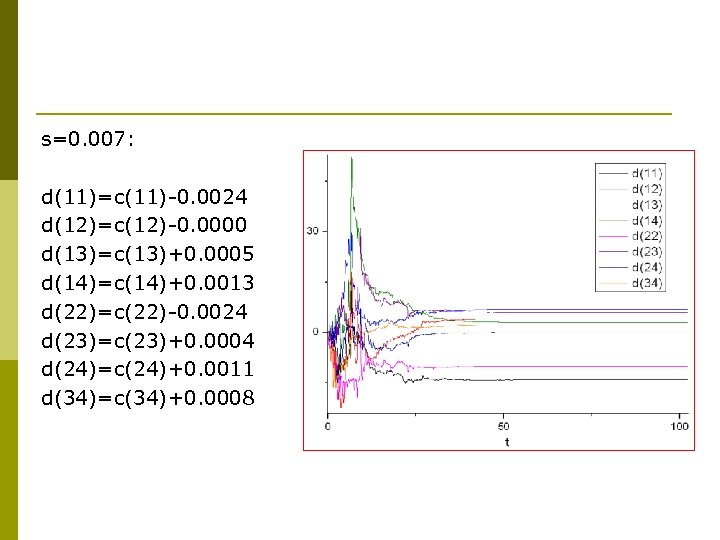
s=0. 007: d(11)=c(11)-0. 0024 d(12)=c(12)-0. 0000 d(13)=c(13)+0. 0005 d(14)=c(14)+0. 0013 d(22)=c(22)-0. 0024 d(23)=c(23)+0. 0004 d(24)=c(24)+0. 0011 d(34)=c(34)+0. 0008

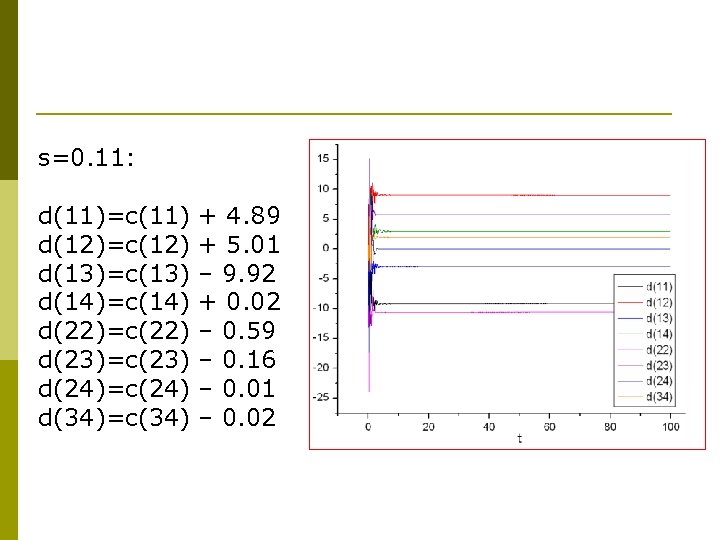
s=0. 11: d(11)=c(11) d(12)=c(12) d(13)=c(13) d(14)=c(14) d(22)=c(22) d(23)=c(23) d(24)=c(24) d(34)=c(34) + 4. 89 + 5. 01 – 9. 92 + 0. 02 – 0. 59 – 0. 16 – 0. 01 – 0. 02

p Synchronization is the obstacle to identification of network topology Question: p How to identify the network topology in the presence of synchronization? p Most Important: asynchronous information is important p Further—Ways to desynchronize…… p

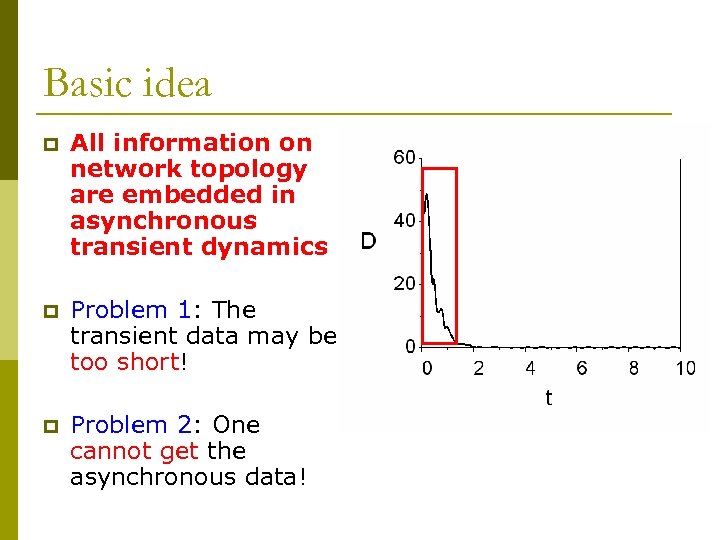
Basic idea p All information on network topology are embedded in asynchronous transient dynamics p Problem 1: The transient data may be too short! p Problem 2: One cannot get the asynchronous data!

p Solution 1: The asynchronous data (the transient segment) can be used as a repeat (periodic) drive p Solution 2: One can perturb the system via an external short-term stimuli (e. g. , a shock) to drive the system tentatively away from synchrony and to get an asynchronous segment

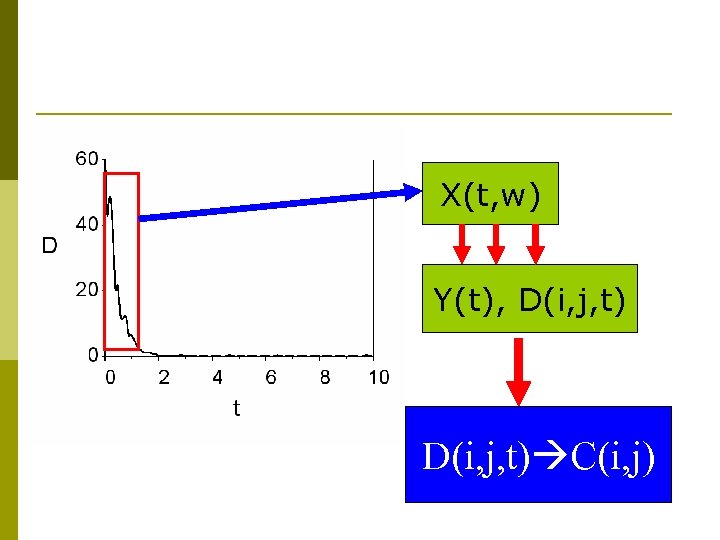
X(t, w) Y(t), D(i, j, t) C(i, j)

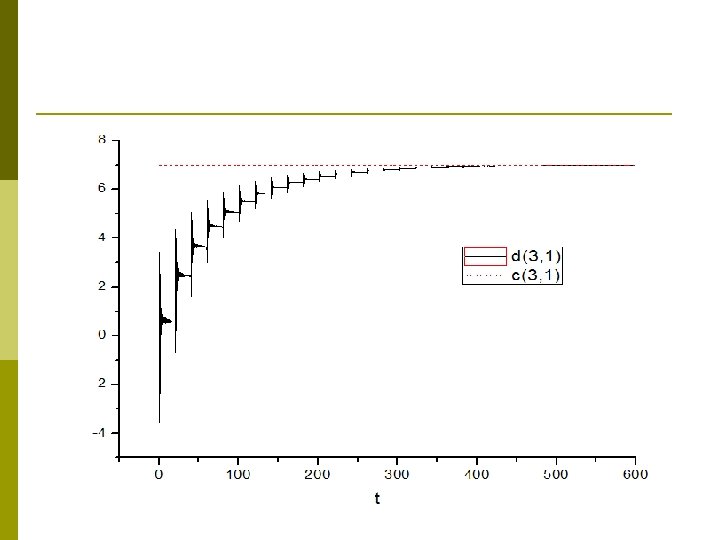
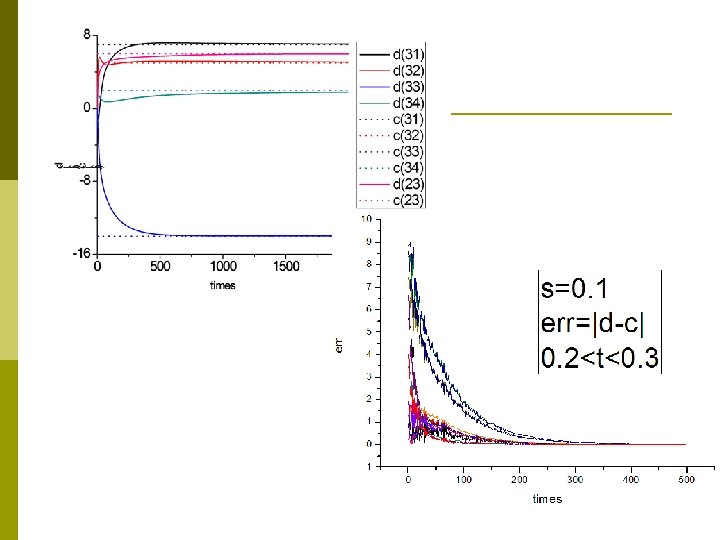
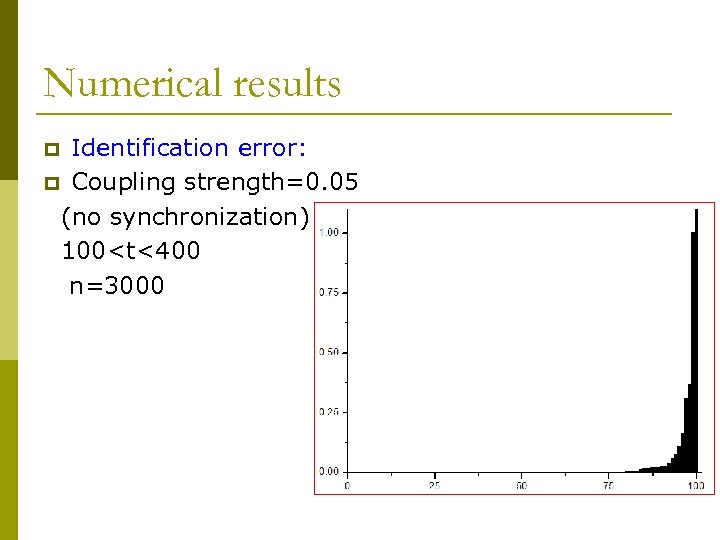
Numerical results Identification error: p Coupling strength=0. 05 (no synchronization) 100<t<400 n=3000 p

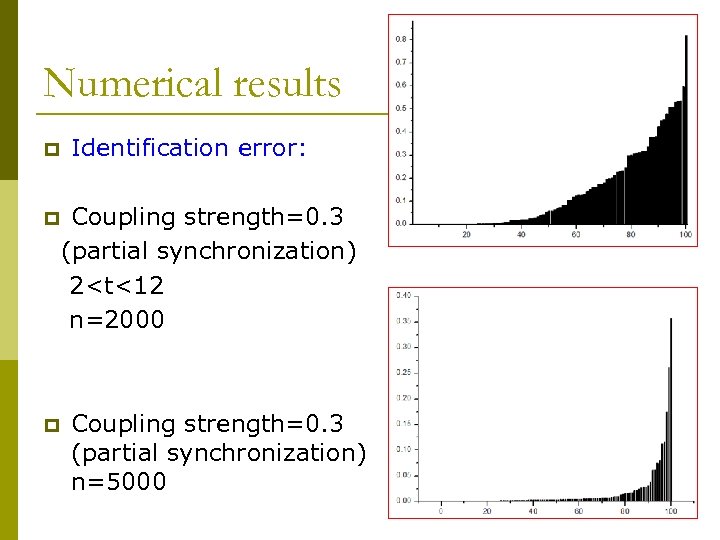
Numerical results p p p Identification error: Coupling strength=0. 3 (partial synchronization) 2<t<12 n=2000 Coupling strength=0. 3 (partial synchronization) n=5000

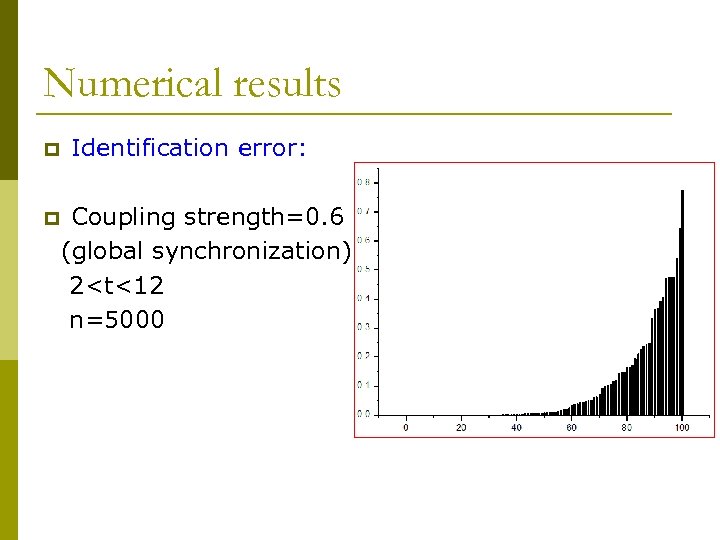
Numerical results p p Identification error: Coupling strength=0. 6 (global synchronization) 2<t<12 n=5000

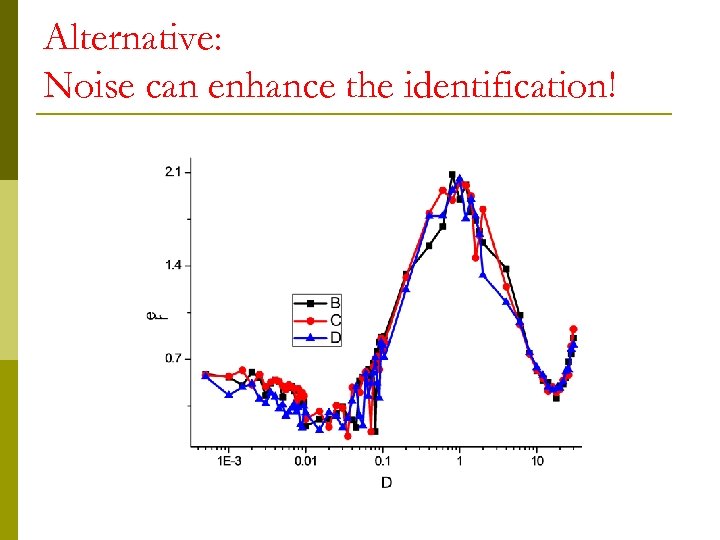
Alternative: Noise can enhance the identification!

Still going on…… p Identification of the network structure based on output data (dynamics) is a very important issue in both applications and theoretical understanding p Topology estimations in three levels are all crucial (Currently, meso-, macro-, are much more lacking, can we find some dynamics based indices to model topological properties? ) p Still far from practical applications

My permanent address: Department of Physics Beijing Normal University Beijing 100875, CHINA Email: zgzheng@bnu. edu. cn Tel. /Fax: 86 -10 -5880 -5147