Dynamic Spectrum Management Optimization game and equilibrium Tom

Dynamic Spectrum Management: Optimization, game and equilibrium Tom Luo (Yinyu Ye) December 18, WINE 2008

Outline n n Introduction of Dynamic Spectrum Management (DSM) Social Utility Optimization Noncooperative Nash Game Competitive Spectrum Economy n n Pure exchange market Budget Allocation Channel Power Production The objective is to apply algorithmic game/equilibrium theory to solving real and challenging problems

Dynamic Spectrum Management n n Communication system n DSL, cognitive radio, cellular networks, cable TV networks, Multiple users (each has a utility function) access multiple channels/tones 2/3 allocated spectrum is not being used at any given times An efficient spectrum management scheme Dynamic Spectrum Management is needed

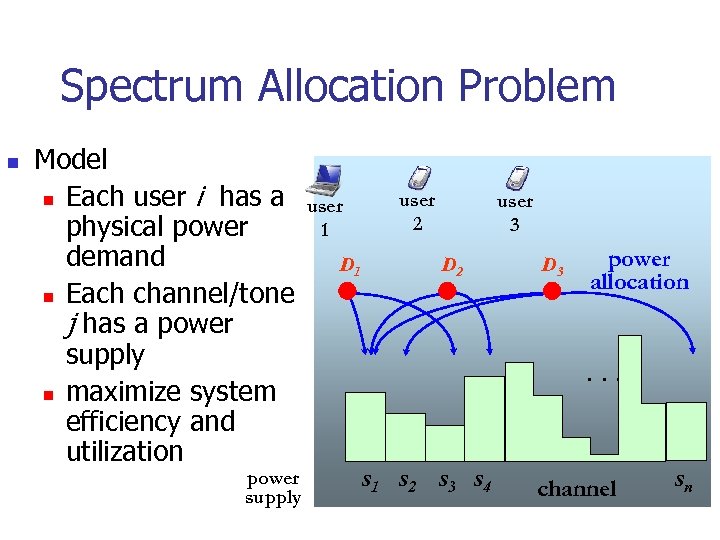
Spectrum Allocation Problem n Model n Each user i has a physical power demand n Each channel/tone j has a power supply n maximize system efficiency and utilization power supply user 1 D 1 user 2 user 3 D 2 D 3 power allocation . . . s 1 s 2 s 3 s 4 channel sn

Shannon Utility Function xij: the power allocation to user i on channel j x-bari: power allocations to all users other than i бij: the crosstalk ratio to user i on channel j aikj: the interference ratio from user k on channel j They may time varying and stochastic

Spectrum Management Models n From the optimization perspective, the dynamic spectrum management problem can be formulated as n 1. Social utility maximization n 2. Noncooperative Nash game n n May not optimize individual utilities simultaneously Generally hard to achieve May not achieve social economic efficiency 3. Competitive economy market n Price mechanism proposed to achieve social economic efficiency and individual optimality

1. Social Utility Maximization

Social Utility Maximization - a two user and two channel example user 1 1 Demand u 1= user 2 1 1 1 u 2= Channel 1 2

Difficulty of the problem n n n Even in the two user case, the problem is NPhard. No constant approximation algorithm even for one channel and multiple users. Problems under the Frequency Division Multiple Access (FMDA) policy can be solved efficiently Luo and Zhang 2007

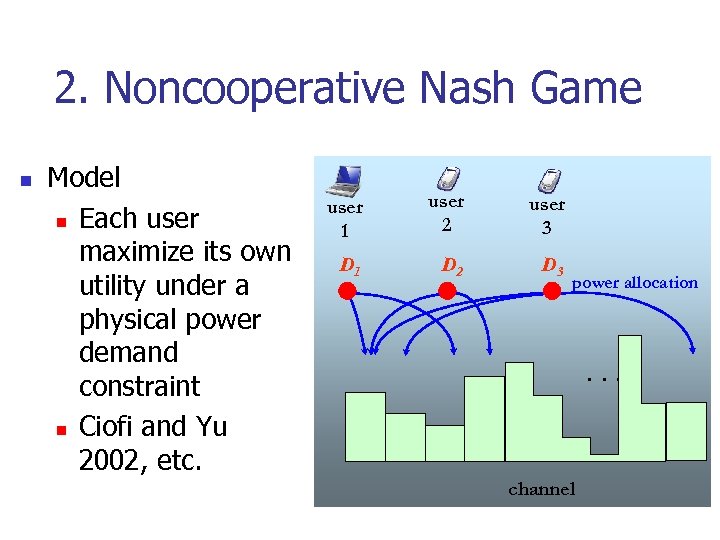
2. Noncooperative Nash Game n Model n Each user maximize its own utility under a physical power demand constraint n Ciofi and Yu 2002, etc. user 1 user 2 user 3 D 1 D 2 D 3 power allocation . . . channel

Individual rationality The basic game assumes that there is no limit on power supply for each channel. IWF: iterative water filling algorithm converges in certain cases

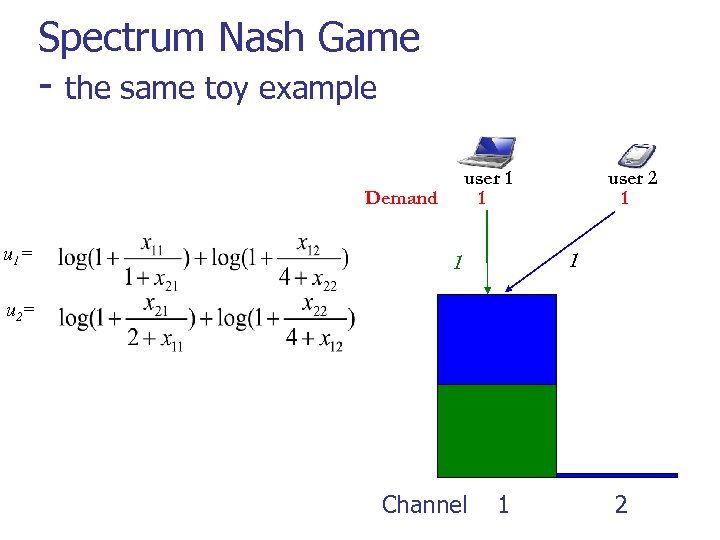
Spectrum Nash Game - the same toy example user 1 1 Demand u 1= user 2 1 1 1 u 2= Channel 1 2

Results on the problem n n No bound on ``price of anarchy’’ Can be solved as finding solution of a linear complementarity problem, so that it’s PPAD hard in general There is a FPTAS under symmetric interference condition There is a polynomial time algorithm under symmetric and strong weak interference condition Key to the proofs: the LCP matrix is symmetric Luo and Pang 2006, Xie, Armbruster, and Y 2008

3. Competitive Spectrum Market § § The problem was first formulated by Leon Walras in 1874, and later studied by Arrow, Debreu, and Fisher, also see Brainard and Scarf. Agents are divided into two categories: seller and buyer. Buyers have a budget to buy goods and maximize their individual utility functions; sellers sell their goods just for money. An equilibrium is an assignment of prices to all goods, and an allocation of goods to every buyer such that it is maximal for the buyer under the given prices and the market clears.

Market Equilibrium Condition I

Market Equilibrium Condition II Physical Constraint: The total purchase volume for good j should not exceed its available supply:

Market Equilibrium Condition III Walras Law:

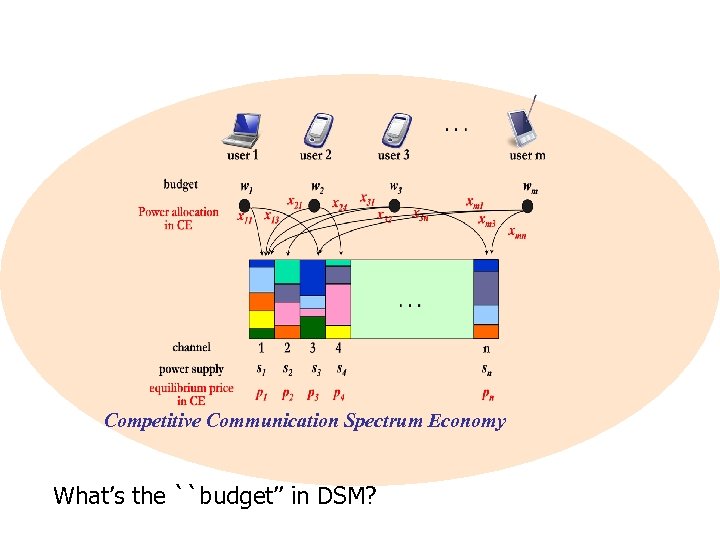
Competitive Communication Spectrum Economy What’s the ``budget’’ in DSM?

3. 1 Competitive Equilibrium in Spectrum Economy for Fixed Budget and Power Supply

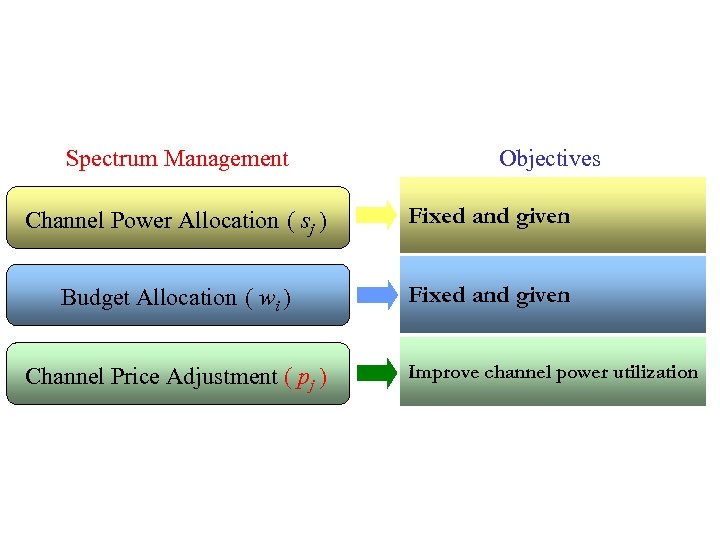
Spectrum Management Objectives Channel Power Allocation ( sj ) Fixed and given Budget Allocation ( wi ) Fixed and given Channel Price Adjustment ( pj ) Improve channel power utilization

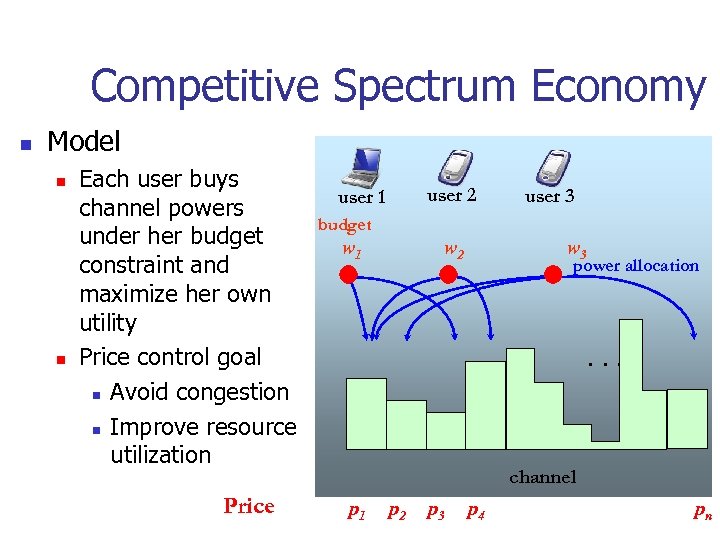
Competitive Spectrum Economy n Model n n Each user buys channel powers under her budget constraint and maximize her own utility Price control goal n Avoid congestion n Improve resource utilization Price user 2 user 1 user 3 budget w 1 w 2 w 3 power allocation . . . channel p 1 p 2 p 3 p 4 pn

Problem Formulation n m users, each has a budget wi n channels, each with power capacity sj Design variable n n n xij Power allocation for i th user in jth channel pj Price for j th channel (Nash Equilibrium: pj=1 fixed) User utility (Shannon utility function )

Competitive Equilibrium Model Theorem A competitive equilibrium always exists for the spectrum management problem Y 2007 based on the Lemma of Abstract Economy developed by Debreu 1952

Equilibrium Properties n Every channel has a price: n All power supply are allocated: n All budget are spent

Weak-Interference Market n n Weak-interference environment: the Shannon utility function of user i is In the weak-interference environment, n n An equilibrium can be computed in polynomial time. The competitive price equilibrium is unique. Moreover, if the crosstalk ratio is strictly less than 1, then the power allocation is also unique. (Y 2007)

Two methods of solving competitive equilibrium n Centralized n n Solving the equilibrium conditions Decentralized n Iterative price-adjusting

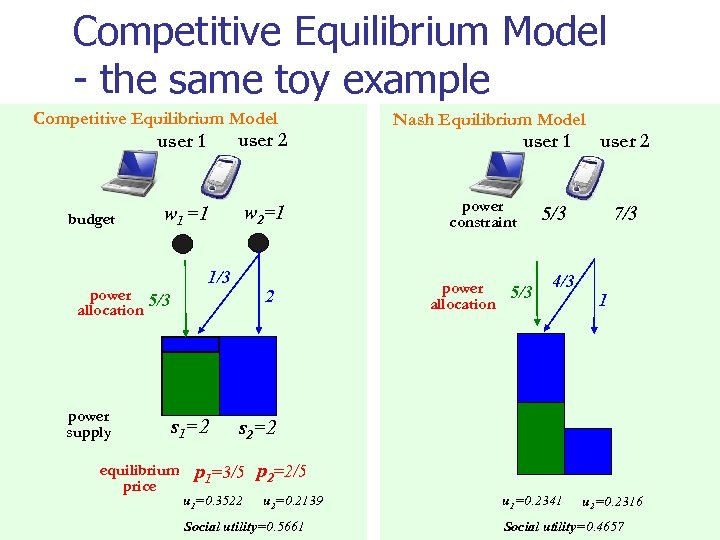
Competitive Equilibrium Model - the same toy example Competitive Equilibrium Model user 1 budget user 2 w 1 =1 w 2=1 power 5/3 allocation power supply 1/3 s 1=2 equilibrium price 2 Nash Equilibrium Model user 1 power constraint power 5/3 allocation user 2 7/3 5/3 4/3 1 s 2=2 p 1=3/5 p 2=2/5 u 1=0. 3522 u 2=0. 2139 Social utility=0. 5661 u 1=0. 2341 u 2=0. 2316 Social utility=0. 4657

Computational Results n n Compare competitive equilibrium and Nash equilibrium Evaluate the performance in n n Individual utility and Social utility In most cases, CE results in a channel allocation n n Have a higher social utility value Make more users achieve higher individual utilities

3. 2 Budget Allocation in Competitive Spectrum Economy

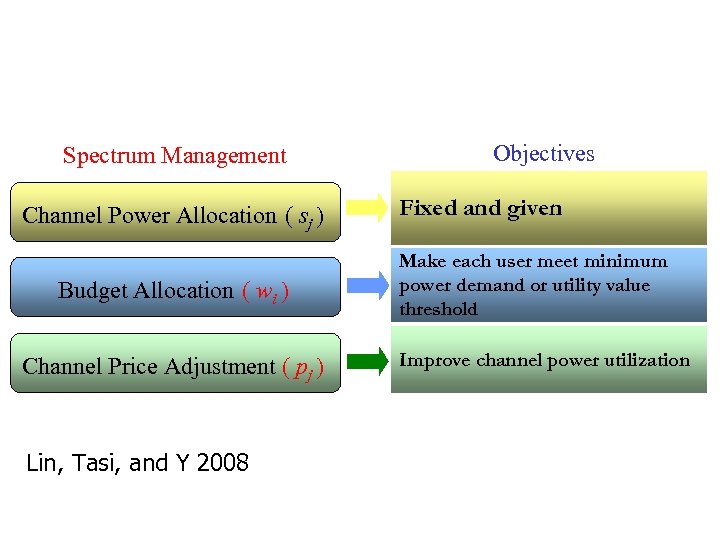
Spectrum Management Channel Power Allocation ( sj ) Budget Allocation ( wi ) Channel Price Adjustment ( pj ) Lin, Tasi, and Y 2008 Objectives Fixed and given Make each user meet minimum power demand or utility value threshold Improve channel power utilization

Budget Allocation in Competitive Spectrum Economy n Budget allocation aims to satisfy a minimum physical power demand di for each user i or n satisfy a minimum utility value ui for each user i ; e. g. , all users achieve an identical utility value n n Theorem: Such a budget equilibrium always exists.

Two methods of solving competitive equilibrium n Centralized n n Solving entire optimal conditions which may be nonconvex Decentralized n Iterative budget-adjusting

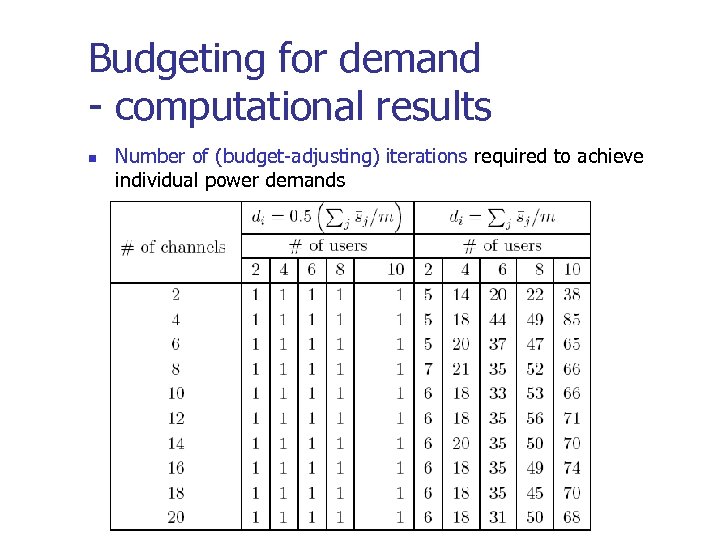
Budgeting for demand - computational results n Number of (budget-adjusting) iterations required to achieve individual power demands

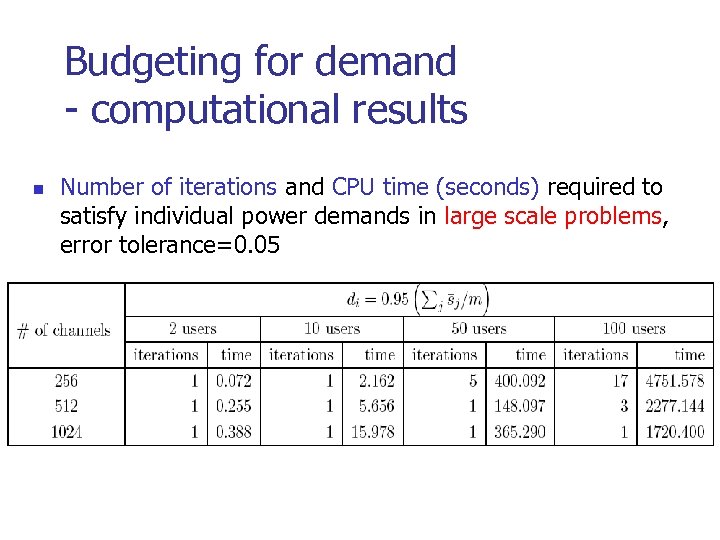
Budgeting for demand - computational results n Number of iterations and CPU time (seconds) required to satisfy individual power demands in large scale problems, error tolerance=0. 05

Budgeting for demand - CE and NE comparison results n n General cases: background noise randomly selected from (0, m], crosstalk ratio randomly selected from [0, 1] In all cases, the social utility of CE is better than that of NE.

Budgeting for demand - More CE and NE comparison results n n In special type of problems, the competitive equilibrium performs much better than the Nash equilibrium does. For instance, the channels being divided into two categories: high-quality and low-quality. (In simulations, one half of channels with background noise randomly selected from the interval (0; 0, 1] and the other half of channels with background noise randomly selected from the interval [1; m]. )

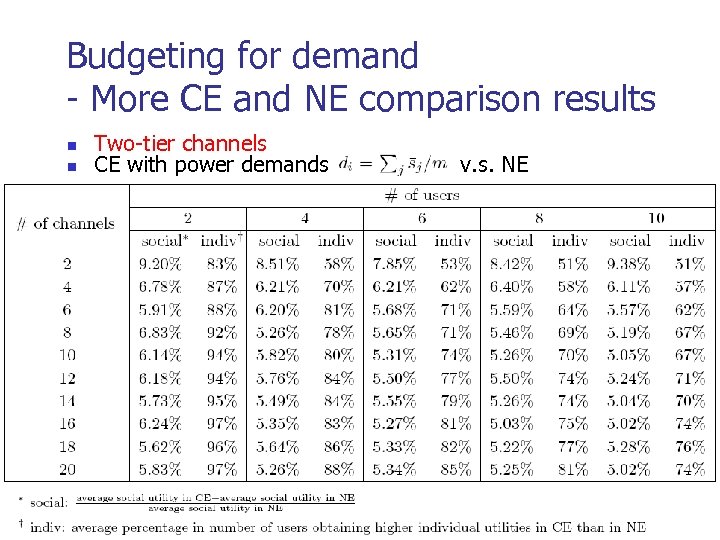
Budgeting for demand - More CE and NE comparison results n n Two-tier channels CE with power demands v. s. NE

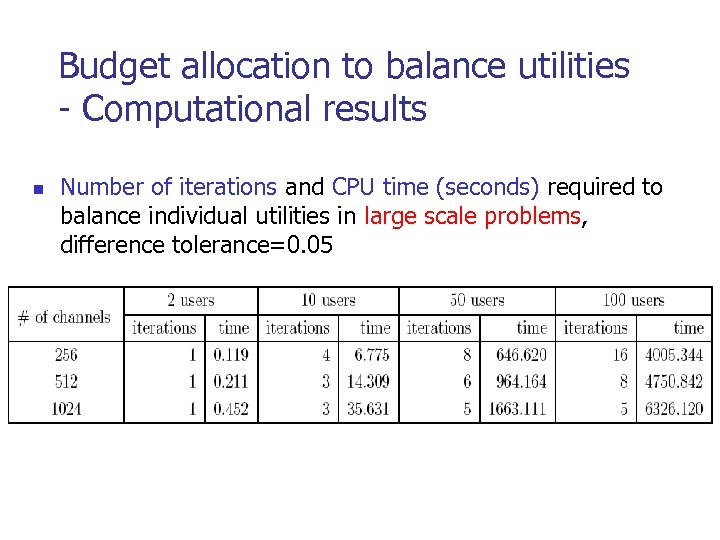
Budget allocation to balance utilities - Computational results n Number of iterations and CPU time (seconds) required to balance individual utilities in large scale problems, difference tolerance=0. 05

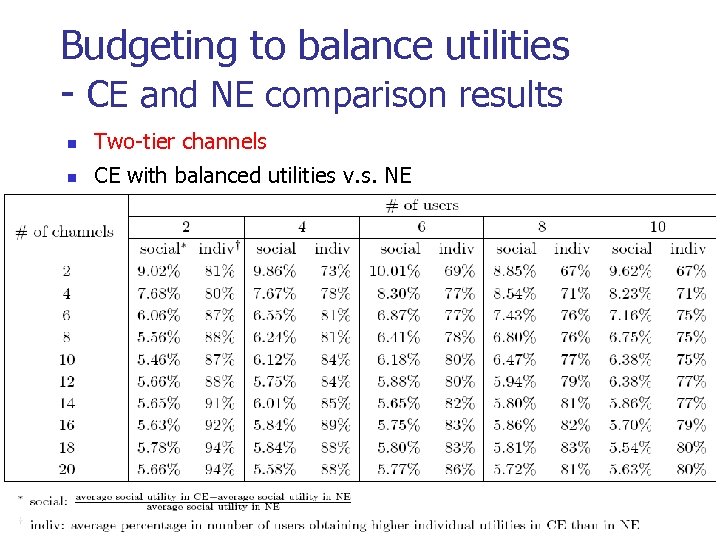
Budgeting to balance utilities - CE and NE comparison results n Two-tier channels n CE with balanced utilities v. s. NE

Comparison result summaries n Compare with NE, in most cases, CE with minimum power demands results in power allocation n n Compare with NE, in most cases, CE with balanced utilities demands results in a power allocation n n Have a higher social utility Make more users have higher individual utilities Have a smaller gap between maximal individual utility and minimal individual utility In special type of problems, for instance, two tiers of channels, CE performs much better than NE does.

3. 3 Channel Power Production in Competitive Spectrum Economy

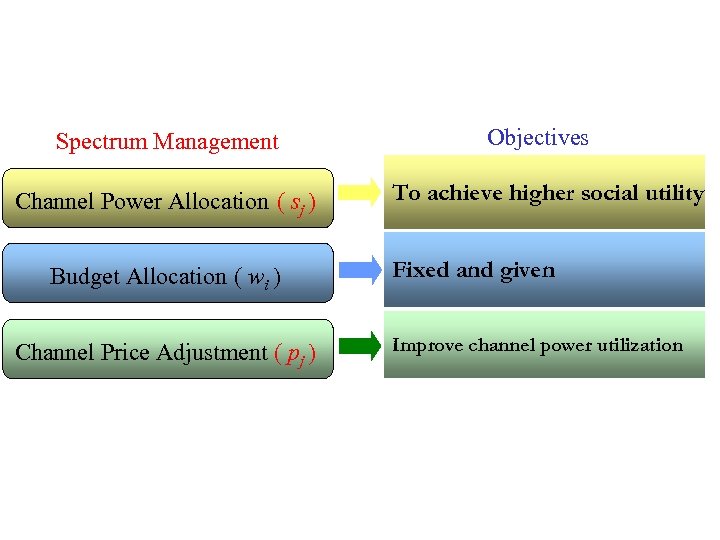
Spectrum Management Channel Power Allocation ( sj ) Budget Allocation ( wi ) Channel Price Adjustment ( pj ) Objectives To achieve higher social utility Fixed and given Improve channel power utilization

Produce power supply to increase social utility: the same toy example u 1= u 2=

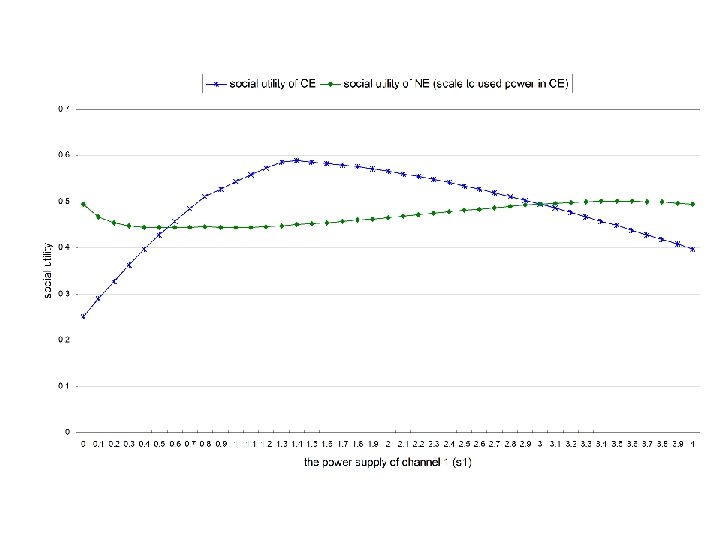
Future Work n n n How to systematically adjust channel power supply capacity to increase social utility? The convergence of the iterative variableadjusting method for general setting Real-time spectrum management vs optimal policy at top levels